基于二维信息扩散模型的收入保险费率厘定:方法与实证
2021-05-10吴海平郭凤茹李士森李晓涛任金政
吴海平 郭凤茹 李士森 李晓涛 任金政
(1.河北经贸大学 财政税务学院,石家庄 050061; 2.中国农业大学 经济管理学院,北京 100083; 3.石家庄铁路职业技术学院,石家庄 050061)
农业生产面临着产量损失和价格波动的双重风险,威胁到农户收入的稳定,降低了农户生产的积极性,给农业生产的可持续性和国民经济发展造成重大影响。为降低市场价格波动对农户收入的影响,我国从2004年开始实行以最低收购价为主的粮食价格支持政策,有效降低了农作物市场价格波动的风险,对农业生产的增长发挥了重要作用。但受国际市场粮食价格下跌和WTO“黄箱政策”约束的影响,最低收购价等政策已难以为继[1]。农业保险是世贸组织允许各国支持农业的“绿箱政策”,自2007年开始推行政策性农业保险以来,我国农业保险得到快速发展,2019年我国农业保险保费收入达680亿元,为全国1.8亿农户提供了3.6万亿元的风险保障。
我国目前的政策性农业保险以成本保险为主,主要从产量损失的角度为农业生产提供风险保障,未能有效分散价格波动造成的市场风险。鉴于此,我国开始探索农作物收入保险,2017年中央一号文件中提出要“探索建立农产品收入保险制度”,2018年财政部、农业农村部和银保监会共同印发通知,正式开展三大主粮作物的收入保险试点,2019年《关于加快农业保险高质量发展的指导意见》中明确要“防范自然灾害和市场变动双重风险,稳妥有序推进收入保险,促进农户收入稳定”。农作物收入保险在美国、加拿大等发达国家已成为农产品价格风险管理的重要手段,如2017年美国农作物收入保险保费占全部农业保险保费的比重高达81%[2]。因此,从我国政策改革方向和国外发展经验看,农作物收入保险将是未来农业保险产品的主导形态。
我国农作物收入保险处于起步阶段,准确估计收入保险的价格是其顺利推行和可持续发展的关键[3]。保费偏高会造成农户的有效需求不足,保费偏低会造成保险机构的亏损,无法长期提供有效供给。同时,精确的保费费率也是制定收入保险保费补贴政策和提高补贴资金使用效率的重要前提。但是,实际操作中需要以较长的农作物单产和价格时序数据为基础,才能建立较为稳定的统计模型,准确厘定收入保险的费率。不同于国外发达国家,我国可公开获取的农作物生产和价格数据时间较短,且研究区域越小数据量越少。因此,开展农业收入保险的一个关键问题是如何深入挖掘有限的数据信息,实现保险费率的精准厘定。本研究区别于现有研究模式,引入信息扩散方法,设计了利用信息扩散模型厘定收入保险费率的方法和步骤,以河北省玉米收入保险为例验证了此方法的可行性,有效解决了现有数据样本不足情况下的收入保险费率厘定问题。探究小样本情况下农作物收入保险费率厘定方法,有利于收入保险市场的可持续发展,为保费补贴政策的制定和农业保险的发展提供理论基础。
1 文献评述
美国早期的收入保险产品CRC(Crop revenue coverage)未考虑单产和价格数据之间的相关性,可在独立风险前提下分别分析产量和价格数据的概率分布[4],综合得到收入保险费率。后期推出的收入保险产品RA(Revenue Assurance)及IP(Income Protection)对收入保险费率的厘定提出了更高要求,农作物收入保险的费率除了取决于产量与价格的分布外,还受两者相关关系的影响,因此如何测度产量与价格的相关性就成为农作物收入保险保费厘定的核心问题之一。
目前国内外关于收入保险费率厘定的研究大都采用Copula方法,因为Copula方法能够科学合理地度量多维变量间的相依结构关系[5],且每个变量可以选择灵活的边缘分布形式[6]。国外学者Tejeda等[7]较早利用Copula方法研究了爱荷华州玉米和大豆收入保险的费率厘定问题;国内谢凤杰等[8]较早利用Copula方法研究了安徽玉米、小麦与大豆收入保险的费率厘定问题。随着我国农作物收入保险试点工作的深入,国内越来越多的学者开始关注农作物收入保险的费率厘定问题。在研究种类上,现有文献既有三大主粮作物(水稻、小麦和玉米),也有棉花和大豆等经济作物,还有花生、苹果等具有地方特色的作物,作物种类具有较为广泛的代表性。在研究方法上,一些学者采用多种方法对Copula模型进行优化,例如,采用混合Copula[9]、vine-Copula[10]等方法以得到更好的拟合效果,部分研究成果如表1所示。
从现有文献看,国内学者对农作物收入保险的费率厘定都选用了Copula方法,并形成了基本成熟的研究范式,即“数据趋势处理—确定边缘分布—选择Copula函数—蒙特卡洛模拟”等4个步骤。在确定边缘分布时,常用的方法有参数估计[6,11]和非参数核密度估计[12-13]两种方法。但这两种方法均存在一定的局限性,因为农业生产灾害和市场波动风险的发生具有极大的不确定性和易变性,准确拟合农作物收入风险的分布需要较长时间序列的历史统计资料,而我国能够公开获取的农作物单产数据和价格数据较少,属于小样本数据(从表1的数据来源可以看出,一般在30~50个样本,甚至更少),这两种估计方法容易导致估计结果的不稳定:1)参数法要先假定产量波动和价格波动服从一种或几种经典的理论分布,然后利用K-S检验法、AD检验或χ2检验法选择拟合程度最好的分布,但预先设定分布存在不合理性,并且经常出现拟合优度不高的情况[14];2)分布拟合检测时,经常遇到同时接受多种不同概率分布类型的情况,不同边缘分布的选择直接影响到Copula模型的估计和费率厘定结果;3)非参数法虽不必预先假设分布模型,但不同的核函数可能对核密度估计结果产生影响,并且就我国小样本数据的情况而言,在收入保险费率厘定中,非参数法并不比参数法更合适[15]。
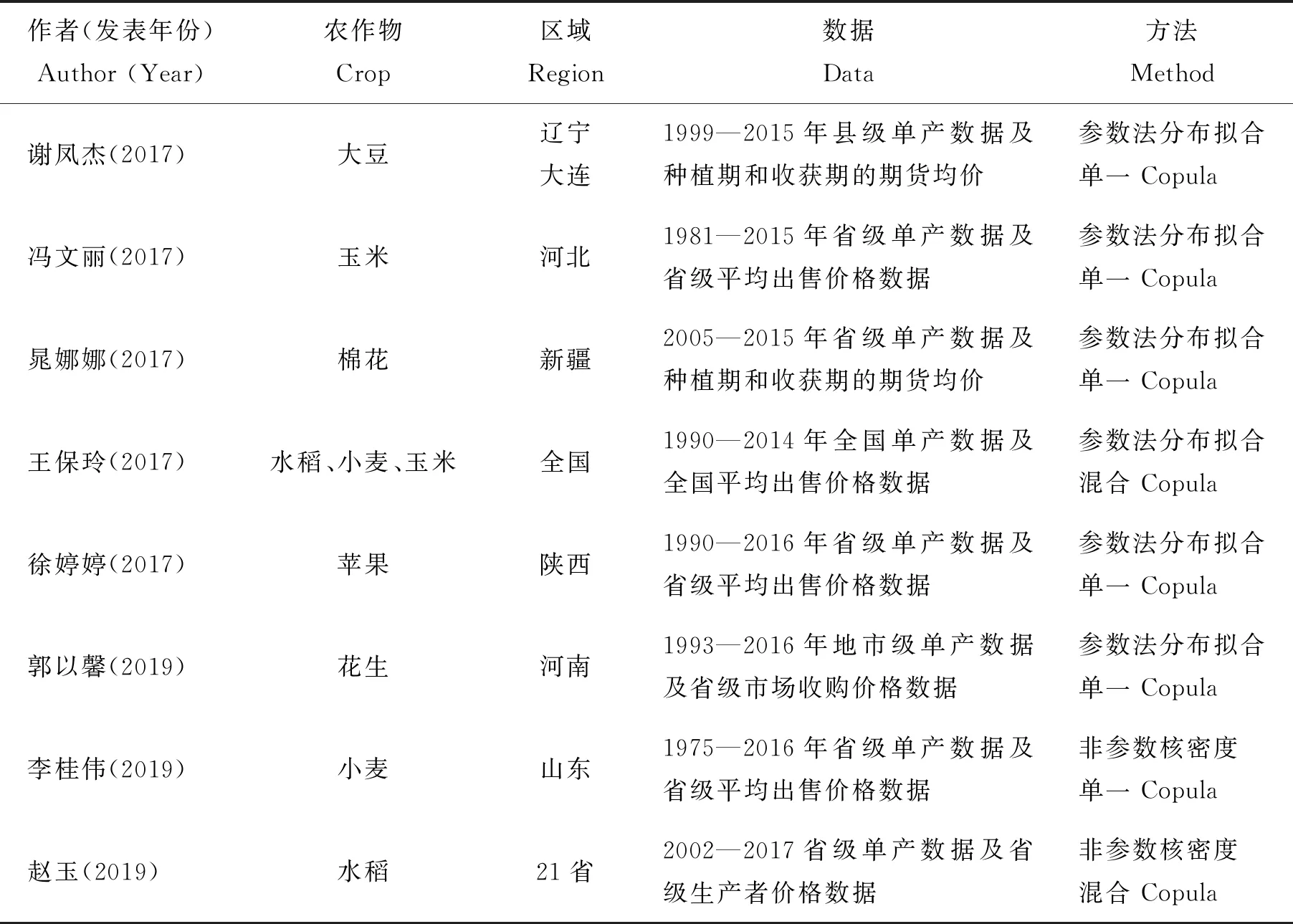
表1 国内农作物收入保险费率研究的部分文献情况Table 1 A part of literatures on the research of crops income insurance rate in China
在选择Copula函数时,现有文献大都预设Normal、Frank、Clayton、Gumbel和t-Copula 5种Copula模型形式,然后利用最小欧氏距离法选择最优的Copula,即与经验Copula之间的平方欧式距离最小的Copula为最优。但在实际应用中,拟合优度相近的两个Copula函数,费率厘定可能存在较大差异,导致结果的不稳定。例如测算河北省玉米收入保险费率时[6],Clayton与Gumbel Copula平方欧式距离的差距仅为0.000 049%(两者的平方欧式距离分别为0.012 199 782与0.012 199 776),但Clayton的kendall秩相关系数是Gumbel的1.87倍;在测算山东省小麦收入保险费率过程中[12],Clayton与t-Copula平方欧式距离的差距为0.48%(两者的平方欧式距离分别为0.041 8与0.040 6),但两者的kendall秩相关系数却有正负之别。尽管有的文献采用混合Copula方法增加拟合优度[9,13],但仍需在预设Copula函数形式的基础上进行参数估计。因此在样本量较小的情况下,个别异常样本将对估计结果产生重大影响,导致估计结果的不稳定。
综上,基于我国农作物单产和价格数据的小样本特征,为提高收入保险费率厘定的稳定性,增加估计结果的可靠性,亟需探讨区别于现有范式的保费定价方法。黄崇福[16-17]提出了一种处理小样本问题的有效方法,即信息扩散技术,通过扩散算子将单个样本点的信息扩散为一个区域模糊信息,从而扩大样本点的信息表达范围。由于农作物的产出受到种植技术、良种化肥等要素投入以及气候状况等条件的影响,农产品的价格由产出水平、市场状况等多种因素决定,每个因素的变化都会引起难以预测的数据变化,因此小样本的单产和价格数据以及两者之间的关系都具有一定的模糊性,每个样本点都可以作为“周围未出现样本点的代表”,运用信息扩散技术将样本点的信息进行扩散,可以实现样本量的扩展,增加厘定费率的置信水平。一维信息扩散模型在我国农作物成本保险的费率厘定中已有较多应用[18-19],二维信息扩散模型在灾害评估领域应用较少,郭树军等[20]通过建立雨强和水深两种数据的信息扩散模型,对城市内涝风险进行了评估,但目前还鲜有文献在收入保险费率厘定中应用二维信息扩散模型。因此本研究试图利用二维信息扩散模型厘定我国收入保险费率,同时对单产数据和价格数据进行信息扩散,将二维数据样本扩展至二维空间,以提高收入保险费率厘定的稳定性和可靠性,同时为我国收入保险费率厘定提供方法借鉴。
2 方法和步骤
利用二维信息扩散模型厘定收入保险费率,其方法设计和计算过程可以分为如下4个步骤:
2.1 根据样本数据,构造信息扩散点
设X与P分别代表去趋势后的单产和价格的RSV样本序列,按照式(1)的规则要求可以分别构造出单产和价格RSV样本的信息扩散点(论域)U,V,构成二维信息扩散向量U×V。
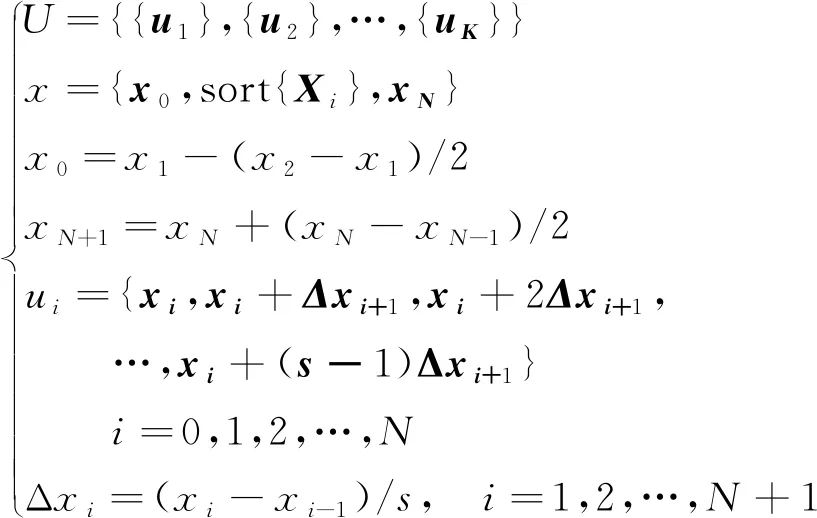
(1)
式中:sort{·}表示对集合{·}中的元素进行从小到大排序。若将二维数据视为平面上点的位置坐标,{ui}表示xi对应扩散点的横坐标集合,{vi}表示pi对应扩散点的纵坐标位置集合,{ui}中的任一元素uk与{vi}中的任一元素vj组成一个信息扩散点(uk,vj),Δxi与Δyi为样本点(xi,yi)对应横坐标与纵坐标的扩散步长,s为每个样本点确定的信息扩散点个数。
现有文献大多在样本点的最大值与最小值之间进行均匀布点,此处我们选择非均匀布点。根据极大似然估计原理,概率越大的事件越可能发生,则现有样本点出现的位置代表着事件最可能发生的位置,现有样本点代表了总体分布的特征,总体中的样本点应该具有类似的疏密程度,即样本点在空间上分布较为紧密的区域,总体分布的样本点在该区域处也应出现最多,这样不但能将现有样本信息在最可能的论域中扩散,而且能够反映二维数据之间的非线性特征。数据仿真模拟结果显示非均匀选择样本点信息扩散后能够得到更优的估计结果[21],因此本研究的信息扩散点以非均匀的方式进行确定,即每个样本点信息扩散的步长Δxi与Δyi取决于横坐标xi与xi-1的距离以及纵坐标yi与yi-1的距离。
根据上述扩散点生成办法,共生成K=J=(N+1)×s+1个组合数据,确定出((N+1)×s+1)2个二维样本扩散点(uk,vj)。
2.2 利用二维信息扩散模型,计算扩散后的样本信息
信息扩散类似于热力传导,样本点按照“就近原则”将自身信息传递给上述((N+1)×s+1)2个扩散点,距离样本点越近所得信息越多,越远所得信息越少。正态扩散模型是最常用的信息扩散形式,二维正态信息扩散模型如式(2)所示。
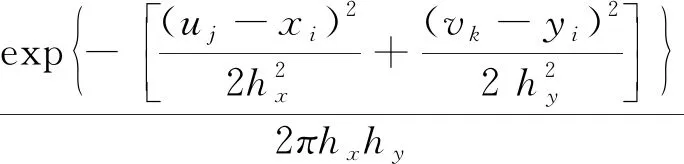
(2)
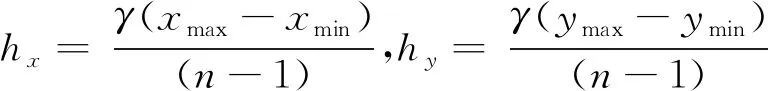
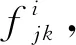
(3)
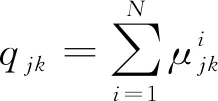
(4)
2.3 根据扩散结果,测算收入概率分布
参照Copula模型中利用Kendall-τ秩相关系数研究单产与价格之间相关关系的方法,本研究利用Kendall-τ秩相关系数的定义计算信息扩散点的秩相关系数。假设(u1,v1)和(u2,v2)是(U,V)的两个扩散点,若(u1-u2)(u1-u2)>0,称(u1,v1),(u2,v2)之间是和谐的,若(u1-u2)(u1-u2)<0,则两者之间是不和谐的,Kendall-τ秩相关系数为和谐概率与不和谐概率之差,计算公式如式(5)所示。
τ=P((u1-u2)(v1-v2)>0)-P((u1-u2)(v1-v2)<0)
(5)
2.4 厘定收入保险的费率
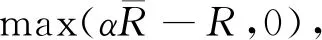

(6)
3 估计效率的模拟与比较
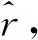
定义平方相对误差的均值(Mean of squared relative bias,MSRB)及平方相对误差的标准差(Standard deviation of squared relative bias,SSRB)作为衡量费率厘定效率的具体指标,如式(7)所示。
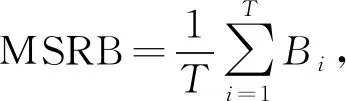
(7)
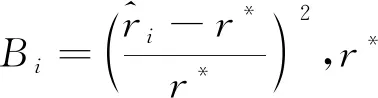
三种方法费率估计的MSRB与SSRB随样本数量的变化情况如图1和2所示。
从图1和2中可以看出:1)随着样本量的增加,3种估计方法的MSRB与SSRB都逐渐降低,说明样本量对收入保险的费率厘定有较大影响,且样本量越小该影响越大,因此针对我国小样本数据特征需要采用精确的方法进行费率估计;2)二维信息扩散模型在3种方法中具有更小的MSRB与SSRB,说明小样本情况下二维信息扩散模型的估计值更接近真值,具有更好的稳定性,并且样本量越小,信息扩散方法的优势越明显。
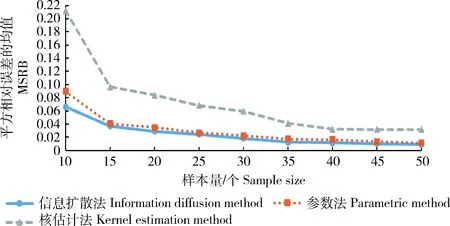
图1 正态分布估计值的MSRB比较Fig.1 Comparison of normal distribution MSRB
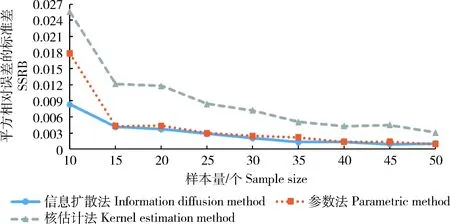
图2 正态分布估计值的SSRB比较Fig.2 Comparison of normal distribution SSRB
在边缘分布函数形式选择正确的情况下,“参数法”与“信息扩散”法的估计效率基本相同,但实际计算过程中由于存在分布形式选择偏误,参数法的估计效率有可能更低。例如若将x与y的总体边缘分布都改为威布尔分布(2)用威布尔分布和正态分布作比较,说明分布形式对费率估计的影响较大。,x~wbl(1,1),y~wbl(1,2),边缘分布仍假设正态分布进行估计,按上面的方法重新计算3种方法的MSRB与SSRB,其随样本量的变化情况如图3和4所示。从中可以看出:1)费率估计效率受分布形式选择的影响较大,在样本量较小的情况下,一旦分布选择错误,则费率厘定结果将与总体存在较大偏差;2)在威布尔分布情况下,“信息扩散”法仍然具有较好的小样本估计优势,即在3种方法中具有更小的MSRB与SSRB。
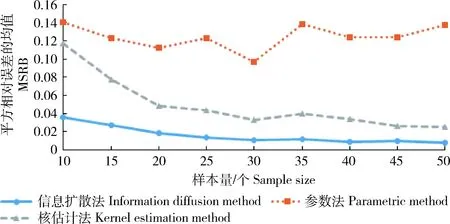
图3 威布尔分布估计值的MSRB比较Fig.3 Comparison of Weibull distribution MSRB
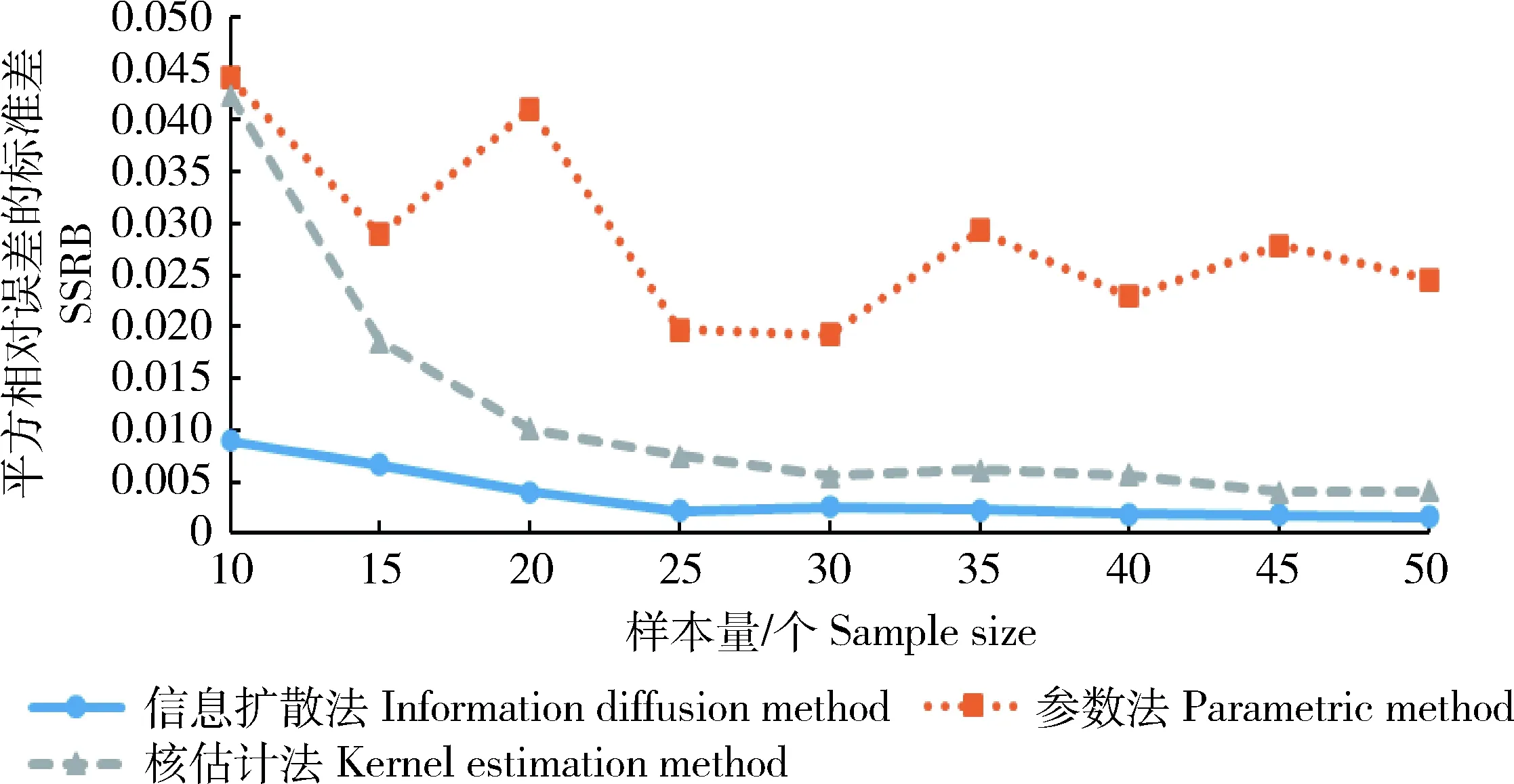
图4 威布尔分布估计值的SSRB比较Fig.4 Comparison of Weibull distribution SSRB
4 一个算例:河北省玉米收入保险费率的测算
玉米是重要的粮食作物和饲料作物,同时又是工业加工的重要原料,对国民经济发展起着重要作用。本部分以河北省玉米收入保险为算例,验证二维信息扩散模型在小样本情况下费率厘定的可行性与可靠性。选取1981—2018年河北省玉米单产及平均出售价格作为基础数据来进行玉米收入保险纯费率厘定,数据来源于《全国农产品成本收益资料汇编》[23]。数据的选取基于如下考虑:1980年我国开始在农业生产中推行家庭联产承包责任制,土地政策的改革极大地影响到农户的生产积极性,农业生产技术、方式和种植结构都有显著变化,势必影响到玉米单产的增长模式和趋势,因此本研究选择的研究期间为1981—2018年。
由于技术进步等因素的影响,玉米单产存在一定的增长趋势,同时由于通货膨胀等因素的影响,玉米单价也存在一定的增长趋势,因此需通过趋势拟合计算得到单产和价格数据的RSV序列。对农作物单产和价格数据的趋势拟合有多种方法,主要包括直线滑动平均法[1]、HP滤波法[24]、回归分析法[13]、小波分析法[12]等方法,各种方法具有不同的优势和缺点,本研究利用非参数局部线性加权法估计数据趋势,该方法能更好地克服其他方法中的模型设定和参数选择问题,具有更优的拟合效果和更小的估计误差[25]。单产和价格的原始数据及估计趋势如图5和6所示。
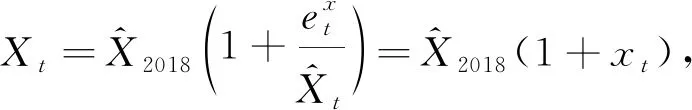
(8)
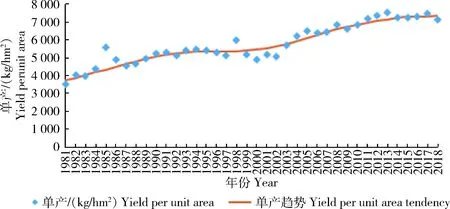
图5 河北省玉米单产及趋势拟合Fig.5 Corn yield per unit area and tendency in Hebei Province
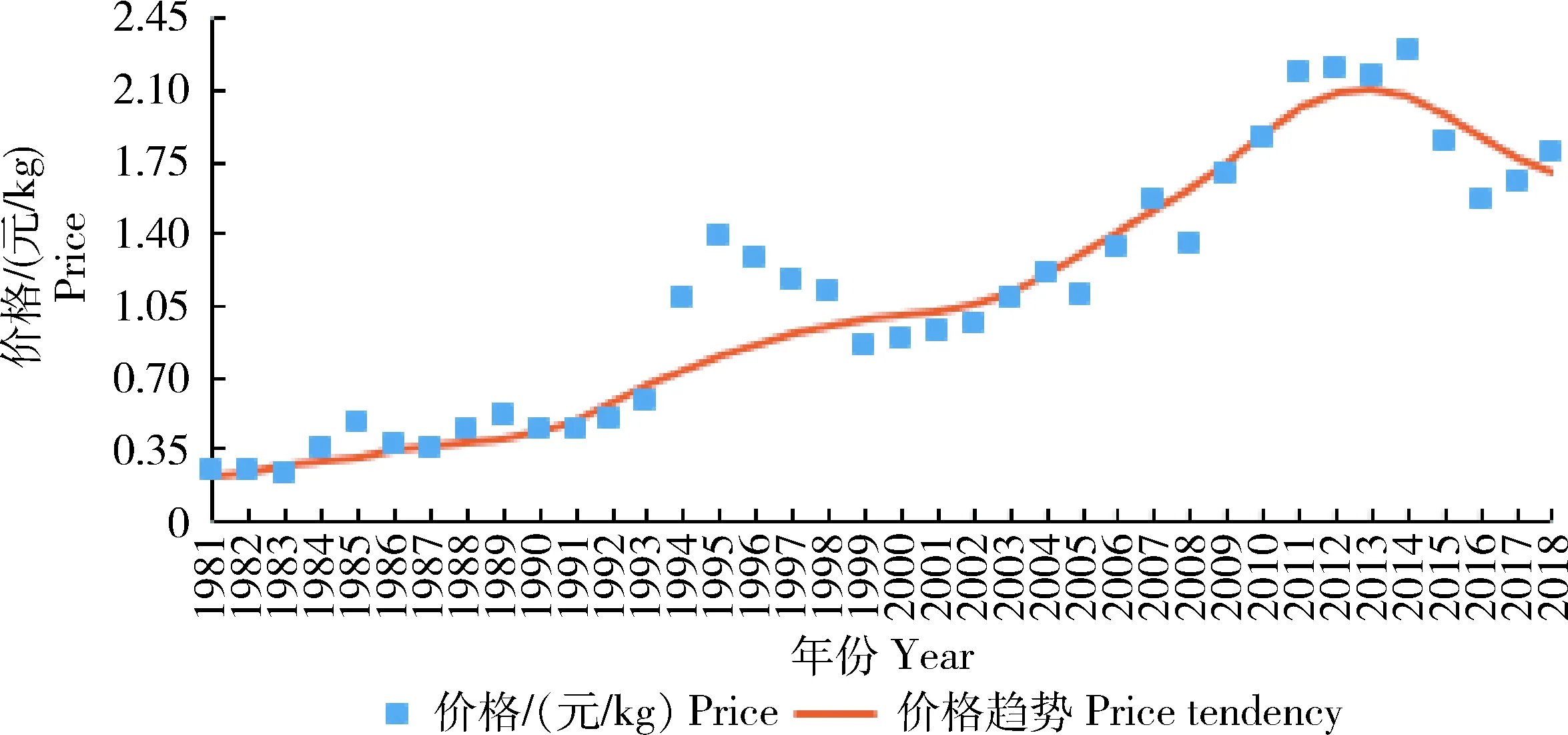
图6 河北省玉米价格及趋势拟合Fig.6 Corn price and tendency in Hebei Province
利用MATLAB计算得到河北省玉米单产和平均出售价格的波动率,其描述性统计量如表2所示。
从表2可以看出,河北省玉米单产波动率最大值为0.287 7,最小值为-0.106 0,标准差为0.065 0,峰度系数(9.954 5)远大于正态分布的峰度系数3,表明与正态分布相比数据具有明显的尖峰特征,偏度系数(1.842 3)表明分布向右倾斜,玉米出现增产的概率高于减产概率。玉米价格波动率最大值为0.711 3,最小值为-0.176 8,标准差为0.207 4,峰度系数(4.534 9)大于正态分布的峰度系数3,表明与正态分布相比数据具有尖峰特征,偏度系数(1.390 1)表明分布向右倾斜,玉米价格上涨的概率略高于下跌的概率。
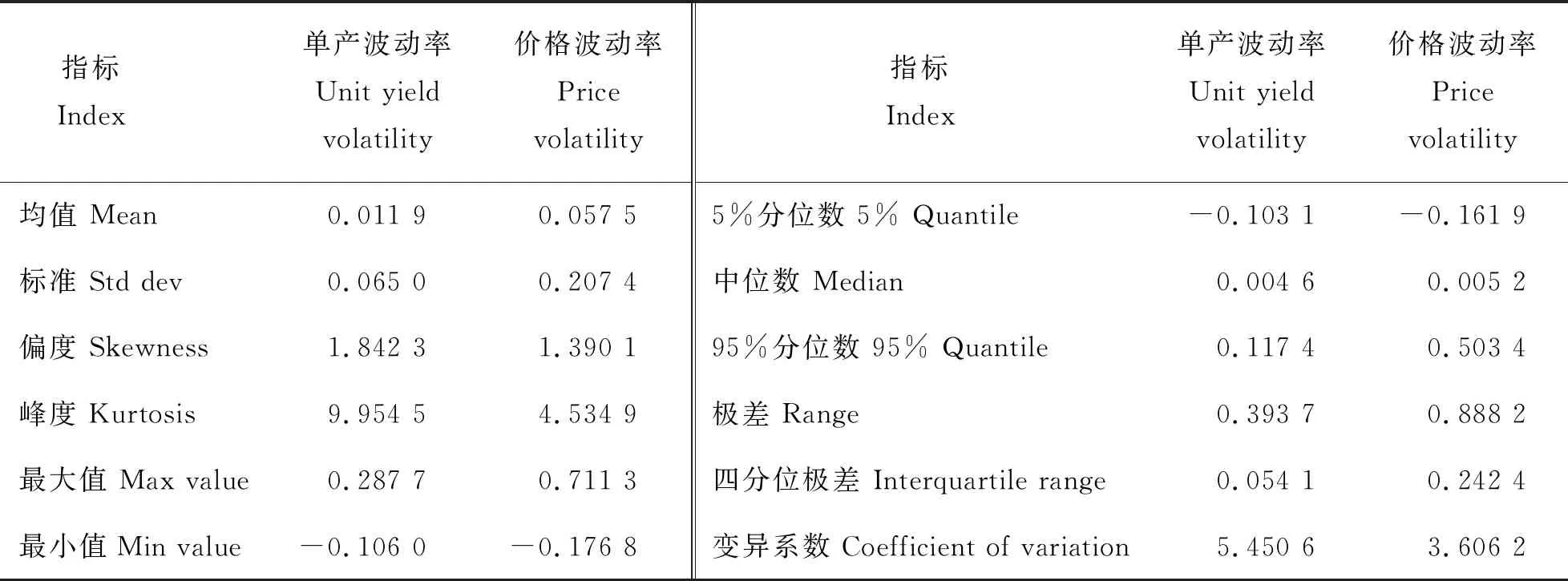
表2 单产与价格波动率的描述性统计量Table 2 Descriptive statistics of unit yield and price volatility
从图7单产及价格波动率的直方图及正态分布拟合情况也可以看出,河北省玉米单产波动率和价格波动率都与正态分布具有较大差距,且较难用某种经典分布进行分布拟合。
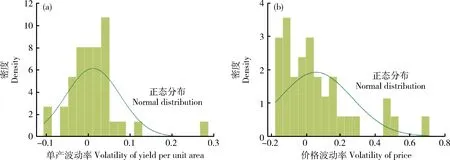
图7 河北省玉米单产波动率与价格波动率直方图Fig.7 Histogram of corn yield per unit area volatility and price volatility in Hebei Province
河北省玉米单产和价格波动率数据共38个样本,将单产与价格波动率(xi,yi)作为样本点进行二维信息扩散,每个样本点确定的信息扩散点个数s设置为5,计算得到((N+1)×s+1))2=38 416个样本扩散点(uj,vk)。根据公式(8)计算得到信息扩散后单产和价格模拟数据,其联合分布概率为pjk。单产与价格数据联合分布的直方图如图8所示。根据信息扩散后的单产和单价数据,计算得到农户单位面积的收入Rjk=xj×yk,其概率为pjk,直方图如图9所示。从中可以看出收入分布是右偏的,且具有较为明显的双峰分布和右拖尾特征。
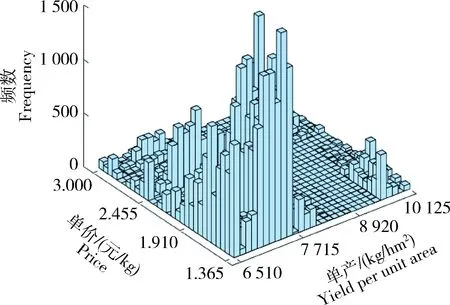
图8 信息扩散的产量与价格联合分布情况Fig.8 Joint distribution of output and priceunder information diffusion
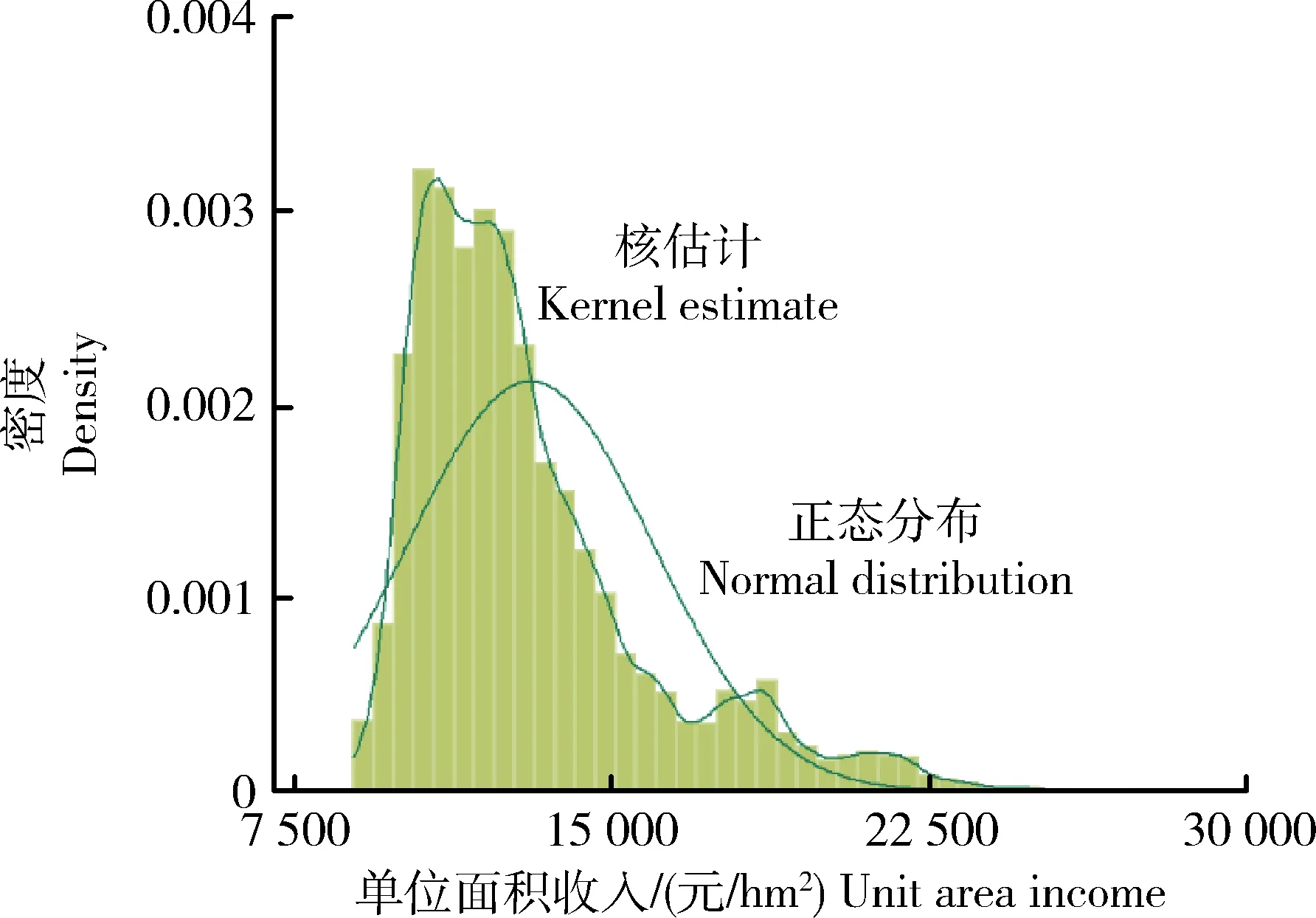
图9 收入分布拟合情况Fig.9 Fitting situation of income distribution
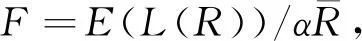
5 结论与讨论
5.1 结论
准确厘定费率是农作物收入保险能够持续发展的基础和关键。在我国农作物收入保险开展初期,需要根据数据特征和研究需求选择更加合理的数据统计方法,以期得到更加精准的保险费率。本研究阐述了Copula方法在我国农作物收入保险保费厘定过程中的优势和不足,基于小样本的数据特征,引入二维信息扩散模型,系统设计了利用信息扩散模型厘定农作物收入保险费率的方法和步骤。以河北省玉米收入保险为例,验证此方法的可行性,计算得到河北省玉米收入保险的纯费率为8.29%。
信息扩散模型不用预先选择某一边缘分布形式,也不用预先给定Copula函数,即可找到能够描述相关性、易扩展且计算较为简单的二维概率分布模型。从数据模拟结果看,在小样本情况下,相比Copula函数,二维信息扩散模型对费率的估计结果更接近真值,更稳定(标准差更小),因此二维信息扩散模型是进行农作物收入保险费率厘定的一种有效方法。信息扩散模型给我国农作物收入保险的定价方法提供了备选方案,为估计结果的比较和费率优化提供了方法基础。
5.2 讨论
需要说明的是,由于数据获取困难,本研究仅具有农作物收入保险费率厘定的方法论意义,测算出来的费率结果不能直接应用于实际操作。第一,保险公司运用此方法厘定实际费率时,须对数据进行优化,收集市、县、村或者农户等更小单位的农作物单产数据和反映市场行情的随机价格变动数据,以得出更为精准的实际费率。第二,美国的收入保险定价较为成熟,不同的保险产品使用的价格数据指标不同。CRC和IP利用农产品市场价格来测算价格风险,RA利用现行年份的期权价格与期权期货合约的偏离程度来测量价格波动。我国的农产品市场价格数据较易收集,并且能够反映出当年价格的整体情况,因此在验证二维信息扩散模型厘定收入保险费率的可行性时,本研究使用河北省50 kg玉米平均出售价格代表玉米市场价格。
农业保险在保障粮食安全的同时也在粮食价格形成、农村金融制度创新、农业供给侧结构性调整等农业发展改革中扮演着重要角色,已成为国家进行宏观调控的配套措施和重要抓手。从国外发展和国内试点情况看,收入保险的保障水平更高,且概念较为直接和简单,更容易被农户所接受,因此将成为未来我国农业保险的主要保险产品。收入保险的费率厘定已经成为理论和实践的关注对象,《关于加快农业保险高质量发展的指导意见》中指出,要“建立科学的保险费率拟订和动态调整机制,实现基于地区风险的差异化定价,真实反映农业生产风险状况”,因此应该利用多种统计技术发展精准厘定费率的方法,为收入保险的开展提供理论和方法基础。
