动态时间帕累托最优电子采购多属性谈判模型

曹慕昆,王 刚,张奇志

(1.厦门大学管理学院,福建厦门361005;2.弗吉尼亚理工大学商学院,弗吉尼亚美国24060)

1 引 言

随着互联网技术的高速发展,越来越多的企业采用电子化交易方式,而在交易电子化的链条当中,作为最前端的电子化采购起着举足轻重的作用[1,2].传统企业采购是典型的非信息对称博弈过程,选择供应商是首要的任务,然而,在大量的供应商中进行选择给企业采购人员带来沉重的工作负担,导致采购决策效率低下[3].特别是中小型企业,由于不具备大型企业在市场、渠道、信息、资源上的优势,更期望使用电子化采购来打开市场,实现物资供应各环节间的相互制约和控制,避免暗箱操作[4].电子采购在提升信息透明度、降低企业采购成本、优化库存结构、提高工作效率和物资管理水平等方面发挥着越来越大的作用[5,6].

电子采购是B2B电子商务的关键组成部分,允许买方在全球范围内选择供应商,因而需要先进的交易机制支持.电子采购机制主要有逆向拍卖和谈判两种.逆向拍卖在一个买方和多个卖方之间展开,多数情况下针对价格单一属性进行交易[7,8],而谈判的形式更为灵活,可以双边抑或多边,谈判内容可以是包含价格在内的多个属性[9−11].逆向拍卖被诟病的主要问题是仅关注买方的收益,而忽视卖方的利益所得,从而可能影响供需双方的长久合作[12],而谈判能够帮助买卖双方达成更为均衡的协议,从而保证双方的联合收益[13].目前,谈判已经可以通过电子谈判系统(ENS)在线完成,各种各样的电子谈判系统被开发出来[14],因此技术上不存在障碍.综合考虑,为了保护买卖双方的利益,本文选择谈判作为电子采购的交易方式加以研究.

现实中,企业的采购谈判很少只针对价格进行,而是涉及多个属性,如:价格、数量、交货期,保质期等.此类谈判也称为多属性谈判,任何一个属性不能达成一致都会导致整个谈判的失败[15].其关键问题是买卖双方在多个属性之间进行权衡(trade-off)[16],即通过在偏好度低的款项上让步,以争取在偏好度高的款项上达成一致,保证己方收益的同时,又不损害对方的利益,从而实现帕累托最优(Pareto-optimal)[17,18].一个帕累托最优解是不损害对方利益就无法进一步改进的解,也就是说,如果一方想获得比当前帕累托解更多的收益,系统中其他方就必须有所损失[19].因此,多属性谈判更适合现实中企业以共赢为目的的协商合作.经济学和人工智能都有对多属性谈判展开研究.经济学研究聚焦于谈判的最优机制和均衡策略.然而,由于多属性谈判问题的复杂性,很难基于非合作博弈理论构建严谨的模型与分析,就想出一些简化的办法,比如issue-by-issue谈判[20].其基本假设是属性之间相互独立,互不影响,但这明显与现实不符.现实中,谈判者会综合考虑各个属性,相互权衡.由此产生围绕帕累托最优和纳什均衡解的simultaneous 谈判[21].在合作博弈领域,纳什和其他一些学者致力于设计公理系统求解谈判问题,并且设计方法去找寻谈判模型的帕累托解.然而,无论是合作型抑或是非合作型博弈论的前提假设都过于严格,很难在现实中得以满足[19].因此,研究多属性谈判的人工智能方法应运而生.

人工智能致力于使Agent自动处理谈判过程,尽管结果可能不是最优[22,23].其主要方法是,把多属性谈判问题转换成一个多目标优化问题,也称多准则决策(multi criteria decision making,MCDM)[24],每个Agent的效用函数即是系统的一个子目标,目的是尽可能最大化每一个子目标.然后,用智能算法求解该多目标优化模型,得到帕累托最优解集.注意,求解结果是一个解的集合,而不是唯一的最优解.多属性谈判的最终协议解是从帕累托最优解集中选择出来的.买卖双方Agent需要在这些解当中进行讨价还价,从而得到双方都能接受的解为最终谈判解[17].

然而,由于多目标优化问题求解的复杂性,很多研究刻意将其简化为一个单目标优化问题.此类情况几乎代表了国内期刊发表的主流.如王高飞等将买卖双方效用函数简单相乘,得到一个需要最大化的单目标函数,用BP 神经网络和遗传算法相结合求出谈判最优解[25].蒋国瑞等将买卖双方效用函数简单相加,然后用人工免疫算法求解得到谈判最优解[26].陈培友等将马尔科夫链应用于属性偏好调整中,也是将买卖双方效用函数简单相加,用遗传算法求得谈判最优解[27].高珊等使用人工蜂群算法求解多属性谈判模型,方式上比前三篇复杂一点,目标函数不是简单加总,而是给每个Agent的效用函数添加一个权重系数,但本质上还是单目标优化[28].这种将多目标简化为单目标优化问题的做法,主要有以下缺陷:1)子目标函数求和或者求积之后形成的单目标函数优化,并不能保证各子目标最优化,因此失去了多目标优化的意义,而且是已经被淘汰的做法.2)单目标优化得到的结果,对各个子目标而言是一个零和博弈,不能保证双赢局势.3)单目标优化只需保证一个目标函数最优,因此可解得唯一最优解,而不是一个帕累托最优解集,因此,不存在买卖双方讨价还价的过程,也就失去了谈判的意义.所以,正确的方法应该是要保留多目标优化模型的原貌,解得的结果应该是一个帕累托最优解集,然后Agent 在这个解集中选择优势点与对手谈判.这也正是本文所采取的解决问题的方法.

目前,求解帕累托边界主要有两种方法.第一种方法是,穷举出所有可能的谈判解,从而确定帕累托边界,这个边界也是真正的帕累托边界(true Pareto front),但是,这个方法多数情况下只具备理论可行性.典型代表是Yang 等提出的双边多属性人机谈判模型[29].该模型中,谈判发生在人和计算机之间,双方就买卖笔记本电脑进行包括价格、配置等属性在内的谈判.该系统并非真实的电子商务系统,买卖双方各属性的出价和对应的效用均是事先设置好的离散数值,因此,系统可以轻松获得整个谈判解空间情况.由于人的有限理性,无法直观地知道自己当前所处的效用水平,卖方机器会每轮给买方人四个建议解.这些解是机器保持当前自身效用水平不变的情况下,向帕累托边界方向做调整所选择的四个值.问题是,系统并不是直接把最优解,即帕累托边界上的解,提供给买方人,而是给四个点让人去选择,因此明显具有诱导性.公平的做法是,机器给人的建议解就应该是帕累托边界上的点,而不是让人去猜.但遗憾的是,Yang 等的工作无法计算出帕累托边界的位置.与之相比,本文解决了这一关键问题.

第二种方法是,通过求解多目标优化模型逼近帕累托边界,也称为最优帕累托边界(best Pareto front).一些智能算法,如:向量评价遗传算法(VEGA)、多目标遗传算法(MOGA)、小生境遗传算法(NPGA)、非支配排序遗传算法(NSGA)等,可以被使用[30].近期的代表工作是Pan 等使用改进的非支配排序遗传算法计算双边多属性谈判模型的帕累托边界[17].但是,Pan等的工作存在两方面问题.1)模型使用所谓半竞争机制,允许买卖双方Agent 交换谈判过程中自己对对手出价的效用评价,从而可能泄露自己的机密私有信息,与现实谈判不符.2)用于在帕累托边界上讨价还价的让步策略被设计为一个分段函数,尽管该策略相比于经典时间依赖策略(time-dependent)更加灵活多变,但策略曲线的变化还是由固定的参数来控制,并不能适时动态地对谈判情境进行响应.本文针对这些问题,设计有中间平台参与的系统架构,以及自适应让步策略,根据谈判对手出价的变化动态响应,以求快速达成交易.

本文阐述一个基于多目标优化的多属性谈判模型,采用快速非支配排序和精英策略的遗传算法加以求解.在求解出的帕累托边界上,采用动态时间约束策略辅助买卖双方讨价还价,最终达成交易.成果可以运用在电子采购中,以帮助企业提升采购效率,降低采购成本.

2 动态时间帕累托最优双边多属性谈判模型

模型构建过程包含两个阶段:第一阶段是多目标优化模型的建立,以及基于改进遗传算法NSGA-II的模型求解,得到帕累托边界;第二阶段是买卖双方在帕累托边界上讨价还价,达成交易的过程.

2.1 双边多属性谈判模型

由于多边谈判可以分解为多个相互独立的双边谈判,因此,不失一般性,本文研究双边多属性谈判模型,可以形式地定义为一个五元组

其中A表示参与谈判的Agent集合,Agi ∈A,i ∈(b,s),其中b表示买方,s表示卖方.X表示谈判属性取值向量,X=(x1,x2,...,xn)T是一个谈判出价方案,其中xj是第j个谈判属性的取值,1jn,n ∈N.W表示谈判属性的权重向量,W= (w1,w2,...,wn),且满足即所有谈判款项的权重之和为1.wij表示Agi对xj属性的权重,其值根据用户自身偏好来设定.例如,当wi1> wi2时,表示对于谈判属性x1和x2来说,Agi更偏好于x1.u(X)是谈判出价方案的效用函数.方案X=(x1,x2,...,xn)T的效用为

其中v(xj)为属性xj取值的量纲归一化结果.对于收益类属性

其中和分别为属性可取的最大、最小值.对于成本类属性的量纲归一化结果为

f(X)表示多目标函数,f(X)=[ub(X),us(X)]T,ub(X)和us(X)分别表示买(b)卖(s)双方的效用函数,双边多属性谈判所对应的多目标优化模型为

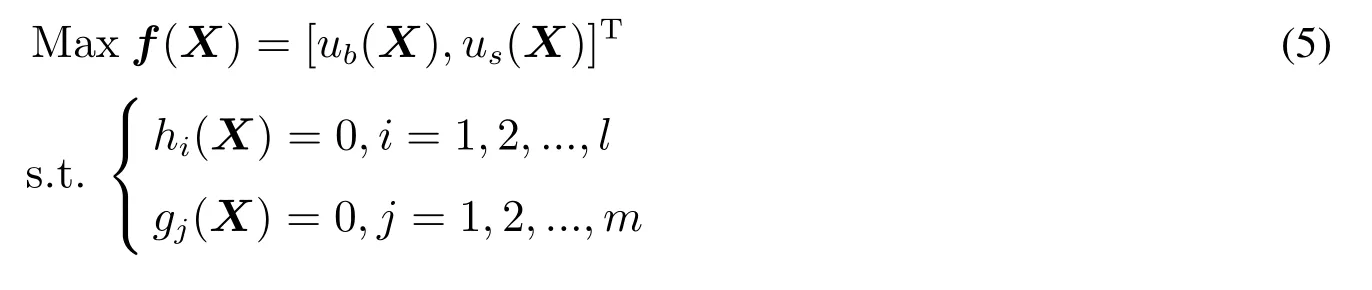
其中约束条件hi(X)和gj(X)确定出价方案向量X的可行空间,式(5)整体表示目标f(X)在约束条件下,各子目标效用函数都尽可能的最大化.

2.2 求解帕累托边界

如前所述,多属性谈判本质上是一个多目标优化问题.由于多个目标之间存在冲突,很难找到一个解使得所有的目标函数同时最优,而是存在一个帕累托最优解集.这些解无法在改进任何目标函数的同时,不削弱至少一个其他目标函数.将这些解在解空间中绘制出来即可得到帕累托边界.目前,主流求解方法是进化演算,其中以带精英策略的非支配排序遗传算法NSGA-II为代表[31].其算法可描述如下:

沿用前面的定义,Agent的一个出价方案为X= (x1,x2,...,xn)T,用一个染色体代表.在进化的过程中,交叉、变异等遗传操作应用于这些染色体中.出价方案所组成的集合O={X1,X2,...,XN}用染色体群来表示,作为一系列候选出价,其中N代表种群的大小.首先,系统建立一个随机的父代种群Pt={X1,X2,...,XN},进行非支配排序.然后,经过二进制锦标赛选择,重新组合,交叉操作后,创建一个大小为N的子代种群Ct.接着,将父代种群与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群Pt+1.最后,通过选择、交叉、变异等遗传操作产生新的子代种群Ct+1.依此循环,直到达到最大进化代数为止.由于NSGA-II 是通用算法,本文不再赘述,读者可查阅相关文献[17,31].

2.3 谈判系统架构

如图1所示,本文采用的系统架构是有第三方平台参与的谈判架构.Pan 等描述了一个买卖双方直接交互的模型,尽管双方并不透露各自的偏好,但其采用的半竞争机制(semi-competitive)允许双方将对方出价对于自己的效用透漏给对方.然而,现实中人是不会这么做的,而且也有泄露关键偏好信息的可能[17].与Pan的工作不同,本文的买卖双方不直接交换价格信息,更不会把自己关于对方出价的效用信息透露给对方,而是将出价信息和对谈判各款项的偏好信息提交给共同信任的第三方平台.第三方谈判平台负责交互协议控制,以及双方效用函数建模和随后的NSGA-II 帕累托最优解集计算,并将系统建议的帕累托最优解建议给买卖双方Agent,促成双方快速达成交易.这种模式也避免了Pan 的模型中,买卖双方Agent分别运用NSGA-II 算法可能造成的大运算量系统负担.最后,共同信任的第三方平台模式也符合当前电子商务的主流运营模式,如天猫、京东等,因此可以向这些电子商务平台推广,使本文的研究成果运用于B2C电子商务中.

图1 双边多属性谈判系统架构Fig.1 Bilateral multi-attribute negotiation system architecture

2.4 谈判协议模型

谈判协议定义了谈判双方的交互顺序与规则,如出价先后顺序,成交规则等.该模型中,买卖双方通过第三方平台交换信息,采取不同的谈判动作Act={offer,accept,reject}.其中offer 表示发出提议,accept 表示同意提议,reject表示拒绝提议终止谈判.Agent采取不同谈判动作的条件如下

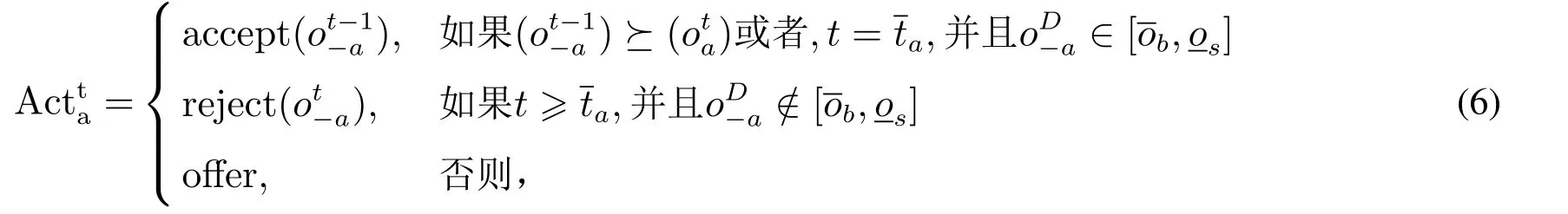
其中ota代表Agenta在t时刻的出价,a ∈(s,b)代表买方或卖方,−a是a的谈判对手,并且t1.Agent 接受对手出价的条件是:当对手的上一轮出价优于己方本轮出价或者,谈判到达自身设定的截止时刻ta时,对手出价在双方可行解范围之内(代表买方所能接受的最优出价,代表卖方所能接受的最优出价).Agent 拒绝对手本轮出价,并终止谈判的条件是:当谈判时间已经超出截止时间ta,而对手出价仍然在可行解区域之外.除此之外的情况,Agent 将采用offer动作与对手讨价还价.

2.5 帕累托边界上的谈判策略

系统获得帕累托边界之后,双方的谈判即在此边界上进行,而不用理会其他可行解区域的解,因为其他可行解不会优于帕累托最优解.可以想象,双方最初的出价都是最大化自身效用,接下来需要互相让步,以达成一致,因此,需要一个高效的谈判让步策略.本文提出一个动态时间依赖策略(dynamic time dependent,DTD),使Agent 能够依据对手的让步情况,用让步率描述,动态调整自身让步幅度,从而灵活应对复杂的谈判情境.不失一般性,以卖方应对买方为例,买方让步率为

其中utb表示在t时刻买方的效用.买卖双方的出价策略曲线均以Faratin 等提出的经典时间依赖策略(time dependent,TD)为基准[32].具体的算法步骤为:

当θ=1时,表示买方保持恒定让步幅度,此时卖方将保持已有谈判策略曲线不变予以应对.

当θ >1时,表示买方加速让步,即让步幅度逐渐增大,此时卖方将模仿买方的让步率,调整自身策略曲线,切换到能够促成交易的策略曲线上去.

当θ <1时,表示买方减速让步,即让步幅度逐渐减小,此时卖方将以1/θ为让步率(1/θ >1> θ),快速调整让步策略以迎合买方变化,从而快速成交.

当系统获得卖方的出价信息之后,会在帕累托边界上找寻最邻近点与之匹配,然后将这个点作为系统建议解返回给买方,买方将执行相同的过程来应对卖方的出价.此后,算法进入下一轮循环,共执行最大谈判轮数次循环.

本文所提出模型算法的时间性能由两个部分决定,遗传算法NSGA-II的时间复杂度,以及在帕累托边界上进行价格交互谈判算法的时间复杂度.其中遗传算法NSGA-II 的时间复杂度已经被大量的文献所研究,具体请参看[31].本文不再赘述,直接引用结果,即为O(mN2),其中m为目标函数个数,N为种群个数.本文的双边谈判模型有2个目标函数,因此,第一部分的遗传算法求解帕累托边界的时间复杂度为O(2N2),另一个部分,帕累托边界上的让步策略算法的时间复杂度可由算法最大循环次数决定,为卖方Agent的最大谈判轮数.在循环体内部,调用了一个求解到帕累托边界最邻近点的函数.该函数需要遍历帕累托边界上所有的点,最大循环次数为种群规模数N.因此,算法的近似时间复杂度为O().综合以上结果可知,本文所提出的多属性谈判模型算法的综合时间复杂度为

2.6 实例验证

A公司是中国汽车行业品牌前十强,其客车品牌有“国车”称誉.现公司需要采购一批新的客车发动机的关键零部件,有16个符合要求的供应商,需从中确定1 家.为提高采购效率,公司采用电子采购的方式与16 家供应商分别谈判,从中选择能够成交并最大化自身效用的一家进行交易.由于校企合作科研关系,本文作者事先走访调研了A公司,了解到采购所涉及的关键属性包括:价格x1(万元),保修期x2(月),和发货期x3(天)三项;并访谈了企业对各个谈判款项的偏好情况,设置属性的权重,如表1所示.

表1 买卖双方基本参数设置(所有数据来源于实际调研案例)Table1 Basic parameters of buyers and sellers(all data is from an actual case)

依据表1中的基本参数,可得多目标优化模型为

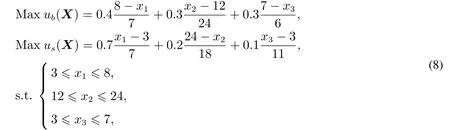
使用NSGA-II算法进行求解.设定种群大小为200、最大进化代数100,最大谈判时长为15轮,买卖双方初始策略为时间依赖策略TD空间中随机选取.解得帕累托边界如图2所示.接下来买卖双方Agent 在此帕累托边界上展开谈判.图3中横轴代表买方效用,纵轴代表卖方效用.圆型和菱形标记分别是买卖双方Agent 的出价,成交点用五角星表示.买卖双方经过9 轮谈判,最后以买方发出的提议成交,成交的买方效用为0.361 6,卖方效用为0.471 8.通过反归一化,该成交点的价格7.702 8 万元,保修期23.933 1个月,发货期3.090 5天.现实中的成交值为:价格77 028元,保修期是24个月,发货期是3 天.

图2 买卖双方Agent在帕累托边界上的谈判效果Fig.2 Negotiation effect of agents on the Pareto front

3 实验分析

3.1 实验设置

不同于前面有实用背景的实例验证,本节的实验分析主要通过大规模仿真模拟验证模型的算法性能.这里设计了两组自动谈判实验:第一组实验用于检验本文所提出的算法在促成谈判双方共赢方面的性能；第二组实验用于和领域代表性成果进行比较,全面检验算法的经济学指标性能.

在第一组实验中,共进行了200次模拟谈判,每一次谈判发生在一对买卖Agent 中.通过程序随机数设定,每个Agent都有自己独特的谈判属性偏好设置,这样就造就了200个不同的多目标规划问题.通过这200对Agent 的自主谈判,本文收集最终的谈判成交结果,计算每一对买卖Agent的最终效用值,做成散点图,直观地观察效用聚集情况,以发现算法在促成买卖双发达成双赢谈判解的统计效果.实验结果如图3所示,红点代表卖方效用,蓝点代表买方效用.可以看到400个Agent 的效用都向双赢效用基线0.5靠近.因此,证实了本文所设计的谈判模型可以有效地促成谈判双方达到共赢局势.

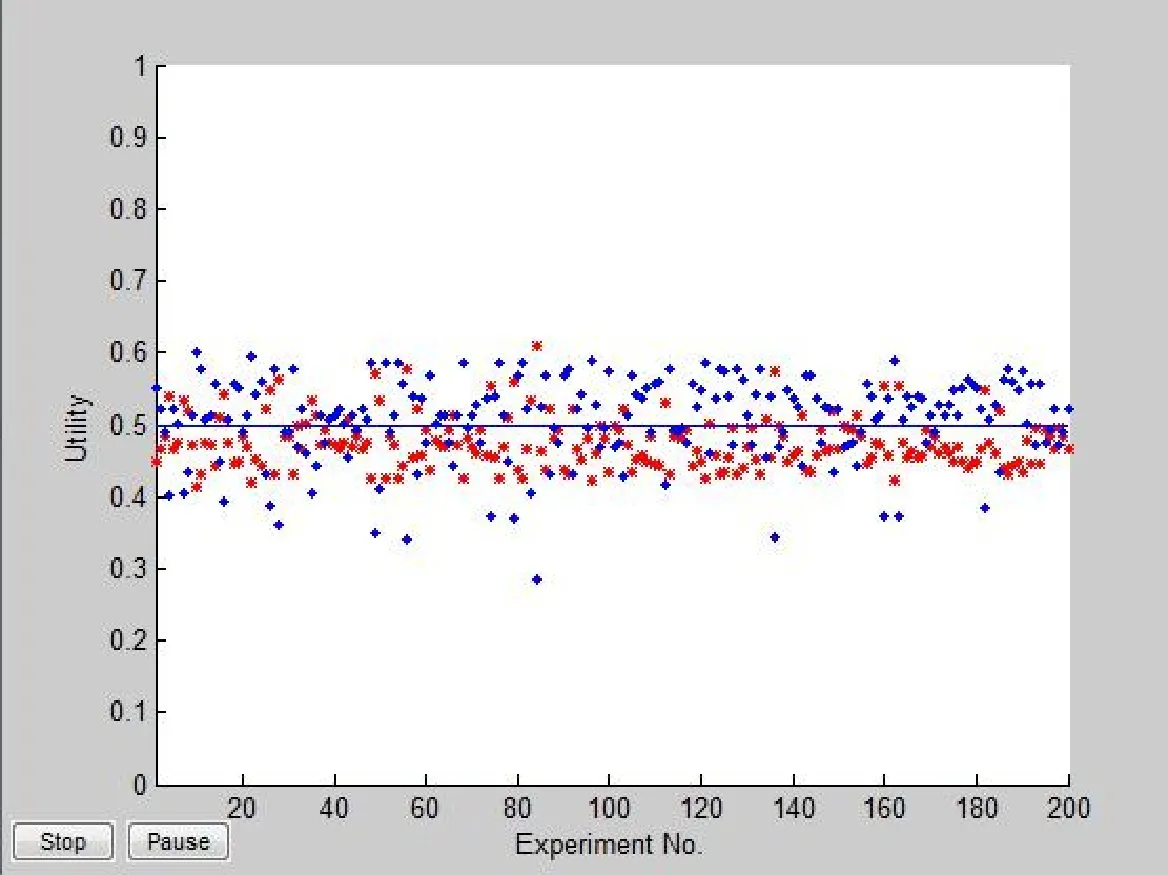
图3 多属性谈判模型在寻找双方最优的实验结果Fig.3 Multi-issue negotiation model is looking for optimal experimental results

在第二组试验中,选取目前代表性的多属性谈判策略模型Pan等[17]进行比较.选取该模型作为比较基准基于以下两点考虑:1)自动谈判是人工智能技术的重要研究领域,Pan等提出的模型发表于主流重要人工智能学术期刊,而且被领域内研究大量引用.2)从研究方法上看,该模型是首个使用人工智能方法求解多属性自动谈判问题的帕累托最优边界的成果,研究思路与本文的模型最为接近,具有突出的可比较性.3)Pan 等提出的模型同本文类似地分为两个部分,本文所要与之对比的,不是遗传算法求解帕累托边界这部分,而是比较如何在帕累托边界上进行谈判让步的策略算法.原因是遗传算法求解帕累托边界属于通用做法,无需比较.另一方面,本文所提出的有第三方平台参与的信息交换机制对帕累托边界上的谈判让步策略算法没有影响,所以不会影响两种模型之间的比较.Pan 的模型基于一个分段函数让步策略指导Agent 在谈判过程中做出让步,可以形式地定义为

其中T为谈判截止时间,a ∈[0,1],b ∈[−c,1−c],t1,t2∈[0,T],并且t1t2,λ1,λ2∈(0,+∞),c是一个常量,并且c ∈[0,1].

根据参数取值的不同,该分段函数可分解出八种情形,分别是Sinc-con,Sdec-con,Scon-inc,Scon-dec,Sinc-dec,Sdec-inc,Sinc-con-dec,Sdec-con-inc,描述了各种可能的复杂谈判出价情形.如Sinc-con-dec代表出价先上升,后保持恒定,再下降的山峰策略形态.而Sdec-inc描述了先降后升的山谷策略形态.伴随不同的参数设定,这些谈判策略曲线呈现出千变万化的状态.

3.2 实验结果

首先,本文提出的DTD策略和基准策略进行比较,直接P.K.具体地,买方Agent 采取Pan等提出的八种分段函数策略Sinc-con,Sdec-con,Scon-inc,Scon-dec,Sinc-dec,Sdec-inc,Sinc-con-dec,Sdec-con-inc,卖方Agent 采取DTD策略,分别进行200 次实验,总计1 600 次模拟谈判.表2的实验结果方差分析显示,除inc-con 策略双方效用相差不大外,其余对决中,采取DTD 策略的卖方效用均显著高于买方效用(p=0.000),平均高出56%.

然后,间接P.K.固定买方策略为经典的时间依赖策略TD,而卖方策略采取八种分段让步策略和DTD策略.分别进行200次实验,共1 800 次模拟谈判.实验结果如表3所示.

为了更好地测度模型帮助谈判双方达成共赢的效果,本文参考Ros 等的工作,采用效用积(UP)和效用差(UD)来评价双方的联合效用[33].理论上,效用积越大越好,而效用差由于代表双方效用的差异程度,双赢的结果应该是越小越好.二者的计算公式如下

从表4的单因素多元方差分析(MANOVA)结果可知,成交时间方面,DTD 与其他策略相比效果不是很显著,而在Agent个体效用和系统联合效用方面,比较效果相当显著.DTD策略的谈判结果就买卖双方个体效用而言,都显著高于其他策略,表示本文设计的DTD策略的确能够提升Agent 个体收益,同时也带动采用其他策略的买方Agent 显著提高了其自身收益.另一方面,从系统联合效用角度考察,有采用DTD策略的Agent参加的谈判,买卖双方效用积显著高于其他策略Agent谈判局势,表示确实提升了系统整体收益.但是同时,买卖双方的效用差也显著高于其他组,表示DTD策略在参比策略中较为强势,可能增大买卖双方的收益差距.

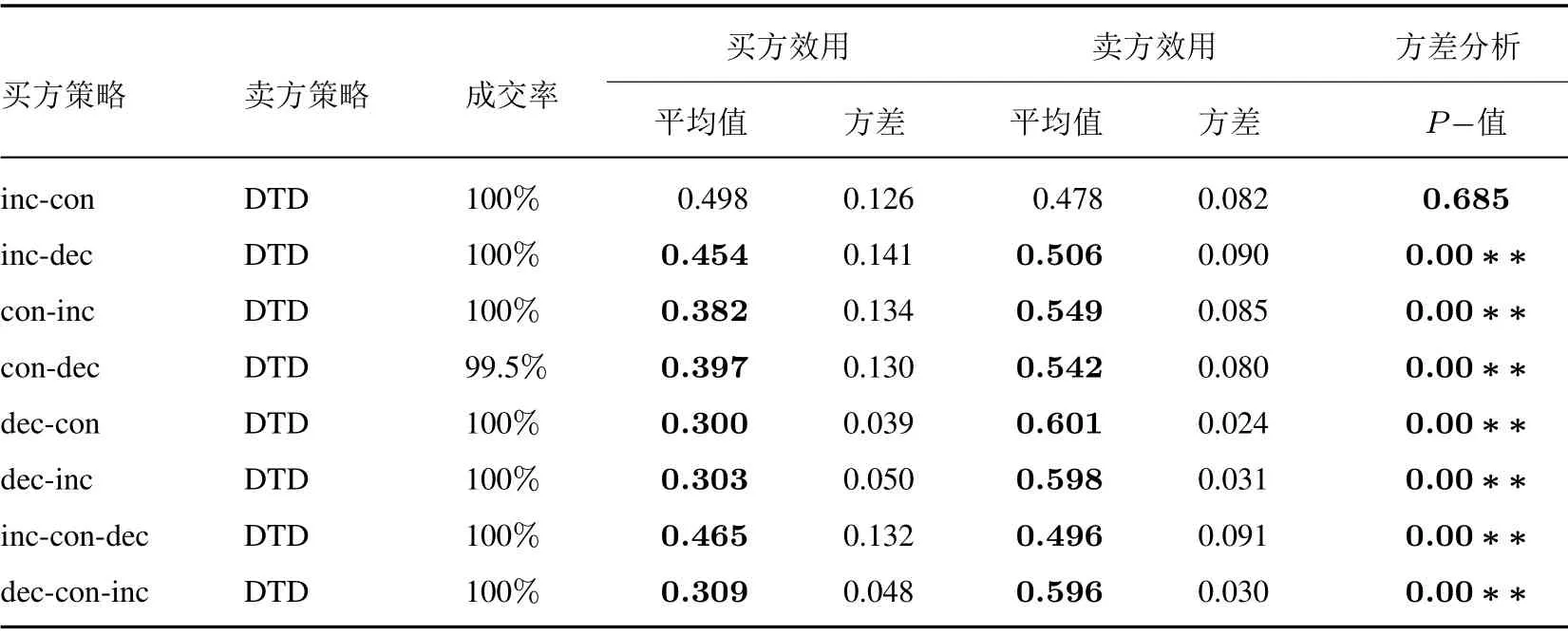
表2 DTD策略P.K.分段函数策略Table2 DTD strategy P.K.piecewise function strategy

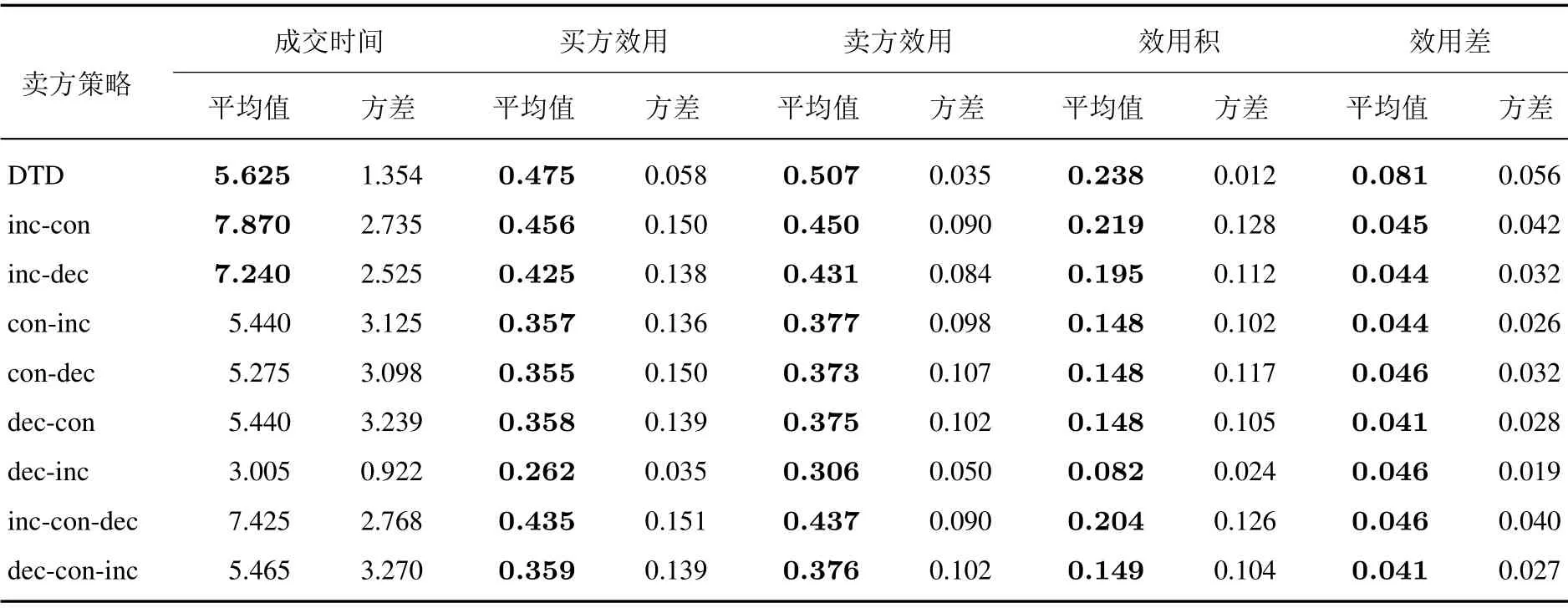
表3 固定买方策略,DTD策略P.K.分段函数策略Table3 Fixed buyer strategy,DTD strategy P.K.piecewise function strategy

表4 单因素多元方差分析结果(MANOVA)Table4 One-way multivariate analysis of variance(MANOVA)

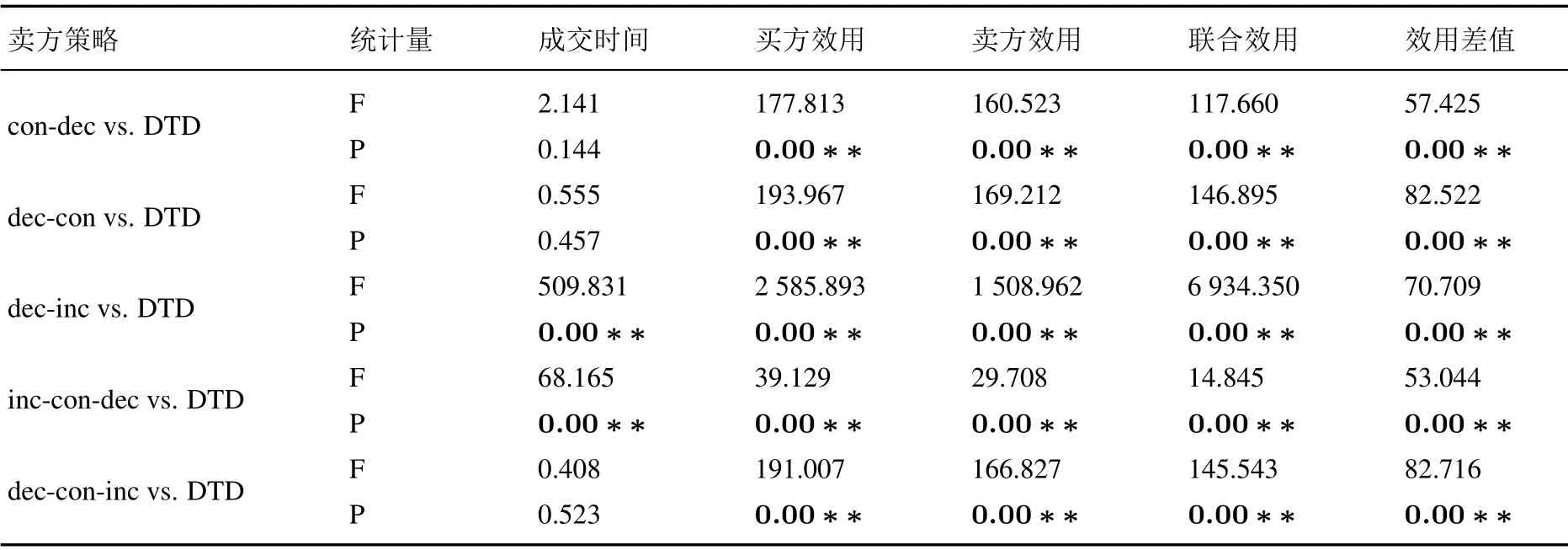
续表4Table4 Continues

4 结束语

本文将供应链电子采购环境下的双边多属性谈判问题转化为多目标优化问题,使用智能进化算法NSGA-II加以求解;进而设计动态时间依赖策略DTD,用以在帕累托边界上讨价还价.通过大量实验证实,模型有成交率高,成交速度快,经济效益好等显著优点,算法性能优于当前领域的主流研究成果.从实践角度,模型使用中间平台作为谈判媒介,能够保护买卖双方私有信息,提升商家和多个买家的谈判效率,降低交易成本.因此,可向B2C 电子商务平台,如京东、天猫等,进行推广.