考虑鲁棒性成本的多模式双目标项目前摄性调度优化

李 雪何正文王能民

(1.西安交通大学管理学院,陕西西安710049;2.过程控制与效率工程教育部重点实验室(西安交通大学),陕西西安710049)

1 引 言

项目调度中的大量研究问题致力于获得一定优化指标下的基准进度计划,如工期、成本、净现值等优化目标.这些研究大多假定外部环境是确定的,制定的最优进度计划可以按照预期逐步执行.但在项目的实际执行过程中存在各类不确定性,比如资源短缺、机器故障、气候恶劣、工期滞后、供货商延迟交付等情况[1].此时,原本制定的最优进度计划往往是不可行的,更无法保证项目执行的稳定性.所以,为了确保项目顺利实施,管理者希望制定具有鲁棒性[2]的进度计划.但是提升进度计划鲁棒性需要投入额外的资源或时间,发生鲁棒性成本.因此,在构建进度计划时不但需要最大化项目实施的鲁棒性,还需要最小化鲁棒性成本.本文研究如何调度项目的活动制定进度计划,实现鲁棒性和成本的双目标权衡优化.权衡两个目标一方面可以增强进度计划的抗干扰能力,另一方面可以有效避免在提升进度计划鲁棒性的过程中投入过高的成本、降低项目收益,最终达到以低成本稳定实施项目的目的.

项目成本与项目收益直接相关,是项目调度中重点关注的优化指标.其中,确定性环境下的时间/费用权衡问题是项目调度中广泛研究的内容[3−5],这类问题都假定环境是已知确定的,在项目实施过程中不会发生变化.项目进度计划在实际执行过程中常常受到各类不确定因素的干扰,影响项目进度计划的执行,使项目难以按期完成,增加项目成本、降低项目收益[6].因此,进度计划要能够抵抗、吸收不确定因素的干扰,即具有鲁棒性[7],鲁棒性越大,进度计划在执行过程中越有能力抵抗不确定因素的干扰.寿涌毅等[8]研究活动工期不确定情况下的鲁棒优化问题,张立辉等[9]将鲁棒调度中的时差概念与重复性调度方法结合,提出了适用于重复性项目的时差概念体系.王昱等[10]应用鲁棒优化调度方法解决医院手术时间不确定性的手术调度问题,采用两阶段方法求解.黄敏等[11]研究随机运输时间和成本下第四方物流的路径鲁棒优化问题,设计并改进蚁群算法求解模型并验证算法的有效性.Lambrechts等[12]研究在随机资源条件下获得稳定的基准进度方案,用基准计划与实际计划活动开始的偏差加权和衡量进度鲁棒性.本文同样是在不确定环境下进行鲁棒优化调度,但同时优化项目的鲁棒性和成本是一个多目标权衡问题,已有不少学者针对项目调度领域内的多目标问题展开研究,主要是工期–鲁棒性权衡问题、时间/费用权衡优化等.Van de Vonder等[13]探讨项目稳定性与工期的权衡问题,研究如何在活动间分配缓冲时间、项目缓冲和接驳缓冲.李洪波等[14]设计仿真方法与非支配排序遗传算法的混合优化算法,求解复杂产品研发项目多目标问题的Pareto 最优解,同时优化项目工期和成本两个指标.付亚平等[15]研究求解多目标优化问题混合算法,分解模型为多个子问题,获得较好质量和分布性的非支配解.Tabrizi等[16]提出一个鲁棒混合整数规划模型,最小化项目采购成本、最大化进度鲁棒性,并采用非劣排序遗传算法和改进版本的多目标差分进化算法进行求解.宋晓宇等[17]以最小化调度总费用和最大化应急点满意度为目标构建应急物资调度模型,然后应用粒子群算法实现多目标优化问题的求解.刘世新等[18]构建模糊多目标项目调度问题,设计遗传局域搜索算法求解生成近似有效解集,以便决策者进行权衡选择.在上述研究中,鲁棒性和成本是项目调度优化的重要指标,而且项目调度领域已有学者广泛研究多目标优化问题.在本文中,研究不确定环境下的鲁棒性和成本双目标优化问题.

在上述现实和理论背景下,本文研究不确定环境下考虑鲁棒性成本的多模式项目前摄性调度优化问题,以同时优化项目鲁棒性和考虑鲁棒性的项目成本为目标构建优化模型,在可更新资源和项目工期的约束下决策各活动的执行模式和开始时间.将双目标模型解剖为单目标子模型,设计迭代式遗传算法求解,获得鲁棒性高且成本低的进度方案Pareto解集供决策者权衡选择.在标准算例集合上进行算法对比测试,验证迭代式遗传算法的求解效果,并进行参数敏感性分析.论文首先界定研究问题,构建鲁棒性和成本双目标优化模型,借助算例说明鲁棒性和成本的权衡关系,通过子模型对模型深入分析,然后设计迭代式遗传算法求解,并在随机生成的标准算例集合上测试验证算法的有效性.

2 双目标优化模型

2.1 问题界定

本文研究的问题是调度AoN(activity-on-node)网络G=(N,A)中的活动i=0,1,...,n+1,其中N和A分别代表活动集合与活动间优先关系.项目网络中的活动从0∼n+1依次排列,其中活动0和活动n+1均为虚拟活动,分别表示项目的开始和结束,不占用时间和资源.活动间的优先关系保证活动只能在其紧前活动完成后开始.活动i以m= 1,2,...,Mi模式执行时每天需要消耗rimk(k= 1,2,...,K)单位可更新资源,工期为dim.在项目执行的每一阶段,可更新资源k的最大可用量为Rk.活动i发生延迟对于项目稳定性影响的权重为wi,资源k的单位时间使用成本为ck,D表示项目的最大截止工期.ESi和LSi分别表示采用关键路径法计算的活动i最早、最晚开始时间,St为t时刻正在执行的活动集合,Robu和TC 分别表示项目进度的鲁棒值和成本值.

用xim表示活动i是否以模式m执行,yit表示活动i是否在时刻t开始执行,是双目标问题的决策变量.确定活动i在不同模式和不同时刻下的变量xim和yit的值,就为其安排了确定的模式和开始时间,同时,活动的工期和结束时间也就确定了.项目中每个活动都确定了执行模式和开始时间、结束时间,就形成了项目的进度计划方案.

在实际项目调度中,进度计划常常受到外来因素的干扰,为了增强项目鲁棒性,在活动之间应当留有一定的时间缓冲,增强进度计划的抗干扰能力.活动i的缓冲时间表示在满足资源约束的条件下,不推迟紧后活动最早开始时间前提下活动i开始时间最大变化量,表示方式如下

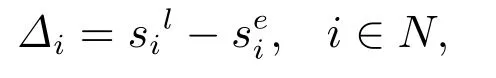
其中sei、sil为采用串行进度生成方案(serial schedule generation scheme,SSGS)方法在给定各活动的执行模式和执行顺序时计算得到的活动i的最早和最晚开始时间,保证进度方案满足优先关系约束、工期约束和资源约束,Lambrechts 等[12]提出该方法用于计算资源约束下的活动缓冲时间.再者,应用SSGS方法安排进度计划时,会在满足约束的条件下尽可能早地安排项目活动,所以有

按照进度方案计划,活动i在时刻开始执行直到结束.活动i实际执行过程中,若受到不确定因素干扰,开始时间发生延迟,在区间sei,sli内任一时刻开始执行,都能够有足量的资源保证活动的正常执行,而且不会推迟其紧后活动的最早开工时间.所以,该区间长度为活动i的缓冲时间.

由于不同活动延迟对于进度计划的影响不同,为不同活动添加缓冲时间对于进度鲁棒性提升的效果也不同.因此,需要对各活动缓冲时间设置不同的权重.累积不稳定性权重CIW(cumulative instability weight)计算方法如下

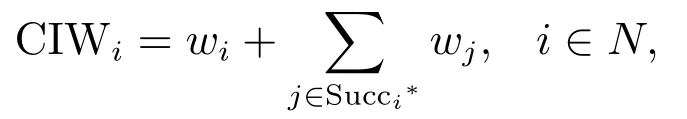
其中Succi∗表示活动i所有后续活动的集合,wi为项目管理者依据以往经验为项目各活动设置的权重,权重越大,表示该活动发生延迟时越难以调整纠正、对后续活动的不利影响越大.CIW越大,活动延迟对项目进度的影响就越大,所以在为活动添加相同缓冲时,CIW 大的活动可以更大幅度地提升项目鲁棒性.

项目活动缓冲时间越大,活动执行时越能够抵抗不确定因素的干扰,稳定性越强.由此,采用项目活动缓冲时间的加权和表示项目鲁棒值

项目鲁棒值越大,项目活动总体抵抗不确定因素干扰的能力就越强,项目执行过程越稳定,进度计划的鲁棒性越强.

项目成本包含两部分,其一是缓冲时间内项目活动占用资源成本,其二是项目活动实施时所消耗资源费用.具体表示如下

本文的研究问题可以界定为,在优先关系约束、工期约束和资源约束条件下,以同时最大化项目鲁棒值Robu、最小化项目成本TC 为目标确定各变量xim、yit的值,制定鲁棒性强且成本低的进度计划.

2.2 优化模型构建

依据问题界定中定义的各类参数和变量,构建鲁棒性和成本多模式双目标权衡项目调度优化模型如下,

上述各式构建了在优先关系约束、工期约束和资源约束的条件下,鲁棒值最大化、成本最小化的多模式双目标项目调度优化模型.式(1)为采用缓冲时间加权和表示的鲁棒值,是最大化的目标.式(2)表示考虑鲁棒性成本的项目进度计划各活动占用资源的总成本最小化,是项目执行过程各活动工期和缓冲时间范围内所占用资源消耗成本的总和.式(3)表示项目中各活动只能选取一种执行模式,式(4)表示活动在其时间窗内选取一个时刻开始执行.式(5)为紧前紧后活动间的优先关系,紧后活动的开始时间不早于其紧前活动的结束时间.式(6)表示项目的完成时间在最大截止工期之内,式(7)保证项目执行过程中每一时刻各类资源使用量均不超过其可用量.式(8)为缓冲时间计算式,式(9)、式(10)为决策变量的定义及取值.

经典的资源受限项目调度问题是在确定性环境下展开的强NP-hard问题[19],在满足优先关系约束和资源约束的条件下,制定项目进度计划方案优化一定的调度目标(工期、成本、净现值等).鲁棒性和成本双目标优化调度问题可以看作经典问题的拓展,当各活动缓冲时间为零、且只在活动执行期间供给资源时,双目标问题即为传统的成本最小化项目调度优化问题.因此,鲁棒性和成本双目标权衡项目调度问题也是强NP-hard问题.

应用上述模型,可以对鲁棒性和成本进行双目标权衡优化,确定各活动的模式和开始时间,制定进度计划,优选鲁棒值大且成本低的进度方案.

2.3 算例

下面用一个算例进一步阐述模型中鲁棒性和成本的权衡关系.算例活动网络图如图1所示.

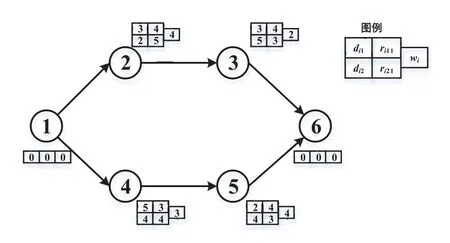
图1 算例网络图Fig.1 The network of a instance

图1给出了活动在不同执行模式下所需的执行时间、资源以及活动权重,设单位时间资源最大可用量为8个单位,资源单位时间使用成本为1,项目工期为10.令虚拟开始活动1在零时刻开始,虚拟结束活动6在项目工期处结束.

依据网络关系和活动参数,制定三个可行进度计划方案,图2中各灰色矩形分别表示不同的活动,括号内数字表示活动所选取的执行模式.

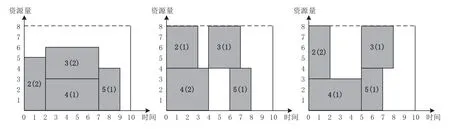
图2 三个进度计划方案Fig.2 Three schedules

在方案1中,只有活动3和活动5有缓冲时间,分别为3、1,总时差为4.根据成本和鲁棒值表示式计算可得,该进度方案的成本为61、鲁棒值为10.在方案2 中,各活动的缓冲时间分别为1、3、2、2,总时差为8,进度方案成本为80、鲁棒值为24.在方案3中,活动2、活动3 和活动5 的缓冲时间分别为3、2、3,总时差为8,该进度方案成本值为80、鲁棒值为28.

由算例的三个进度方案可以看出,缓冲时间增加,需要更多的资源,会发生鲁棒性成本,增加了项目总成本,但也会使得鲁棒值得到提升.对比三个方案可知,方案2、方案3较方案1而言,鲁棒值更大、消耗成本也更多.就方案2、方案3 而言,二者成本值相等,但方案3 鲁棒值更大,是更优的方案.在进行鲁棒性和成本双目标权衡时,需要不断剔除鲁棒值小、成本大的方案(如方案2),优选出鲁棒值大、成本低的进度方案(如方案1、方案3),供决策者根据自身偏好进行权衡取舍.

2.4 单目标子模型分析

为深入分析求解鲁棒性和成本双目标优化模型,将成本目标转化为约束条件,得到如下的鲁棒值最大化单目标模型

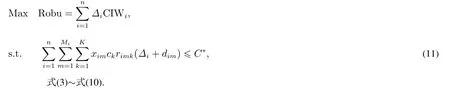
在存在预算约束的鲁棒值最大化单目标模型中,求得的最优解Robumax(C∗)必为双目标模型的可行解.另外,由于Robumax(C∗)为在预算不超过C∗时最大的鲁棒值,所以在双目标模型的解空间中,不存在支配(Robumax(C∗),C∗)的解,故鲁棒值最大化单目标模型的最优解必为双目标模型的Pareto解.

进一步地,变化鲁棒值最大化单目标模型中的成本约束值C∗求解多个单目标问题可以得到一系列双目标模型的Pareto解,示意图见图3.

由图3可以看出,逐渐变换C∗值,鲁棒值最大化模型的解空间将会覆盖整个双目标模型的解空间,相应的最优鲁棒值与其对应成本值形成双目标模型的帕累托前沿.由此,可以通过求解不同预算约束下的鲁棒值最大化问题来求解鲁棒性和成本双目标模型的Pareto最优前沿.

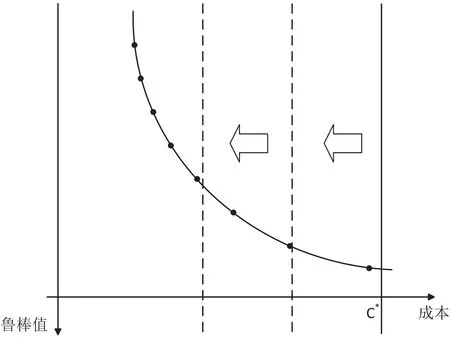
图3 鲁棒值最大化问题解的分布示意图Fig.3 Distribution diagram of solutions to the robustness maximization problem

变换预算值C∗时,首先应当确定其取值范围,为此提出如下性质并予以证明.

性质在鲁棒值最大化模型中,成本值上界为

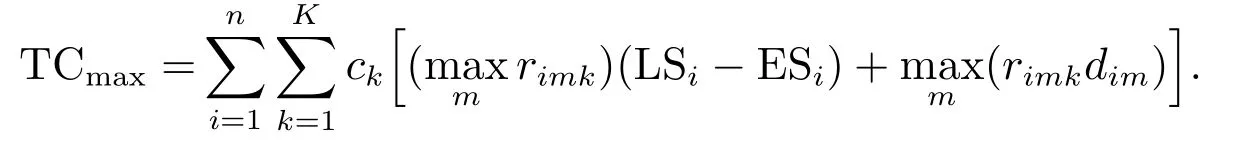
成本值下界为

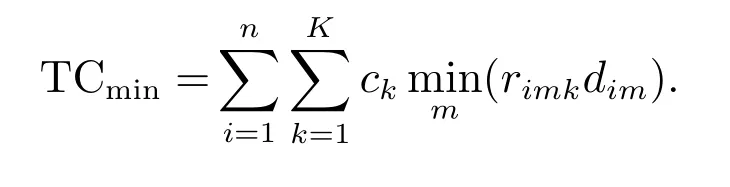
证明

首先变换成本值表示式,进行放大,求其最大值.

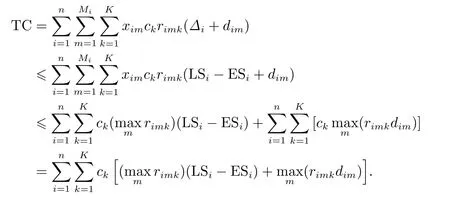
成本值上界的计算式得证.

同样变换成本值表示式,求其最小值.

由于∆i0,则

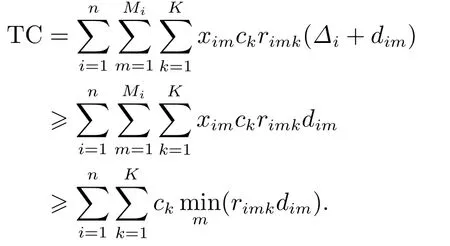
成本值下界的计算式得证.上述性质得证.

由上述性质可知,在成本临界值范围内变化C∗求解鲁棒值最大化子模型可获得多个鲁棒值最大化的解,同时也就得到双目标模型的一系列Pareto最优解.

3 迭代式遗传算法

由于鲁棒性和成本双目标问题的NP-hard属性,本文采用启发式算法求解.遗传算法因其全局搜索能力强,广泛应用于调度优化相关研究中[20−25].在项目调度中,遗传算法可以用于求解给定约束下的单一指标优化问题.但在本文研究问题中,由双目标模型转换后得到的单目标问题需要不断变换预算临界值,在不同的约束下求解鲁棒值最大化问题,反复迭代计算得到多个鲁棒值最大化的满意解,然后剔除支配解、求解得到双目标问题的Pareto 解集.基于上述模型求解需要,设计迭代式遗传算法对预算约束下的鲁棒值最大化模型进行求解.

3.1 解的表示

采用有序活动列表AL和模式列表ML表示进度方案,图4给出一个6个活动的活动列表和模式列表的示例图.

图4 解的表示示例Fig.4 An example of solution presentation

根据模式列表确定项目各活动的执行工期和所需资源量,然后应用SSGS方法将上述活动列表转化为一个可行的进度方案S={s1,s2,...,sn},以及相应的各活动最晚开始时间列表

如前所述,运用SSGS方法得到的进度方案是在满足各项约束下的各活动的最早开始时间.由以上两个进度方案开始时间列表经计算就可以得到各活动的缓冲时间列表{∆1,∆2,...,∆n},然后计算得到进度计划的鲁棒值和成本值.

3.2 算法步骤

迭代式遗传算法包含内外两层循环,内层采用遗传算法基本操作步骤实现给定预算约束下鲁棒值最大化单目标子模型优化,外层计算成本值上下界范围,逐步变换成本临界值并输入到内层,当内层算法计算完成后存储子模型优化最优解,最终剔除支配解获得最优Pareto 解集.

迭代式遗传算法的具体实施步骤如下.

步骤1读入项目网络数据,包括项目活动工期、优先关系、执行成本及资源量等.

步骤2应用模型中的性质计算得到成本值的上下界,将成本值下界作为初始成本临界值应用到内层迭代算法中.

步骤3生成种群规模大小的初始种群,使得每个个体都满足资源约束、优先关系约束以及成本临界值约束.

步骤4计算种群中个体的鲁棒值目标函数,并按照鲁棒值从大到小依次排序.

步骤5依据鲁棒值大小复制精英个体到子代中,并进行交叉操作和变异操作生成满足各类约束的新个体进入子代,形成子代种群.

步骤6判断是否达到最大迭代次数,若是,进入下一步,否则返回步骤4.

步骤7记录当前最优解的鲁棒值和成本值,判断成本临界值是否超过成本值上界,若是,进入下一步,否则增加成本临界值返回步骤3.

步骤8整合所有记录的最优解,剔除非支配解形成Pareto解集并输出,结束算法.

在预算值给定时,鲁棒值最大化单目标问题由内层遗传算法求解,它从外层获取项目网络数据和成本临界值,求解预算约束下的鲁棒值最优进度计划,主要包含生成初始种群、个体排序、复制操作、交叉操作和变异操作五个步骤.逐个生成种群个体的活动列表和模式列表,保留满足工期约束和预算约束个体形成初始种群.计算鲁棒值,按照鲁棒值大小对种群个体排序.根据精英策略按比例复制种群中排序靠前的个体,直接进入下一代种群.交叉操作在种群中随机选择父本和母本进行活动列表交叉(如图5)和模式列表交叉(两点交叉)操作,将新个体加入到下一代种群中.变异操作随机选取种群中个体对活动列表和模式列表进行变异,变异后个体加入到下一代种群中.

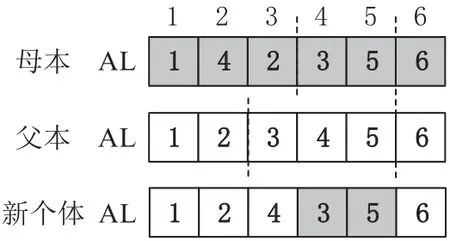
图5 交叉操作示例Fig.5 An example of the crossover operation

应用上述五个步骤,执行若干代,可以得到给定预算约束下的鲁棒值优化的最优解.此外,为求解得到双目标模型的Pareto 最优解集,迭代式遗传算法还实现了如下功能:

1)根据2.4中的性质方法计算成本值上界TCmax和成本值下界TCmin,确定成本临界值变化的范围;

2)按步长变换成本临界值,改变内层鲁棒值优化的约束条件,得到预算约束临界值变化的多个鲁棒值优化解;

3)执行多个鲁棒值优化内层算法,记录相应鲁棒值优化得到的满意解,剔除支配解,得到双目标优化的Pareto解集.

迭代式遗传算法包含内层和外层两部分,内层按照遗传算法的步骤运算获得鲁棒值最大化的最优解,输出给外层,外层计算出成本值的上下界,不断变化,输入到内层进行反复迭代,最终获得鲁棒性和成本双目标权衡的最优Pareto解集.

4 计算实验

为了验证迭代式遗传算法的有效性,应用ProGen[26]在不同参数下生成的360个标准算例对算法进行测试,对比迭代式遗传算法与多重迭代改进算法(Multi-Start Iteration Improvement,MSII),并将计算结果与不考虑预算约束的鲁棒性最大化单目标算法进行比较.变化工期比例和资源比例参数,进行敏感性分析.

4.1 实验设计

计算实验将迭代式遗传算法与多重迭代改进算法进行对比.多重迭代改进算法从一个可行解出发,变化活动列表和模式列表获得邻点,取当前最优解继续迭代,直到达到最大迭代次数输出最优解.然后变换初始可行解继续重复上述迭代步骤,得到多个最优解形成集合,剔除支配解即得到最优Pareto解集.

在对比两个版本算法的求解效果时,需对比算法求解得到的Pareto解集的优劣.由于最优Pareto 解集是未知的,这里用近优的Pareto参考集代替.将迭代式遗传算法运行若干代并将代际种群结合起来形成一个群体,计算得到群体中的所有非支配解即构成参考非支配解集.

定义如下三个参数描述算法计算得到的Pareto解集.

1)平均计算时间ACT

算法计算相同参数下10个算例的平均计算时间,表征算法在计算Pareto前沿时运算的速度,平均计算时间越短说明算法运算速度越快.

2)非支配解集相对于参考非支配解集的收敛度cp

确定第g代种群P(g)中的非支配解集F(g),收敛度指标计算方法如下(进行归一化处理)

其中、分别为参考解集P∗中第k个目标的最大值和最小值.

收敛度值cp越小,说明算法计算得到的Pareto 前沿越接近参考集形成的近优Pareto前沿,计算效果越好,反之则计算效果越差.

3)非支配解集相对于参考非支配解集的分布性dp

首先确定种群P(g)中的非支配解集F(g),将各进度方案成本值区间范围等分成若干个小区间,按照下式计算分布性指标,即

分布性值dp越大,说明算法计算得到的Pareto 前沿上的点分布越均匀,计算效果越好,反之则计算效果越差.

应用ProGen生成标准算例时的参数设置见表1,活动网络规模设置四个水平,项目最大截止日期和资源比例分别设置三个水平,各参数组合下分别生成10 个算例,共得到360个标准算例进行算法测试.

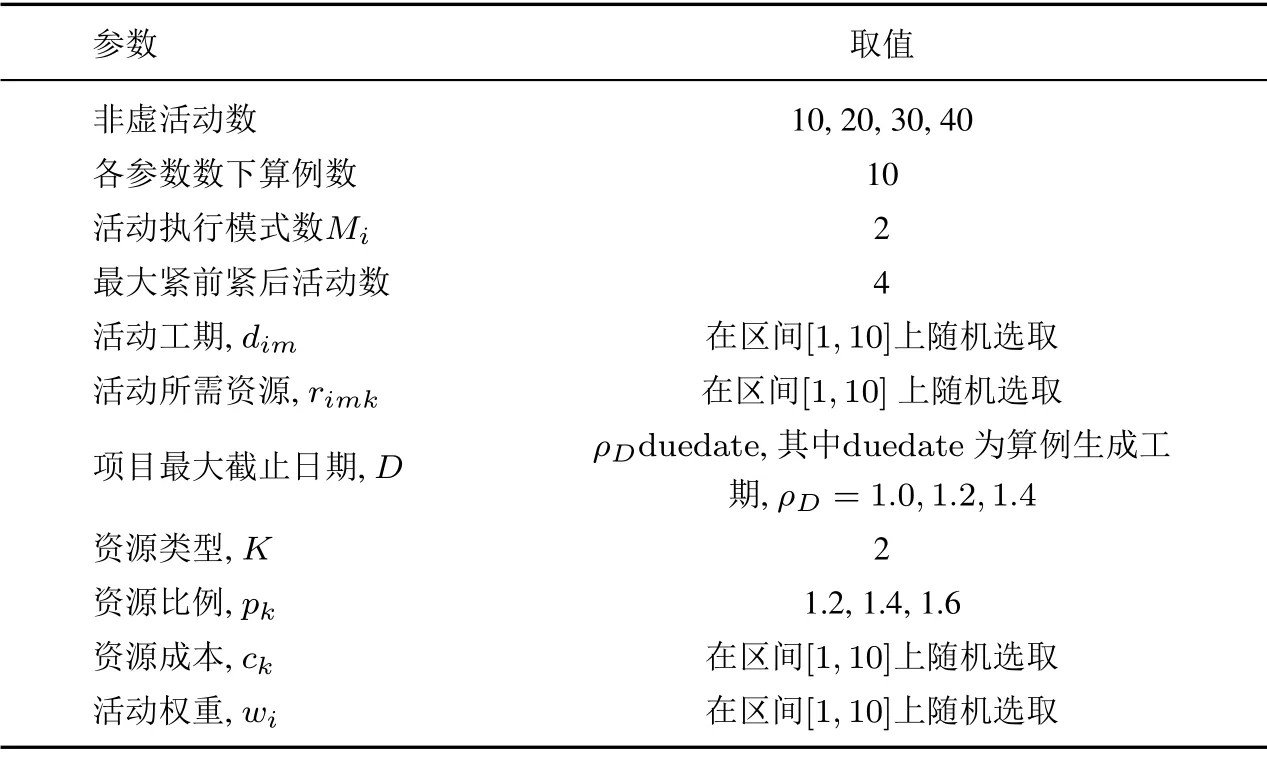
表1 算例参数表Table 1 Parameters of the instances

算法采用Visual Studio 2010中的C++语言编程,在CPU 主频为2.5GHz,内存8GB的个人计算机上运行.将种群规模设置为100,最大迭代次数为100,复制、交叉、变异比例分别为0.2、0.74 和0.06,在给定参数下运算进行求解.

4.2 测试结果

为验证迭代式遗传算法的求解效果,设计多重迭代改进算法进行对比,两个版本算法的测试结果见表2.

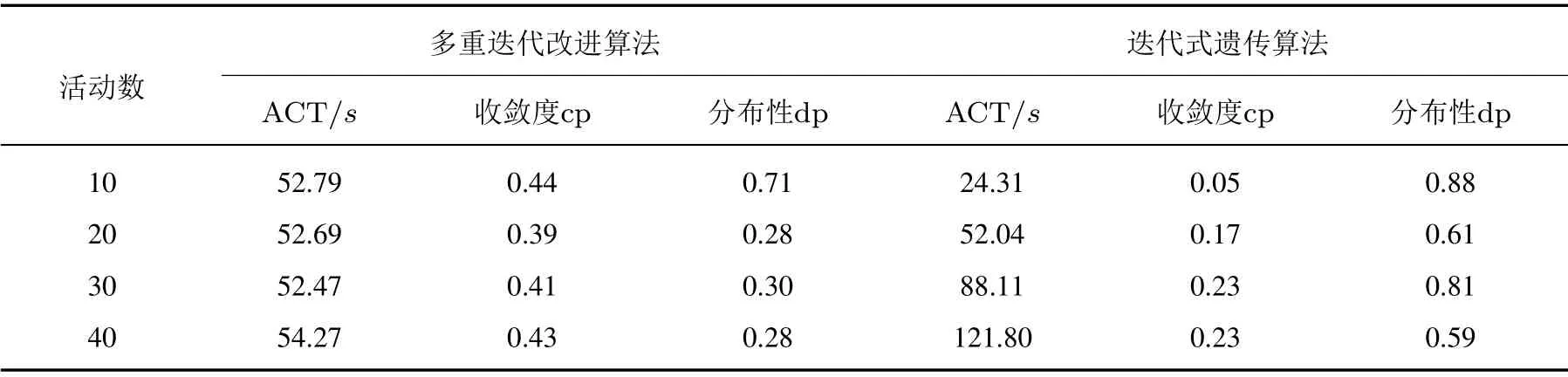
表2 算法测试结果Table 2 Test results of algorithms

从计算时间上看,多重迭代改进算法在不同活动数下差距较小,迭代式遗传算法计算时间随着活动数增加逐渐增大.这是由于迭代式遗传算法需要变换成本值反复执行内外层算法.当活动数逐渐增加时,项目网络变得复杂,成本上下界范围显著增加,内外层算法迭代执行的次数也骤然增加,运算时间变长.

多重迭代改进算法的收敛度在各活动数下均较高,而迭代式遗传算法的收敛度始终较低,算法计算得到的Pareto解集距离最优解集更近.这是由于将双目标模型转化为子模型后,相比于直接在整个解空间中搜索更为有序,效率更高,计算得到的最优解形成的Pareto前沿距离最优前沿更近.

就分布性而言,多重迭代改进算法在各活动下表现都较差.而迭代式遗传算法计算效果明显更好.这是由于鲁棒值最大化子模型中的预算值在上下界范围内逐渐变化、反复求解,相比于双目标的大范围随机搜索更为分散且有方向性,能够有效获得不同预算值下的解,Pareto前沿上的点分布也就更为均匀.

综上,在各活动数下,迭代式遗传算法相比于多重迭代改进算法的收敛度更低、分布性更高,即计算得到的Pareto前沿更接近参考集形成的Pareto 前沿,且Pareto 前沿上的点分布更为均匀.所以,迭代式遗传算法计算效果更好,将双目标模型转化为鲁棒值最大化子模型能够有效求解本文的鲁棒性和成本双目标权衡问题的Pareto 前沿,供决策者在其上进行鲁棒值和成本的权衡,选择鲁棒性大、成本低的进度方案.

4.3 进度方案结果对比

为了更直观地验证迭代式遗传算法的计算效果,对比进度方案优劣,在不考虑成本的条件下实现鲁棒值最大化单目标算法,并计算得到相应进度计划的成本值,将其与Pareto前沿上鲁棒值最大的进度计划进行对比,结果如表3.表中分别给出了两种算法计算得到的鲁棒值最大化进度计划的鲁棒值和成本值,以及鲁棒值最大化算法计算得到的鲁棒值、成本相对于迭代式遗传算法的增量.

表3中,在各活动数下,应用迭代式遗传算法得到最大鲁棒值与鲁棒值最大化算法计算得到的最优解十分接近.在鲁棒值总体差别不大的情况下,各活动数下迭代式遗传算法计算得到的进度方案成本值更小.这是因为我们在模型中考虑了鲁棒性成本,进行鲁棒值和成本的双目标权衡,有效选择出鲁棒值大、成本小的进度方案.也就是说,迭代式遗传算法可以计算得到更低成本的进度计划,在保证项目进度计划鲁棒性的同时降低了项目成本,得到了更优的进度方案.

表3 鲁棒值最大化对比结果Table 3 Comparable results of robustness maximization

4.4 敏感性分析

为分析项目最大截止日期和资源可用量对项目鲁棒值和成本的影响,保持其他参数不变,分别变化工期比例ρD和资源比例pk,运行迭代式遗传算法求解相应鲁棒值和成本值,计算结果如表4.

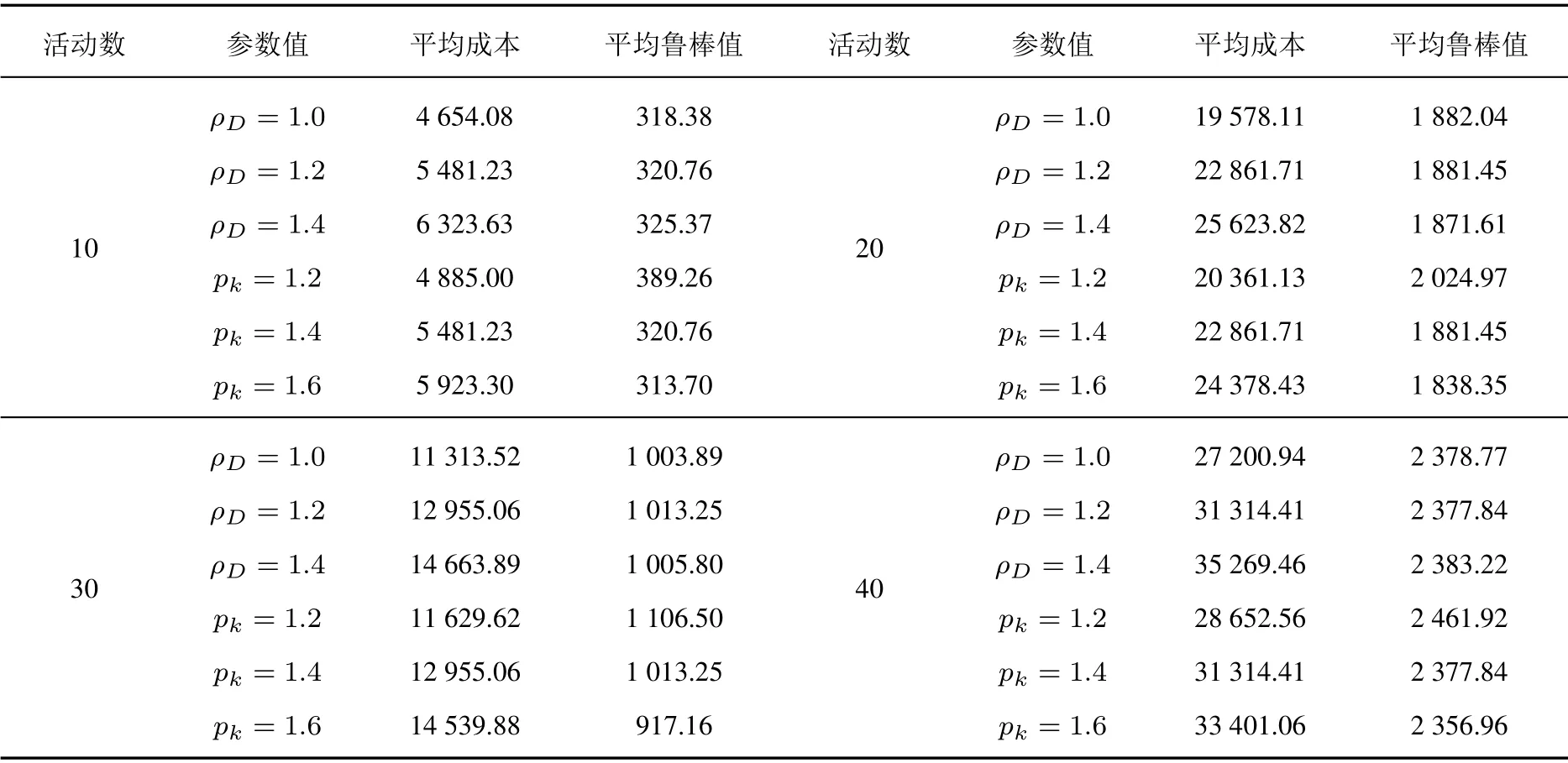
表4 敏感性分析结果Table 4 Results of sensitivity analysis

根据表4分别绘制鲁棒值、成本随工期比例和资源比例变化趋势图,如图6∼图9所示.观察图6,在不同活动数下,平均成本都随着工期比例的增大而增大,工期延长使得项目占用资源的总时间变长从而造成成本增加.图7显示工期延长后,平均鲁棒值几乎不发生变化,说明当前资源已被充分利用,即使增加项目工期也没有多余资源可以为活动添加有效的缓冲时间,无法提升项目鲁棒值.由此说明,在资源已经得到充分利用时,增大项目最大截止工期非但不能有效提升项目鲁棒值,反而会显著增加项目成本,这对管理者而言是一种得不偿失的举措,特别是活动繁多的复杂项目,为防止成本过度消耗要注意避免增加工期比例参数.

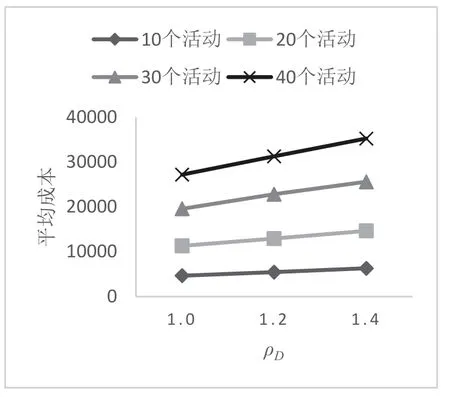
图6 工期比例对成本的影响Fig.6 The impact of the duration ratio on the cost

图7 工期比例对鲁棒值的影响Fig.7 The impact of the duration ratio on the robustness

观察图8、图9,当资源比例逐渐增大时,在各活动数下平均成本均明显增大,但是平均鲁棒值却无明显变化,即在当前参数条件下,增加资源投入会使得项目成本增加,对鲁棒值无明显影响.资源已经十分充足,再增加额外的资源只会增加成本,对鲁棒性提升也毫无用处,这也是管理者应当避免的举措.

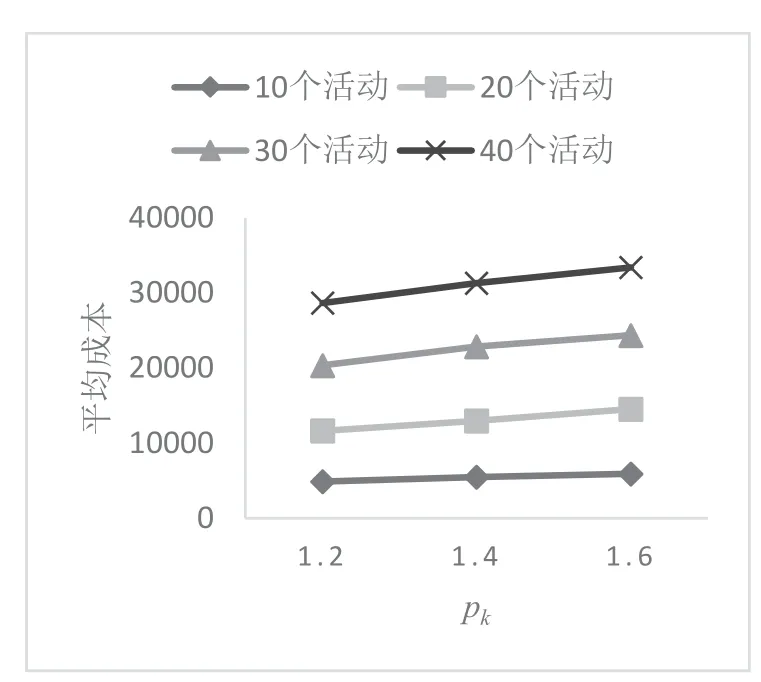
图8 资源比例对成本的影响Fig.8 The impact of the resource ratio on the cost

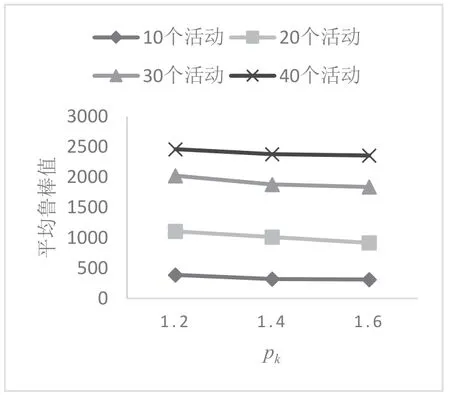
图9 资源比例对鲁棒值的影响Fig.9 The impact of the resource ratio on the robustness

5 结束语

本文从项目调度现实情况出发,在不确定环境下进行鲁棒性和成本的双目标权衡.构建鲁棒性和成本双目标优化模型,最大化项目鲁棒值的同时最小化项目成本,将双目标模型转换为预算约束下的鲁棒值最大化子模型,并提出性质求解成本值上界和下界.考虑到问题的NP-hard属性,设计了迭代式遗传算法,并将计算成本值上下界的性质应用到算法迭代进程中.为验证算法的有效性展开大规模算法测试,进行算法对比.最后,通过敏感性分析得到相应的管理启示.本文的研究可为管理者制定具有稳定性的进度计划提供决策支持,便于对进度方案的鲁棒性和成本进行权衡.需要指出的是,鲁棒性的表示方法并不唯一,在后续研究中可以应用其他指标表示项目鲁棒性,使鲁棒值更能代表进度计划执行时的鲁棒性.