基于机器学习的切丝后含水率预测及控制方法

高立秀 陈得丽 万兴淼 王星皓 朱知元 李永华 佘 迪 孔维熙

(红云红河烟草〔集团〕有限责任公司曲靖卷烟厂，云南 曲靖 655001)

切丝后含水率是烟叶制丝生产环节的一项重要工艺指标，其符合性和稳定性对后续工序过程的稳定控制具有重要作用。目前，中国烟叶制丝线主要通过人工倒推估算润叶加料出口含水率和松散回潮出口含水率以实现切后含水率的控制。由于影响切丝后含水率的因素较多，如环境温湿度、贮叶时间及部分人为操作习惯等，简单估算无法实现前后工序参数协同和精准控制。钟文焱等[1]提出了一种利用多元回归分析计算松散回潮机回潮加水比例，实现烘丝含水率控制的方法，但该方法的模型解释度不高，仅考虑了车间环境温湿度和贮叶时间，未涉及其他影响变量。李贵川等[2]通过设定环境温湿度T、空气相对湿度R、生产设备海拔高度H，其在卷烟加工过程中保持恒定不变，测量各节点烟丝水分重量百分比值，计算各工序卷烟水分变化值，从而确定烘丝入口水分设定值。

制丝车间松散回潮工序至切丝工序的工艺流程如图1所示，试验拟将切丝前工序分离，采取“分段建模在先，串联预测在后”的方式建立数学模型。其中，分段建模包括：① 投料段模型(水分仪1至水分仪3)，使用XGBoost模型建模预测；② 车间温湿度预测模型，使用SARIMAX模型预测未来数小时车间环境温湿度；③ 切丝段模型(水分仪3至水分仪4)，使用神经网络模型建模，蒙特卡洛仿真进行预测。旨在提高切丝后含水率的稳定性与符合性，为下一步的烘丝工序和掺配加香工序的平稳控制提供依据。

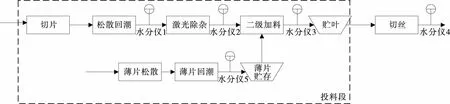
图1 工艺流程图

1 数据预处理

1.1 数据样本筛选及清洗

从制造执行系统(MES)中提取2020年3月1日—6月27日云烟(A)牌号生产的448批次稳态数据，包含16个特征变量，其中，松散回潮出口含水率、松散回潮片区温度、松散回潮片区湿度、润叶加料工艺流量、加料流量、润叶加料片区温度、润叶加料片区湿度、润叶加料出口温度、薄片含水率、薄片掺加流量、润叶加料机蒸汽添加值、润叶加料出口含水率属于投料段模型变量；润叶加料出口含水率、贮叶时间、切丝片区温度、切丝片区湿度、切丝后含水率属于切丝段模型变量。对原始数据进行有效数据筛选：对缺失值使用热卡填补法填充[3]，对异常值进行3σ原则识别并剔除，对松散回潮出口含水率标准偏差、润叶加料出口含水率满足能力(CP)、切丝后含水率过程能力指数(CPK)不满足工艺考核标准的数据进行剔除。从时序数据库提取2019年6月27日—2020年6月27日10～23点的温湿度的时序数据，并进行间隔1 h的采样作为温湿度的历史数据，使用采集时的日期和时间作为数据序号。

1.2 数据标准化处理

数据需除去量纲的影响以描述客观规律，选择Z-score 标准化方法，按式(1)对所有数据进行标准化。

(1)

式中：

x——原始数据；

μ——样本均值；

σ——样本方差。

2 特征构造及特征选择

使用Anconda3-5.1开发环境和Python 3.6.3 实现代码[4]。数据预处理完成后，需选择有意义的变量输入模型进行训练。原始特征变量中的湿度均是相对湿度，即当前湿空气中水蒸气内分压力和相同温度下饱和湿空气内水蒸气分压力的比值，根据干燥理论，物料水分散失主要与湿空气中的水蒸气分压有关，而且空气中的温度和相对湿度是两个相互影响的变量，因此按式(2)～式(4)计算湿空气的焓值[5]，去除变量的交互性。

I=(1.01+1.88H)T+2 491H,

(2)

(3)

(4)

式中：

I——湿空气的焓值，kJ/kg；

H——空气中的湿含量，kg水/kg干空气；

RH——相对湿度，%；

PV——湿空气的饱和压力，Pa；

T——湿空气的温度，℃。

由式(2)构造出两个新的变量：松散回潮片区湿空气的焓值和润叶加料片区湿空气的焓值，故投料段模型共包括14个特征变量。通过递归特征消除法(RFE)[6]剔除冗余的特征，提高模型精确度，减少运行时间。选取树模型作为基准模型，通过反复构建基准模型，选出影响最大的变量并重复该过程，直至遍历所有变量。投料段13个输入变量经递归特征消除法后的影响系数见表1。

由表1可知，经递归特征消除法(RFE)计算后，剔除冗余的特征：松散回潮片区温度、松散回潮片区湿度、润叶加料片区温度、润叶加料片区湿度、薄片掺加流量。最终的投料段模型的输入变量(经标准化后)见表2。

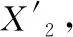
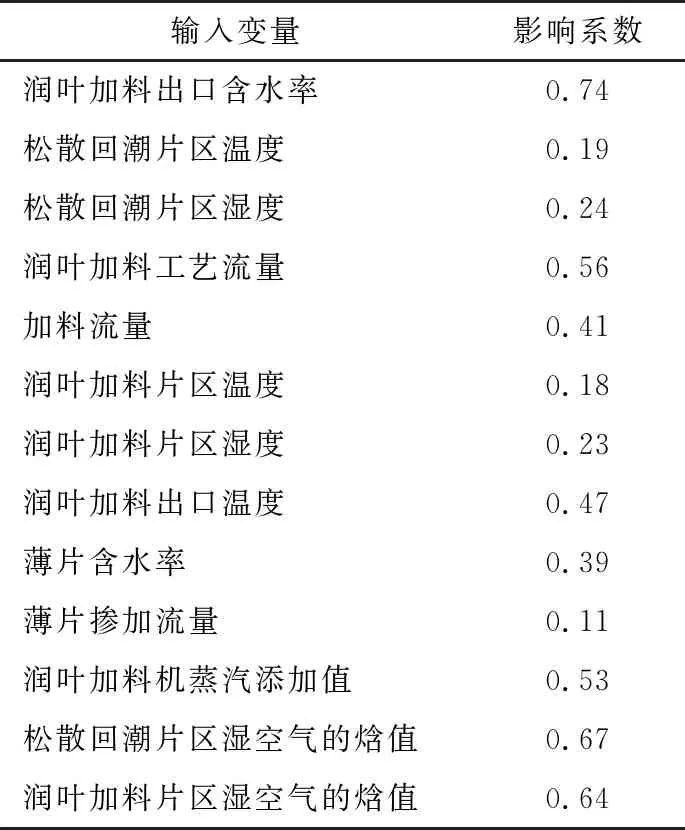
表1 投料段输入变量的影响系数表

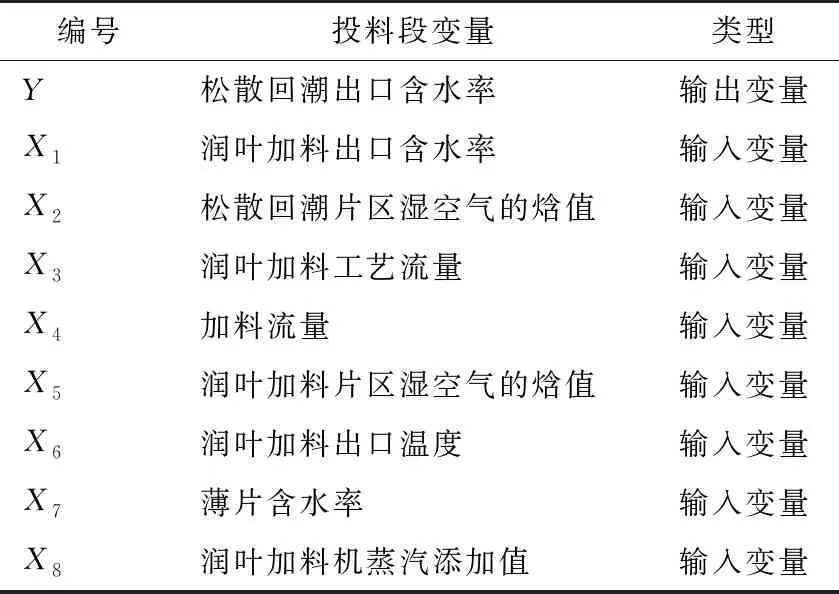
表2 投料段模型的变量

(5)

(6)

(7)

切丝段模型的最终变量定义及选择见表3。

3 模型构建

3.1 投料段XGBoost模型构建及预测

集成学习是指将几种机器学习技术组合成一个预测模型的元算法，可以有效提升预测效果。集合方法通常分为bagging和boosting两种，前者主要用于降低方差，后者主要用于降低偏差，文中建立投料段预测模型需最大程度减小预测偏差，所以选用boosting集成方法。其中GBDT算法[7]是boosting方法的代表之一，XGBoost算法[7-8]是在GBDT算法基础上进行改进，不仅实现了并行近似直方图算法以高效生成分割点，并通过正则化项解决了GBDT的过拟合问题，其准确度高、不易过拟合、可扩展性强。

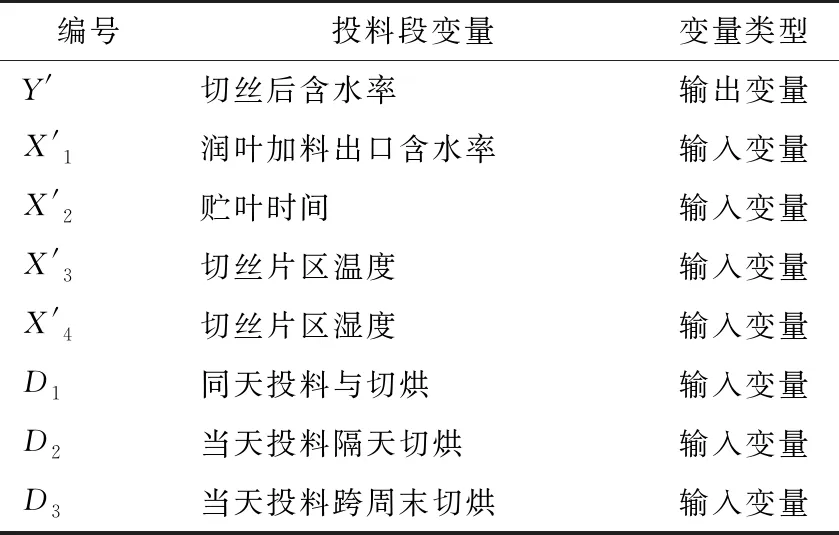
表3 切丝段模型的变量

因此，选用XGBoost算法构建投料段模型，并直接预测松散回潮出口含水率Y。XGBoost模型经贝叶斯调参进行模型参数优化后，得到模型的树个数为130棵，树的最大深度为7，最小叶子节点样本权重和为4，节点分裂所需的最小损失函数下降值gamma为0.01，随机采样比例subsample为0.8，有效防止过拟合和欠拟合。模型预测效果验证标准为松散回潮出口含水率预测值误差在±0.2%，判定为预测准确，预测效果优。

投料段XGBoost模型预测效果见图2。由图2可知，松散回潮出口含水率预测值和实际值曲线吻合度较高，模型得分为92.37，均方误差MSE为0.005，且预测结果误差均控制在0.3%内，预测准确率(误差在±0.2%内)为86.49%，预测效果优。

3.2 温湿度SARIMAX模型构建

物料完成润叶加料工序后，需经过4～72 h贮叶才进行切丝，即润叶加料出口含水率是“现在值”，切丝片区环境温湿度和切丝后含水率属于“未来值”。作为切丝段神经网络模型输入变量的切丝片区温湿度是当前不能确定的变量。所以在使用神经网络模型对切丝出口水分进行预测前，需对切丝片区温湿度变量进行预测。选择SARIMAX对环境温湿度进行预测[9-11]，建立湿度预测SARIMAX(1,1,1)×(0,1,1,14)模型，湿度模型中AR为0.467 5,MA为-0.703 4,SMA为-0.942 6；温度模型为SARIMAX(0,1,1)×(1,1,1,14)，温度模型中MA为-0.196 6,AR为0.334 5,SMA为-0.908 8。

湿度、温度预测模型分别如式(8)、式(9)所示。

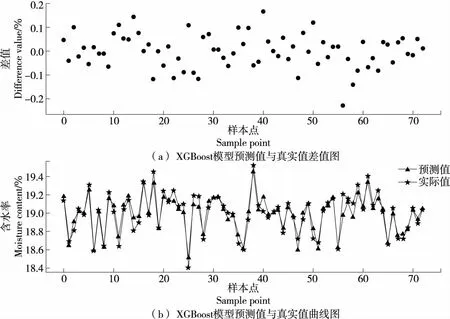
图2 XGBoost模型预测效果

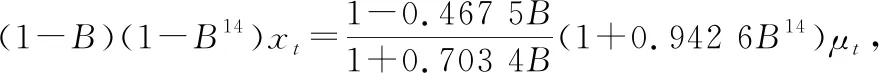
(8)

(9)

式中：

xt——温度或湿度的时间序列；

μt——随机成分；

B——移动算子。

温湿度模型预测结果见图3。由图3可知，温湿度模型的预测得分分别为88.12，87.49，MES分别为0.16，0.28，预测值和实际值吻合度较高。

3.3 切丝段神经网络模型构建和蒙特卡洛求解

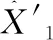
图3 温湿度模型预测结果

模型预测效果准确的标准为切丝后含水率实际值与期望值的误差在±0.15%内，同时实际切丝后含水率CPK≥1.33，预测效果优。神经网络预测效果见图4。由图4可知，切丝后含水率预测值和实际值曲线吻合度较高，训练集模型得分为96.81，测试集模型得分为90.36，均方误差为0.02；测试集预测结果误差控制在±0.15%以内，模型预测效果优。

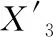
4 模型应用及效果

通过预先构建3种预测模型，在满足切丝后含水率预测值与工艺标准值误差最小这一控制条件下，对润叶加料及松散回潮两个工序的物料含水率进行预测，保证切丝后含水率的稳定性与符合性。其中润叶加料出口的含水预测最优值可以直接作为输入变量用于松散回潮出口含水率的预测中，而松散回潮出口的含水率可以直接作为松散回潮智能控制系统的目标值，由此在控制物料含水率的同时解决了松散回潮出口含水率、润叶加料出口含水率和切丝后含水率之间的质量指标关联匹配问题。切丝后含水率预测及控制流程图如图6所示。

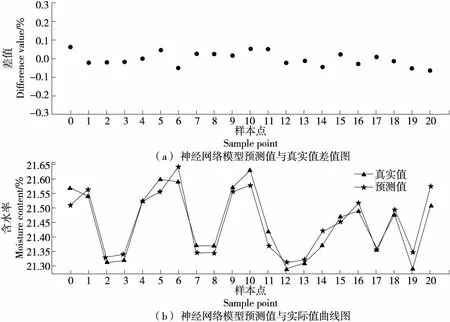
图4 神经网络模型预测效果

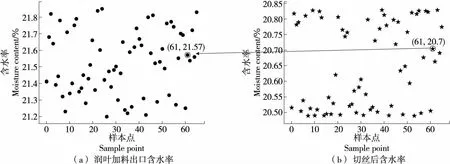
图5 蒙特卡洛仿真映射图

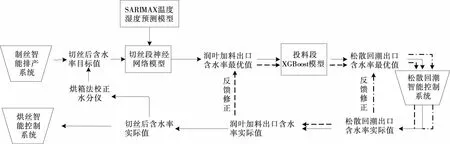
图6 切丝后含水率预测及控制流程图

云烟(A)牌号从2020年7月1日起应用切丝后含水率预测模型指导实际生产，2020年7月1日—9月30日共生产185批，切丝后含水率实际值与标准值之间的误差分布情况见表4。对比2019年同期，其预测误差在±0.15内(改进前占比为62.57%，改进后占比达83.24%)。

切丝含水率CPK分布情况见表5。由表5可知，切丝含水率CPK达标合格率改进前为91.44%，改进后为97.30%，提升了5.86%，有效保证了后续工序的加工稳定性。

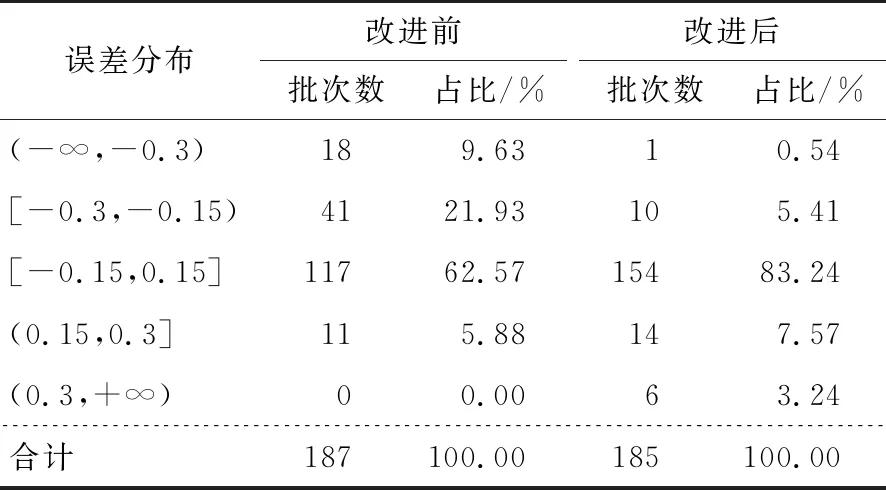
表4 云烟(A)牌号切丝后含水率误差分布

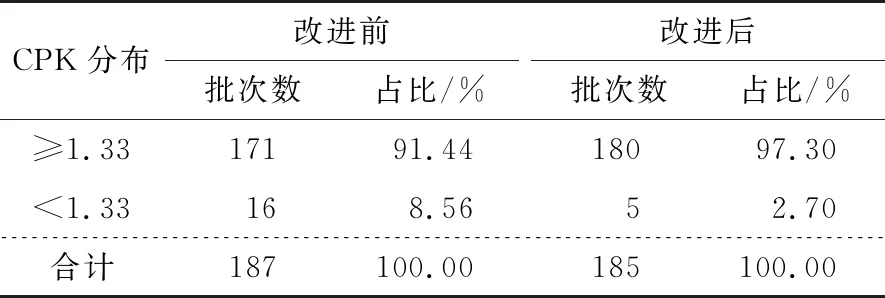
表5 云烟(A)牌号切丝含水率CPK分布

5 结论

通过构建投料段XGBoost模型、温湿度SARIMAX预测模型、切丝段神经网络模型，将预测的润叶加料出口含水率最优值直接用于松散回潮出口含水率的预测，松散回潮出口含水率预测最优值可作为智能加水控制系统的目标值，由此在控制物料含水率的同时解决了松散回潮、润叶加料和切丝工序的指标关联匹配问题。仿真结果表明，云烟(A)牌号切丝后含水率的准确率提升至83.24%，切丝后含水率CPK合格率提升至97.30%，说明模型预测效果较好。同时模型适用于其他牌号卷烟水分控制，可通过进一步优化模型参数，从而提升切丝后含水率的控制精度。试验模型仍存在一定的提升空间及改善之处，如当生产计划临时改变以及天气骤变导致算法学习的历史数据无法快速更新，其预测会存在一定误差。