金属孔阵列电极板间大气压等离子体的微波传输特性
2021-05-10褚佳琪徐金洲朱芸桢
褚佳琪,徐金洲,朱芸桢
(东华大学 理学院, 上海 201620)
大气压放电等离子体具有低温、高活性粒子浓度、低污染等特点,在生物医学[1]和环境治理[2]等领域发挥着重要作用。射频大气压辉光放电等离子体放电装置(见图1)使用穿孔的平行电极板,通过射频电源激励在核心区产生大面积具有高活性粒子浓度的容性耦合等离子体。这些等离子体被广泛应用于薄膜沉积[3]和材料表面改性[4]研究。等离子体放电装置的电极结构可被看作两层平行的金属孔阵列结构。亚波长的金属孔阵列结构可产生表面等离激元[5-7],其被认为是引发传输特性中异常透射现象的原因,引起了学者们的广泛关注。Miyamaru等[8]研究了太赫兹波通过两层金属孔阵列的异常传输并解释为表面波间的近场耦合,而Sakai等[9]、Lee等[10]进一步研究了电磁波通过金属孔阵列和微等离子体复合结构的传输特性,将表面等离激元与等离子体结合实现了宏观介电常数的动态控制。

图1 射频大气压辉光放电等离子体放电装置示意图Fig.1 Schematic of the radio frequency atmospheric pressure glow discharge plasma device
迄今为止,应用比较成熟的等离子体诊断方法包括光谱法、探针法和微波法。针对射频辉光放电等离子体,Xu等[11]通过仿真模拟对高气压条件下的微波共振探针诊断法进行研究,提出根据反射谱中共振峰的半高宽计算等离子体参数的方法;严威[12]对余辉区进行试验测量,估算等离子体密度约为1015m-3,但是发现探针易受金属放电装置的干扰,导致灵敏度降低。同时,大气压下放电间距很小,探针无法浸入核心区中来诊断等离子体。因此,微波法成为一种可行的诊断方法。常用的微波法为微波干涉法,如Lu等[13]使用105 GHz毫米波干涉仪系统测量大气压氦等离子体,估算得出余辉区等离子体密度为8×1018m-3。
本文对微波反射法用于诊断射频大气压辉光放电核心区的可行性进行探索。考虑到入射微波与金属孔阵列结构相互作用会产生表面等离激元共振模式,对微波通过金属孔阵列结构和通过存在等离子体的金属孔阵列电极结构2种情况进行仿真模拟,研究电极厚度、放电间距等结构参数和等离子体参数对微波传输特性的影响,并根据反射频谱和对应的电磁场分布情况分析共振模式的特性。
1 仿真模型
本文使用COMSOL软件进行仿真研究。双层金属孔阵列电极结构的仿真模型如图2所示,金属孔的形状为方孔结构,具体的结构参数包括结构单元的周期p(5 mm)、方孔边长a(2 mm)、电极厚度h和电极间距d。设置Floquet周期性边界条件并将其应用于xz和yz平面的4个边界,入射微波(横磁波)垂直于xy平面,金属材料设置为理想导体。
2 耦合谐振理论
边长为2 mm的方孔对应的截止频率为75 GHz,当工作频率小于截止频率时,金属孔阵列可被视为具有等效负介电常数的均匀介质[7],此时双层金属孔阵列电极结构的表面可等效为4个表面波谐振器,通过倏逝场激发并产生耦合的表面等离激元共振模式[14]。表面波谐振器之间的耦合[15-16]可描述为
(1)
(2)
(3)
(4)
式中:ψi(τ)=Εie-iντ(i=1, 2, 3, 4),表示各个表面波谐振器的电场;τ=ωrest和ν=ω/ωres分别为无量纲的时间和频率,ωres为谐振器共振时的本征频率;Q-1为谐振器中的损耗;q0为单层金属孔阵列上下表面之间的耦合系数;q1为两层金属孔阵列之间的耦合系数;F0为入射场的有效激励振幅。方程的稳态解Εi(i=1, 2, 3, 4)由式(5)~(8)得出。
(5)
(6)
(7)
(8)

特别地,对于单层金属孔阵列结构,q1=0,则方程式(5)~(8)可简化为
(9)
(10)
该理论模型通过损耗Q-1、耦合系数q0和q1解释耦合模式的共振特性和空间场分布特征。根据微波通过单层或双层金属孔阵列结构传输的仿真结果,依据入射微波的反射频谱确定共振条件。
3 结果与分析
3.1 金属孔阵列电极结构对微波传输特性的影响
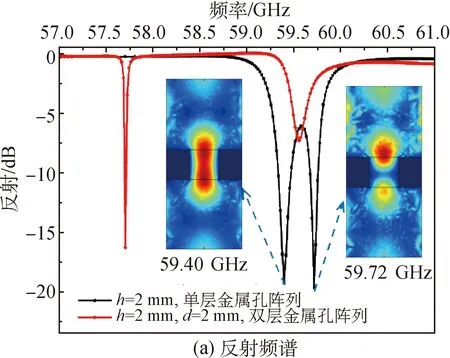
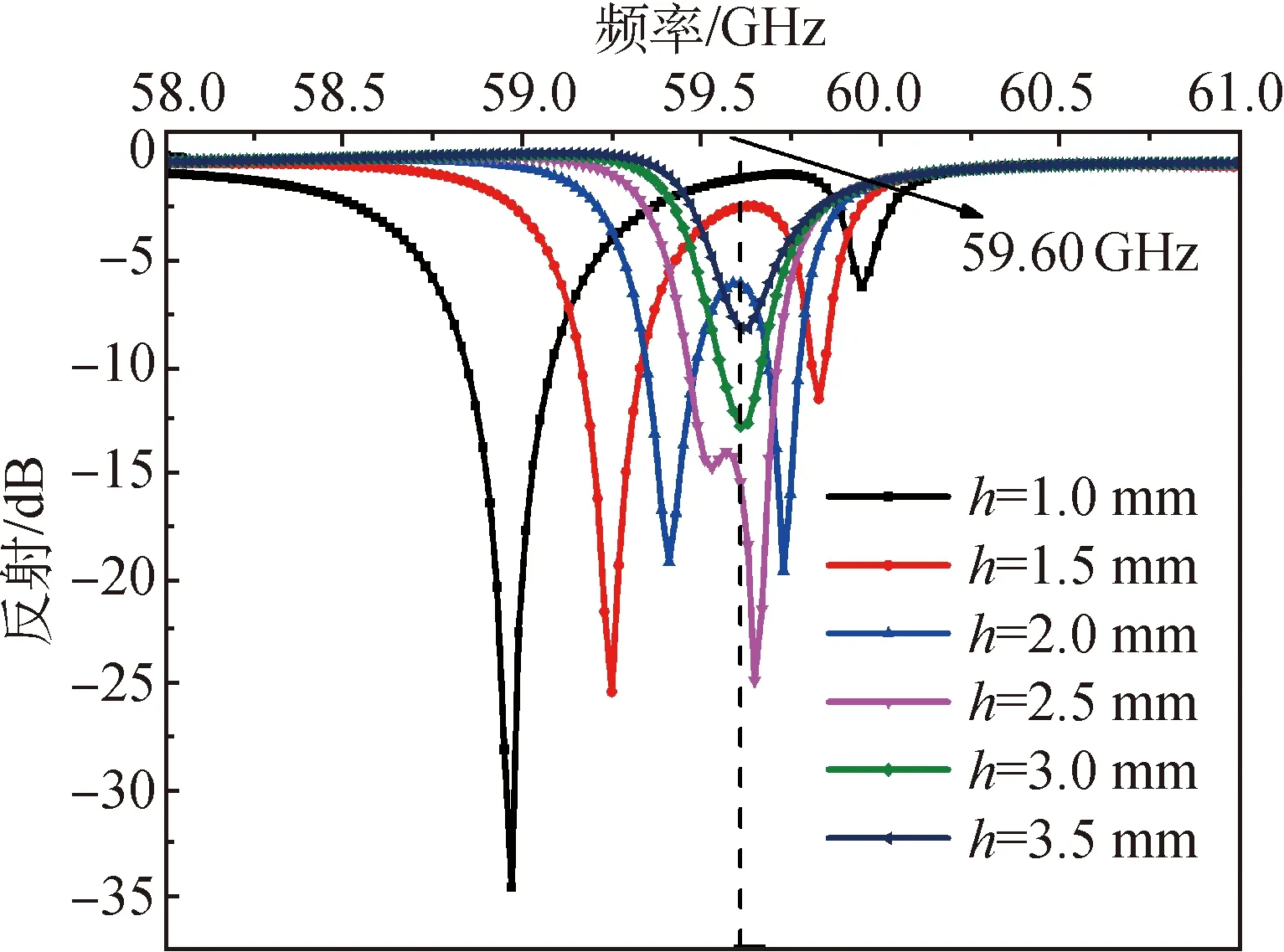
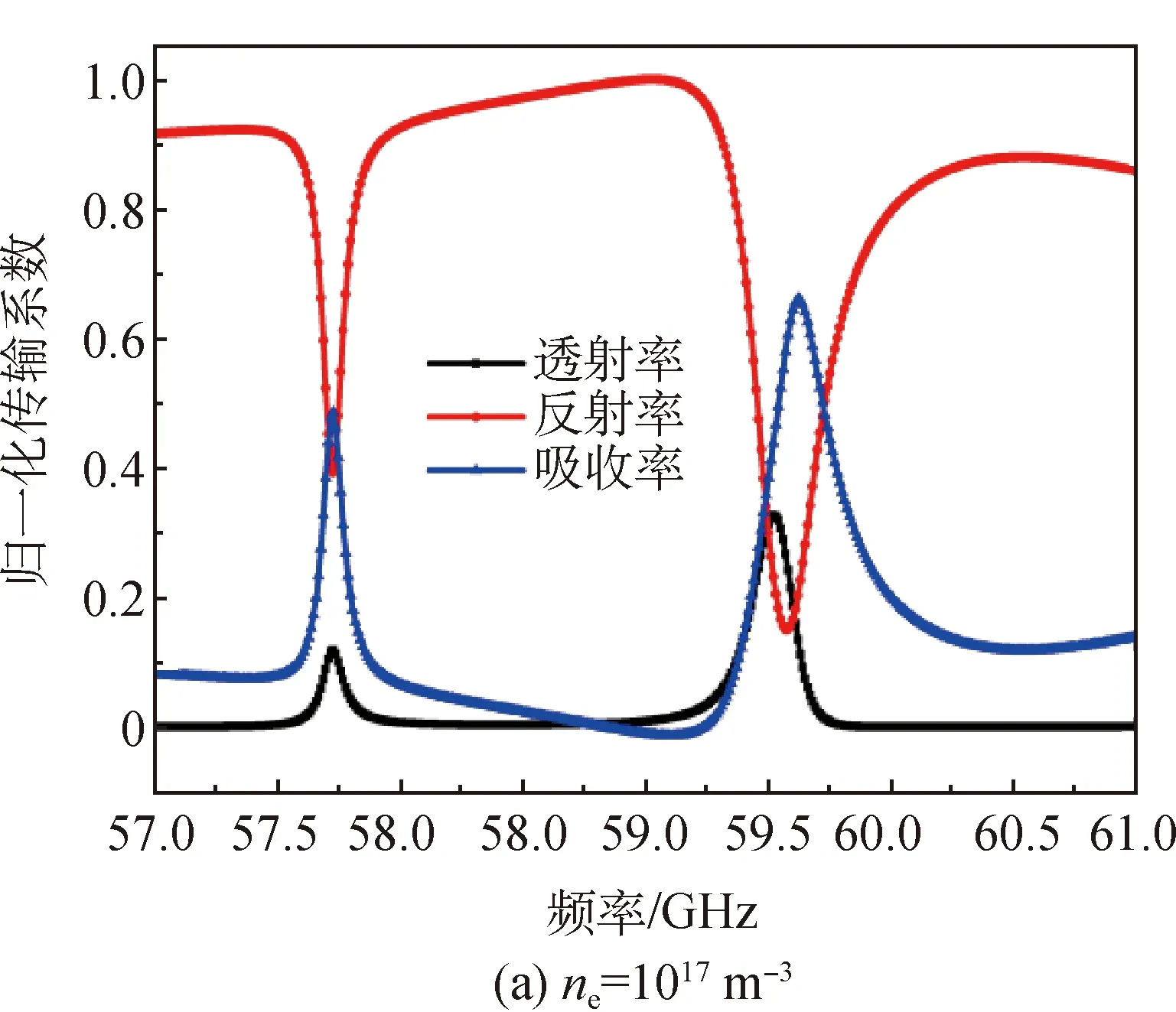
在57~61 GHz内,微波垂直入射双层金属孔阵列电极结构的反射频谱和归一化传输系数如图3所示,其中h=2 mm,d=2 mm。由图3(a)可知,反射频谱存在2个明显的共振峰,共振频率分别为57.70和59.56 GHz。虽然根据耦合谐振理论很难得到耦合模式对应共振频率的解析式,但可通过赋值法使用MATLAB软件绘制|Ei|曲线来分析耦合系数对耦合模式的影响。选择适当的数值代入Q-1、q0、q1,结果表明,仅在q1 图3 微波通过双层金属孔阵列电极结构的反射频谱和归一化传输系数Fig.3 Reflection spectra and normalized transmission coefficients of microwave through double-layer metal hole array electrode structure 为深入分析电极结构对金属孔阵列电极结构中微波传输特性的影响,仿真研究h=2 mm时单层金属孔阵列的微波传输特性,微波通过单层金属孔阵列结构的反射频谱和归一化传输系数如图4所示。由图4(a)可知,反射频谱中有2个频率非常接近的共振峰,分别为59.40和59.72 GHz,定义为耦合模式Ⅰ′和耦合模式Ⅱ′。此外,双层金属孔阵列的反射谱中耦合模式Ⅱ位于单层金属孔阵列结构的2个共振频率之间,表明耦合模式Ⅰ的出现是由于双层金属孔阵列电极结构之间的耦合。图4(a)插图为单层金属孔阵列于共振频率处yz截面的电场分布,可以看出,耦合模式Ⅰ′处电场呈对称分布,而耦合模式Ⅱ′处电场集中在入射波侧的谐振器中,这与图3(a)插图中的分布情况类似。由图4(b)可知:耦合模式Ⅰ′的入射能量表现为高传输,其中微波通过金属孔阵列的透射率达80%,而计算所得金属孔的占空比为16%,透射率远大于占空比,这被称为异常透射现象;耦合模式Ⅱ′的能量表现为较高的存储或损耗。图3和图4表明,微波与单层或双层金属孔阵列结构相互作用产生的耦合模式具有共性特征。 图4 微波通过单层金属孔阵列结构的反射频谱和归一化传输系数Fig.4 Reflectance spectra and normalized transmission coefficients of microwave through single-layer metal hole array structure 单层金属孔阵列结构中微波传输特性随电极厚度的变化情况如图5所示。反射频谱的变化主要表现在双耦合模式对应的共振频率漂移和反射变化两方面。由图5可知,随电极厚度的增加,2个共振峰均向频率59.60 GHz处偏移,且当h≥3.0 mm时,2个共振峰合并为1个。出现频率漂移现象的原因是电极厚度的增加导致耦合系数q0降低。根据耦合谐振理论,通过MATLAB软件绘制|E′i|曲线发现,降低耦合系数将促使2个共振频率相互靠近,当电极厚度过大而无法发生耦合时,只有1个共振峰,并且仿真所得反射频谱的结果与理论分析结果基本吻合。当电极厚度变化时,两种耦合模式的反射表现出明显相反的响应。对于耦合模式Ⅰ′,反射随电极厚度的增加而增加;对于耦合模式Ⅱ′,反射随电极厚度的增加而减小。这可能是由于低频模式对应纵向的高传输,而高频模式对应横向的存储或者损耗,二者特性相反造成对表面电场的束缚能力不同。 图5 单层金属孔阵列结构不同电极厚度的反射频谱Fig.5 Reflectance spectra of single-layer metal hole array with different electrode thickness 双层金属孔阵列结构不同电极间距的反射频谱和耦合模式Ⅰ对应的电场分量Ez的分布如图6所示。从耦合模式对应的共振频率漂移和反射变化两方面进行分析。 图6 双层金属孔阵列结构不同电极间距的反射频谱和耦合模式Ⅰ对应的电场分量Ez的分布Fig.6 Reflectance spectra and electric field Ez distributions at coupled mode I of double-layer metal hole array with different electrode spacing 由图6(a)可知,随电极间距的增大,耦合模式Ⅰ的共振频率向59.60 GHz处漂移,与图5中的变化情况类似,这可能是由双层金属孔阵列结构之间的耦合系数q1减小所引起的。但是,耦合模式Ⅱ的共振频率几乎未发生变化,这说明耦合模式Ⅱ受耦合系数q1的影响非常小。此外,耦合模式Ⅱ的反射对电极间距d的变化也不敏感。由图6(b)可知,电极间距的增大会减弱双层金属孔阵列电极结构之间的耦合效应。 基于上述耦合模式的基本特性,研究等离子体对微波传输特性的影响。辉光放电等离子体通过射频电源激励于核心区产生,然后在气流作用下进入微波入射侧的金属孔中,见图1。因此,仿真模拟中将等离子体设置在双层金属孔阵列的放电核心区和微波入射侧的金属孔中。大气压氦气等离子体可被视为具有相对介电常数εp的均匀介质,可采用Drude模型表示,如式(11)所示。 (11) 微波通过存在等离子体的两层平行金属孔阵列电极结构传输时,等离子体密度ne对反射频谱的影响如图7所示。仿真条件设置为大气压p=1.013×105Pa,电子温度Te=1 eV。大气压下鞘层厚度的影响可忽略不计。由图7可知,当等离子体密度改变时,两种耦合模式对应的共振频率均未出现明显的漂移现象,表明等离子体对双层金属孔阵列电极结构间的耦合系数q0和q1的影响很小,但存在损耗Q-1。因此,本节主要关注共振模式对应的反射变化。随等离子体密度的增加,耦合模式Ⅰ对应的反射逐渐增大,当ne≥1018m-3时共振峰消失,但耦合模式Ⅱ表现出相反的响应,其对应的反射值逐渐减小。这与两种耦合模式对应于不同的传输特性是相符的。 图7 不同等离子体密度下的反射频谱对比图Fig.7 Comparison of reflection spectra at different plasma densities 不同等离子体密度对应的归一化传输系数和总能量损耗密度的分布如图8所示。对比图8(a)和(b)可知,随着等离子体密度的增加,耦合模式Ⅰ的反射率增大、透射率减小,耦合模式Ⅱ的反射率减小、吸收率增大,甚至在ne=1019m-3处出现全吸收现象。大气压碰撞等离子体会引起能量耗散,由图8(c)可知:当ne=1017m-3时,耦合模式Ⅰ处微波通过金属孔内的等离子体进入核心区产生损耗,而耦合模式Ⅱ处的损耗则主要发生在微波入射侧金属孔内的等离子体;耦合模式Ⅱ在ne为1017、1018和1019m-3时,等离子体密度越高,损耗越强。 图8 不同等离子体密度对应的归一化传输系数和总能量损耗密度的分布Fig.8 Normalized transmission coefficient and distribution of total power dissipation density at different plasma densities 反射频谱中耦合模式Ⅱ的品质因子Q与空气中的品质因子Q0的比值随等离子体密度的变化如图9所示,仿真压强分别为7.999×104和1.013×105Pa。 图9 模式Ⅱ的品质因子Q与空气中品质因子Q0的比值与等离子体密度的关系Fig.9 Dependence of the ratio of quality factor Q at mode IIto the one Q0 in air on plasma density 由图9可知,Q/Q0值随等离子体密度的增大而增大。理论上,等离子体密度增大意味着损耗变大,这将导致反射频谱共振对应的品质因子降低,正如耦合模式Ⅰ的变化。但笔者发现耦合的表面等离激元共振模式Ⅱ却表现出完全相反的特性,这种模式上的差异为通过试验测量微波反射频谱并将其应用于核心区等离子体的诊断提供了一种新方法。而压强对Q/Q0值的影响很小,因此上述规律适用于高压等离子体诊断。当等离子体密度高于某一临界值时,Q/Q0值快速减小,这是因为高稠密的等离子体会导致微波入射到金属孔中的能量减小。Moravej等[3]估计射频大气压辉光放电核心区的等离子体密度约为1018m-3量级,本文仿真结果发现,微波的传输特性在高等离子体密度(1018~1019m-3)之间变化显著。因此,初步结果证实,基于金属孔阵列电极结构产生表面等离激元共振的微波反射法可以用于核心区的等离子体诊断。当然,本文的仿真模型中金属孔阵列结构忽略了实际电极结构的有限尺寸效应,并且只考虑了微波垂直入射的情况,因此这种微波诊断方法还有待进一步的试验验证。 本文对微波通过金属孔阵列结构在有/无等离子体2种情况下的传输特性进行仿真研究,通过反射频谱和归一化传输系数等分析电极结构参数和等离子体参数对微波传输特性的影响。结果表明:微波通过金属孔阵列结构会产生2种具有不同特性的表面等离激元共振模式;改变金属孔阵列结构参数时,共振频率有漂移现象;低频模式的反射随等离子体密度的增大而增大,而高频模式的反射则呈相反的响应,并且发现在等离子体密度为1017~1019m-3时品质因子比值Q/Q0随等离子体密度的增大而增大。因此,本文提出的微波反射法可用于射频大气压辉光放电核心区的等离子体诊断,对等离子体诊断技术的发展具有一定的参考价值。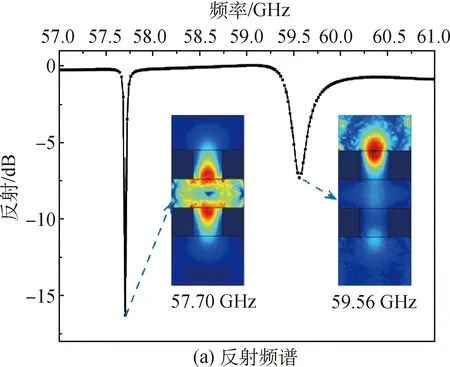

3.2 等离子体对微波传输特性的影响



4 结 语
