基于有限视觉信息的小型无人机编队控制
2021-05-10柯天成李晓丽
柯天成,李晓丽,董 鑫
(东华大学 信息科学与技术学院,上海 201620)
无人机(unmanned aerial vehicle, UAV)在摄影、军事、环境监测[1]、农业生产[2]、交通运输等方面发挥了较大的作用,并且随着无人机技术越来越成熟,其应用场景也将逐步增加。但单架无人机起到的作用是有限的,因此执行任务的时候需要无人机组的协同配合。例如,军事行动中,单靠一架无人机难以完成精准打击敌方目标的任务[3],通常都需要无人机组编队支持。生物学家通过研究生物群体行为发现,无序队形相对于有序队形来说更加费“时”、费“力”,如何更好更快地达到理想队形引起了国内外众多学者的兴趣。
编队控制问题在无人机、多智能体、机器人等领域已有多年的研究。倪利平[4]研究了智能体的角度对其线速度的影响,提出一种基于虚拟结构的分布式队形控制算法,并从理论上分析了该算法的稳定性。朱旭[5]基于行为法对无人机编队进行了控制。文献[6]将图论法和领航跟随法融合,提出一种有领航者的二阶一致性算法。文献[7]研究了具有切换和定向交互拓扑的无人机组时变编队跟踪(time-varying formation tracking, TVFT)的控制问题。这些队形控制算法为无人机编队的研究作出了很大的贡献,但均存在一些缺陷[8]:虚拟结构法很难让单个个体保持信息的同步;行为法难以用数学的方法进行稳定性分析;领航跟随法是最早提出也是目前应用最为广泛的一种编队控制方法,具有原理简单、实现过程容易等优点,但其稳健性较差,一旦前级产生误差,后级的误差将会扩大,不利于精确控制。
在实际应用中,上述算法需要依靠各类传感器、GPS全球定位系统等辅助设备来获取无人机的状态信息。但无人机的负重会影响其续航时间,因而如何降低无人机重量、延长其续航时间,同样是一个重要的课题。鱼眼镜头具有视野广、重量小等特点,经常被用于无人机的通信组网[9]。本文提出的算法以装载单目鱼眼镜头小型无人机的特征为基础,建立无人机运动学模型,仅依靠鱼眼镜头提取的视觉信息实现无人机组编队控制。虽然带有鱼眼镜头的相机视角(field of view, FOV)可以超过200°,但依然会存在视觉盲区。这使得依靠这种通信方式工作的无人机的协同能力受到严重限制[10-12],如何避开盲区并使通信畅通是本文研究的重点方向之一。
本文提出特定的代价函数用以设计避盲算法,从而使无人机之间始终保持通信。在避盲算法的基础上,引入信息一致性的分布式控制策略,以形成并保持期望的队形,最后通过数值仿真对所提出的控制方法进行验证。
1 “视觉盲区”的刻画——仿雁飞行
大雁是一种常见的候鸟,其迁徙时的独特队形引起了不同领域科学家的关注[13-14]。无人机组和大雁群之间存在很多相似之处[15-16],Li等[17]研究发现无人机飞行与大雁飞行存在共性,并利用线性系统理论给予了证明。这为本文研究无人机的控制方法提供了便利,即利用大雁飞行具有盲区的视觉特点,将具备这种视觉特点的模型应用于仅装有鱼眼镜头的小型无人机组。鱼眼镜头的广角很大[18],如同大雁的眼睛一般[17],可以看到至少-30°~210°的事物,如图1所示,β为大雁的可见视角。
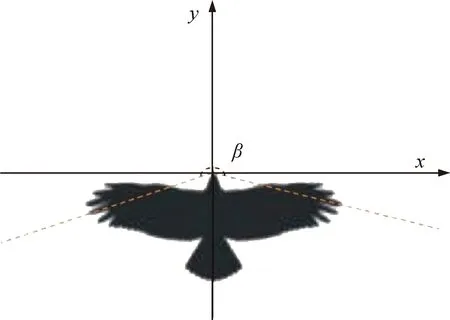
图1 大雁飞行的可见视角Fig.1 Visible view of flying geese
然而,前方的无人机可能看不到后方的无人机,即本文所述的视觉盲区,如图2所示。

图2 无人机视觉盲区模型Fig.2 The vision blind zone model of UAV

第1步:确定无人机i,其相对无人机j的角度cosγij为
cosγij=f(xi,yi,xj,yj,θj)=
(1)
式中:‖‖表示距离。
第2步:确定无人机i、j之间的距离dij,如式(2)所示。
(2)
第3步:确定无人机的最长通信距离,即鱼眼镜头的最长测距Rs[19]。

(3)
2 无人机组的数学模型
为便于描述无人机组的数学模型,采用二阶系统的无人机运动学模型[5],如式(4)所示。
(4)
式中:xi、yi分别为第i架无人机x轴和y轴方向的坐标;θi为第i架无人机前进的方向,i=[1, 2, …,n]。
这个模型的优点在于简单易懂,缺点是没有考虑实际情况下的飞行高度与飞行姿态。由于本文不需要讨论三维空间中无人机组的编队飞行,因此这个模型还是切合本文需求的。
为描述无人机的运动学问题,采用Denavit和Hartenberg提出的D -H矩阵代数方法,该方法的几何意义直观,能较好地解决动力学、计算机视觉和比例变换问题,其数学基础是齐次变换[20]。其中矩阵Ri能够反映无人机的位姿(位置和姿态),对其描述如式(5)所示。
(5)
由于本文中每架无人机通过鱼眼镜头获取的信息是相对于以己身为原点的坐标系而言的,因此需要将不同无人机的位置信息转换到世界坐标系下。以无人机i为例,其所在位置为坐标原点,飞行方向为y轴,沿y轴方向顺时针旋转90°为x轴,得到相对坐标系Fi。记F为世界坐标系,F与Fi之间转换如图3所示。在坐标系Fi(x′Oy′)下点P的坐标为(s′,t′),坐标系Fi绕点O顺时针旋转θ角度后得到F(xOy),那么点P在坐标系F(xOy)下的坐标为(s,t)。
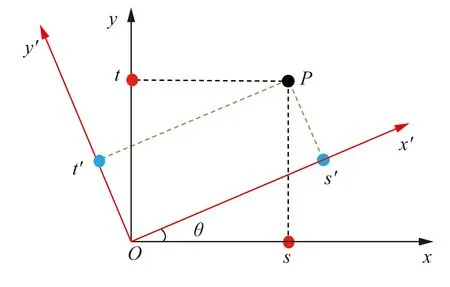
图3 坐标系旋转变换示意图Fig.3 Schematic of coordinate system rotation transformation
利用三角函数可以得到旋转后的坐标系F(xOy)中的坐标点(s,t)为
s=s′cosθ-t′sinθ
(6)
t=t′cosθ+s′sinθ
(7)
同理,可得平移坐标系后的坐标点(s,t)为
s=s′-a
(8)
t=t′-b
(9)
综上所述,经旋转、平移变化后的新坐标为

(10)
式中:P=[s,t]T,P′=[s′,t′]T。
3 存在视觉盲区的无人机组编队控制策略
3.1 约束条件
从第2节的数学模型可以看出,基于视觉信息的无人机编队虽具有一定优越性,但无法实现所有编队的控制,即部分队形会导致图像信息缺失,从而无法通过控制器对无人机组进行控制。因此,需设定一些约束条件以避免这种现象的发生。
由第2节中对“视觉盲区”的描述可以得出:
(11)

另外的约束条件为对无人机组队形的期望,即队形达到预先设定的期望并保持稳定。用相对位置描述无人机的队形,如式(12)所示。
hi-hj=Pi-Pj
(12)
对于无人机i而言,期望的队形为
(13)
对于无人机组而言,整体的相对位置为
(14)
当实际位置和期望位置使得式(14)成立时,可以认为整个无人机组的飞行编队达到期望状态,即在保持速度和飞行方向相对不变的情况下,无人机组可持续保持队形稳定。
3.2 代价函数的设计
根据“视觉盲区”的物理刻画来设计代价函数,即对“视觉盲区”这一概念进行数学描述。通过代价函数J规范边界值、编队等信息,如式(15)和(16)所示。
(15)
(16)
式中:E为位置信息函数,当无人机组达到期望相对位置时,E为0。
(17)
设定比值关系函数Vij表示实际与期望的距离信息,为消除由于符号引起的误差,其值为非负数。
(18)
本文所设计的代价函数包含角度、位置及编队信息,将多种信息融合在同一个代价函数中,不仅可以简化公式,还能使代价函数成为控制律中的一项。利用梯度下降法寻找最优解,最终使无人机达到期望状态。
在第2节对盲区的刻画中,已提及最远视距,表明每架无人机的视线是有范围的,不可能到达无穷远处,但超过Rs后代价函数可能会发生突变。为使函数平滑,引入光滑函数ρ(dij)[17],如式(19)所示。
(19)
3.3 避盲编队控制器
设计避盲编队控制器的目的是使代价函数降为最小值。当代价函数降为最小值时,无人机组将达到理想状态,如果还想要保持稳定,各架无人机的速度须保证一致。因此,设计如式(20)和(21)所示的控制器。
(20)
(21)
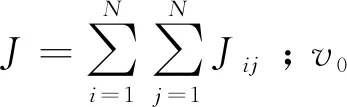
通过计算、化简可以得到Jij和Jji,如式(22)和(23)所示。
(22)
(23)
通过获取无人机局部相对状态信息,用代价函数对“视觉盲区”进行刻画,并在代价函数中加入了位置信息,结合速度一致性理论,最终提出这种可实现自主控制的编队算法。这种算法适用于装载了单目鱼眼镜头、依靠鱼眼镜头获取局部相对位置的小型无人机组的编队飞行。
4 仿真结果
在实际仿真模拟时,设定3架无人机的初始位置(需3者互在对方的盲区外),设盲区角α=30°,通信距离Rs=200 m。通过上述视觉盲区的代价函数及速度一致性算法进行数值仿真计算,设定采集时间为0.01 s。3架无人机的初始状态如表1所示。

表1 3架无人机的初始状态Table 1 Initial states of the three UAVs
同理,机组期望队形的设置也要求每架无人机互在彼此的盲区之外,期望的编队队形、航向如表2所示。

表2 3架无人机的期望状态Table 2 Expectation states of the three UAVs
基于有限视觉信息编队控制的仿真结果如图4所示,图中3条曲线分别表示3架无人机的运动轨迹。在3架无人机进行编队飞行时,每架无人机都在其他无人机的盲区外,同时通过速度一致项的作用,无人机组最终达到期望相对状态(如表2所示)。达到期望相对状态后,无人机组会根据预编队队形稳定飞行。

图4 基于有限视觉信息编队控制仿真过程图Fig.4 Process chart of formation control simulation based on limited visual information
无人机组最终状态的数值仿真结果如表3所示。

表3 3架无人机的最终状态Table 3 Final states of the three UAVs
此外,用本文的控制算法对在盲区外(α=30°)的无人机组进行数值仿真,结果表明,无人机组渐近收敛到期望的速度和航向,最终形成不同形状的编队队形,如图5所示。由于每架无人机均位于其他无人机的盲区外,在形成队形的过程中无人机之间不会发生碰撞。
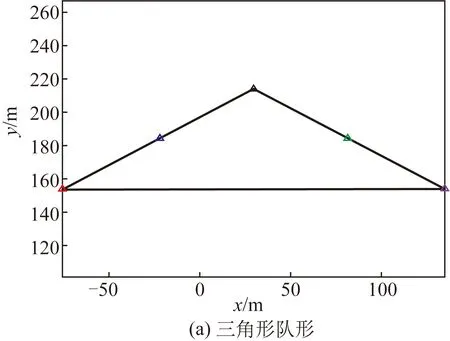
图5 不同形状的编队效果Fig.5 Formation effects in different shapes
5 结 语
为解决动态环境中的无人机组编队控制问题,本文引入代价函数来处理鱼眼镜头获取的视觉信息,并考虑视觉约束与最终位置期望,设计所对应的控制器。利用梯度下降算法将无人机组逐渐控制到稳定的预先指定的编队位置,避免无人机之间发生碰撞。仿真结果验证了本文理论研究的有效性。
