杜鹃搜索在无线传感器网络定位问题中的应用

徐行健,纪兆华,孟繁军

(1.内蒙古师范大学 计算机科学技术学院,内蒙古 呼和浩特 010022; 2.北京信息职业技术学院 计算机与通信学院,北京 100000)

0 引 言

由于近年来射频技术、嵌入式制造工艺、微电子技术的发展,无线传感器网络(wireless sensor network,WSN)的应用范围更加广阔,被广泛运用于各种探测任务,如搜索、营救、灾后重建、环境监测、目标跟踪[1-2],其中包括了大量的民用和军用项目。与传统的无线网络相比,无线传感器网络有如下不同:① 一般情况下,它比传统的无线网络包含了更多的节点;② 因为各个节点主要采取电池供电,所以它们在设计的时候,必须考虑节能的问题;③ 节点所处的环境不确定性往往很大,在一些设计用途中甚至可以说是恶劣的,这就导致定位信号可能存在一些误差。无线传感器网络的主要特点有[3]:① 规模大。有大量的节点被部署在广大的范围内,这有利于增加系统的高可用性,同时也减少了监测盲区。②自组织。无线传感器网络由其内节点自主创建,不存在或无法进行人工干预。③ 高动态。出现故障或者电池用完的节点会自动退出网络系统,同时也可以根据任务情况,实时添加新节点到网络中。

只有在精确定位了传感器位置的前提下,人们才能有效利用传感器传回的数据,而那些被定位错误的传感器传回的信息往往都是无效的。因此无线传感器网络中的一项基础研究就是传感器的定位问题。目前定位算法主要分为基于测距技术的定位算法和无需测距技术的定位。基于测距技术的定位算法主要利用了三角法或者最大似然法求得节点坐标,如AHLOS、RSSI、TOA[4],而无需测距技术的定位算法主要利用了传感器网络的连通性来求解坐标,如APIT、DV-HOP[5],其中基于测距技术的算法使用场景更为广泛[6-7]。

然而传统的无线传感器定位算法存在着较多问题,如定位精度不够高、算法运行时效率较低等缺点。为了克服这些缺点,近年来效果较好的方法是采用元启发式搜索[8-9]。元启发式算法的主要思想是:在很难获得最优解或者求最优解的算法复杂度太高的情况下,放弃求最优解,转而在短时间内去求得一个次优解[4]。如果算法设计得当、参数合理的话,那么元启发式算法可以在一个很短的时间内求得一个极为逼近最优解的次优解。

杜鹃搜索算法[10]是近来提出的一类元启发式算法,它模仿了自然界中杜鹃繁衍的过程:杜鹃会将自己的蛋放到别的鸟的蛋巢里,而且杜鹃的蛋会尽量模仿该蛋巢中其他蛋的样子;当该蛋巢的鸟回巢后,有一定概率会将蛋巢内最不像自己种类的蛋踢出蛋巢,而最像的蛋会得到优先抚育。因为杜鹃搜索算法是一种基于群体的元启发式算法(类似遗传算法或者粒子群算法)[11-12],同时也引入了一些其他类型启发式搜索算法的优点,所以杜鹃搜索算法被认为是一种极具潜力的最优解寻找算法[13]。本文基于杜鹃搜索算法,设计和实现了一套新的无线传感器定位算法,经过实验验证,其有着更加优秀的定位精度与运行时效率。

1 方 法

无线传感器网络有很多种构建模式,本文算法是基于如下一种常见的传感器网络设计的，即监测域中部署了大量的节点,但是这些节点的具体位置坐标是不可知的。因为人工定位节点是不现实的,所以利用GPS的方式来获取节点位置。由于GPS模块价格较高,并不能给所有的节点都搭载GPS定位模块,而是给网络中的一部分节点搭载。通常称这些搭载GPS的节点为锚定节点(anchor node),其他需要利用锚定节点来定位自身的节点成为目标节点(target node)。目标节点可以通过和锚定节点进行通信,来估算出自己和锚定节点间的距离,进一步通过不同的算法在监测域中进行准确定位。

在基于距离的定位算法中,传感器节点有2个参数比较重要,一个是传感器定位信号的精度,另一个是传感器信号的传播范围。这2个参数一般呈反比,精度高的传感器其信号传播范围较短,而信号传播范围较广的传感器其精度一般较低。定位信号的精度直接影响了算法定位的准确性,本文在模拟实验部分也会讨论这一点。而信号的传播范围,决定了监测域内所要投放的锚定节点的数目。一个目标节点只有成功地与3个或者3个以上的锚定节点成功通信,得到相应的距离后,才能被算法定位,因此信号范围越广,目标节点就会成功地联系到更多的锚定节点。

本文设计和实现的算法是基于SCIPY[14]编写的,SCIPY是一个Matlab的开源免费替代软件。利用伪代码算法可以求得一个目标节点的坐标。对传感器网络中所有节点利用如下算法进行逐个定位后,即得到了各个节点的估计位置,完成定位任务。基于杜鹃搜索的无线传感器定位算法如下：

输入:标节点和锚定节点的距离数组m-target。

输出:目标节点的估计坐标target-cal。

1.初始化一个n×2的矩阵nest保存n个点的二维坐标;

2.初始化一个n维数组fbest保存nest中每个点的目标函数值;

3.FOR迭代循环n-gen次

4.根据fbest里最小值出现的位置选择当前的最佳点a;

5.随机选择一个不同于点a的点b;

IF点c的目标函数值小于点b的目标函数值 THEN

6.在点a周围利用随机行走的方法生产点c;

7.用点c代替点b存储在nest中,更新fbest中对应的目标函数值;

8.END IF

9.IF生成了一个在[0,1]区间内的小于常数pa的随机数 THEN

10.根据fbest里最大值出现的位置选择当前的最坏点bad;

11.随机生成一个点代替最坏点bad,更新相应的fbest;

12.END IF

13.END FOR

14.根据fbest里最小值出现的位置选择当前的最佳点target-cal;

OUTPUT target-cal。

上述算法主要有以下3个要点。

(1) 迭代次数n-gen。迭代次数是影响算法最后能否收敛的主要因素之一。如果迭代次数过小,算法还没有收敛就已经结束,那么得到的定位值不准确;如果迭代次数过大,会让算法再收敛后继续迭代,那么使运行时间显著增加,造成不必要的浪费。迭代次数的取值必须根据经验确定,下文的模拟实验中会详细讨论。

(2)目标函数f(x,y)。目标函数的作用是评价每个估计坐标点的好坏程度,如果一个坐标能让目标函数拥有更小的值,那么这个坐标就更加接近于目标节点真实的坐标。

本文算法采用的目标函数为：

(1)

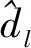
(3) 随机行走。用随机行走的方法来产生一个最佳点附近的点。随机行走方法可以选择基于正态分布的随机行走,也可以选择基于Levy飞行的随机行走。在实际的测试当中,发现对于无线传感器定位问题,采用基于正态分布的随机行走,效果更加。因此本算法采用基于正态分布的随机行走，即

Pnew=Pold+stepsizePmorm

(2)

其中:stepsize为随机行走步值;Pnew为新生成的点;Pold为起始点;Pnorm为一个从二维正态分布中随机抽取的点。

模拟实验的结果如图1所示,其中：“□”表示目标节点的实际位置；“×”表示算法定位出的目标节点位置；实心“·”表示锚定节点的位置。该次试验中用4个锚定节点去定位12个目标节点,每次定位迭代了2 000个循环(n-gen),从图1可以看出效果比较好,1个点被定位出来。对于每个目标节点,算法从(0,0)开始逼近目标节点的真实坐标,最后收敛于目标节点,中间迭代过程中产生的估计点也被绘制在图中,产生了一条点迹线,据此可以直观地看到算法是如何收敛的。

图1 本文算法对目标点的逼近

2 验 证

本文的仿真模拟实验基于SCIPY开发,所有实验都是在同一台计算机(CPU是Intel Xeon E3 1230v2, 4核心8线程, 3.4 GHz主频, 16 G内存)上进行的。模拟了一个边长为R=140(具体的距离量纲在实验中无关紧要)的正方形监测域,其中每个节点的信号传播半径是r=10,也就是说,如果目标节点和锚定节点的直线距离在r以内的情况下,目标节点可以联系到锚定节点,从而被测距。R为r的1.4倍,这是一个实践中得出的比较好的经验公式[15-16]。每次试验总共有目标节点数n-targets=100,锚定节点是目标节点的10%,即n-anchors=10,这个百分比也是实践中经常采用的一个数值。如果锚定节点过少,会造成大量的目标节点联系不到3个或3个以上的锚定节点,造成无法定位。

当n-gen=2 000时,本算法的仿真实验结果如图2所示,从图2可以看出大多数目标节点都被准确定位。仿真实验表明,当R为1.4r时,投放目标节点数10%的锚定节点就可以很好地定位出绝大部分目标节点,定位率(可定位目标节点数和总目标节点数的比值)达到了99.14%。

图2 模拟实验的结果

2.1 定位结果的评价

本文主要使用好点率(good points ratio,GPR)来评价定位结果的精度，计算公式为:

GPR=Ngood/Nl

(3)

其中:Nl为该次模拟实验中总共被定位出的点(也就是处于3个或3个以上锚定节点信号范围以内的点)的总数;Ngood为好点的总数。若某点算法定位出的坐标和该点真实坐标间的欧几里得距离小于节点信号范围0.001[3],则称算法定位出了一个好点(GP)。根据无线传感器的通讯原理,随着传感器信号范围的变大,其本身的定位信号被干扰的程度就会越大。若好点率过小,则说明大多数无线传感器都没有被精确地定位到,因此好点率直接反应了算法定位的好坏。

2.2 鸟巢中蛋的数目n对算法的影响

通过算法的分析可以知道,巢中蛋的数目n只要不是很少,对算法定位效率的影响不明显,这和粒子群算法中得出的结论一致。保持算法的其他参数不变,只改变参数n的大小,得到的实验结果见表1所列。当n=20时,好点率就已经稳定在97%左右。因此下文中其他的模拟实验统一选择n=20。

表1 蛋的数目n对算法的影响(基于10次实验)

2.3 迭代次数n-gen对算法的影响

迭代次数n-gen是影响算法定位效果的主要因素之一。箱线图如图3所示，从图3可以看出，n-gen在2 000和3 000的时候好点率的均值和方差都取得了较优的结果,绝大多数的点都得到了精确定位。迭代次数过少会使算法过早收敛,迭代次数过多则浪费时间。通过算法的时间复杂度分析可知,算法的时间复杂度是O(Nn-gen),N为目标节点的个数。下文的模拟实验中,使用的迭代次数统一为2 000。

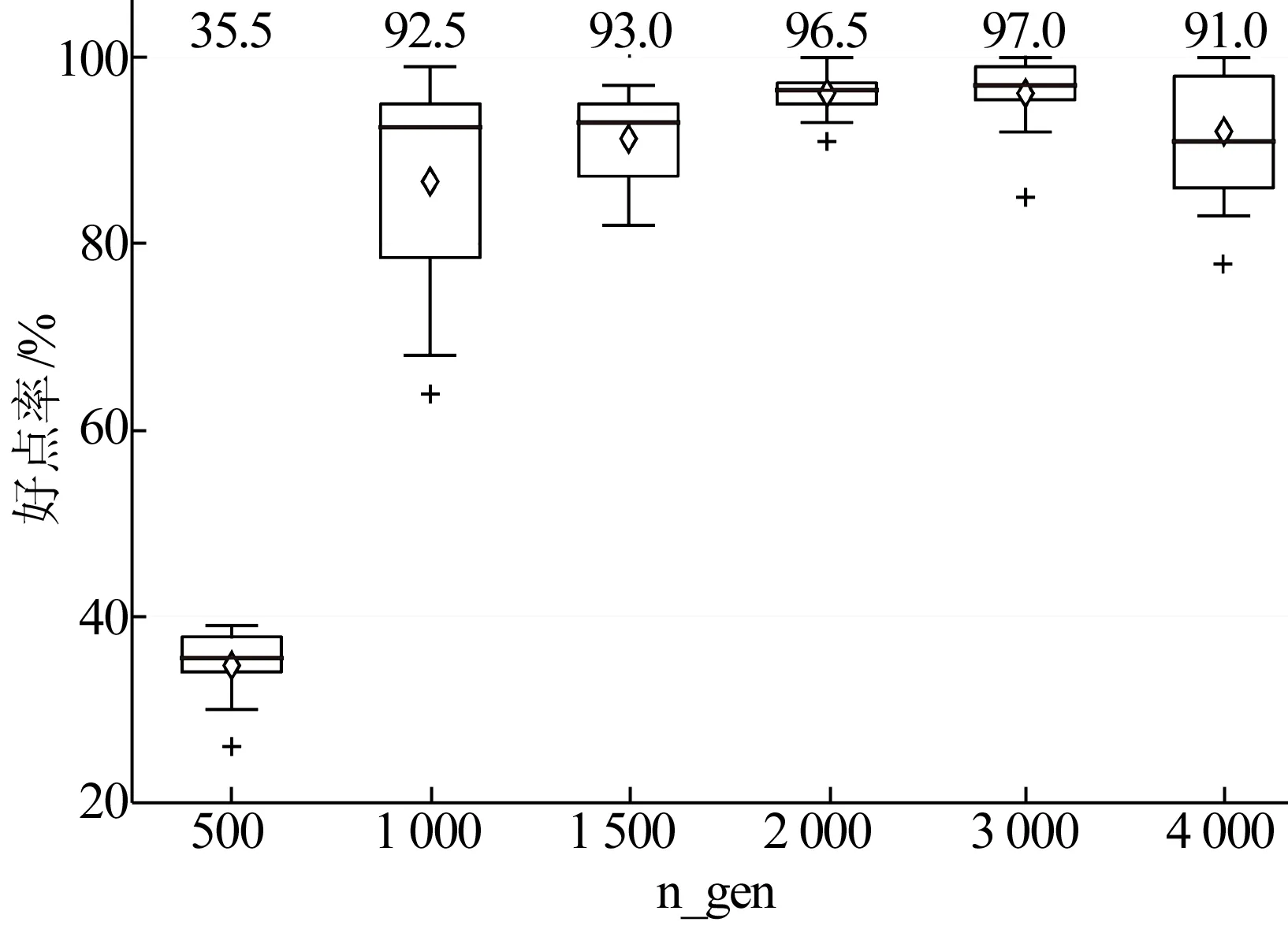
图3 n-gen对算法好点率的影响

2.4 随机行走步值stepsize对算法的影响

随机行走步值也会影响算法定位。如果步值过小,那么在有限的迭代循环里,收敛过慢；如果过大,那么有更大的概率错过最优解,算法的收敛也很慢。步值stepsize对算法好点率的影响如图4所示，从图4可以看出,在迭代次数为2 000的时候,步值为0.5的效果比较好。

图4 步值stepsize对算法好点率的影响

2.5 干扰值noise对算法的影响

在上面的实验中,均没有模拟测距信号被干扰时的情况(即干扰值为0)。本组模拟实验中,按照(4)式产生了定量的干扰，即

(4)

其中:d为目标节点和锚定节点间的欧几里得距离;noise为干扰值；randnorm为一个服从标准正态分布中随机采样得到的随机值。通过(4)式,可以产生了一个被干扰后的距离。干扰值noise对算法好点率的影响见表2所示，从表2可以看出,当干扰过高时,好点率显著降低。

表2 干扰值noise对算法好点率的影响(基于10次实验)

2.6 本文方法和其他方法的比较测试

各个方法的好点率和运行时间的比较如图5所示。

(a) 好点率

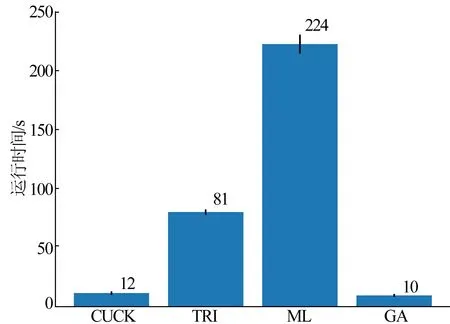
(b) 运行时间图5 各个方法好点率和运行时间的比较

本文的方法(CUCK迭代次数为2 000,步值为0.5)和以往的几个具有代表性的方法进行比较。选取用来对比的方法有三角测量法(TRI)[6]、最大似然法(ML)[6]、基于遗传算法的定位方法(GA)[9]。三角测量法和最大似然法在相应的参考文献中均有可以直接使用的程序用来测试,而基于遗传算法的定位方法,并没有直接可用的测试程序,因此根据参考文献中的伪代码实现一个测试程序。为了使各个算法的差异表现得更加显著,本次实验对在边长为1 400的正方形检测域分布的1 000个节点(其中有100个已知坐标的锚定节点)进行了定位,每个方法重复进行20次,模拟测试数据的干扰值设置为0.001。本次测试主要对各个方法的好点率以及所需时间进行了比较。

从图5可以看出,本文的方法在定位精度(好点率)方面和经典的基于距离的定位方法较为相似,而在运行时间上,大幅度领先三角测距法和最大似然法。和遗传算法相比,运行时间虽然略差,但是定位精度却有所提高。这充分体现了元启发式搜索在短时间内寻找次优解的强大优势。传统的最大似然法虽然定位精度非常高,但是求解过程需要进行大量的迭代优化计算,所需运行时间太长,导致这种方法在实时性要求比较严格的环境下应用受到很大限制,而本方法只需极短的时间就可以得出一个和最大似然法相差不大的定位结果。

3 结 语

本文基于杜鹃搜索,设计和实现了一套新型无线传感器定位算法；该算法具有定位准确、结果稳定和运行时效率高等特点。通过一系列的模拟仿真实验,相比于其他基于测距的无线传感器定位算法,本文提出的算法在无线传感器网络定位问题中有着更加良好的表现。在实验验证的基础上,给出了算法中各个主要参数的最佳参考值,可以提供给其他科研或者工程人员使用。本算法的并行化程度很高,在接下来的工作中,可以对该算法并行化,达到一个更加优秀的并行加速比[17],从而进一步提高算法的效率。可以考虑采用GPU编程[18]或者诸如Hadoop[19]这种分布式计算的方式,应用到超大传感器网络中,实现节点的快速高精度定位。