基于GMSD的新混合损失函数
2021-05-10檀结庆朱星辰蔡蒙琪
檀结庆,朱星辰,蔡蒙琪
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
近十年来,神经网络在各个领域取得了巨大的成功。神经网络的思想诞生于20世纪80年代,在2012年的ImageNet比赛上,文献[1]使用神经网络方法取得成绩后,神经网络领域迅速再次成为研究者们关注的焦点。经过几年的发展,从图像处理、语音识别到几何造型,神经网络算法的应用推动这些领域的研究取得了巨大的进步。
在图像处理上,卷积神经网络(convolutional neural network,CNN)也成为研究者关注的主要方法。图像超分辨重建,即将低分辨率图像(low resolution,LR)恢复成高分辨率图像(high resolution,HR),也在使用CNN方法后得到了飞速的发展。
卷积神经网络方法的应用让单幅图像超分辨率(single image super resolution,SISR)问题得到了较好的解决。文献[2]提出了SRCNN模型,第1次将CNN方法应用到图像超分辨率(super resolution,SR)问题上。SRCNN是一个端到端学习LR图像到HR图像映射的高效网络,它不需要进行人为的特征处理,并取得了令人满意的表现。之后,大部分研究都专注于提出更高效的网络结构来学习LR图像到HR图像之间的映射。一系列基于CNN的模型被提出[3-13],从上采样方法,到中间层的特征提取方法与特征处理方法,再到映射结构,研究者们在CNN模型的结构方面做了很多工作,并取得了令人瞩目的进步。然而,大多数模型只是针对其他研究领域中模型结构的变化,对超分辨率领域的CNN模型结构进行了改动,大体上倾向于组建一个更深更复杂的网络结构。这意味着在模型训练上需要更多的资源、时间与技巧,使得CNN模型在网络结构方向上的改进逐渐陷入瓶颈。
在网络结构改进逐渐陷入瓶颈的同时,作为CNN模型中的重要一环,损失函数层的改进却一直没有受到很大的关注。CNN模型中,l2损失函数是最早被广泛使用的损失函数。鉴于它的可微性与实现上的简单性,l2损失函数被使用了相当长的时间。文献[14]通过对比实验的方法验证了l1损失函数具有比l2损失函数更快的收敛速度且不亚于l2损失函数的准确性。因而l1损失函数在SR领域逐渐代替l2损失函数成为最广泛使用的默认损失函数。但在此之后,再没有一个得到广泛应用的新的损失函数。一方面,这是因为超分辨方向的研究者们对该领域关注度不够,另一方面,这也与图像处理中图像质量评估(image quality assessment,IQA)选择的主观性及其能否与深度学习的损失函数层相结合有关。
针对网络改进趋于停滞和损失函数没有受到关注这一问题,本文聚焦损失函数层并强调IQA领域在图像处理中对神经网络的重要性,提出一种新的损失函数,通过实验验证,使用适当的损失函数可以让神经网络模型在不改变原有结构的基础上提升模型效果。
1 相关研究
本文的目标是对卷积神经网络的损失函数层进行改进,因此只讨论基于CNN的图像超分辨方法。因为损失函数层的构造与图像质量评估方法息息相关,所以需简要介绍图像超分辨方法及图像质量评估方法的相关情况。
1.1 SISR
SISR问题的发展可以大致分为3个阶段。第1阶段的插值方法通常基于采样理论,如最近邻插值、线性双三次插值。这些方法速度很快,但是在细节重建上的表现一般。第2阶段方法的主要思想是建立LR图像与HR图像之间的映射关系,比如邻域嵌入方法和稀疏编码方法。它们通常优于插值方法,但需要大量存储空间对字典进行存储,同时运行速度较慢。
在第3阶段,研究者们大都专注于构建一个端到端的CNN网络模型,使用庞大的训练数据库来学习低分辨率图像到高分辨率图像的映射。文献[2]提出SRCNN,并将CNN模型第1次运用到超分辨率问题后,SISR领域迅速出现很多CNN模型。早期模型通常使用经过预处理的LR图像作为输入,即通过上采样将LR图像放大到HR图像尺寸,再将其输入网络。这种方法增加了计算复杂度,且上采样通常使用插值方法,会产生人眼可见的缺陷。为了解决这个问题,文献[3]和文献[4]对上采样方法进行了改进,让神经网络直接使用LR图像作为输入,加快了CNN网络训练与应用时的速度。与此同时,包括DRCN[5]、LapSRN[6]、SRResNet[7]和EDSR[8]等在内的众多CNN模型被提出。其中,EDSR模型首次引入残差结构以及DRRN[9]模型引入稠密网络结构,可视为此阶段的重要进展。然而,后续更多的模型改进通常是基于上述两者模型结构的重组与解构,缺少重大创新。
1.2 IQA
SISR问题中使用的CNN模型大致可以分为3个部分:特征提取与特征处理的中间部分、SISR问题特有的上采样部分以及损失函数部分。其中,损失函数是CNN模型中最为重要与基础的一环,针对不同问题选择合适的损失函数不仅能够提升收敛速度,还能提升训练效果,提高模型性能。在SISR问题中损失函数的选择需要考虑IQA的选择与构造的损失函数的可微性。
在图像超分辨领域,峰值信噪比(peak signal noise ratio,PSNR)与结构相似性(structural similarity index measure,SSIM)是广泛使用并得到认可的2种图像质量评价指标,它们都是基于参考图像的评价方法。从这2个评价标准出发,研究者们对不同的损失函数进行了研究与尝试,期望模型可以在这2个指标上得到突破。
PSNR是一种基于2幅图像像素点进行比较的指标。从PSNR公式出发,通过均方误差(mean square error,MSE)的表达式,可以得到l2损失函数,而l2损失函数的可微性与凸性等特点,让它在优化问题中得到了广泛应用。文献[13]通过实验验证了使用l1损失函数能够加速模型收敛,同时最终收敛时得到的模型精度不会有太大差别。由此,l1损失函数逐渐代替l2损失函数成为图像超分辨领域中模型训练的默认损失函数。尽管PSNR在客观上能够解释2张图像的相似性,但PSNR是基于像素点进行的比较,因此在PSNR值较高时,也可能出现人眼视觉不佳的图像。为了解决这个问题,IQA领域的研究者们提出了另一个基于图像统计信息的指标,即SSIM。
SSIM指标是基于2幅图像的均值、标准差等数据进行比较的方法,相比于PSNR,更注重整体图像在人眼视觉中的感受。文献[13]从SSIM指标出发,分别分析了SSIM和基于SSIM改进的多尺度结构相似性(multi-scale structural similarity index measure, MS-SSIM)评价指标,并提出了l1与MS-SSIM混合的新的损失函数。这种新的混合损失函数相比于单一地使用l1或者MS-SSIM指标,会让模型表现有所提升。
除了以上2种指标,IQA领域还在不断提出新的指标,以期达到能够符合人眼视觉评价的效果。比如基于MS-SSIM,根据局部信息加入权重策略进行改进的基于信息权重的结构相似性指标(information content weighted structural similarity measure,IW-SSIM)。方差扩大因子(variance inflation factor,VIF)指标则根据扭曲图像与真实图像之间共享信息进行判别。特征相似性(feature similarity,FSIM)则从视觉感知中重要的相位一致性出发,利用2幅图像的局部相位一致性与梯度对图像质量进行度量。
2 图像超分辨的损失函数层
本节首先从SSIM出发,对SSIM和MS-SSIM损失函数进行阐述,然后提出基于梯度幅值相似偏差(gradient magnitude similarity deviation,GMSD)的损失函数,并提出基于l1、MS-SSIM和GMSD的新的混合损失函数。
2.1 SSIM与MS-SSIM
常用的l1损失函数和l2损失函数都是基于PSNR指标提出的损失函数。由于PSNR是基于像素点进行比较的指标函数,常会忽略人类视觉的感受。SSIM指标与PSNR不同,是一种从人眼视觉出发,基于图像的统计信息进行比较的指标函数。
令
有
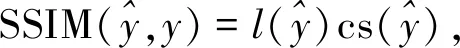
(1)
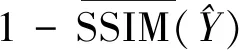
(2)
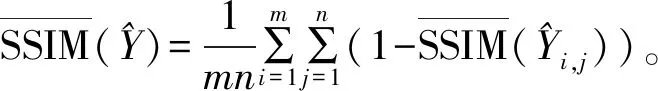
从(2)式可以看出,SSIM损失函数的计算与选取的邻域大小相关。由于要使用邻域像素点,在边界时需要通过填充,以解决边界点的计算问题。对此求偏导数:
其中
2GσG((i,j)∈(k,l))×
(3)
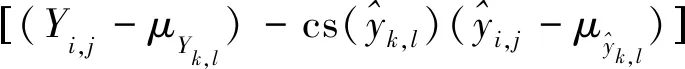
(4)
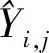
其中:lq、csq表示在缩小2q倍后的图像上求得的值;M为设定的最大缩小倍数;α、βj为可设定的参数。本文设定为α=1,βj=1(j=1,…,M)。由此,MS-SSIM损失函数写作:
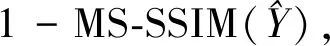

MS-SSIM的反向传播导数可以写作:
2.2 GMSD
文献[14]提出了基于参考的图像质量评价方法GMSD。GMSD在IQA领域的表现优于SSIM与MSK-SSIM。与SSIM相同,GMSD也是一种基于统计信息的图像质量评价方法。GMSD从图像的梯度信息出发,提取结构信息。自然图像往往具有类型丰富的局部结构,而不同的结构在失真时会有不同的梯度变化。鉴于局部质量退化引起的图像全局变化可以反映图像质量,GMSD方法先通过计算局部梯度相似性来衡量局部图像质量,再通过计算局部图像质量的标准差来衡量图像全局的质量。GMSD的公式如下:
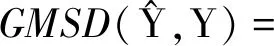
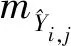
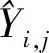
对上述3个部分分别求偏导:
其中,H1((i,j)∈(k,l))与H2((i,j)∈(k,l))分别表示点(i,j)在图像块(k,l)中相应的h1与h2卷积核系数。一方面,GMSD在IQA领域拥有优于SSIM、MS-SSIM的良好表现,更符合人类视觉;另一方面,GMSD中的梯度计算与神经网络有着天然联系,使它可以自然地应用于反向传播过程中。
2.3 基于GMSD的混合损失函数
从上述说明可以看出,单纯使用l1损失函数并不能使训练出的模型在视觉上达到最佳效果,而使用MS-SSIM训练出的模型则容易在平滑区域产生一致性偏差,因此,本文提出使用l1损失函数、MS-SSIM损失函数及GMSD损失函数相结合的新的损失函数,其表达式为:
Lmix=αLl1+βLGMSD+
(1-α-β)LMS-SSIM。
一方面,该损失函数使用l1这种像素级损失函数,保证了收敛速度以及模型的准确性;另一方面,使用LMS-SSIM损失函数对图像整体相似性进行了调整。最后,加入的LGMSD损失函数又发挥了GMSD指标在IQA领域优于MS-SSIM评价指标的特性,让产生的图像更符合人类视觉,也利用了求取图像梯度与卷积操作的天然联系,融入了神经网络的训练过程。经过实验验证,参数设置为α=0.8、β=0.1、d2=10时,模型训练可以达到良好效果,且该函数比单纯使用l1损失函数具有更快的收敛速度以及更好的收敛性。具体实验过程与结论将在第3部分阐述。
3 实验结果
本节将给出改进的损失函数在不同测试集上的效果。首先介绍实验使用的数据集与模型以及实现细节;然后给出实验结果并与其他方法进行对比。
3.1 实验数据集
实验使用广泛采用的DIV2K数据集进行训练,并在Set5、Set14、BSDS100、Urban100和Manga109数据集上进行测试。这些测试数据图片涵盖范围广泛,能够有效验证模型的泛化性能。所有的实验都在RGB空间完成,并使用x2,x3,x4的上采样倍数进行训练和测试。
3.2 多尺度残差模型
本文使用多尺度残差网络(multi-scale residual network,MSRN)模型[12]作为实验模型。MSRN模型首先使用3×3的卷积核从低分辨率图像中提取特征,然后使用8个多尺度残差块(multi-scale residual block,MSRB)进一步处理,并将每一步的结果进行串联,接着用1×1卷积核作为瓶颈层进行特征组合筛选,最后使用亚像素卷积完成上采样。MSRB的具体结构如图1所示。
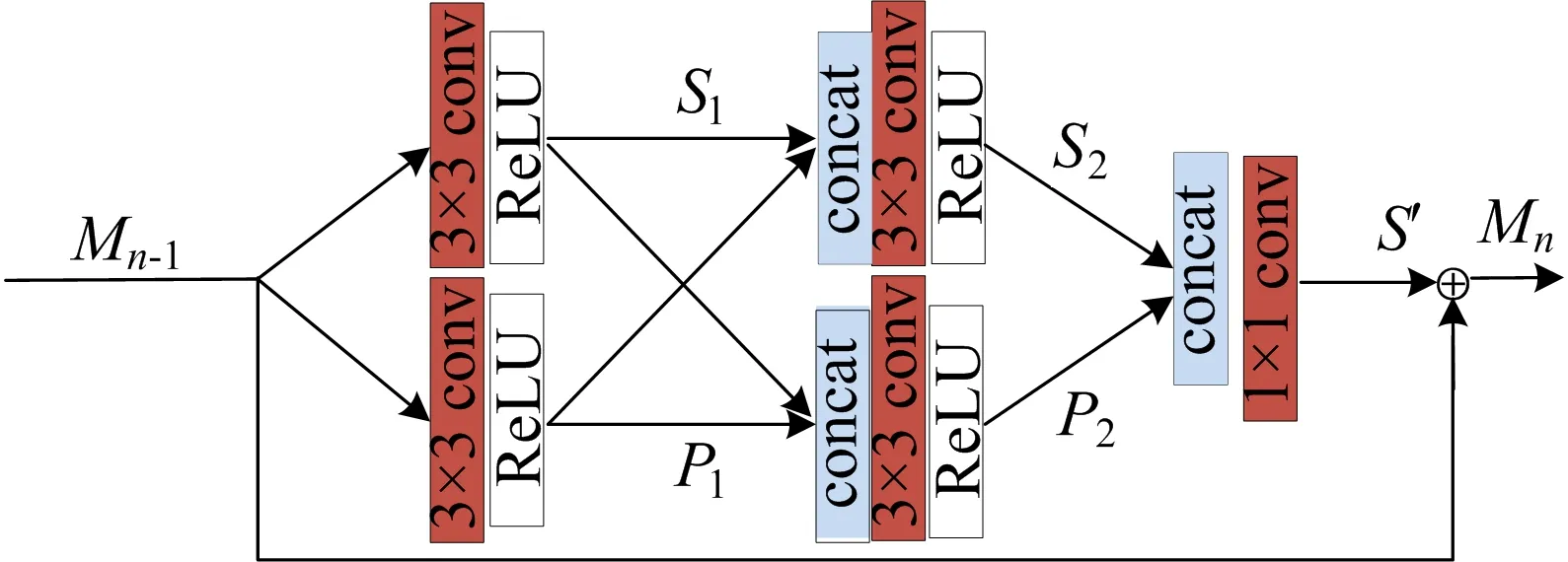
图1 MSRB结构
3.3 实验结果与结论
在实验中使用了MSRN中的模型参数,将模型使用的l1损失函数更换为本文提出的基于GMSD的混合损失函数,并将实验结果与原始的MSRN模型进行对比。考虑到图像质量评判标准的适用性,沿用PSNR/SSIM 2个广泛使用的图像评价指标。实验结果见表1所列。
实验均在MSRN模型基础上进行,第1列是使用l1损失函数进行训练的结果,第2列是使用文献[13]提出的损失函数进行训练的模型结果,第3列为使用本文提出的损失函数进行训练的结果。通过表1的实验对比,可以发现,采用本文提出的基于GMSD的混合损失函数训练模型能够在不改动模型其余部分的情况下有效提升模型质量。
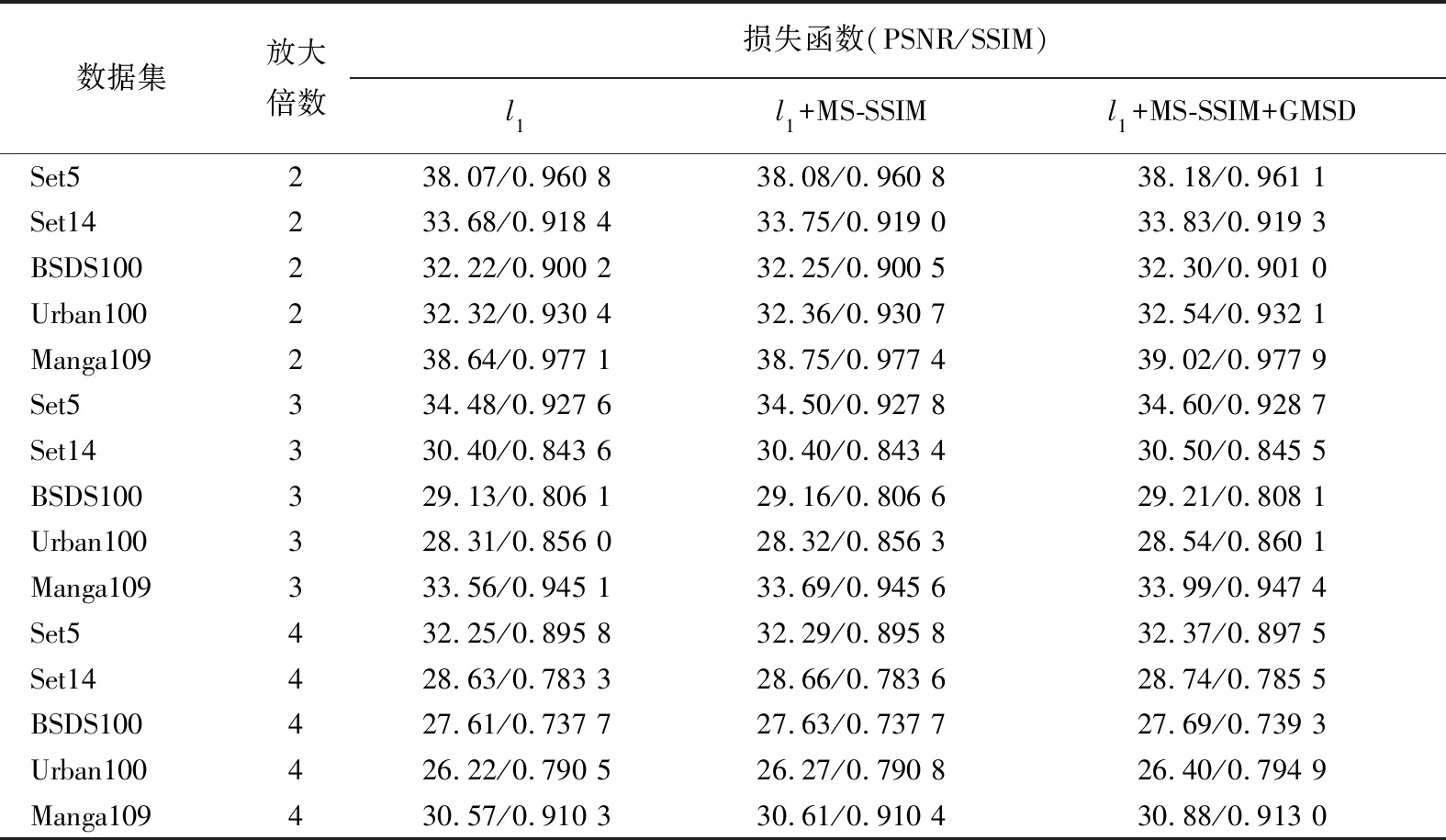
表1 PSNR数值结果
SR视觉效果如图2、图3所示。

图2 SR视觉效果一

图3 SR视觉效果二
4 结 论
本文研究了图像超分辨领域CNN模型的损失函数,提出了新的基于GMSD的混合损失函数,并通过实验,验证了在保持模型结构与参数不变的情况下,使用新的损失函数进行模型训练仍然可以大幅度提升模型性能。进一步的研究工作可以探索改进损失函数的其他方法以避免CNN模型结构的改进瓶颈。
