基于神经网络的液压混合动力车辆蓄能器SOC状态预测研究

周 鹏，吴相稷

(1.昆明冶金高等专科学校电气与机械学院，云南 昆明 650033；2.昆明理工大学交通工程学院，云南 昆明 650500)

0 引 言

液压混合动力汽车是将传统内燃机和蓄能器[1-2](Accumulator，ACC)，通过串联或并联的方式，耦合在一起驱动新型混合动力汽车。其中动力源蓄能器的荷压状态(State of Charge，SOC)是用于显示蓄能器ACC剩余压力的指标参数。该参数在车辆运行时，无法直接用仪表采集到，目前多是通过对相应物理参数的测算，并建立相关数学模型估算得出。蓄能器作为辅助动力源，其运行工作受限于诸多不稳定因素(如环境温度、振动等)影响，呈现非线性复杂特征。故能够精确且快速地预估出蓄能器的荷压参数，考量液压混合动力汽车的动力性和燃油经济性，实现对发动机和蓄能器的最优能量分配，有着重要的现实意义。

本文将通过选定的某重型串联液压混合动力车辆的参数，采用神经网络控制，对辅助动力源蓄能器的荷压状态(SOC)进行精确估计，通过对充放压的数据进行多次训练和模拟实验，应用Matlab/Simulink进行验证试验，确保所设计算法控制可靠、有效。

1 神经网络控制

神经网络算法有着较好的非线性适应能力[3-4]，通过对数据的并行处理，实现对控制对象的鲁棒稳定性和兼容性，其非线性特点可以对多参数、多变量进行计算，不再需要对被控对象的准确数学模型；通过对输入变量控制，及时输出结果，实现其较强的容错性和解决问题能力。

BP神经网络，作为一种无反馈、层内(输入层、隐含层、输出层)未互联结构，也有的是采用多层次设计结构，通过对误差的反向控制，进行神经网络训练。典型的一个隐含层BP神经网络结构如图1所示。

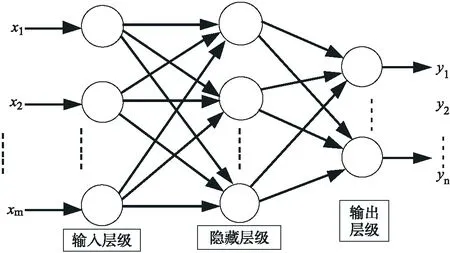
图1 一个隐含层BP神经网络典型拓扑结构Fig.1 A typical topology of BP nrural network with hidden layer

图1中，输入变量x1、x2、…、xm是控制算法模型的输入层；输出变量y1、y2、…、yn是控制算法模型的输出层。

依据神经网络算法，输入、输出对应关系如下：

(1)

(2)

(3)

(4)

式(1)～(4)中，ωij，ωjk为连接各神经元权值调节各个输入量的占重比；θk表示该神经元的阈值；η为该神经网络的设定学习速率；误差、修正系数由梯度下降法训练计算得出；ΔE是误差，tk是期望输出。

2 SOC状态神经网络预测模型

2.1 输入层

神经网络控制[3，5-6]，由多个神经元相互关联，这些简单的神经元内部连接，形成网络控制系统。本文选取节气门踏板开度、车速、车速变化率(加速度)、模式选择开关共4个参数作为输入层级的变量。神经元m=4。

2.2 隐藏层

神经网络控制的隐藏层神经元数目，一般依据下述算法经验公式得出。常见经验公式有3个，它们之间没有本质区别，所得神经元个数一般无实质性差别。

(5)

l=log2m

(6)

(7)

式(5)～(7)中，α可取1～10之间的自然数。

2.3 输出层

本文中，输出参数为液压蓄能器的荷压状态(SOC)，可知在输出层中的神经元数目为荷压状态SOC 1个。其神经网络控制模型如图2所示。

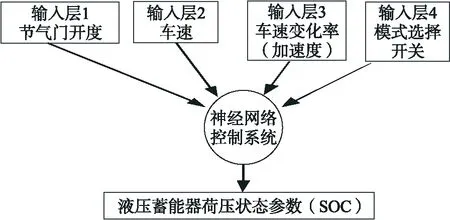
图2 液压混合动力汽车神经网络控制 液压蓄能器荷压状态SOC控制结构 Fig.2 Neural network control of hydraulic hybird electric vehicle SOC control structure for load state of hydraulic accumulator

3 仿真模型和训练数据

3.1 车辆运动的数学模型

建立车辆动力学模型，研究汽车在路面上行驶时，存在克服的行驶阻力(Ft)，有滚动阻力(Ff)、空气阻力(Fw)、坡度阻力(Fi)和加速阻力(Fj)

由车辆驱动力—行驶阻力平衡方程可知

Ft=Ff+Fw+Fi+Fj

(8)

Ff=mgfcosθ

(9)

(10)

Fi=mgsinθ

(11)

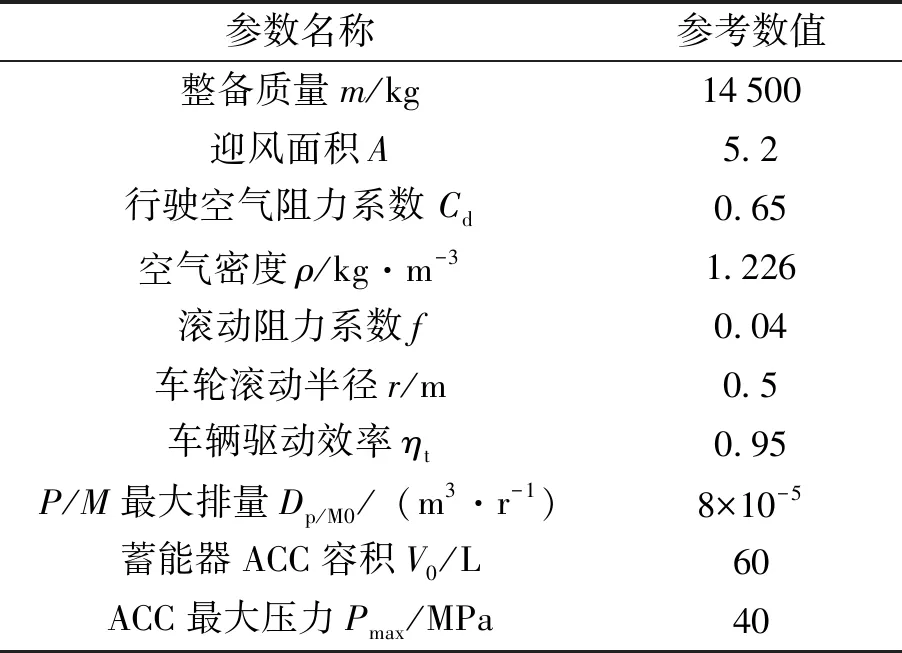
表1 所选液压混合动力汽车主要参数

式(8)～(11)中，相应参数涵义在表1仿真参数中给出。

3.2 仿真参数

本文中，选择某重型汽车改装的液压混合动力车辆为研究对象，该车的基本参数见表1。

所选液压混合动力汽车主要参数为验证液压蓄能器荷压状态(SOC)的最佳充放压参数，每次仿真时，均将蓄能器充压至满格100%。如此，可使得在加速、急加速、上坡、大负荷等工况，优先由蓄能器提供车辆行驶所需能量，降至蓄能器最低充压数值时，再由发动机提供车辆所需能量。

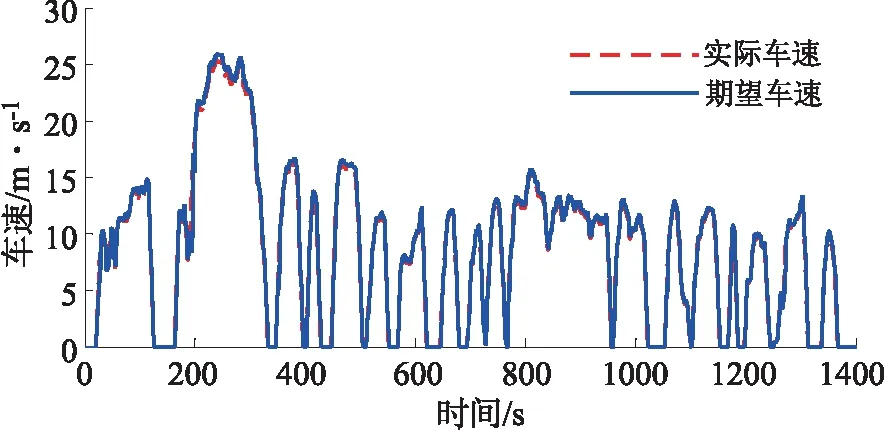
图3 实际仿真车速与期望车速高度切合 (在荷压状态开启值为0.2，关闭值为0.5时)Fig.3 The actual simulated speed is consistent with the expected speed(In the state of load, the opening value is 0.2 and the closing value is 0.5)

4 仿真验证分析

本文选用国际通用的城市工况FUDS作为仿真循环工况，来验证所设计神经网络控制策略的适应性，在仿真软件Matlab/Simulink中搭建模型，通过一系列参数的输入、处理，最后得到相应的处理结果。

经过多次训练，得出液压蓄能器ACC的荷压状态开启值为SOCstart=0.2，荷压状态关闭值SOCstop=0.5，此时发动机与蓄能器的工作协调最好，相应的参数指标如图3所示。

图4是期望车速和实际车速的关系及相应车速误差值。从图4可以看出，此车速误差值为[-1,1]，实际车速能够完全跟踪期望车速，说明所设计选取的蓄能器SOCstart=0.2，SOCstop=0.5，能够满足实际需求。

图5、6所显示的是FUDS整个仿真中，蓄能器SOC的适应循环工况变化和车辆的工作模式的变化。图7中车辆运行至200 s左右时，蓄能器SOC和工作模式迅速切换，是由于循环中在该时段内车速变化较急，蓄能器SOC在开启值SOCstart和关闭值SOCstop之间跳跃，在极少数的时间内SOC超出了这个范围，是车辆在此时急加速所致。

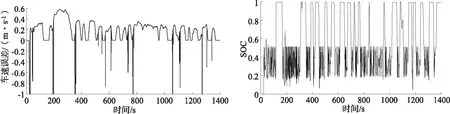
图4 期望车速与实际车速误差值 图5 蓄能器SOC适应循环工况FUDS的曲线 Fig.4 The error between the expected speed and the actual speed Fig.5 Curve of accumulator SOC adapting to cycle FUDS

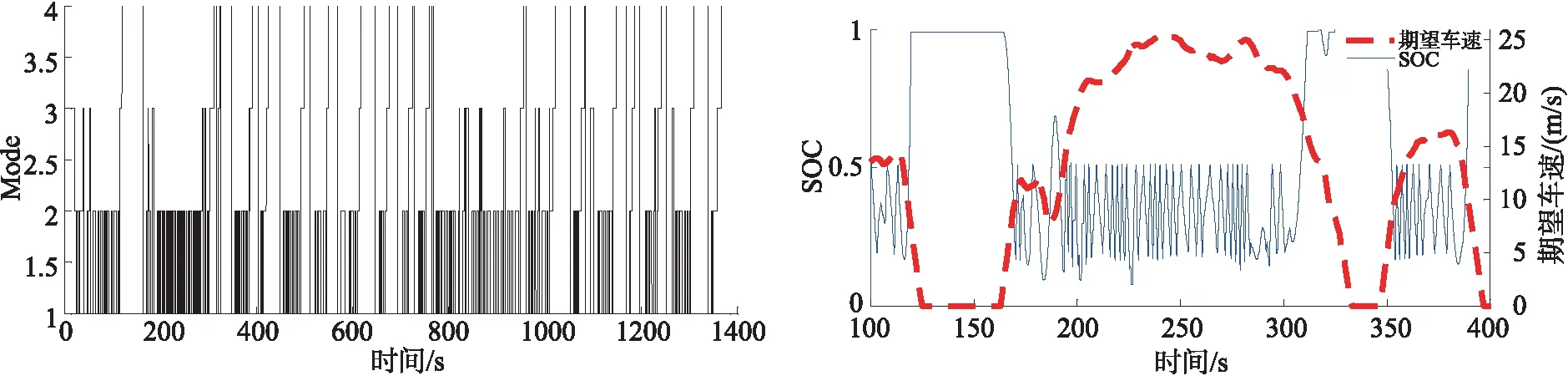
图6 FUDS循环工况下，蓄能器SOC、发动机和车辆工作模式的选择 图7 FUDS仿真工况100～400 s时，蓄能器SOC与期望车速适应Fig.6 Selection of working modes of accumulator engine and vehicle under FUDS cycle Fig.7 When the simulation condition of SOC, FUDS is 100～400 s,the accumulator SOC adapts to the expected speed

5 结 论

本工作根据液压混合动力车辆中辅助动力源液压蓄能器ACC的荷压状态参数(SOC)，较难在实际中获取，建立基于神经网络控制的液压蓄能器关键参数预估模型。选择某重型串联液压混合动力车辆为研究对象，通过对数据的多次模拟验证，得出液压蓄能器ACC的荷压状态开启值为SOCstart=0.2，荷压状态关闭值SOCstop=0.5时，发动机与蓄能器的工作协调最好。对比分析验证表明：车辆实际车速可以跟上期望车速需求，误差为[-1,1]；蓄能器工作曲线和工作模式可以适应FUDS仿真循环的要求；急加速等特需工况，SOC值的响应较好，达到了预期效果，具有一定的理论推广意义。