柱-环梁法对料仓框架结构地震响应研究
2021-05-10刘占宇
于 洋,刘占宇,梁 豪
(东北石油大学 土木建筑工程学院,黑龙江 大庆 163318)
料仓作为一种常见的存贮工业建筑,广泛应用在我国石油化工、粮食存贮行业。而在料仓实际设计过程中,由于缺少相应的行业标准与规范为依据,不同设计人员对规范的使用和理解存在很大的差异,主要反映在配筋相差较大,约有20%~30%,造成很大的浪费,也增加了施工难度。国内外研究人员从工程实际出发,进行料仓优化设计方面的研究,并取得了丰富的成果,提供许多可供研究的案例,国内外规范对料仓-框架结构的设计方法也作了许多规定[1-13],但是目前还没有一个广为接受的设计方法。理论方面国内外学者也进行了许多研究,1895年,德国学者Janssen[14]提出著名的Janssen物料压力公式,该公式简便易操作,与实际受力较为吻合,时至今日还被许多国家所采用,并被应用到筒仓设计规范中,是筒仓方向研究的基石。近些年来,有学者研究由波纹壁和立柱组成的圆柱形钢筒仓在整体荷载作用下的整体稳定性及优化设计。利用单位柱抗弯刚度变化引起的屈曲荷载系数的影响线,对每个设计阶段筒仓柱截面的变化进行了计算[15],用理想筒仓三维壳体模型的线性屈曲有限元分析结果和几何非线性有限元分析ABAQUS进行了验证,根据计算结果提出一种合理的筒仓设计方法。国内较为有代表性的研究也有很多,有分析内部散装物料的相关实验研究、筒仓结构的相关实验研究[16-17]。还有利用有限元软件ABAQUS将框架与料仓相结合的综合分析,得出更为深入的研究结论[18]。
本文在已有研究的基础上,结合工程实例,选择适合的结构方案,合理简化计算模型,在满足构造要求的基础上合理配置钢筋,不仅减小施工过程中的造价,更能提高结构的安全性。同时,为制定相关的行业设计规范提供一定的理论依据。
1 柱-环梁法料仓刚度等效理论
料仓体积庞大,而且高度较大,固定在结构上后实际上已融为一体,因此结构分析时应采用一体的结构计算模型,故料仓结构在分析过程中,为了模拟工程实际情况,将料仓简化为由八根方柱和几层环梁组成的一体柱环梁-框架结构[18],详见图1所示。

图1 柱环梁模拟图Fig.1 Column ring beam simulation diagram
根据平面刚度等效原则:
得出
其中:d2—料仓外径,d1—料仓内径,Es—铝合金弹性模量,Ec—混凝土弹性模量,b—方形柱边长,D1—相邻柱中心水平间距,D2—间隔柱中心水平间距。
拟结合某石化公司脱气及储存料仓-框架结构项目,已知料仓外径为7 216 mm,内径为7 184 mm,铝合金的弹性模量为7.0×104N/mm2,钢筋混凝土的弹性模量为3.25×104N/mm2,相邻柱中心水平间距为2 546 mm,间隔柱中心水平间距为3 600 mm,不计柱本身惯性矩。
计算建模b取值为312 mm,建模取400 mm。为了模拟准确,将料仓上部划分六等分,每隔4 m设置一环梁,共六道环梁,环梁截面为400 mm×400 mm。
2 分析结构的选取及模型的建立
2.1 材料参数的选取
拟结合某石化公司脱气及储存料仓-框架结构项目,已知料仓外径为7 216 mm,内径为7 184 mm,铝合金的弹性模量为7.0×104N/mm2,钢筋混凝土的弹性模量为3.25×104N/mm2,相邻柱中心水平间距为2 546 mm,间隔柱中心水平间距为3 600 mm,不计柱本身惯性矩。
料仓-框架结构主要包括上部料仓,下部框架结构及其附属设施,其长×宽×高为45 m×18 m×39 m,如图2所示。该结构由两排十个单料仓-框架组成,料仓直径7.2 m,仓壁厚度0.16 m,料仓高度24 m,锥底部分高度8 m,框架部分长度9×5=45 m,宽度9×2=18 m,高度分两层,底层高6.2 m,二层高8.8 m。
该料仓-框架结构设计主要使用铝合金、钢筋和混凝土,材料的力学性能参数见表1。

表1 材料的力学性能参数

图2 料仓实际结构图Fig.2 Actual structure of silo

表2 结构有限元分析模型单元

图3 结构的有限元建模Fig.3 Finite element modeling of structures

图4 柱环梁尺寸、道数的调整后的有限元模型图Fig.4 Finite element model drawing after adjusting the size and number of beams
2.2 有限元模型的建立
模型验证选取单料仓框架进行分析,在建立料仓-框架结构有限元分析模型时,忽略接管、法兰、预埋套管等附属设施,有限元模型各部分单元选取见表2。
料仓仓底部按固定约束端处理,采用自底向上的建模方式建模。首先定义关键点,然后连接线段、绘制成面,再生成三维实体模型。原单料仓-框架结构和单柱环梁-框架结构有限元模型如图3所示。
2.3 柱环梁的调整
利用刚度等效公式,计算得出柱环梁的截面尺寸宽×高为400 mm×400 mm,根据本工程需要,设计以柱环梁道数为六道,将料仓上部划分六等分,每隔4 m设置一环梁。同时建立截面500 mm、600 mm尺寸柱环梁-框架结构有限元模型,与原模型进行对比分析。同时分别建立四道柱环梁、六道柱环梁和八道柱环梁的柱环梁-框架结构有限元模型,进行对比分析研究。尺寸为400 mm的柱环梁模型如图4所示。
3 结构自振特性分析
由表3可知,原料仓-框架结构模型自振频率为1.783 8 Hz,柱环梁尺寸为400 mm时,柱环梁框架结构自振频率为1.310 2 Hz,柱环梁尺寸调整为500 mm时,柱环梁框架结构自振频率为1.530 3 Hz,柱环梁尺寸调整为600 mm时,柱环梁框架结构自振频率为1.472 7 Hz。因此,在柱环梁尺寸为500 mm时,与原模型自振特性更为接近。
设定柱环梁尺寸为500 mm,调整柱环梁道数。柱环梁道数分别选取为4道、6道和8道,柱环梁道数不同情况下的结构自振频率如表4所示。由表4可知,当环梁道数为六道时,柱环梁框架结构自振频率(1.530 3 Hz)与原料仓-框架结构模型自振频率(1.783 8 Hz)最为接近。
经过以上计算得知,柱环梁-框架结构在柱环梁道数为六道,环梁截面尺寸为500 mm时更接近原模型。与刚度等效公式计算结果对比,确定刚度等效增大系数为1.25。
4 地震作用下结构响应分析
4.1 地震波的选取
本文选取了EL-Centro波、Taft波和人工波SHM2波[19]三种地震波对模型结构进行地震响应分析。根据抗震规范对底部剪力的要求,对选用的地震波峰值数据进行调幅。
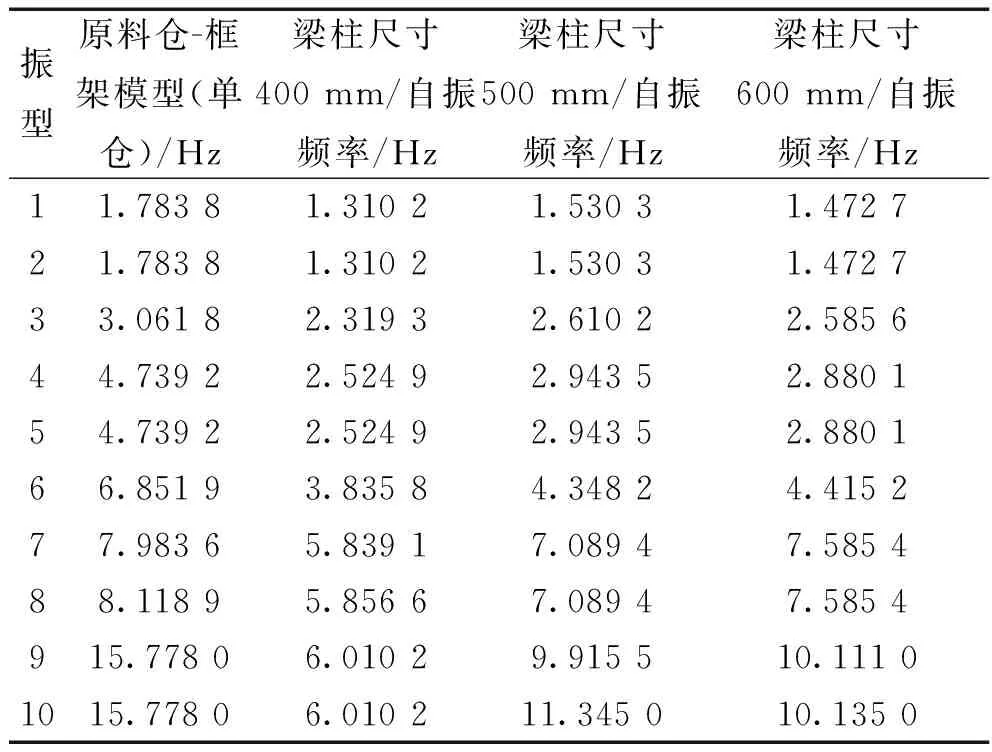
表3 不同尺寸柱-环梁结构的自振频率
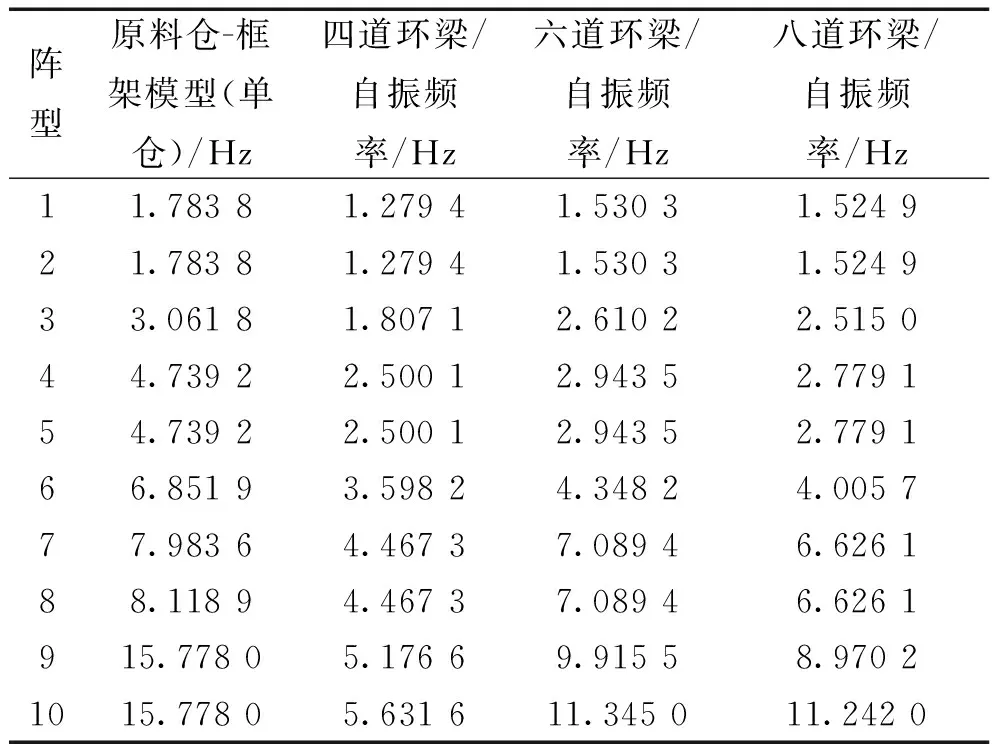
表4 不同道数环梁下结构的自振频率
4.2 地震波的调整与施加
根据文献[19],结合料仓-框架结构基本情况,拟采用地震波参数如下:EL-Centro波,间隔0.02 s,持续时间53.76 s,加速度峰值出现在第2.14 s,峰值为341.7 cm/s2,场地土属Ⅱ-Ⅲ类,时程曲线和幅值谱曲线如图5所示;Taft波,间隔0.02 s,持续时间54.40 s,加速度峰值出现在第3.72 s,峰值为175.9 cm/s2,场地土属Ⅱ类,时程曲线和幅值谱曲线如图6所示;地震波SHM2,间隔0.02 s,持续时间78.64 s,加速度峰值出现在第13 s,峰值为35 cm/s2,场地土属Ⅳ类,其时程曲线和幅值谱曲线如图7所示。
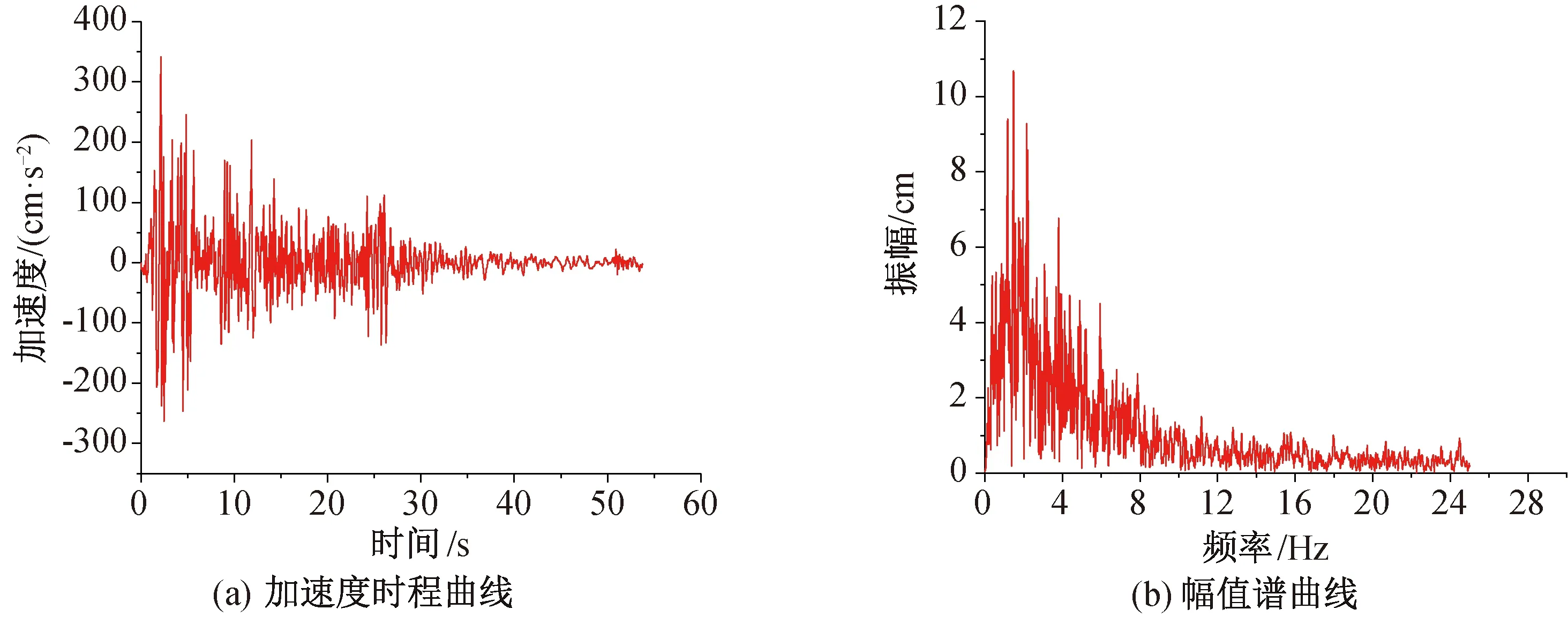
图5 EL-Centro波Fig.5 EL-Centro wave
图6 Taft波Fig.6 Taft wave
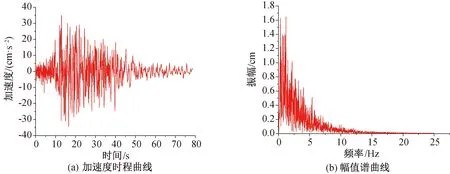
图7 SHM2波Fig.7 SHM2 wave
地震波选取后,根据自己的工况设计,进行地震波的调整,地震波加速度值调整的基本原则是:实际的地震波峰值和时程分析法采用的地震波峰值相等,如式(1)所示,选取料仓-框架结构所在地区设防烈度为7度(设计加速度峰值为0.35 m/s2)。
(1)

根据抗震设计规范推荐的方法,对加速度地震波的持续时间进行压缩。一般压缩的时间为第一次达到该加速度地震波最大峰值的10%时计起,到最后一次达到该加速度地震波最大峰值的10%结束,且压缩后的时间一般为结构基本周期的5~10倍。本文中输入的EL-Centro波、Taft波和人工波SHM2波持续时间均为25 s。
4.3 结构位移与应力响应分析
采用时程分析法,输入调整后的天然波EL-Centro波、Taft波和人工波SHM2波,对柱环梁-框架结构有限元模型进行地震作用下的动力响应分析。在7度多遇水平地震动加速度作用下,得出柱环梁-框架结构位移与应力响应,如图8所示。
通过分析可知,在EL-Centro波作用下,柱环梁-框架结构最大位移为9.85 mm,出现在柱环梁顶部,柱环梁-框架结构最大等效应力为4.73 MPa,出现在结构柱底;在Taft波作用下,柱环梁-框架结构最大位移为11.67 mm,出现在柱环梁顶部,柱环梁-框架结构最大等效应力为2.64 MPa,出现在结构柱底;在人工波SHM2波作用下,柱环梁-框架结构最大位移为4.35 mm,出现在柱环梁顶部,柱环梁-框架结构最大等效应力为1.28 MPa,出现在结构柱底,表明结构环梁顶部是比较薄弱的部位,位移最大;结构柱底受力最大,应采取积极的保护措施。不同高度下结构的应力位移变化,见图9所示。
5 结论
1)利用刚度等效原则,计算得出与实际结构刚度等效的柱环梁尺寸为400 mm。通过调整柱环梁尺寸及道数,以获得和原结构有相同自振特性的模型结构。考虑环梁尺寸影响,分别建立400、500、600 mm不同尺寸的柱环梁-框架结构模型,考虑环梁道数,分别建立四道柱环梁、六道柱环梁和八道柱环梁的柱环梁-框架结构模型,通过与原料仓-框架结构自振特性对比分析,得出柱环梁尺寸为500 mm、柱环梁道数为六道时,模拟结果最为接近原模型。在此基础上,进而确定刚度等效增大系数为1.25。
2)采用时程分析法,分别考察设防烈度为7度情况,在天然波EL-Centro波、Taft波和人工波SHM2波3种地震波作用下,柱环梁-框架结构地震响应。得到3种工况下,柱环梁-框架结构的最大位移与最大等效应力响应。柱环梁-框架结构最大位移出现在柱环梁顶部,结构受力最大位置出现在柱底,并且位移和应力变化较为均匀,建议实际设计中,应对该部位进行加强处理。

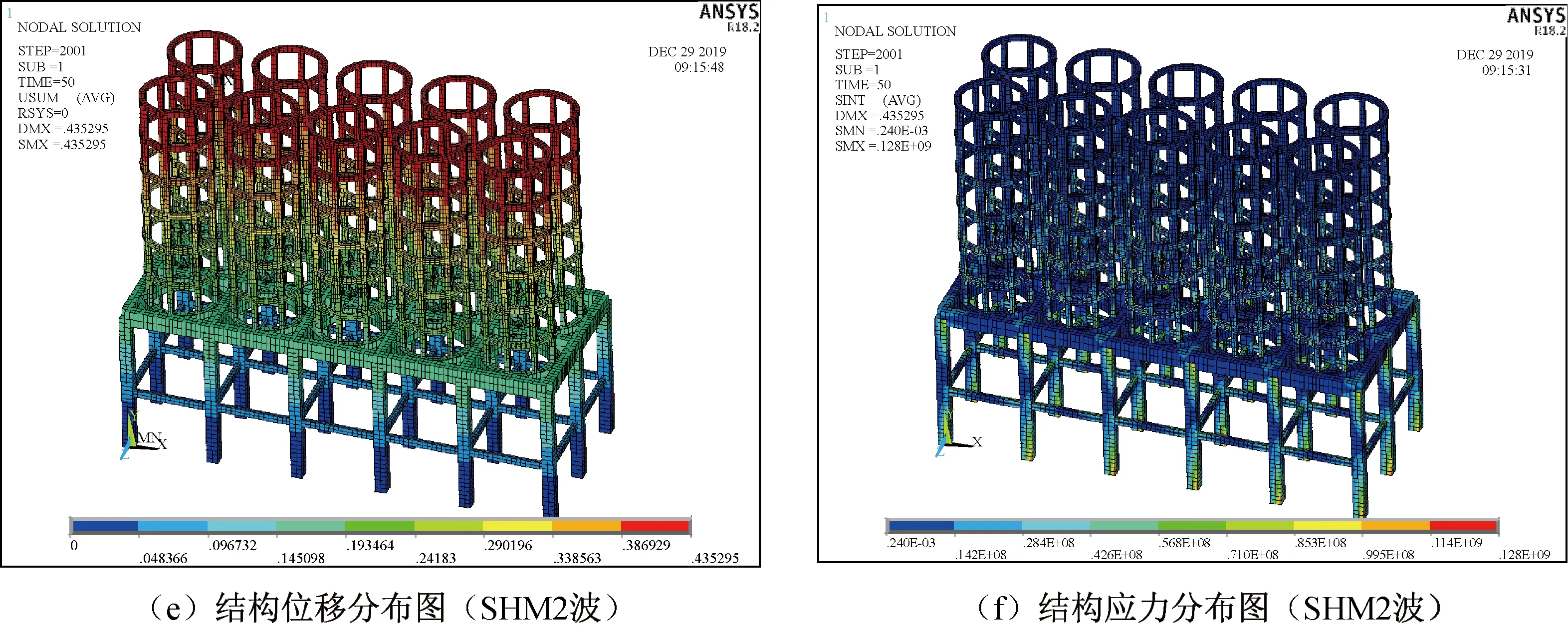
图8 结构的位移与应力分布图Fig.8 Structural displacement and stress distribution diagram
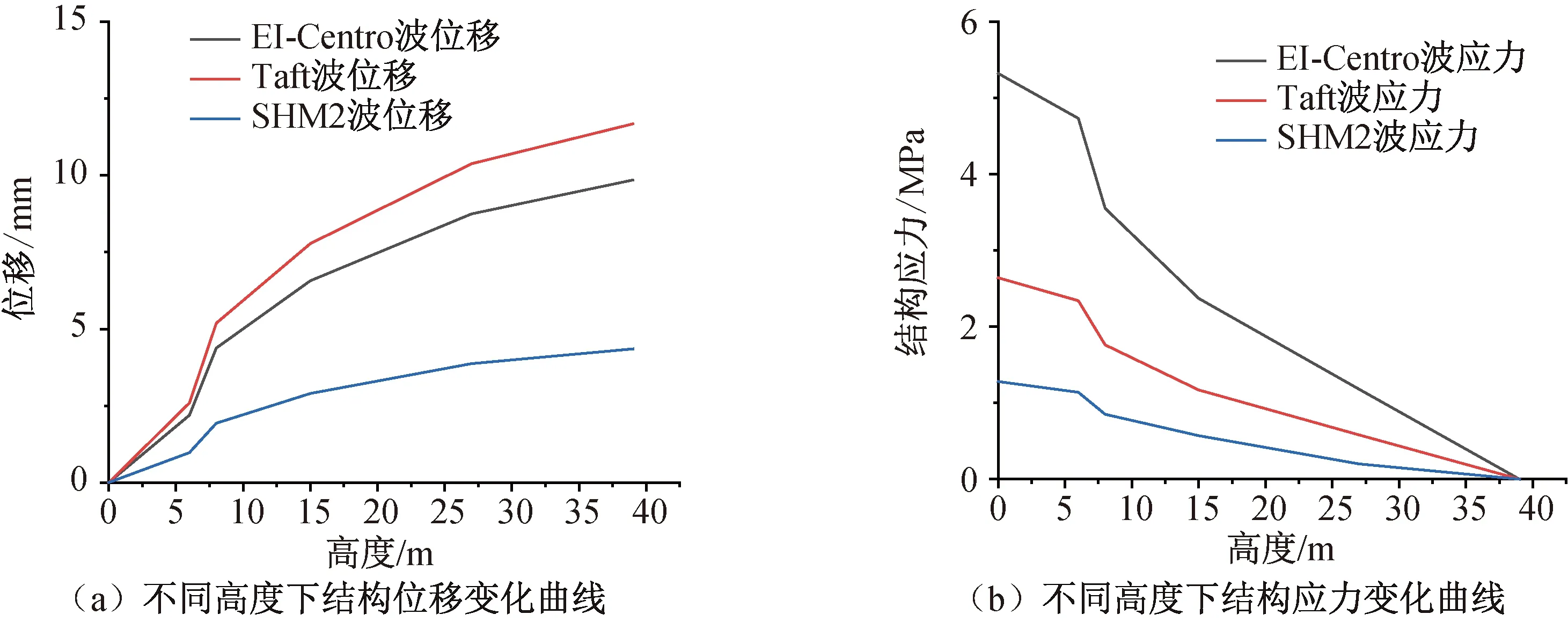
图9 不同高度下结构位移和应力分布图Fig.9 Structural displacement and stress distribution under different heights
