基于代理模型的储煤仓三心圆柱面屋盖气动外形优化研究
2021-05-10李剑鸿伞冰冰
李剑鸿,邱 冶,伞冰冰
(河海大学 土木与交通学院,南京 210098)
三心圆柱面屋盖是大型储煤仓常见的一种结构形式,具有净空高、跨度大、经济性好等优点[1]。随着我国国民经济的迅速发展,为满足存储和作业空间的需求,大型储煤仓的高度和跨度日趋增加,风荷载已成为结构设计人员不可忽视的问题。柱面屋盖是大跨度储煤仓的主要结构形式。迄今,诸多学者对柱面屋盖的抗风性能及其影响因素进行了研究。Qiu等[2]通过风洞试验研究了矢跨比和雷诺数对柱面屋盖气动特性的影响,并提出了一种基于改进势流理论的平均风压模型。Johnson等[3]对矢跨比为0.27~0.5的柱面屋盖风荷载特性进行了雷诺数效应研究,发现屋盖的雷诺数敏感性随矢跨比的增加而增大。Li和Ding等[4-5]通过刚性模型测压试验获得了矢跨比为1/3和1/5的柱面屋盖表面的压力分布,研究发现屋盖迎风面的压力随着矢跨比的增大而显著减小。基于风洞试验数据,单鲁阳[6]和齐月芹等[7]分别采用0.618法、穷举法和数学规划法中的复形法对双层柱面网壳的矢高、网格尺寸和网壳厚度进行了结构优化分析。三心圆柱面屋盖的气动特性与其几何外形密切相关,但针对这类结构的气动外形优化研究甚少。本文将基于代理模型和数值模拟技术,对三心圆柱面屋盖结构进行气动外形优化研究,以获得最优的形状设计参数,为大跨度储煤仓的抗风设计提供参考。
1 CFD数值模拟
以张雷[8]风洞试验的三心圆柱面屋盖作为数值模拟的Benchmark模型,该模型的矢高和跨度分别为H=200 mm、S=540 mm,中间圆弧的半径为350.6 mm、圆心角为61.32°,两端圆弧的半径为187.3 mm、圆心角为54.34°,缩尺比为1∶200。选用标准k-ε、RNGk-ε和SSTk-ω三种湍流模型对柱面屋盖周围的绕流流场进行数值模拟,并与风洞试验数据进行对比验证。计算域的长度和高度为10 800 mm×2 000 mm,模型位于距来流入口约1/3计算域长度处,图1为计算域示意图。采用非结构化网格进行网格划分,网格总数量约为15万,屋盖近壁面处网格尺寸为Δx=S/80、Δz=H/20,其表面y+值约为30~60。图2为屋盖附近的网格划分情况。边界条件具体设置见表1。

图1 计算域示意图Fig.1 Schematic diagram of computational domain
通过数值模拟获得的屋面平均风压分布与风洞试验结果对比如图3所示。由图可知,标准k-ε和SSTk-ω湍流模型在屋盖尾流区的模拟结果与试验数据偏差较大,而RNGk-ε湍流模型则具有较高的模拟精度,故选用该湍流模型进行三心圆柱面屋盖的气动外形优化研究。

图2 屋盖周围网格划分Fig.2 Grid system near the roof

图3 屋面平均风压分布的数值模拟与风洞试验结果对比Fig.3 Comparison of the mean pressure coefficients on the roof surface between numerical simulation and wind tunnel test
2 屋盖气动优化模型
图4为三心圆柱面屋盖几何模型示意图。屋面由半径为R、圆心角为q的中间圆弧,和半径为R1、圆心角为q1的两端圆弧组成。假定中间圆弧与两端圆弧在其交点处的切线重合,则三心圆柱面屋盖的几何参数满足如下关系式:
(1)
(2)
其中,参数C1和C2可由下式计算得到:
(3)
(4)

表1 计算域边界条件

图4 三心圆柱面屋盖几何模型示意图Fig.4 Schematic diagram of geometry model of the three-centered cylindrical roof
强风作用下柱面屋盖顶部可能会产生较大的风吸力,致使其发生风致破坏。本文分别以三心圆柱面屋盖的负压峰值最小、竖向位移绝对值最小为优化目标,以屋盖中间圆弧的半径与跨度之比(R/S)和圆心角(θ)作为优化变量,对其进行气动外形优化,以获得最优的形状设计参数。所以,三心圆柱面屋盖的气动外形优化是一个单目标、多变量的优化问题,优化模型表达如下:
minF1(R/S,θ)=max{|Cpi|},
(5)
minF2(R/S,θ)=max{|Wi|},
(6)
式中:F1(R/S,θ)和F2(R/S,θ)为目标函数;Cpi为屋面第i个点的平均风压系数;Wi为屋面第i个点的竖向位移值。优化变量R/S的上下限分别为lR=0.52和uR=1.48,其中R/S=0.52时,为单心圆柱面屋盖,而当R/S>1.48时,屋盖几何外形变化较小;圆心角θ的上下限分别为lθ=0°和uθ=2arcsin(0.5/(R/S)),其中θ=2arcsin(0.5/(R/S))时,两侧小圆弧起点和终点连线AB垂直于地面。有限元模型采用双层网壳结构形式,基本参数如下:网壳跨度和高度分别为108、40.26 m,厚度为3.5 m。采用圆钢管杆件,其长度为4 m,杆件截面尺寸为159 mm×10 mm。
3 优化结果
三心圆柱面屋盖负压峰值的预测曲面如图5所示,由图可知,目标函数F1与设计变量之间存在着复杂的非线性关系。如图6所示,研究结果表明,kriging代理模型的预测值与目标函数真实值(CFD模拟)的最大误差为4%,该代理模型可以构建较为精确的预测曲面。图5中C1点为最优解,得到R/S=1.26,θ=45.8°,相应的屋面负压峰值|Cp|max=0.84(位移值|W|=4.665 mm),与初始形状相比,屋盖负压峰值降低了约17%。图7为最优解C1对应的屋盖表面平均风压分布,与其附近参照点C2 (R/S=1.26,θ=20°)和C3 (R/S=0.93,θ=45.8°)工况的对比图。由图可见,优化后的屋盖顶部风吸力值明显减小,而尾流区的变化不显著。
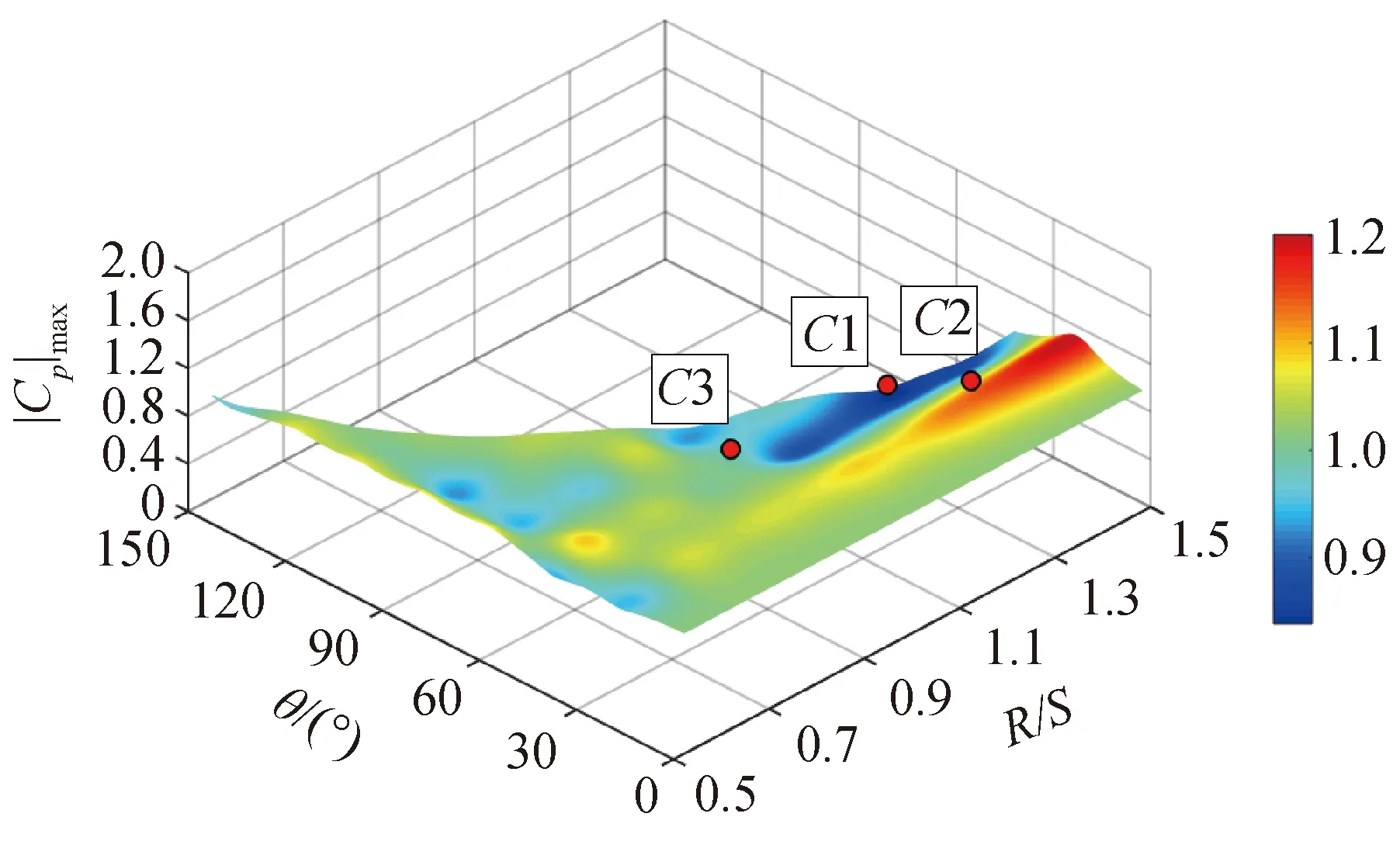
图5 负压峰值的kriging模型预测曲面Fig.5 kriging model prediction surface of negative pressure peak
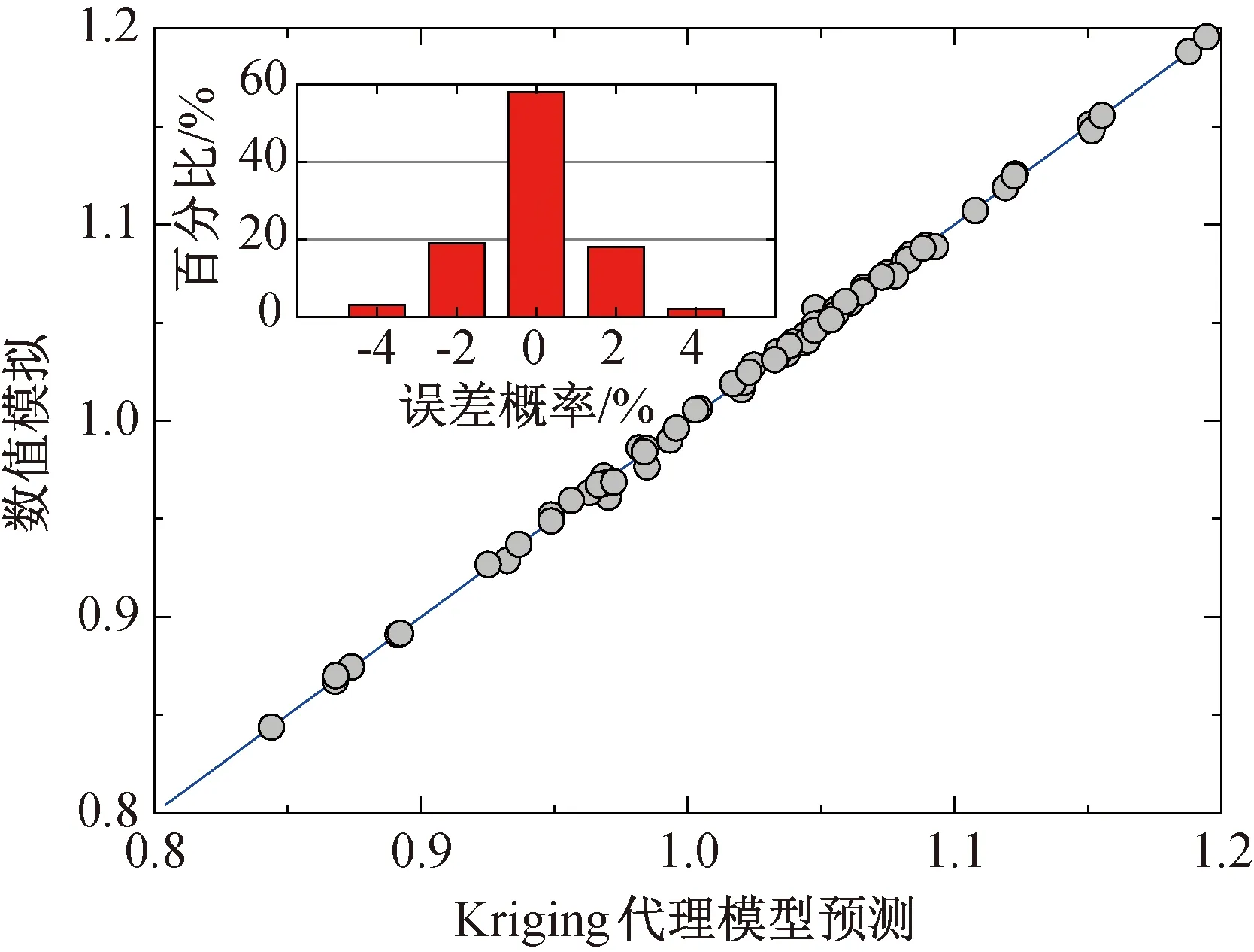
图6 负压峰值优化的kriging代理模型的预测值与目标函数真实值的对比图Fig.6 A comparison diagram of the predicted value of the Kriging agent model optimized by peak of negative pressure and the real value of the objective function
图8为双层柱面网壳竖向位移极值的预测曲面。图中W1点为最优解,得到R/S=0.56,θ=14.1°,相应的网壳竖向位移值|W|max=0.293 mm(负压绝对值|Cp|=0.95),与初始形状相比减小了近55 %。最优解W1与参照点W2(R/S=1.3,θ=20°)和W3(R/S=0.56,θ=120°)对应的屋盖竖向位移分布如图9所示,由图可见位移极值位于网壳顶部区域,具有最优外形的三心圆屋盖能够明显减小其竖向位移极值。

图7 最优解C1与参照点C2、C3对应的屋盖表面平均风压分布图Fig.7 Mean pressure distributions on the roof surface with optimal (C1) and near optimal (C2 & C3) shapes
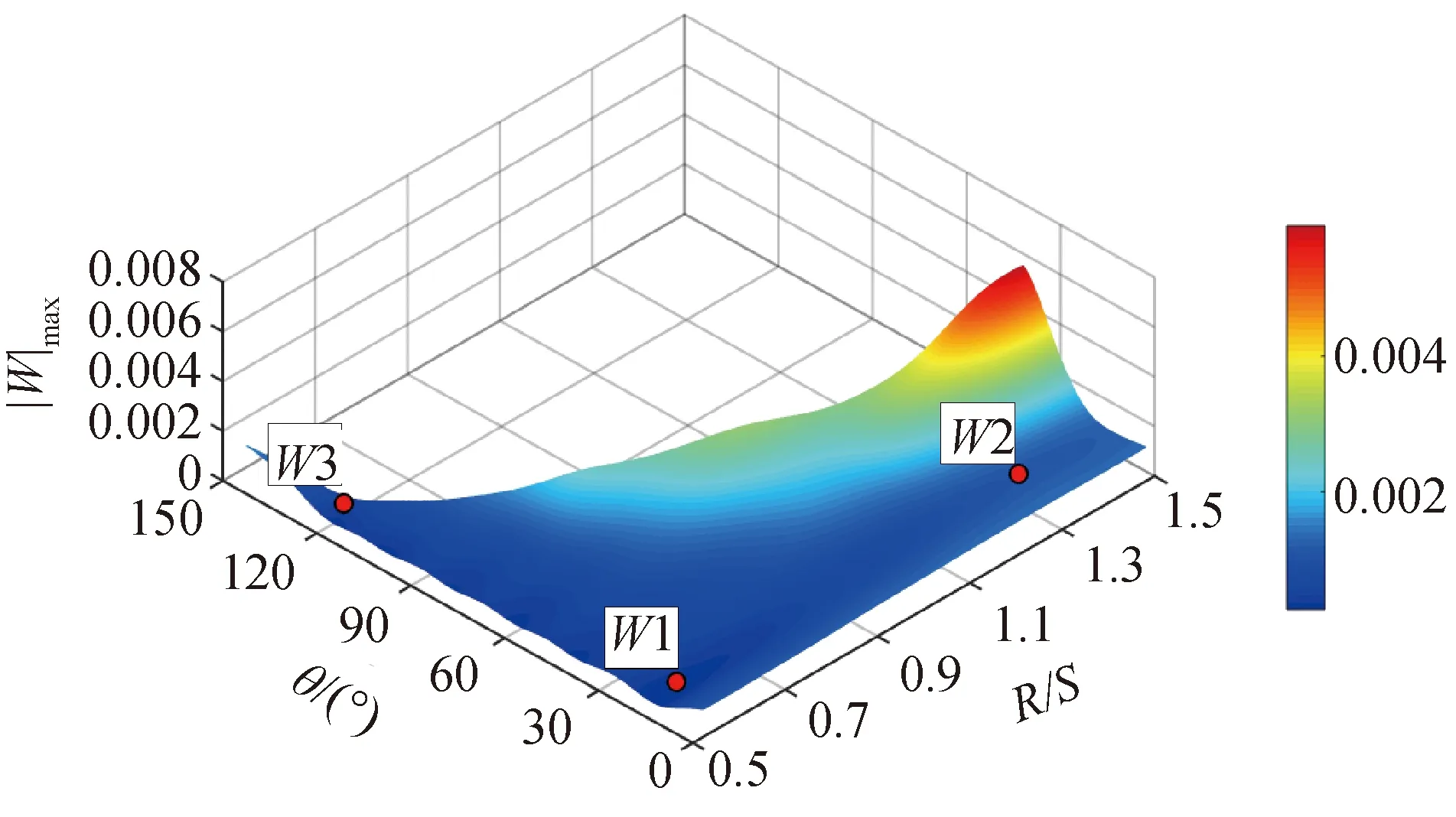
图8 竖向位移极值的kriging模型预测曲面Fig.8 kriging model prediction surface of vertical displacement extremum

图9 最优解W1与参照点W2、W3对应的屋盖竖向位移图Fig.9 Vertical displacement distributions of roof with optimal solution (W1)and reference points (W2 & W3)
4 结论
1)通过风洞试验数据对数值模拟算例进行了验证,研究发现RNGk-ε湍流模型具有较好的模拟精度。
2)基于kriging模型建立了三心圆柱面屋盖气动外形优化的代理模型。结果表明,当R/S=1.26,θ=45.8°时,屋面的负压峰值为|Cp|max=0.84;当R/S=0.56,θ=14.1°时,双层柱面网壳的竖向位移极值为|W|max=0.293 mm。
