灌区干支渠渗漏估算方法及其在水资源优化配置中的应用

张 帆，蔡宴朋，郭 萍，谭 倩，王 烜

（1. 北京师范大学环境学院水环境模拟国家重点实验室，北京 100875； 2. 广东工业大学环境生态工程研究院，广东省流域水环境治理与水生态修复重点实验室，广州 510006；3. 南方海洋科学与工程广东省实验室（广州），广州 511458；4. 中国农业大学水利与土木工程学院中国农业水问题研究中心，北京 100083）

0 引 言

由人口增加与气候变化等因素引起的水资源短缺危机威胁着中国的粮食安全与生态健康。如何提高农业生产中水资源利用效率以促进区域可持续发展，将是未来一段时间内中国农业水利领域需要解决的主要问题。而在农业灌溉过程中，干支渠的渠道渗漏是造成灌溉水损失的重要原因之一[1]。因此，准确估算干支渠的渠道渗漏对于指导渠道工程建设与制定有效农业水资源优化配置方案均具有重要意义。

渠道渗漏估算的研究主要有现场试验、经验公式、理论公式、数值模拟[2]共4类。这些研究从不同角度揭示了渠道入渗的机理与过程，为估算不同研究尺度、不同衬砌条件下渠道渗漏提供了有效方法。但在解决实际工程问题时，通常要求估算方法具备结构简单，参数较少的特点。例如在实际渠道工程设计规划中，相较其他方法，公式结构简单、参数数量少的经验方法[3]获得了更广泛应用。而现有对于渠道渗漏量计算常用的经验公式，如针对有衬砌渠道的Davison-Wilson公式、针对土渠的Kostiakov公式与Molesworth公式等通常是以单位长度渠道为研究对象，研究尺度较微观，更适合单条渠道设计使用。而对于农业水资源规划的研究，依据研究对象与研究尺度可以分为流域尺度、灌区尺度、渠系尺度、田间尺度[4]。目前仅在田间、渠系研究尺度下尝试构建耦合了多参数的公式[5-7]。现有的渠道渗漏公式在处理如多灌区、多区域这类较大尺度水资源配置应用时仍然存在参数数量较多且难以获得的问题。另外，这些方法与水资源优化模型耦合时难度较大，会造成优化模型求解困难。因此农业水资源配置相关研究中通常使用不同渠道的渗漏系数来粗略估计渠道渗漏损失[8]。使用渠系渗漏系数方法来估算渠系渗漏量虽然避免了应用复杂估算方法时存在的参数与尺度问题，但是这种简化方法建立在渠首引水量对于渠道渗漏系数基本没有影响的假设上。然而几乎所有有关渠道渗漏量的研究中均提及水深、流速等水量要素对于渠道渗漏系数有直接的影响[9]。因此，有必要联系已有的渠道渗漏估算方法，提出更符合渠道渗漏形成机理、更适合大尺度水资源管理应用的渠道渗漏估算方法，为农业水资源的精细化管理提供支持。

农业水资源配置往往借助具体优化模型来获得规划方案。国内外对于农业水资源优化模型的研究方向主要包括模型构建与求解方法[10]、多目标多尺度协同调控[11-12]、不确定性表征[8]、优化-模拟耦合[13]、网格尺度建模[14]等。这些研究不仅加深了对于农业水资源配置系统的认识，也为农业水资源优化配置提供了有效决策工具。然而，在流域尺度、灌区尺度的水资源优化配置研究中，受渠系渗漏计算公式的复杂度所限，现有的较大尺度研究不能在规划目标中考虑更多渠道信息。因此，需要在提出的渠道渗漏估算新方法基础上，将更多影响渠道输水效率的因素纳入到农业水资源优化配置框架，考虑渠道渗漏动态变化构建水资源优化配置模型，以期在农业水资源规划中更好反映渠道输水效率并获得更准确的水量信息，提高优化配置方案的有效性和可行性。

综上，本研究将在考虑影响渠道渗漏形成要素的基础上，结合统计模型针对大中型灌区干支渠提出结构简单、参数较少的渠道渗漏估算公式，并尝试将其用于实际的灌区水资源优化配置中，构建农业水资源多目标随机规划模型。以中国典型干旱内陆河区——甘肃省黑河中游的17个大中型灌区为研究对象，与固定渠道渗漏系数方法进行对比来说明不同渠道渗漏量计算方法对于水资源优化配置结果的影响，以期为农业水资源高效利用提供有效决策工具。

1 大中型灌区干支渠渗漏估算方法构建

通过总结渠道渗漏经验公式涉及因素，发现主要包括渠床土壤组成与结构、渠道断面形式及水力特性、地下水埋深、渠道长度、渠道衬砌条件[2,7,15-16]。Zhang等[17]发现，对于某一区域内的干支渠道，渠首引水量、衬砌渠道长度、无衬砌渠道长度与渠道渗漏量存在以下多元回归关系：

式中a、b、c为多元回归的系数；W为渠首引水量，m³；LD为衬砌渠道长度，km；ND为无衬砌渠道长度，km；CL为渠道渗漏量，m³。

Zhang等[17]虽然发现这些参数具有很好的回归关系，但并未进一步从渗漏发生机理方面进行解释。式（1）中的渠首引水量为整个规划期的引水量，代表了渠道的引水能力，引水能力的大小体现了渠道断面和水力特性的综合影响。而衬砌渠道长度与无衬砌渠道长度可以表征渠道长度与衬砌条件的影响。另外，在研究某个地下水埋深较深的特定区域时，通常认为渠床土壤类型变化不大，且地下水埋深对于渠道渗漏的影响较小。综上，可以认为式（1）能够应用于地下水埋深较深的区域渠道渗漏量的估算。此外，由于渠道长度和衬砌率是更常用到的参数，将式（2）和式（3）代入式（1），整理后得到式（4）的形式。

式中TD是渠道总长，km；β为渠道衬砌率。

基于以上公式，在水资源优化配置中常用的渠系水渗漏系数（δ）可以表示为[2]式中W净为渠道向田间输水总量，m³；W毛为渠道引水总量，m³。

为进一步明晰渠道引水量与渗漏系数的关系，以渠道引水量W为自变量对式（5）进行求导，可以获得以下关系：

由式（6）可知，渠道渗漏系数与渠道引水量的关系取决于(c+(b-c)·β)的正负，而不是简单的线性关系。当(c+(b-c)·β)＜0时，δ′(W)＞0，渠道渗漏系数为渠道引水量的单调增函数；当(c+(b-c)·β)=0时，δ′(W)=0，渠道渗漏系数与渠道引水量的变化无关；当(c+(b-c)·β)＞0时，δ′(W)＜0，渠道渗漏系数为渠道引水量的单调减函数。以上函数关系表明，在渠道引水量变化时，渠道渗漏系数不随渠道引水量变化是一种特殊情况，使用固定的渠道渗漏系数可能会高估或者低估渠道渗漏的损失。本文将通过以下农业水资源优化配置实例来进一步说明这个问题。

2 渠系渗漏估算方法在水资源规划中的应用

2.1 研究区概况

黑河流域（98°～101°30′E，38°～42°N）是中国典型干旱内陆河区，降水较少且蒸发强烈。黑河中游地区灌溉农业发达，是中国重要的农业生产基地。近年来，由于该区域人口增加、工业发展、农业生产规模扩大，水资源需求持续增加，导致中游与下游生态用水减少，流域生态健康受到严重威胁[18]。此外，黑河中游灌区渠道工程情况与水资源短缺程度不相适应。根据2016年张掖市水利统计年报，截止到2015年底，黑河中游甘州区、临泽县、高台县共有干支渠16 908条，总长2 810 km，干支渠的衬砌率不到60%，渠系水资源利用率约为60%。为缓解流域水资源供需矛盾，助力流域可持续发展，黑河中游农业节水化发展势在必行。黑河中游农业水资源绿色高效利用问题已经引起了广泛关注，学者们也建立了很多水资源优化配置模型尝试合理分配有限灌溉水资源[5,19-21]。将本文渠道渗漏系数估算方法应用于中国甘肃省黑河中游地区的17个灌区间的水资源优化配置问题中，与在水资源配置中广泛使用的渗漏系数方法进行对比以检验其有效性。灌溉水资源优化配置中的渗漏系数在测量渠首入渠水量与渠末输出灌溉水量后通过式（5）获得。

2.2 优化模型构建

灌区水资源优化配置是包含多决策目标、多重不确定性的复杂系统问题。为了在决策中协调多决策目标，反映系统中的主要不确定性特征，不确定性多目标优化模型被广泛用于解决此类问题。本文考虑地表径流随机性与农业生产效益、效率等多个目标，建立了灌区水资源多目标优化配置模型，并参考Li等[7]求解多目标模型使用的最小偏差法，通过最小化各目标函数与其最优取值之间的偏差获得多目标模型的解。优化模型构建如下：

1）目标函数

① 最大化净效益

② 最大化灌溉水使用率

③ 最大化灌溉水生产力

其中EBik，IWUEik，IWPik由以下公式计算得到

2）约束条件

① 地表水可供水量约束

② 配水连续性约束

③ 地下水可供水量约束

④ 粮食安全约束

⑤ 需水约束

⑥ 非负约束

式中i、t、k分别为灌区、月份、水文年的编号；TEB、TIWUE、TIWP分别表示总净经济效益（元）、总体灌溉水使用率（%）、总体灌溉水生产力（kg/m³）；pk为不同水文年发生概率；EBik、IWUEik、IWPik分别表示k水文年i灌区净经济效益（元）、灌溉水使用率（%）、灌溉水生产力（kg/m³）；Bi、Yi、YAi分别代表灌区i单位面积效益（元/kg）、单方水产量（kg/m3）、单位面积产量（kg/hm2）；CSMi、CGMi分别为i灌区地表水、地下水管理费用，元；CSW、CGW分别代表地表、地下水供水费用，元；Aik表示i灌区k水文年的灌溉面积，hm2；EPitk为k水文年i灌区t月有效降雨量，m3；ηik为i灌区k水文年的渠系水利用系数；σi为灌区i的田间水利用系数；SWAitk、GWAitk分别为i灌区t月k水文年的地表、地下水可利用量，m3；TSWAik、TGWAik分别为i灌区k水文年总地表、地下水可用水量，m3；Si(t-1)k和Si(t-2)k分别为i灌区t-1月和t-2月k水文年的余水量，m3；FD为最小人均粮食需求量，kg/人；POi、IRi分别为灌区i的人口与最小净需水量，m3；SWitk、GWitk分别为i灌区t月k水文年的地表、地下水优化配置量，为i灌区t-1月k水文年的地表水余水量，m3。

2.3 数据来源

本文以甘肃省黑河中游17个灌区（包括大满灌区、盈科灌区、西浚灌区、上三灌区、安阳灌区、花寨灌区、平川灌区、板桥灌区、鸭暖灌区、廖泉灌区、沙河灌区、梨园河灌区、友联灌区、六坝灌区、罗城灌区、新坝灌区、红崖子灌区）的主要灌溉时期（4—9月）的灌溉水资源配置为研究对象。将莺落峡水文站 1944—2019年连续76 a径流序列进行P-Ⅲ曲线配线，并根据水文频率P划分特丰水年（VH，P≤15.0%）、丰水年（H，15.0%＜P≤37.5%）、平水年（M，37.5%＜P≤62.5%）、枯水年（L，62.5%＜P≤85.0%）、特枯水年（VL，P＜85.0%）5个水文年。不同水文年供需水量、种植面积可以在Li等[7]研究中获得。农产品市场价格、不同水源用水成本从张妍等[22]研究中获得。下面将针对渠道渗漏相关参数的收集与处理进行介绍。

首先需要确定区域渠系水利用估算公式中参数。通过调研收集了2015年甘肃省全部82个大中型灌区中的77个灌区内渠道总引水量与渠道总长、衬砌率与渠系渗漏系数如表1所示。表2展示了黑河中游17个灌区的渠道建设基本情况，这些参数将通过式（5）代入到优化模型中来反映不同灌区渠道的渗漏情况。借助EXCEL数据分析功能中回归分析模块，使用甘肃省77个大中型灌区的渠道引水量、渠道总长、渠道衬砌率进行多元线性回 归计算。

表1 甘肃省77个大中型灌区组渠道总引水量、总长、衬砌率与渗漏系数Table 1 Total water diversion, total length, lining rate and leakage rate of canals in 77 large and medium-sized irrigation areas of Gansu Province

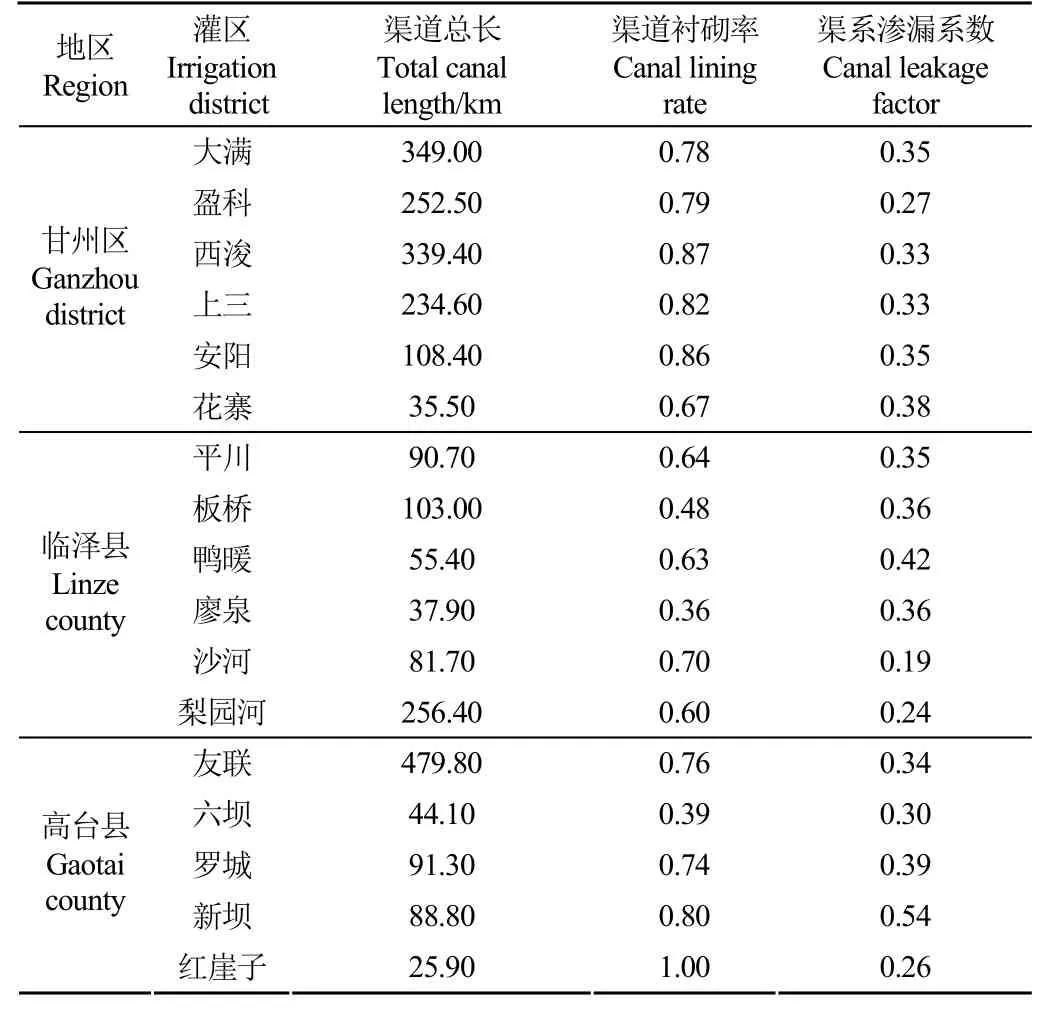
表2 黑河中游灌区渠道基本情况Table 2 Canal condition of irrigation districts in the middle reaches of Heihe River

3 结果与分析

3.1 灌区模型构建结果

模型拟合结果如表3所示。图1展示了渠道渗漏量观测值与使用多元回归方法获得的模拟值对比。可以看出回归结果的置信度与决定系数较高（R2=0.95）表明获得的参数精度与可信度较高。从图可以看出，模型可以较好模拟不同引水规模下渠道渗漏损失，可以认为获得的渠道渗漏量估算模型能够反映甘肃省内大中型灌区内干支渠渗漏情况。模型回归系数a为0.419，b为-1.587，c为0.927。

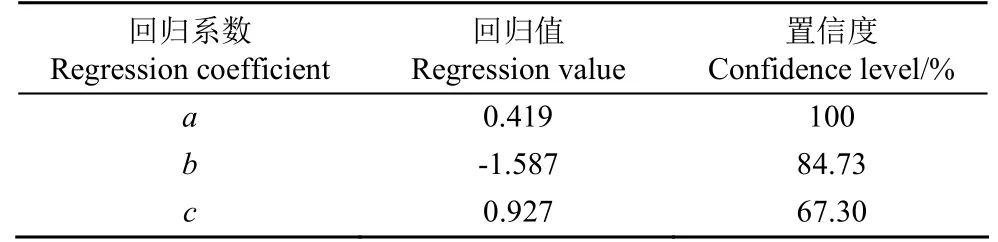
表3 渠道渗漏估算模型回归结果Table 3 Regression results of canal leakage estimation model

3.2 多目标模型权重确定

求解多目标模型需要确定各目标的权重。本研究使用层次分析法基于目标的两两比较构建判断矩阵，检验判断矩阵一致性后，确定净效益（目标一）、灌溉水使用率（目标二）、灌溉水生产力（目标三）的权重分别为0.6、0.2、0.2。在LINGO软件中对所建立的优化模型进行编程，输入优化模型参数后获得基于本文提出的渗漏量估算方法的水资源优化配置结果（表4）。

由表4可知，由于选择的不同典型水文年降雨量不同，同一个灌区同一月份在不同水文年的配水量有显著差别。总体上来看，灌溉水总量从特丰水年到特枯水年有增加趋势，地下水在总灌溉水量中所占比例逐渐增加。

为详细比较使用本文提出的渗漏系数估算方法与传统渗漏系数方法对于灌溉水资源优化配置的影响，进一步计算这2种配水结果的总渗漏量、水分生产力、水分利用率（渗漏损失水量/总水量）与经济效益配水指标，计算结果如表5所示。由表可知，2种方法在优化配水指标上有明显差异。尤其对于渗漏量的估计，相较传统的固定渗漏系数方法，二者偏差在10%以上，使用本文提出的渗漏系数估算方法得到的渠道渗漏量随不同水文年变化更为明显，可以反映出渠系渗漏系数随渠首引水量变化的动态规律。2种方法得到的水分生产力均在平水年达到了最高值，这表明：1） 当灌溉可用水量过少时，会影响作物产量导致水分生产力下降；2）当灌溉水量增加到一定程度时，继续增加灌溉水量虽然会提高粮食产量，但是产量增加速度放缓，同样会导致水分生产力降低。这提醒着农业水资源管理者需要关注作物产量与水量的边际效益关系。此外，虽然配水指标显示，固定渠系渗漏系数方法有更高的水分利用率和经济效益，但由于对于田间作物实际可用水量估计的误差，这可能会导致这些配水指标并不能真正实现。

为直观对比2种方法应用于农业水资源优化配置中渗漏系数差异，表6给出了2种方法下不同水文年各灌区的渗漏系数变化。可以发现，对于不同水文年地表可用水量比较敏感的灌区，如大满灌区、盈科灌区、西浚灌区、梨园河灌区，渠系渗漏系数也有相应的变化，而固定系数不能反映渠道渗漏率随渠首引水量变化的动态响应关系。而且，固定渗漏系数的方法对于大部分灌区的实际渗漏系数有所低估，这可能是因为渠道渗漏系数测算时的渠道引水量相较实际优化中引水量偏小导致的。

4 结 论

针对较大尺度农业水资源规划渠道渗漏系数不能反映实际渗漏过程的问题，基于前人的相关研究，提出了一种干支渠渗漏系数估算方法。研究表明，渠道渗漏系数与渠道引水量之间存在动态函数关系而不是简单的线性关系。仅使用渠系水利用系数或渗漏系数来计算渠道渗漏量不能反映渠首引水量变化导致的渗漏系数动态变化，进而影响农业水资源规划中对于可用田间灌溉水量判断。

为验证以上假设，将提出的渠道渗漏估算方法应用于甘肃省黑河中游17个灌区间水资源多目标优化配置的实际案例中，并与传统的固定渗漏系数方法进行了对比。从灌区间农业水资源优化配置的对比中可以发现，传统的固定渗漏系数方法虽然可以在水资源优化配置中反映渠道渗漏对于可用水量的影响，但当渠道引水量发生改变的时候，固定系数方法不能反映渗漏系数的动态同步变化。这可能会导致对渗漏量的估计产生10%以上的偏差，进而影响实际的田间可用水量、预期产量、预期收益的估计，影响农业水资源优化配置方案的实用性与有效性。本研究是基于统计数据提出的，若能够结合现场试验的方式进行验证，将会大大提高其普适性。因此，未来应当结合更多现场试验与观测资料，进一步完善渠系渗漏估算方法，为农业水资源精细化管理提供有效工具，助力农业节水化发展。