鸡胚疫苗注射时蛋壳力学模型分析及参数优化

2021-05-09王红彬赵明岩胡剑虹王宗炼宋天月刘弘业李运良陶伟鹏

农业工程学报 2021年4期

王红彬，赵明岩，胡剑虹，王宗炼，宋天月，刘弘业，李运良，陶伟鹏

（中国计量大学机电工程学院，杭州 310018）

0 引言1

中国是肉鸡生产和消费大国，生产量与消费量仅次于美国居世界第二位[1]。目前中国每年需要免疫的种鸡超过50亿羽，免疫密度达80%以上。近年来鸡胚接种技术[2-3]迅速发展，已被30多个国家使用，美国有超过90%的肉鸡孵化场使用自动化蛋内注射系统，用以接种马立克病（MD）疫苗、新城疫苗等，极大地提高了鸡胚免疫效率[4]。随着人工成本的增加，国内也逐步采用自动化设备取代手工注射。但采用自动化设备接种鸡胚时，针头的冲击会使鸡胚（胚蛋壳）产生裂纹，导致免疫失效甚至死蛋现象[5]，裂纹造成的废胚率高达4%～5%。

采用侧孔针头击穿蛋壳并将免疫液注入是鸡胚接种的关键。因此，必须对蛋壳受到针头冲击时的力学特性进行分析。国内外对蛋壳力学特性的研究分静力学[6-10]（对蛋壳进行压缩、拉伸、承压等试验，研究蛋壳抗压缩、抗变形能力，弹性模量等）与动力学[11-15]（振动、跌落和碰撞等）两个方面。李硕等[16]采用ANSYS软件对鸡蛋模型进行了静力学分析，得出了鸡蛋蛋壳受力变形和破碎的规律；Zhang[17]对鸭蛋进行压缩试验，并采用有限元分析法模拟了蛋壳的静载力学性能，证明尖端承受压力大于钝端；Priyadumkol等[18]采用反求法和有限元分析法确定蛋壳的力学性能；Ketelaere等[19]研究了鸡蛋无破坏性冲击产生的振动频谱，以此评价蛋壳特性及最低频率响应时产生的三维振动模型，并分析了鸡蛋动态硬度值与蛋壳赤道处宽度、厚度、形状指数的相关关系。Zhao等[20]通过对鸡蛋壳的不同点进行机械冲击，通过动态频率响应可实现蛋壳裂纹检测，旨在为食用鸡蛋在加工、包装和运输等方面提供理论指导。但上述研究均未涉及尖锐刚体刺穿蛋壳的相关试验。

本文对接种时的胚蛋壳进行动力学特性研究并建立力学模型，通过ANSYS有限元分析验证该模型，搭建试验装置并设计正交试验，寻找裂纹率最低的注射参数，从而降低鸡胚接种的废胚率。

1 蛋壳力学模型与分析

1.1 结构分析

鸡蛋外形一般可分为三部分：大头为钝端，小头为锐端，横向最长距离处为赤道。不同种类和地区的鸡蛋外观存在差异，鸡蛋外形一般可近似采用拟椭圆曲线[21-22]来描述。即

式中a为长半轴，mm；d为短半轴，mm；φ为蛋形角，（°）；将（1）式转化成参数方程为

式中x、y分别为拟椭圆曲线边缘横纵坐标；是指椭圆曲线赤道处点A(d,0)的斜率的反切值，根据（2）式可绘出蛋壳模型，如图1所示。

选取江西吉安7～14日胚龄乌鸡样本孵化种蛋100枚，用数显游标卡尺（量程：0～150 mm，精度：0.03 mm）测量长轴、短轴，经冷光源照射，测出气室面积（长轴方向气室投影面积）和气室轮廓长度，测量完后将此100枚种蛋敲碎，取蛋壳钝端部分，去除内皮后晾干，用测厚规测量钝端厚度，测量数据如表1所示。

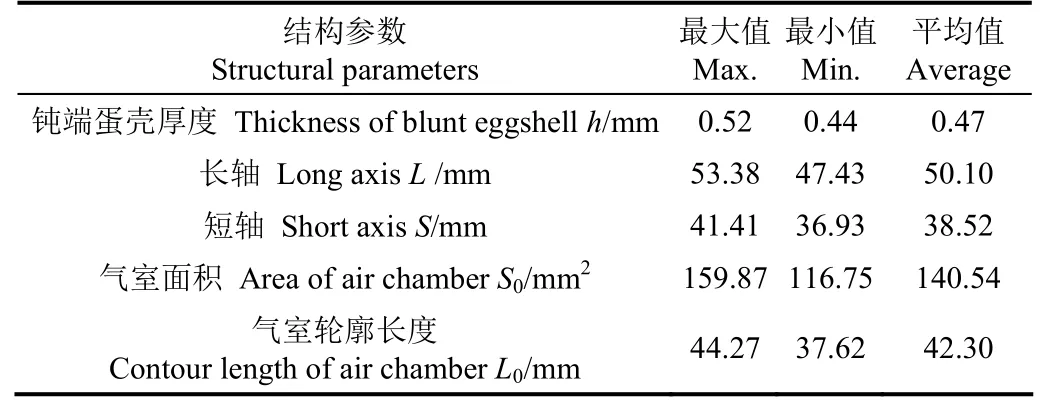
表1 7～14日龄鸡胚外观参数测定Table.1 Measured parameters of 7 to 14 day's embryo

1.2 力学模型建立

鸡胚接种时，注射部位除羊膜腔之外，胚蛋的气室、卵白、卵黄囊、尿囊均可作为有效注射部位[23]。对7～14日胚龄鸡胚通过气室注射的外源物质易于被吸收，可降低注射液体对胚胎的应激，不易出现机械损伤，注射操作较为简单。本研究对鸡胚钝端气室进行注射，建立注射时蛋壳的力学模型。

设针头刺穿蛋壳的最大作用范围的半径为Ar，注射体系质量（与注射针头相连的所有物体质量之和）为m，针头穿过蛋壳后距接触点o的距离为x处针头的瞬时速度为v，针头刚接触蛋壳的初速度为v0，如图2a所示，由动量守恒定律有

式中M t(x)为针头穿过蛋壳后距接触点o的距离为x处的蛋壳体系的动量。注射区域蛋壳的平均厚度为h，蛋壳密度为ρ，距离针头柱体轴线为s的圆环上的点，经针头冲击后，该点发生了竖直方向的位移ξ，其坐标为(r,)ξ，如图2a所示，此时圆环的动量为

式（4）中'ξ为所选取微元的速度

对式（4）积分可得

采用侧孔针头，针头形状为锥形，针头足够尖锐时，式（6）中rmin≈ 0。针头冲击蛋壳时，距离针头柱体中心为r的圆环（r≤R，取R= 0.75 mm ）的瞬时速度与针尖瞬时速度相同，则针头刺入过程中产生蛋壳碎块的有效质量可定义为

由式（3）和（4）可得

蛋壳的结构由外壳、蛋壳膜和壳内皮组成（图2b）。针头刺入过程中断裂的小块壳体仍依附在蛋壳内皮上，未随针头飞落入气室中，距刺入点o长度为s的微元，形成壳碎片后到刺入点o的距离仍为s，即

针头锥形部位穿过蛋壳，注射动作即可完成，此时

由式（6）和（10）可得

根据冲量定理[24]，可知与针头接触的圆环对针头的轴向合力为

而单位长度针孔根部圆周的轴向力为

由图2a中的几何关系可知

由式（5）和（14）可得径向速度为

若注射孔共产生n个断裂壳碎片，每个碎片的质量可定义为

每个碎片的径向动量为

同时可求出每个碎片所受的径向合力Fy为

则针孔根部圆周上单位长度所受的径向力fb及合力f分别为

合力的方向与注射方向所成的夹角为θ'，如图2b所示。

将（11）代入（20）中可得

式中f为蛋壳注射孔根部单位长度所受合力，N；ρ为蛋壳密度，kg/m3；m为注射体系质量，kg；v0为注射初速度， m/s-1；β为针头锥形角，(°)；R为针头柱体半径，mm。

由式（21）可知注射孔单位长度所受合力f与蛋壳密度ρ、蛋壳厚度h、注射体系质量m、注射初速度v0、针头锥形角β有关。正常孵化的鸡胚的蛋壳密度ρ和厚度h会略微变小，便于雏鸡啄壳。本研究选用的样本为7～14日胚龄鸡胚，ρ和h的变化很小，视为定值。

1.3 注射时蛋壳有限元分析

为验证1.2节建立的力学模型的正确性、缩小注射参数范围，同时进一步探索鸡胚注射过程中蛋壳变形量、应力应变随锥形角、注射初速度及注射体系质量的变化关系，采用ANSYS软件对针头冲击蛋壳过程进行仿真分析。

蛋壳结构复杂，宏观上是一个薄壁体，其主要成分是CaCO3。假设蛋壳是均匀、连续、各向同性的[25]。蛋壳强度主要取决于壳体，其内膜、蛋内容积物对蛋壳强度影响很小，在研究中可忽略。

使用ANSYS workbench中显性动力学（Exlicit Dynamics）模块，在geometry中导入Solidworks已建蛋壳模型，垂直于鸡胚钝端注射。测得鸡胚长轴均值L为50.10 mm，短轴均值S为38.52 mm，钝端厚度均值h为0.47 mm，蛋形角φ取10°；样本蛋壳弹性模量和泊松比[26-27]平均值分别为E=27.85 GPa，μ=0.28，密度为2 532 kg/m3。针头采用结构钢材料，密度为7 850 kg/m3。网格划分时，蛋壳采用正四面体单元，元素尺寸设为0.002 mm，针头采用三维六面体的Solid95单元，元素尺寸设为0.001 mm。目前使用的侧孔针头，锥形角通常为5°、10°、15°，但5°针头柱体半径较小，刚度及强度较低，不适合注射蛋壳等硬度较大的材质，因此只需考虑10°和15°锥形角的针头。添加Total Deformation模块和Equivalent Stress模块可求解出蛋壳注射孔变形量以及注射孔根部所受应力。

1.4 受力分析结果

由1.2节建立的力学模型（式（21））可知，影响注射孔根部单位长度所受合力f的主要因素有3个。采用单一变量法，改变其中一个因素，另外两因素做组合，可绘制出f与注射初速度、针头锥形角及注射体系质量的变化关系，如图3所示。

由图3a可知，蛋壳注射孔单位长度所受合力f随针头注射初速度v0的增大而增大，且注射体系质量m和针头锥形角β越大，f增大速度越快；不难看出，f也随β、m的增大而增大。

根据1.3节鸡胚注射有限元分析，可得图4所示针头冲击鸡胚蛋壳不同穿刺状态下的应变云图。针头未刺穿时，蛋壳应变较小（图4a），蛋壳能恢复部分变形；针头恰好刺穿时，蛋壳有最大应变，蛋壳破损较为严重（图 4c）；在能刺穿蛋壳情形下，通过调整注射参数，可使蛋壳变形最小（图4b）。

改变注射初速度v0，可得蛋壳变形量及所受应力与v0的关系曲线（见图5）。图5b的总体变化趋势与图3b一致，可验证力学模型的准确性。由图5a可知，在v0= 0.4 m/s 附近，蛋壳变形量较大，此时蛋壳未被刺穿。v0增大后，针头刺穿蛋壳，在v0= 0.6 m/s 附近，变形量较小。图5b所示，v0增大时，蛋壳所受应力也在增大。相比其他组合，采用（β=10° ，m= 0.5 kg ）及（β=10° ，m= 1.0 kg ）组合，蛋壳注射孔变形量及所受应力较小。综合图5的数据，v0的范围选在0.5～0.8 m/s较为合适。

改变注射体系质量m，可得蛋壳变形量及所受应力与m的关系曲线（见图6），由图6b可知，蛋壳所受应力随m的变化趋势与图3c一致，进一步验证了力学模型的准确性。当m＜ 0.3 kg 、v0＜ 0.4m/s时，蛋壳未刺穿；当m＞ 0.3 kg、v0≥0.4 m/s ，针头刺穿蛋壳。在m= 1.0 kg、v0= 0.6 m/s附近，有较小变形量。当m＞ 1.0 kg、v0＞ 0.6 m/s 后，蛋壳变形量与所受应力逐渐增大。综合图6的数据，m的范围选为0.5～1.2 kg较为合适。

由ANSYS软件分析可初步确定注射初速度v0的范围为0.5～0.8 m/s，注射体系质量m的范围为0.5～1.2 kg，针头锥形角β为10°、15°。

2 鸡胚注射参数优化试验

2.1 计算机视觉技术检测注射孔裂纹

精准识别注射孔裂纹是参数优化的关键，注射后的鸡胚，通过肉眼难以察觉微小裂纹，容易造成误判。计算机视觉技术在裂纹检测方面应用较多[28-29]，成本较低，且易实现。本研究采用计算机视觉技术对鸡胚注射孔裂纹进行检测，检测步骤为：第一步：对相机进行位置标定（使用带显微功能的SNO745-10A系列CCD彩色相机），对注射后的鸡胚背部进行冷光源打光操作，采集图像（图像格式为PNG，位深度为24bit），如图7a、7b所示；第二步：图像去噪，为最大程度上去除图像噪声，同时保留注射孔裂纹细节部分。非线性滤波器能较好滤除脉冲干扰及扫描噪声，同时保留轮廓边缘信息，使用中值滤波器（Median Filter）和双边滤波器（Bilateral Filter）对鸡胚注射孔区域图像进行滤波，通过对照发现双边滤波效果较好，滤波效果如图7c；第三步：对滤波后的图像进行阈值分割，通过试验发现，阈值为135时，能保留全部裂纹特性，但大部分亮斑无法消除，影响检测效果；当阈值从135增到173时，虽去除部分亮斑，但裂纹特征不能有效保留；当阈值大于173时，则无法测得全部裂纹特征。阈值为135和173时效果图如图7d、7e所示。

第四步：采用传统阈值方法的分割效果不理想，本文提出一种鸡胚亮斑消除算法，对阈值为135的二值化图像进行形态学开运算，可完整保留裂纹特征，对开运算后的图像进行Blob连通域检测，统计连通域标记点数i（i=1,2,3,...），计算每个连通域最小外接矩长边im、短边ni及连通域面积Si，找到最大连通域面积Smax即为注射孔像素面积，同时计算每个连通域圆形度C（iCi=mi/ni，圆形度Ci≈1，则连通域趋于圆形；Ci＞＞1时，连通域越趋于线条形）。当Ci＞C0时，则为有效裂纹，应保留；若Ci＜C0且Si＜Smax时，则为亮斑，应填充。通过试验发现，圆形度C0=3时去除亮斑效果最好。图8所示为网状、线性、无裂纹鸡胚亮斑消除效果。

第五步：对有效裂纹进行像素累加计算，可得鸡胚注射孔有效裂纹像素面积和有效裂纹轮廓长度，由于相机位置已标定，可求得注射孔有效裂纹实际面积和有效裂纹实际轮廓长度。

2.2 裂纹蛋与完好蛋的判别指标

图9a、图9b分别为完好蛋胚及裂纹蛋胚。为保证试验均一性和可靠性，定义裂纹有效面积指数SΔ 和裂纹有效长度指数LΔ 两个参数，以此来判别鸡胚是否注射成功。计算式分别为

式中P为有效裂纹实际面积，mm2；Q为有效裂纹实际轮廓长度，mm；R为针头柱体半径，mm；0L为气室轮廓长度，mm；S0为气室面积，mm2。

随机选取注射失败的鸡胚，通过计算机视觉技术测量出注射孔有效裂纹实际面积及有效裂纹实际轮廓长度，取多组测试平均值分别为：P= 19.60 mm2，Q= 12.56 mm 。根据表1中测量的数据可知L0= 42.30 mm ，S0= 140.54 mm 。

根据式（22）、式（23），当 ΔS≥ 12.69%或 ΔL≥18.56%时，即可被识别为裂纹鸡胚；当 0＜ΔS＜ 12.69%且0 ＜ΔL＜ 18.56%时，可判别为完好鸡胚。

2.3 试验装置与方法

为确定鸡胚注射最优参数，搭建了试验装置，试验装置集成了高速摄像机测速单元、注射系统、缓冲机构及鸡胚注射孔裂纹检测装置，如图10所示。

选取针头锥形角度1x，注射体系质量x2，注射初速度3x，3个因素进行正交试验，求解注裂纹率最小的参数组合，根据预试验选取各个因素的水平值，如表2所示。

表2 正交试验因素水平Table 2 Factors and levels of orthogonal tests

2.4 试验结果与分析

选用L8(27)正交表安排试验[30]，共8组，每组试验重复100次，统计其注射成功率（每组中，注射后完好鸡胚数量与总鸡胚数量之比）。设试验注射成功率结果为Y1，Y2，…，Yn，对所用正交表的第j列（包括空列），令Kjl为第j列中相应于水平l（l=1,2, …,r）的m个试验结果之和。正交试验结果如表3所示。

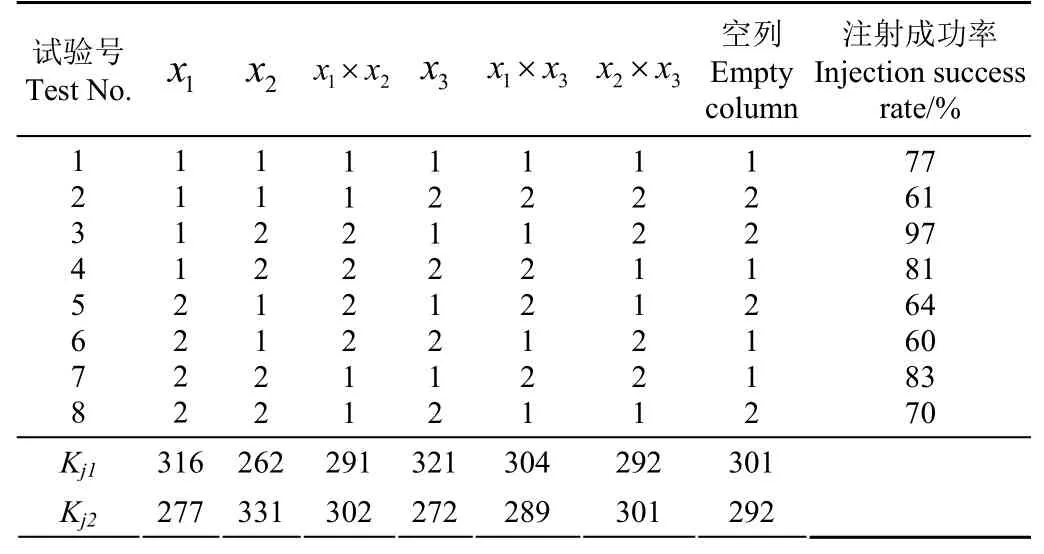
表3 正交试验结果Table 3 Results of orthogonal tests

查表得临界值为：F0.9（01，1） = 39.9，F0.95（1，1）=161.4，F0.99（1，1） = 4052。列出方差分析，如表4所示。

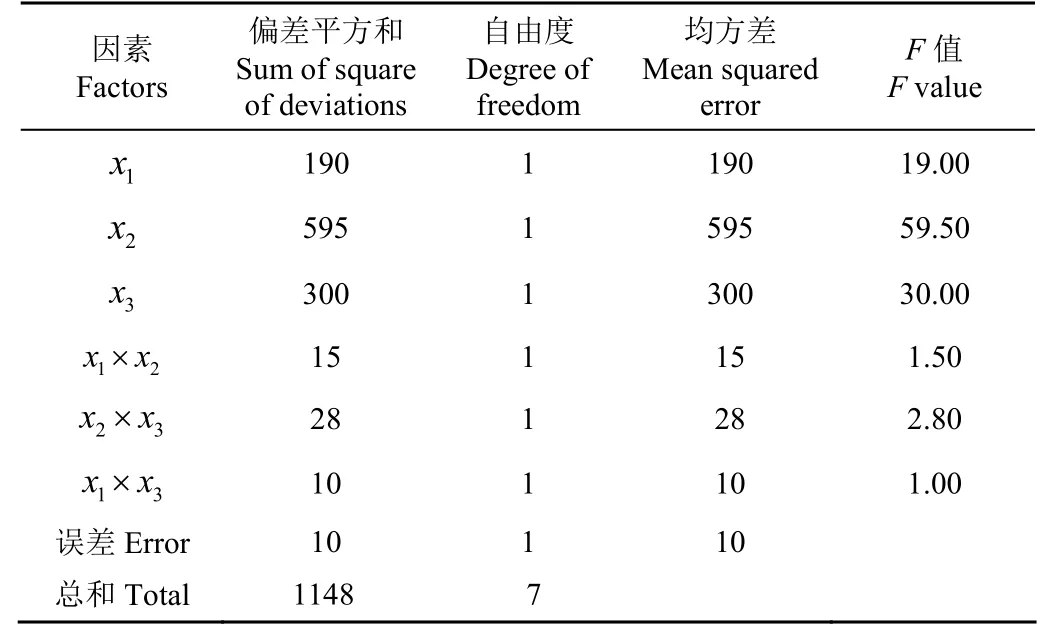
表4 正交试验方差分析Table 4 Analysis of variance for orthogonal experiment

由表4可知，Fx1×x2、Fx2×x3、Fx1×x3的值很小，表明交互作用x1×x2、x2×x3、x1×x3是影响注射成功率的次要因素，交互作用不显著。将交互作用项的平方和与自由度合并到误差项中，重新查出临界值可得：F0.9（01， 4） = 4.54，F0.95（1， 4） = 7.71，F0.99（1， 4）=21.20，得到修正后的方差分析表如图表5所示。

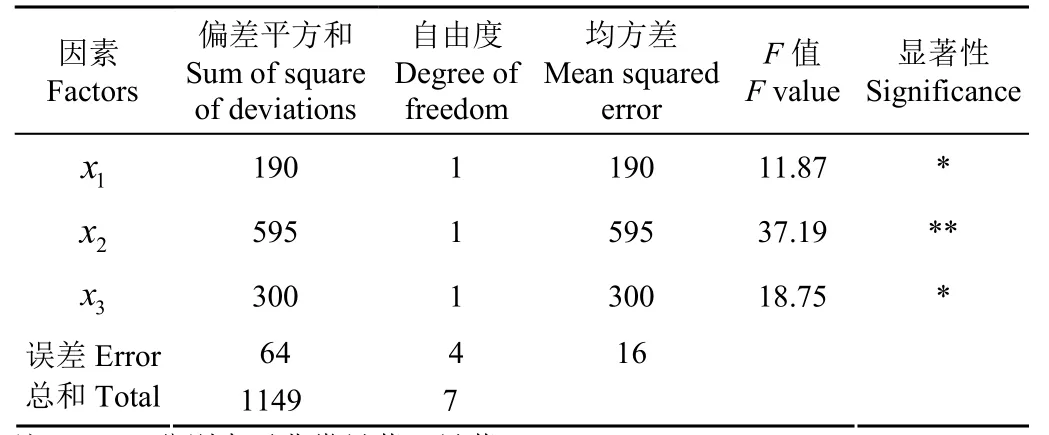
表5 修正后的方差分析Table 5 Modified ANOVA

由图表5可知，显著性水平：Fx2＞Fx3＞Fx1，即鸡胚注射时，对蛋壳产生裂纹的作用影响大小分别为：注射体系质量m、注射初速度v0和针头锥形角β。对于因素x1、K11＞K12，故较优水平为x11；对于因素x2，由K22＞K21，故较优的水平为x22；对因素x3，由K31＞K32，故较优水平为x31；因此最优注射参数组合为：x11x22x31。即针头锥形角10°、注射体系质量1.0 kg、注射初速度0.6 m/s。采用江西吉安乌鸡样本种蛋80枚，进行优化参数组合试验，注射成功率为98.75%。