基于降维双谱分析法的航空发动机轴承磨损故障分析

王艳丰，郜伟强，滕光蓉，敬发宪，何 伟

(中国航发四川燃气涡轮研究院，四川绵阳 621000)

1 引言

航空发动机承力传动系统中，轴承起着承受及传递载荷的作用，其运行状态对整个发动机的工作状态有着直接的影响。航空发动机轴承因承力模式复杂、工作条件苛刻、工作状态多变等，极易在运行过程中出现故障。一旦发生故障，轻则导致发动机转子系统振动异常，重则造成转子抱死、发动机空中停车，甚至造成机毁人亡的严重事故[1-3]。为此，对航空发动机轴承进行状态监测和故障诊断是其研制过程中必须攻克的一项技术，同时该技术对降低飞机维修费用、减少飞行事故也具有十分重要的意义。

航空发动机轴承状态监测和故障诊断的主要方法有振动监测分析、温度监测分析、滑油光谱监测分析等。其中，融入了信号分析方法的振动监测不仅能实时在线监测发动机轴承的运行状态，还可实时进行轴承故障定位，因此备受轴承研制和使用人员的青睐。但传统的信号分析方法，如傅里叶变换，是一种局限性的变换，很难分析非平稳含噪信号。近年来，随着小波理论的发展，大量学者将小波分析法应用到轴承故障诊断中。如韩磊等[2]利用小波包频谱对带内圈、外圈和滚动体故障轴承的实测振动信号进行分析，有效判定了轴承故障并识别了单点故障发生的具体位置。梁先芽等[4]利用小波变换和包络谱分析相结合的方法，成功提取了主轴轴承故障信息并进行了故障诊断。卢艳辉等[5]应用小波包分解与重构算法分离出滚动轴承的故障特征频率，识别出滚动轴承的故障类型。尽管小波分析法在轴承故障诊断中得到大量的应用，但其也有缺陷，如易受信号传递路径的影响，且需预先降噪处理。航空发动机轴承振动信号多由安装在发动机承力机匣上的振动传感器拾获，其包含了复杂的传递路径信息，且富含噪声[6]，若采用小波分析方法对航空发动机轴承信号进行分析，将面临降噪、分析结果精确度等问题。

双谱分析技术是近年迅速发展起来的数字信号处理技术，它能有效分离和提取信号中的特征谱，自动抑制噪声，是处理非线性、非高斯信号的强有力工具[4]，但双谱分析技术的计算量较大，对设备的硬件要求较高。本文对双谱进行对角切片处理形成降维双谱，并利用降维双谱对某型航空发动机轴承故障振动数据进行具体分析，有效提取了发动机轴承故障特征信息。

2 降维双谱的基本原理

功率谱是信号自相关函数的傅里叶变换。与此类似，双谱是信号的二阶累积量的多维傅里叶变换，是处理非线性、非高斯含噪信号的有力工具，理论上具有抑制噪声、分辨率高、能获取相位信息和检测二次相位耦合频率等优点[7-8]。

2.1 双谱

设x(t)为离散、平稳、0 均值的随机过程，其三阶累积量为：

式中：τ1、τ2为时延，E{·}代表数学期望。

假设R3x(τ1,τ2)满足绝对可和条件，则双谱可定义为三阶累积量的二维傅里叶变换，即式(1)的二维傅里叶变换：

根据双谱的定义和高阶累积量的性质可知，经过双谱的高斯信号恒为0，因此双谱能够描述信号的高斯性和对称性[9]。此外，双谱从更高阶概率结构表征随机信号，弥补了功率谱不包含相位信息的缺陷，能定量描述非线性耦合。由于发动机振动信号中的噪声一般近似当作加性高斯随机噪声，其双谱等于0，因此应用双谱对发动机振动信号进行分析可以很好地抑制噪声。

2.2 降维双谱

双谱属于高阶谱，其计算量相对一般频谱方法的大，如果将双谱直接引入工程在线实时数据分析中，将给硬件系统带来负担。为此，在工程中往往对其进行降维处理，即对三阶累积量直接进行对角切片，再对对角切片进行一维傅里叶变换。对公式(1)进行变换处理得到的降维计算式如下：

式中：X(ω)为x(t)的傅里叶变换，X*(ω)为X(ω)的复共轭。

根据公式(3)可以得到，降维双谱有以下性质[10-11]：

(1) 设x(t)为0 均值、基频是ω0的n次实谐波信号，在幅值A相等、相位为0 的情况下，当 |ωm|＜ |ωl|(ωm=mω0，m=±1，±2，…，±n)时，有C(ωm)＞C(ωl)。此性质表明、采用降维双谱分析谐波信号时，信号的基频分量可得到加强，但这一性质中的0 相位假设在实际中是不可能的。

(2) 设x(t)为0均值的高斯噪声，则有C3n(ω)恒等于0。此性质表明降维双谱可抑制高斯随机噪声。

(3) 设x(t)为0 均值的随机噪声，任何两个不同时刻都互不相关，且概率密度函数为对称分布，则有C3n(ω)恒等于0。此性质表明降维双谱也可抑制对称分布的随机噪声。

(4) 设x(t)为谐波信号，ωm、ωp和ωq为其中3个谐波分量，若ωm≠ωp+ωq，则有C3n(ω)恒等于0。此性质表明，当信号中含有非相位耦合的谐波项时，通过降维双谱处理，谐波信号可被清除。

3 轴承磨损故障振动数据分析

最常用的航空发动机主轴轴承类型为圆柱滚动轴承，主要包含轴承外圈、轴承内圈和保持架等部件，基本结构如图1 所示[12]。发动机轴承出现故障时，会产生特征频率的冲击，引起轴承振动，且不同模式故障其特征频率也各不相同。为此，通过分析轴承振动信号，提取特征频率，可判定轴承发生故障的类别和部位。

图1 圆柱滚动轴承基本结构示意图Fig.1 Basic structure diagram of cylindrical rolling bearing

3.1 振动仿真数据分析

航空发动机的振动信号，可看成由发动机转子振动信号、其他振源信号、噪声信号混叠而成。当轴承发生故障时，混叠信号通常会出现与轴承相关的特征频率。根据发动机振动信号构成以及轴承发生故障时的特征，由计算机仿真生成一组含有噪声的轴承内圈和滚动体磨损振动数据。其中，转子转频为173.0 Hz，轴承内圈的频率为39.0 Hz，轴承滚动体的频率为87.0 Hz，数据采样点数为4 096个，采样频率为5.6 kHz/s，噪声为高斯白噪声。仿真数据的时域波形图如图2所示。对仿真生成的轴承磨损数据进行傅里叶分析，得到如图3 所示的频域幅值谱。对仿真生成的轴承磨损数据进行降维双谱分析，得到如图4所示的频域幅值谱。

图2 仿真数据的时域波形图Fig.2 Time domain waveforms of simulation data

图3 仿真数据傅里叶变换结果图Fig.3 Fourier transform results of simulation data

图4 仿真数据降维双谱分析结果图Fig4 Bi-spectrum’s dimension results of simulation data

从图2可知，当轴承发生磨损时，其振动信号时域图中存在明显冲击振动，但这种冲击振动成分基本淹没在噪声中，仅从振动信号时域很难判定轴承状态。图3 中能明显观察到39.1，87.5，173.4 Hz 频率成分，其他频率成分基本淹没在噪声中。图中的分析结果说明，对轴承磨损数据进行传统的傅里叶变换，仅能得到轴承组成部件的振动频率成分，无法判定轴承是否发生故障。图4 中除存在39.1，85.9，173.4 Hz 频率成分外，还存在134.0，212.5，259.4 Hz频率成分，其中134.0 Hz 是轴承内圈频率与转频的差频，212.5 Hz 是轴承内圈与转频的和频，259.4 Hz是轴承滚动体与转频的和频。134.0，212.5，259.4 Hz频率成分的出现，不仅说明了发动机的振动信号存在非线性耦合现象，轴承发生了故障，还可以通过调制频率成分定位故障部位为轴承的内圈和滚动体磨损。此外，图4中的噪声成分明显比图3中的弱，说明降维双谱能够很好地抑制轴承故障振动信号的噪声。

3.2 振动实测数据分析

3.2.1 轴承实测振动数据

某型航空发动机膜盘联轴器后支承使用双滚动轴承结构形式，轴承与膜片组件、传动轴直接接触。对膜盘联轴器进行静频测试，得到轴承座的一阶固有频率为215.2 Hz，膜片组件的一阶固有频率为622.0 Hz，传动轴的一阶固有频率为1 212.5 Hz。在其动态特性探究试验中，为监测膜盘联轴器轴承工作状态，在后支撑轴承座的水平、垂直方向各安装1支压电式振动加速度传感器，轴承振动信号经传感器输入到相应的数据采集系统，采样频率为12.8 kHz/s，试验全程进行数据采集。

试验中膜盘联轴器从0转速以200 r/min的速率升速到最高转速(20 000 r/min)，在最高转速状态下稳定运行3 min后，转子突然发生轴向窜动，法兰盘螺钉与支座撞击产生火星，转子系统与齿轮箱输出轴的连接尼龙绳断裂，联轴器转速迅速下降，试验停止。试验结束后对膜盘连轴器进行分解，发现两轴承的内外圈和滚动体有明显磨痕，如图5 所示。由于故障发生时试验件解体，传感器也脱离试验件，因而未获得故障时刻相应的试验数据。为此，主要以传感器脱离前的8 192 个数据点为分析对象，对这些数据进行时域、傅里叶、降维双谱分析。

图5 轴承损坏部件Fig.5 Damaged parts of bearing

3.2.2 数据分析

图6为后支撑轴承座故障前的振动数据时域波形图，图中能够明显观察到冲击信号存在，但冲击信号与噪声信号混叠，信号特征不突出，在时域信号图中很难判定轴承是否故障。

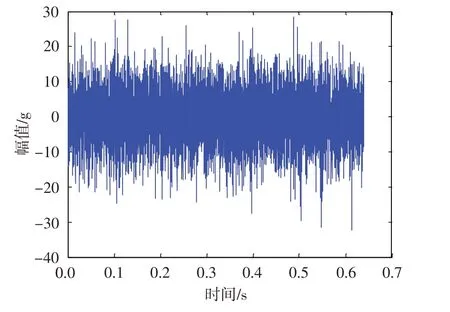
图6 轴承损坏前的时域波形图(垂直方向)Fig.6 Time domain waveform before bearing damage(Vertical)

对振动数据进行传统的傅里叶变换分析，得到如7 所示的结果。图中明显存在噪声成分，非噪声信号归一化幅值小于0.1的频率成分淹没在噪声中，因此传统的频谱分析无法获取淹没在噪声中的特征频率以及判定噪声中是否存在异常频率。图中能够观察到332.8，431.2，621.8，981.1 Hz 频率成分，其中332.8 Hz是膜盘联轴器转子基频，431.2 Hz是轴承座的固有频率的2 倍频，621.8 Hz 是膜片组件固有频率，981.1 Hz 约为转子的3 倍频，从上述频率成分无法判定轴承是否存在异常。

对振动数据进行降维双谱处理，得到如图8 所示的结果。图中噪声归一化幅值明显比图7中的小，说明降维双谱对实测数据中噪声成分具有明显的抑制作用。图中除存在332.8，431.2，621.8，981.1 Hz频率成分外，还存在117.2，143.7，189.0，215.6，549.9，864.0 Hz 频率成分，其中215.6 Hz 是轴承座的固有频率，117.2 Hz 为转子基频(332.8 Hz)与轴承座固频(215.6 Hz)的差频，189.0 Hz为膜片组件固频(622 Hz)与轴承座固有频率的2 倍频(432.1 Hz)的差频。117.2 Hz 和189.0 Hz 频率成分的存在说明，膜盘联轴器在发生故障解体前，振动信号中已经出现轴承座信号的调制信号，轴承已经存在异常。

图7 轴承损坏前的傅里叶分析图(垂直方向)Fig.7 Fourier transform results before bearing damage(Vertical)

图8 轴承损坏前的降维双谱分析图(垂直方向)Fig.8 Bi-spectrum′s dimension results before bearing damage(Vertical)

4 结论

通过对双谱进行降维处理形成降维双谱，降维双谱能够定量描述非线性信号的耦合现象，对混叠信号中的噪声具有抑制作用。将降维双谱引入到航空发动机轴承振动信号分析中，可提取轴承运行状态的特征向量。降维双谱对航空发动机轴承故障预测和诊断具有良好的效果，可推广应用到航空发动机整机试验中，对轴承状态进行在线监测和诊断。