基于双向测量的转子真实不平衡响应分析技术

2021-05-09解梦涛张霞妹张强波

燃气涡轮试验与研究 2021年5期

解梦涛，张霞妹，张强波

(中国飞行试验研究院发动机所，西安 710089)

1 引言

转子不平衡是导致转子系统故障最常见的一个因素[1-2]。对于航空发动机等复杂转子机械系统，在使用过程中因磨损等原因会导致转子不平衡量增加，诱发整机振动增大。针对此问题，民用航空发动机多配备不平衡监测与配平功能来监测转子不平衡状态、延长服役寿命，部分高精度加工机床电主轴甚至具备在线动平衡功能[3-4]。由转子动力学原理可知，在转子系统常见的不平衡、不对中、碰摩、油膜涡动等因素中，只有不平衡会激起基频振动[5-6]，且其与转子不平衡量之间基本满足线性假设原理。为此，通常将测量的基频振动直接作为转子不平衡的衡量指标[7-8]，用于状态监测，或直接作为动平衡计算的输入量进行转子系统配平计算[9]。但文献[10]研究表明，对于航空发动机等复杂转子机械，转子基频振动并不只是由不平衡引起，也会受到其他因素影响，尤其是当系统中存在同频激振转子时。文献[3]、[11]研究指出，转子基频振动测量值主要由不平衡振动、同频干扰振动、测量误差、随机误差几部分组成。其中，同频干扰振动主要由同一基座上的驱动转子传递而来。此时，若直接使用转子基频振动作为系统安全状态监测或动平衡计算的特征参数，势必会造成监测系统出现虚警或漏警，导致动平衡效果大打折扣。

为研究同频干扰振动对转子系统不平衡振动测量的影响，本文在动平衡试验中复现了这一现象，发现同频干扰振动会使特定方向测量的基频振动严重偏离不平衡振动响应。为保证不平衡测量的精确性，确保动平衡效果，建立了一种基于双向测量的转子真实不平衡响应分析技术，可通过不同配重构型试验中转子系统同一截面不同方向的振动测量值分析出转子系统的真实不平衡量。

2 不平衡试验测试分析

2.1 不平衡测试系统搭建

不平衡测量及动平衡试验在图1所示的地面转子实验台上进行。实验台转子系统由驱动电机、联轴器、带单级风扇盘及叶片的转子组件(模拟压气机结构)组成。其中，转子组件由前、后轴承支撑，通过联轴器与驱动电机连接，驱动电机与支撑轴承固定在试验器基座上。通过在风扇盘沿周向均布的36个配平孔内加装不同的配重，完成转子组件不平衡量的调整。不平衡测试系统由风扇端轴承座上加装的三向振动传感器、转速传感器、转速信号调理器、高速同步采集器等组成，如图2所示。

图1 地面转子实验台Fig.1 Ground rotor tester

图2 不平衡测试系统Fig.2 Unbalanced test system

测量的基本原理为高速同步测量转子系统的振动信号及转速信号(带基准键相)，通过数字信号处理技术获取基频振动幅值及相位。图3为测试系统原理图。

图3 转子不平衡测试系统原理图Fig.3 Schematic diagram of rotor unbalance testing system

2.2 测试数据分析

在转子系统无配重构型(初始)下进行转速台阶试验，依次在不同转速点稳定运行，录取振动及转速数据，确定系统动力学特性。图4 给出了获取的风扇水平方向(y向)与垂直方向(z向)振动时域数据。由图可知，y向最大振动峰-峰值接近12g，z向最大振动峰-峰值仅3g左右，据此判断转子y向支撑刚性远小于z向的[12-13]，这与其轴承座通过垂直方向的悬臂固定在底座上的结构特性相符。图5 示出了风扇y向与z向的振动时频分析结果。可见，转子系统的振动主要来自于与转速相关的高阶振动，基频振动只占一小部分，表明转子不平衡并不是该系统的主要激振源。

图4 转子系统振动时域数据Fig.4 Time domain data of rotor system vibration

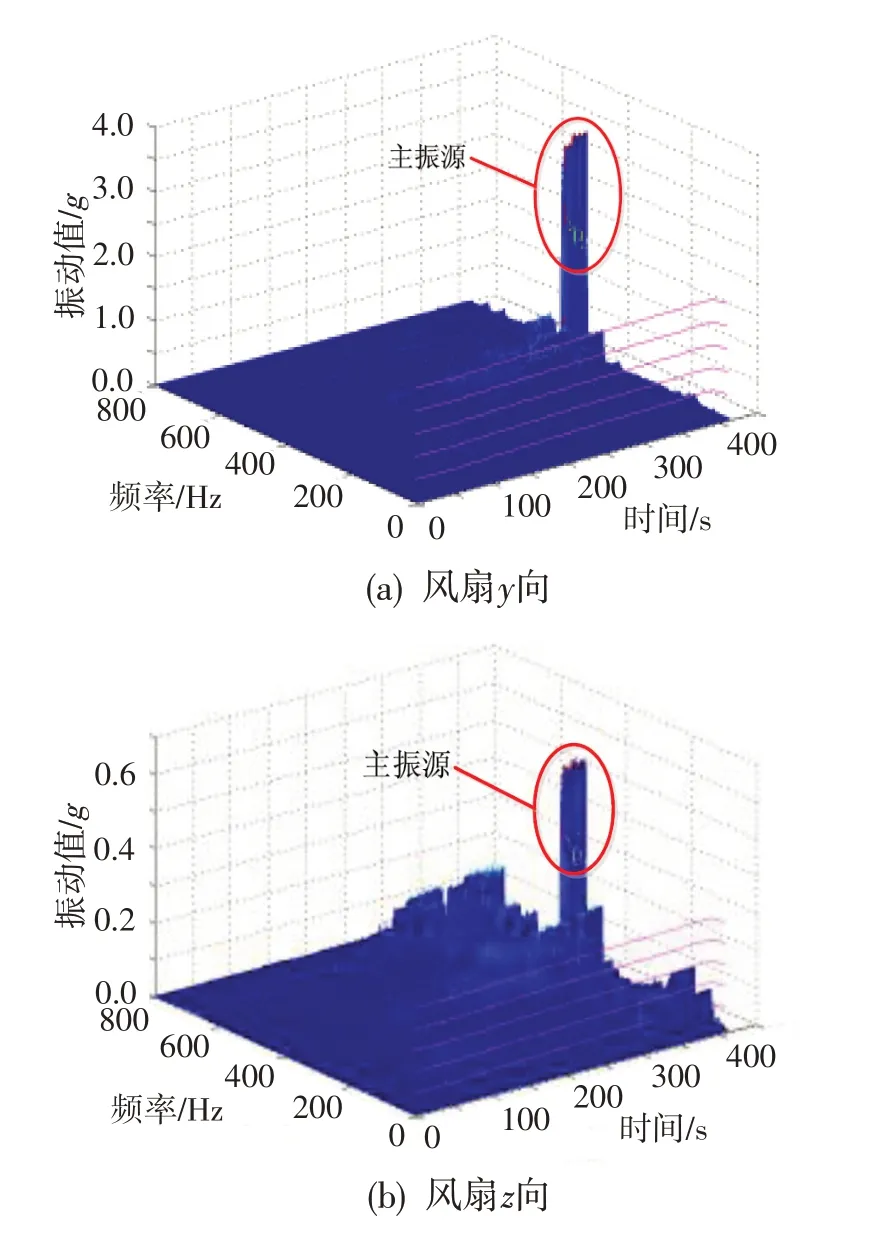
图5 转子系统振动时频分析图Fig.5 Time domain analysis chart of rotor system vibration

提取转子基频振动数据进行动平衡分析。在加装不同量级配重后，风扇z向基频振动幅值的减小幅度始终较小，最大只降低30.9%；而y向在同配重构型下可降低77.3%。此外，风扇y向与z向支撑刚度存在较大差异的情况下，初始构型风扇y向与z向的基频振动幅值并无太大差异。图6、图7分别为不同配重构型下风扇y向与z向传感器测取的基频振动幅频和相频曲线。由图可知，y向基频振动幅值随转速变化的规律基本符合不平衡载荷随转速变化的规律，且在较低质量配重构型下(残余不平衡量较大，相位测量较为准确)基频振动相位随转速基本稳定，表明风扇y向基频振动基本只受不平衡响应影响[14-15]；z向基频振动幅值随转速变化的规律与不平衡载荷随转速变化的规律出现了明显偏离，基频振动相位在较低质量配重构型下也出现了较大的变化。据此，综合分析认为风扇z向基频振动很可能受到了转子不平衡外的其他因素影响。

图6 风扇y向与z向转子基频振动幅频对比Fig.6 Amplitude comparison of rotor fundamental frequency vibration of ydirection of fan and zdirection of fan

图7 风扇y向与z向转子基频振动相频对比Fig.7 Phase comparison of rotor fundamental frequency vibration of ydirection of fan and zdirection of fan

3 真实不平衡量分析方法的建立

转子机械振动通常可表示为多个正余弦函数相叠加的形式。对于不平衡振动，根据其线性假设原理可将其时域波形用单个正余弦函数B×sin(ωx+α)的形式表示[16]，若同时存在其他振源传入的同频干扰振动C×sin(ωx+β)，则所测得的基频振动如式(1)所示，即测量获取的基频振动与真实的不平衡振动的频率相同但幅值、相位不同。这与试验中风扇z向基频振动的试验测量结果一致。

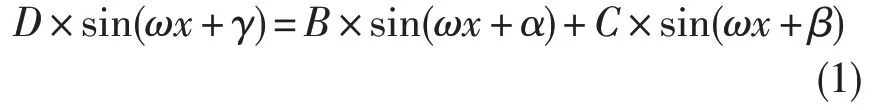
式中：D、B、C为振动幅值，ω为转子旋转频率，α、β、γ为不平衡相位信息。

为分析同频干扰振动对动平衡过程的影响，假设初始试验测量获取的基频振动为V0，真实的不平衡振动为V0′；加配重后测量获取的基频振动为V1，真实的不平衡振动为V1′；影响系数为A；配重为W。因动平衡过程只改变了转子不平衡构型，故可认为其他振源产生的同频干扰振动保持不变(相同转速与测点情况下)，设为V′(V′变量均为包含幅值与相位的复数变量)，则：

影响系数动平衡法中的影响系数可采用下式计算：

配重可采用下式计算：

综上可知，同频干扰振动不会影响影响系数的计算，但会影响动平衡方案的计算，导致计算的配重与实际所需的配重出现偏差，影响动平衡效果。此外，还会导致无法准确测量转子的真实不平衡响应，影响评估效果。

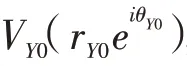
当风扇y向与z向测量的真实不平衡相位基于同一基准点且已消除不同测量通道引入的相位误差时，相同配重构型及转速下不平衡相位大小应相等，即：

方程组(5)、(6)中的未知项有VZ0′、VZ1′与VZ′(复数)共6个未知变量，同时也可被分解为6个实数方程，因此可直接求解出所有未知项。若两个方向的基频振动都不等于不平衡振动，可根据相同的方法建立方程组，但需建立包含4 种配重构型下试验数据的20个方程(包含20个未知变量)。

4 方法验证

为验证提出的基于双向测量的转子真实不平衡量响应分析技术的有效性，分别利用2.2节中初始试验与19.41g∠202°、12.95g∠197°及11.49g∠203°配重构型下的3组试验，以3 000 r/min转速点数据为例，计算出3 组试验对应的初始构型下风扇z向的真实不平衡振动VZ0′及同频干扰振动VZ′，相关数据见表1。

表1 动平衡试验数据Table 1 Dynamic balance test data

分别利用方程组(5)、(6)求解出3 组试验对应的初始的风扇z向真实不平衡振动VZ0′及同频干扰振动VZ′，结果见表2。由表可知，对于所计算的3组初始的风扇z向真实不平衡振动，相对于均值幅值最大偏差10.84%；对于同频干扰振动，相对于均值幅值最大偏差5.19%，相位最大偏差5.04%。以上结果表明了这一分析技术的工程有效性。