问题链：“趣动数学”课堂之思维支点

茅雅琳

摘 要：“趣动数学”课堂，教师要善于根据“学生已有的知识方法、现有的思维水平和本课的学习目标”设计问题链，以激发学生的思维活动，习得新知，提升技能。本文以“角”的教学为例，分别从前置思考、设计呈现以及后续追问三个角度，对问题链的设计进行了阐述和探讨。

关键词：问题链;“趣动数学”课堂;思维活动

我们倡导的“趣动数学”课堂，不是简单地让学生记住一些概念公式，学会一些解题技巧，掌握一些学习方法，而是为兴趣而教，为思维而教，为核心素养的培养而教。数学教师要善于借助问题链的设计，激发学生的思维活动，让学生习得新知，提升技能。这里的问题链，首先可以理解为问题串，是教师根据教学内容和学生思维水平而设置的一系列问题;其次，它们并不是简单的孤立问题的堆砌，而是层层递进，由浅入深，环环相扣，呈螺旋式上升;最后，它们的产生，既立足于课前预设，又源自课堂生成，既有具体的问题，又有模糊的问题框架。下面笔者结合人教版七年级上册“角”第一课时的教学实践，对“趣动数学”课堂的问题链设计进行思考，期待各位同仁批评指正。

一、问题链设计的前置思考

“趣动数学”课堂可以看成是由问题链串联而成的，整个课堂就是一个不断地提出问题、解决问题的场所。由此，问题链的设计显得至关重要，它直接决定着课堂的核心，把控着课堂的方向，决定着课堂的效率。基于问题链在课堂中的决定性地位，教师在设计问题链之前必须思考以下三个问题。

1.学生已有的知识、方法——决定问题的梯度

按照建构主义理论，学习者已有的生活经验、学习方法和知识积累，决定着他们解决问题的思路和方式。教学，并不是简单的知识和方法的“灌輸”，而是以已有的知识和方法作为学习的生长点，引导学生在已有学习经验的基础上，生长出新的知识经验。学生在小学二年级时就学过角，他们认识生活中的角，并会指出角的顶点和边。再学习角，除了认识生活中的角以外，还需要从静态、动态两种角度理解角的定义，并会用正确的方法表示角。这里的再学习，体现了知识的螺旋式上升。从另一个角度来看，刚学习了线段的两种表示方法，这里角的表示方法将与线段的两种表示方法进行类比，扩充为四种，还体现了方法的螺旋式上升。针对以上分析，教师的问题应该层层递进，富有梯度，问题链必须体现递进性。

2.学生现有的思维水平——决定问题的难度

数学是思维的体操，而问题则是思维的媒介。学生现有的思维水平，制约着他们解决问题的速度和质量。对七年级的学生而言，虽然小学已经对角有过初步的了解，但是没有进行系统的研究，他们的读图识图能力比较薄弱，对于几何图形的认识还停留在基本的概念之上，教师的问题应该紧紧围绕概念，由易到难，直至揭示概念的本质。

3.学生本课的学习目标——决定问题的广度

问题链的设计，不在于量的多少，而在于激发了学生哪些层次的思维。教师要对学生学习目标有个准确清晰的定位，“角”第一课时的学习目标有以下几点：（1）会从两种不同角度理解角的定义;（2）会用不同的方法表示同一个角;（3）会根据定义寻找一个角，并且会区分不同的角。教师的问题应该紧紧围绕学习目标，有的放矢，指向明确精准，问题链更需具有导向性。

总之，教师必须坚持学生立场，重视已有经验，设置具有递进性、贴合性和导向性的问题链，发展学生的数学思维。

二、问题链设计的教学实施

1.“角的定义”问题链设计

朱永新教授指出，理想课堂需要学生的生命参与。只有建立在学生已有知识基础上的问题链，才能提高学生的课堂参与程度。所以，我们的第一个总问题是：同学们学过角，请你们说说怎样的图形称为角？对于这个问题，所有学生都可以回答，回答的角度却不尽相同。教师通过预设学生答案，设计如下问题链。

生：由一个顶点、两条边组成的图形叫作角。

师：什么是顶点？什么是边？

生：由两条射线组成的图形叫作角。

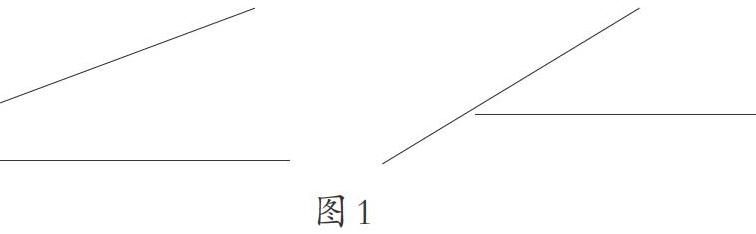
师：如图1，能称为角吗？

生：有公共端点的两条射线组成的图形叫作角。

师：你们所说的顶点和边是什么呢？

（学生达成共识：有公共端点的两条射线组成的图形叫作角，其中这个公共端点称为角的顶点，两条射线称为角的两条边）

师：刚才是从静态的角度认识了角，我们能否从运动的角度来认识角呢？请同学们仔细观察打开圆规的过程，你们有什么发现？

生：一条射线绕着它的端点旋转而形成的图形称为角。

师：你能从运动的角度来认识小学时学过的平角和周角吗？

生：射线绕着端点旋转，当终止位置与起始位置成一条直线时，得到平角。继续旋转，当两者重合时，得到周角。

思考：虽然学生在小学时就学过角，但他们只是初步认识角的形状，而用严谨的数学语言来描述角还存在一定问题。这里问题链设计主要采用追问的形式，通过系列追问，激发学生不断思考，实现由模糊到清晰、由静态到动态、由大致到精准的转变，从而让学生深刻理解角的定义。

2.“角的表示方法”问题链设计

问题链的设置，应该基于学生的思维水平和已有经验，暴露学生迫切需要解决的问题。学生根据前期的学习经验，会进行角的表示方法的迁移。基于以上对学生的了解，我们的总问题是：前面我们研究过线段的表示方法，那么怎样表示一个角呢？预设学生的答案有如下三种：（1）用两个大写字母表示;（2）角的表示方法应该和直线、射线、线段不同，这里的两条射线和端点都应该体现出来;（3）用三个大写字母表示，表示成角OAB。教学中，我们可以设计如下问题链。

师：数学追求简洁，我们可以用符号“∠”来表示角，角的顶点是两条边的公共端点，通常写在中间，可以写成∠AOB。

师：表示角还有其他方法吗？

生：是否可以像表示线段那样，用一个小写字母表示？

师：可以用一个字母表示成∠O，其中的O表示一个点，写成大写字母。

生：能用小写字母表示角吗？

师：若用一个小写字母表示角，我们通常在角的顶点处画上一段弧，标上希腊字母α，这个角还可以表示为∠α。或者标上数字1，这个角也可以表示成∠1。

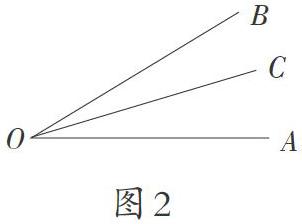
师：请用不同的方法表示出图2中的角。

生：老师，您让我们表示哪个角？

師：当一个顶点处有多个角时，确实有必要表示清楚，请表示图2中最大的角。

生：有四种表示方法，分别是∠AOB，∠O，∠α，∠1。

生：不对，只有一种表示方法，是∠AOB。如果表示成∠O，无法确定表示的一定是最大的角;如果表示成∠α或∠1，则无法在图形上进行标注，也缺乏直观性。

师：我们研究角的表示方法，将图形用符号语言表示，应该指向明确，直观可视。图2中最大的角最恰当的表示方法就是∠AOB。

学生达成共识：虽然角的表示方法共有四种，但是当一个顶点处有多个角时，我们要选择恰当的方法来表示。表示一个角时我们要遵循的原则是唯一性和直观性。

思考：类比学习知识，并非简单直接的“套用”，而是需要根据新学的内容进行必要的调整和修订。角的表示与线段的表示不尽相同，这里的问题链设计采用激疑的形式，不断让学生发现问题、提出问题和解决问题。

3.“数角的个数”问题链设计

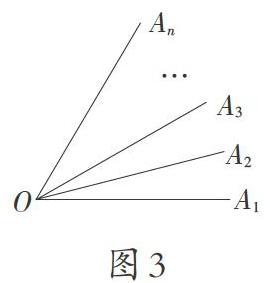
为了让学生理解角的定义，教师提出第三个总问题：图3中共有几个角？

作为一种教学理念，因材施教一直被人们奉为教学的最高层次。我们的数学课堂也要因“班”施教，因学设问。在教学过程中，教师根据所教班级学生的思维水平和能力现状，可以设计以下两种不同的问题链。

第一种：由特殊到一般，进行方法探寻和规律梳理（适用于思维能力较弱的班级）。

师：如图4，分别有几个角？

生：分别有1个角、3个角、6个角。

师：你是怎么得到6个角的？

生：分类数角，单个的角共有3个，2个组合的角共有2个，3个组合的角有1个，所以一共有6个角。

师：图5中共有几个角？

生：[n（n-1）2]个角。

师：请说明理由。

生：用刚才的方法分类数角，角的个数是1+2+…+n-1，求和得[n（n-1）2]。

师：能否从角的定义入手？每个角可以看成由两条射线组成，如果其中的一条射线确定，那么哪些射线能和它构成角吗？

生：以OA1为角的一条边，这样的角有n-1个;以OA2为角的一条边，这样的角有n-2个;以此类推，图中角的个数是1+2+…+n-1。

师：还有其他数角的方法吗？

生：若以OA1为角的一条边，这样的角有n-1个;若以OA2为角的一条边，这样的角也有n-1个;这样共有n个n-1，其中每个角都重复算了一次，所以角的个数是[n（n-1）2]。

师：我们之前学过的线段条数、三角形个数、球赛次数、握手次数和送贺卡张数等，数的方法都是一样的，我们要善于把学过的方法进行归纳、总结。

第二种：由一般到拓展，注重方法提炼和结论推广（适用于思维能力较强的班级）。

师：图5中共有多少个角？

生：[n（n-1）2]个角。

师：请用两种方法说明理由。

师：我们遇到过类似问题吗？

生：遇到过，如线段条数、三角形个数、应用题中的球赛比赛场次、握手的次数等。

师：这些问题的共同特征是什么？我们解决的“通法”是什么？

……

思考：针对思维能力不同的班级，问题的呈现顺序不同。对能力弱的班级，从解决特殊问题入手，归纳出解决一般问题的方法，学生逐渐突破，缓慢提升，循序渐进。对能力强的班级，教师则直接抛出一般性问题，不断地质疑追问，让学生对自己的解题思路和方法进行反思和总结。两种不同的问题链设计，最终的指向是相同的。

三、问题链设计的后续追问

其实，教师的课堂驾驭能力不同、教学风格不同，设计出的问题链不尽相同。再者，问题链的设置，既有课前的预设，也有课堂进程中的生成，学生的答案也会决定问题链的走向。另外，上述设计过程只是概念课问题链设计的一种展示，对于习题课和复习课，我们该怎样设计问题链呢？我们是否可以探寻不同课型的问题链设计的基本范式？推而广之，不同学科的问题链又该怎样设计呢？这些都值得在后续的研究中继续思考和探索。

鲍波尔说：“正是问题激发我们去学习，去实践，去观察。”我们愿以问题链设计为原点，激发“趣动数学”课堂的内在动力，让每个学生在数学课堂中学会思维，获得成长。

（作者单位：江苏省南通市海门区东洲国际学校）

参考文献

[1]章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报，2013（6）：5-8.

[2]郭思乐.教育走向生本[M].北京：人民教育出版社，2001.