黄河口盐沼湿地植被群落适宜生境模拟Ⅰ：理论

易雨君，谢泓毅，宋 劼，杨志峰，4

（1.北京师范大学教育部水沙科学重点实验室，北京 100875；2.北京师范大学水环境模拟国家重点实验室，北京 100875；3.交通运输部规划研究院环境资源所，北京 100028；4.广东工业大学环境生态工程研究院，广东广州 510006）

1 研究背景

盐沼植被适宜生境保护是维持黄河三角洲生物多样性的重要环节之一［1-2］。许多研究表明，盐沼植被的演替与盐沼的海拔高度和水文过程有关，尤其与地下水过程关系紧密［3］。不同地下水流动模式下，非生物因子梯度，如土壤盐度与含水率梯度在空间上存在明显差异，这种差异直接导致了盐沼植被适宜生境的变化［4］。对于盐沼植被适宜生境的模拟始于偏好曲线法，该方法基于生物对生境因子的偏好，构建环境因子与生物偏好之间的关系，得到物种生境的适宜程度［5］。但该方法没有考虑环境因子之间的相互作用，不能适用于环境因子相互作用关系复杂的情况。

为了解决偏好曲线法的局限，一些研究开始采用多元统计方法，通过建立目标物种分布与环境因子之间的统计关系来模拟适宜生境，包括多元线性回归法、岭回归法、主成分回归法、逻辑回归法、广义线性模型和广义可加模型等［6-7］。偏好曲线法和多元统计方法能较好地描述物种对多环境因子的响应问题，并和水动力水质模型相结合，得到适宜生境范围的时空演变过程。但上述方法主要基于环境因子和生物选择的统计关系［8］，无法考虑生物的动力过程。有研究提出了基于生物生长动力过程的适宜生境模拟方法［9］，该方法能够模拟环境因子和生物过程以及两者之间的动态作用关系［10］。目前基于生物生长动力过程的适宜生境模型主要有元胞自动机法（Cellular Automata，CA），该方法能模拟物种的生长和扩散过程［11］；同时，有研究从生态学角度出发，提出了模拟种群增长和种间竞争的模型［12］。然而，模拟种群扩散和增长的元胞自动机模型，和模拟种间竞争的模型，往往基于静态的环境因子空间分布，或将空间视为均质统一体，无法体现环境因子以及生物分布在空间和时间上的异质性。因此，针对目前生境模拟中面临的环境因子时空异质性与生物生长、扩散以及种间竞争之间无法兼顾这一问题，需提出新的生境适宜度模拟方法。

盐沼湿地地下水埋深较浅，地下水过程对盐沼植被根系所在的浅层土壤影响显著而迅速，地下水过程时空变化特征对盐沼植被生境适宜度的分布状况会有显著影响［13］。目前已有一些研究表明地下水动力三维数值模拟应用广泛，对于滨海盐沼湿地地下水模拟也较为适用［14］。

本文基于MODFLOW 模型构建潮汐和径流共同作用下地下水动力模型，并构建土壤盐度模型模拟盐度的时空变化；将元胞自动机模型和改进的Logistic模型耦合，构建综合考虑盐沼植被生长、扩散及种间竞争的盐沼植被种群增长-竞争动力学模型，其中，元胞自动机模型模拟植被的空间扩散，改进的Logistic 模型模拟盐沼植被的生物量积累。将地下水动力模型、土壤盐度模型与植被种群增长-竞争动力学模型相结合，模拟不同径流过程和潮汐共同作用下，盐沼植被群落的适宜生境及生物量的时空分布。

2 研究区及监测实验设计

2.1 研究区及监测样点布设黄河三角洲国家级自然保护区位于现行黄河流路和黄河故道的入海口处，总面积达到15.3×104hm2，分为实验区、过渡区和核心区。黄河自西向东穿过研究区，最终汇入渤海，是研究区最主要的淡水源，也是区域地下水的主要补给源。浅层地下水的埋深非常浅，约为0～3 m，以微咸水、咸水和卤水为主。地下水位较高，一般在-2.5～7.5 m。自海向陆环境梯度上，日本鳗草-互花米草-翅碱蓬-柽柳-芦苇等盐沼植被呈典型带状分布。

在黄河口自然保护区内，植被具有典型带状分布格局，依据盐沼植被分布分成5个区，依次为裸滩区（W1）、翅碱蓬区（W3）、交错区（W5）、柽柳区（W7）和芦苇区（W10），如图1所示。选取受人为干扰较小的区域，设置长约为4 km的样带，沿样带设置5个监测样点。2019年3—10月定期（每月25日）监测植被生长状态、土壤及地下水数据，并采集表层土壤样品进行理化性质分析，于2019年7月2—29日黄河调水调沙期间开展了为期28 d的持续原位监测，每个监测点设置两个不同开筛深度的地下水监测井，井深3 m，开筛深度分别为0.5～1 m 和2～2.5 m（图1（c））。同步监测土壤盐度、含水率、地下水埋深、黄河水位和渤海潮高等指标，持续监测时长约700 h。

2.2 原位监测实验于2019年7月2—29日期间，每隔3日采集1次浅层土壤（0～40 cm）样品，并测定其盐度和含水率。每个监测点取3个平行样，以平行样均值作为测定值。浅层土壤含水率采用烘干称重法测定，盐度采用土壤浸出液法［15］测定。

浅层土壤盐度和含水率的监测结果（图2）表明，裸滩区、翅碱蓬区和交错区（W1、W3、W5）浅层土壤盐度和含水率较为接近，与柽柳区（W7）相比，上述区域浅层土壤盐度均明显偏低，而含水率均明显偏高。由海向陆至黄河梯度上，浅层土壤盐度和含水率的变化范围增大。近海的翅碱蓬区土壤盐度较低而含水率较高，变化范围均较小；与之相反，靠近黄河的柽柳区土壤盐度较高，含水率较低，变化范围均较大。位于两者之间的交错区与翅碱蓬区的盐度和含水率较为一致，但变化范围显著变大。交错区作为过渡区，其含水率和盐度为翅碱蓬适宜范围，又因含水率和盐度的变化范围大，为柽柳提供了适宜生境［16］。芦苇区（W10）盐度明显偏低，含水率的均值和变化范围最大。

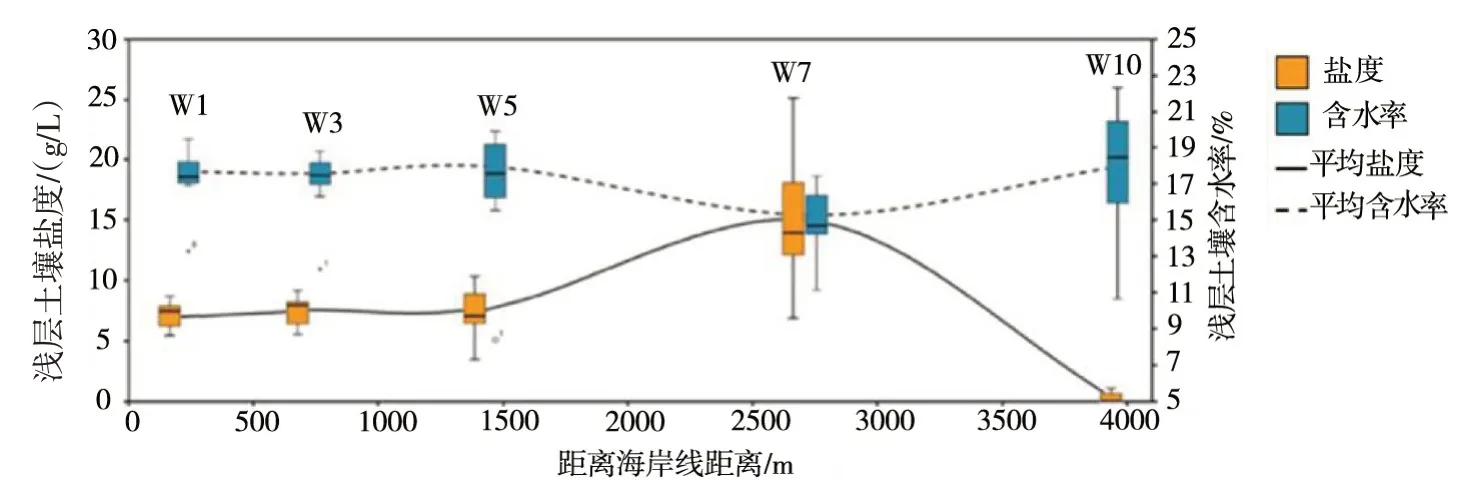
图2 浅层土壤含水率和盐度的监测结果

开展原位监测实验的同时，在潮滩上和黄河岸边分别设定了潮位和黄河水位监测点，使用水位记录仪分别记录实时潮高和黄河水位。潮汐和黄河水位的监测结果（见图3）表明，样带北侧存在大小潮持续影响，潮汐周期约为14 d，大潮出现在7月6日和18日前后，小潮出现在7月12日和26日前后；样带南侧黄河水位受到人为扰动较大，水位波动剧烈。在调水调沙前（7月2—9日）、中（7月10—16日）和后期（7月17—29日）变化显著，调水调沙中期黄河水位激增，水位波动较大，调水调沙前期和后期水位较低。

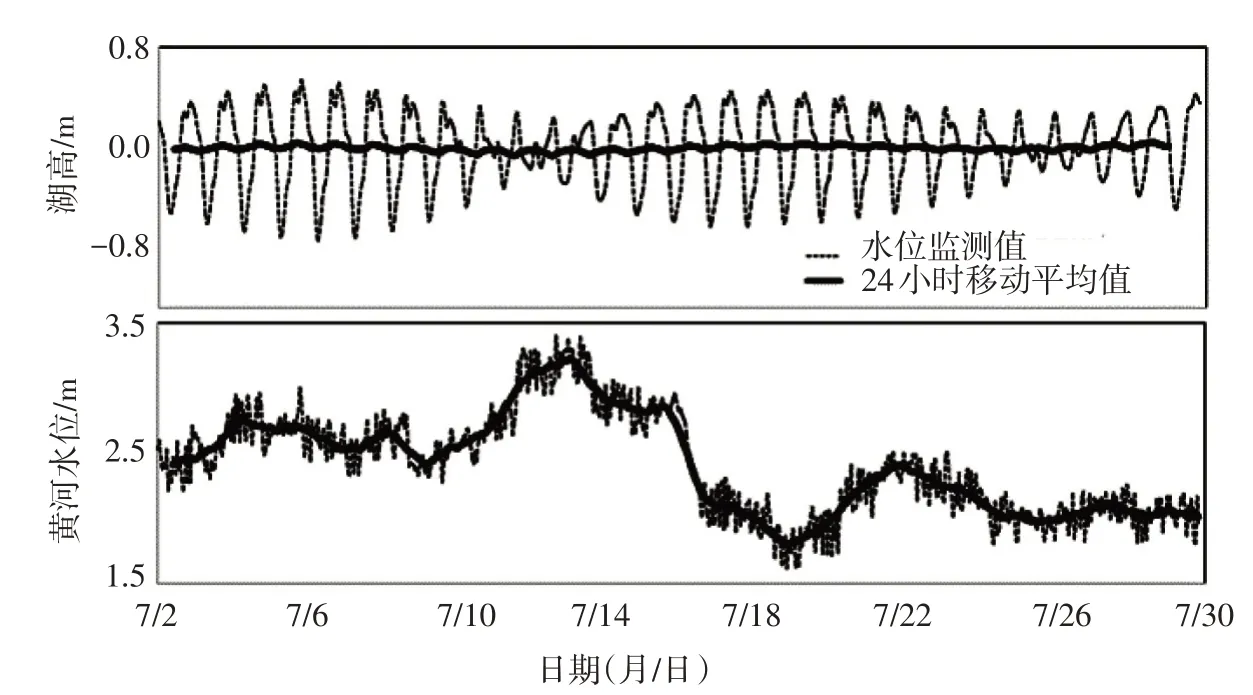
图3 潮高和黄河水位变化监测结果

3 模型构建

3.1 地下水动力模型采用MODFLOW模型模拟地下水动力条件。基于达西定律和渗流连续方程和实际水文地质条件，建立浅层地下水三维非稳定流数学模型［17］，公式如下：

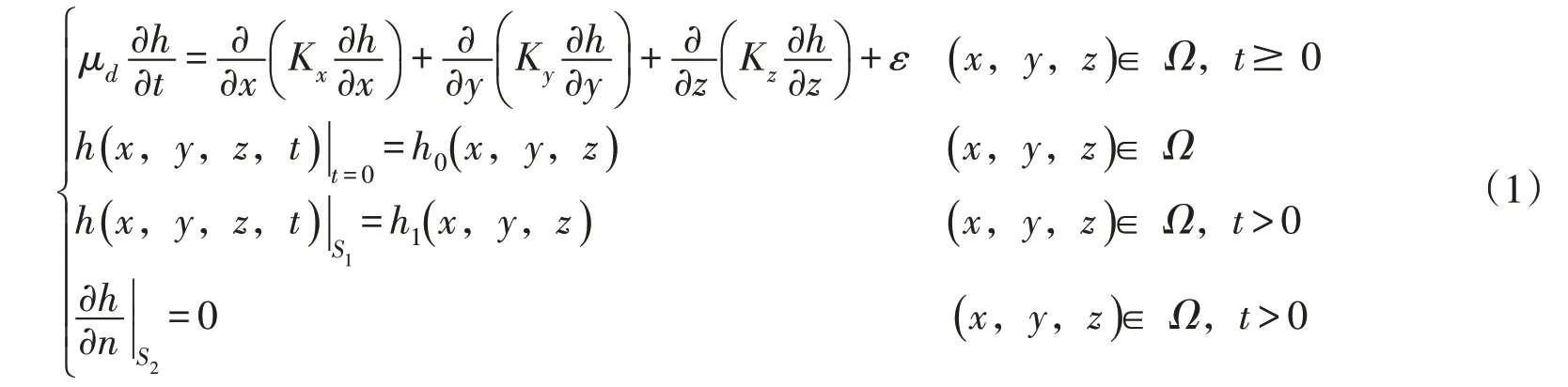
式中：Ω为渗流模拟区域；h为含水层水头，m；Kx、Ky、Kz分别为x、y、z轴的渗透系数，m/d；μd为给水度，1/m；ε为源汇项，1/d；h0为初始水头，m；h1为第一类边界的水头，m；t为时间，d；S1和S2代表第一类和第二类边界。

数学模型的求解采用有限差分法，强隐式迭代法解算器（Strongly Implicit Procedure，SIP）求解，最大迭代次数为50，收敛的判别标准和残差判别标准为0.001，网格考虑干湿转换。

3.2 土壤盐度模型基于原位监测数据，通过冗余分析（Redundancy Analysis，RDA）研究地下水相关指标、多种环境因子与土壤含水率、土壤盐度间的关系。由于解释变量和环境变量的单位均不同，在进行RDA分析前，采用Z分数（Z-Score）标准化方法对所有变量进行标准化，其公式为：

式中：x为个案值；μ为总体平均值；σ为总体的标准偏差。

基于瞬时值的浅层土壤含水率（SM）和盐度（SS）与环境因子的RDA 分析结果见图4。前2 个排序轴特征值总和为98.14%，表明环境因子对浅层土壤含水率和盐度均有较好的解释。图4显示地表高程和潮高与浅层土壤盐度显著正相关，其他环境因子影响较小。其原因可能为高程越高，地表裸露时间越长，土壤中水分蒸发，而盐分滞留在土壤中导致。然而，地下水盐度与浅层土壤盐度相关关系较弱，表明土壤盐分变化受到地下水盐度变化影响较小，土壤盐分的变化是一个累积过程，与地下水盐度瞬时值关系较弱。

采用广义可加模型（Generalized Additive Models，GAMs）量化土壤盐度与环境因子之间的关系。本研究中光滑函数使用薄板样条函数，以约束性最大似然法作为光滑参数估计方法，模型拟合度检验使用残差偏差法。

GAMs 模型的响应变量为土壤含盐度（SS），解释变量为含水率（SM）、潮位（TIDE）、潮差（TIDEH）、地下水埋深（GWD）、地下水盐度（GWS）、地表高程（ELE）、距离黄河河岸的距离（DIS）和黄河水位（YRWL）。采用Pearson相关系数法来检查环境因子之间的共线性，发现ELE与DIS、SM与GWD、TIDE与TIDEH、DIS与GWS存在显著相关关系（见图5），在模型中只保留其中一个变量，因此本研究选取ELE、GWD和TIDE。

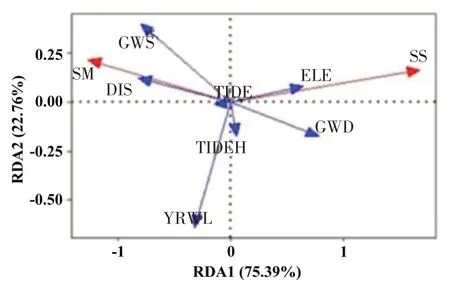
图4 浅层土壤含水率和盐度与环境因子RDA分析结果

图5 环境变量的Pearson相关系数检验结果

通过单变量检验和交互因子检验设置光滑函数以及参数，GWD、GWS和ELE通过单变量显著性检验，可以单独作为模型的解释变量，模型的解释率在3.31%～50.90%。以GWD、GWS和ELE为模型参数基础，考虑它们之间交互因子的影响，建立多个GAMs方程。3个因子之间的交互项均对解释变量有显著影响，模型解释率在51.80%～68.10%，环境因子之间的交互作用对SS有显著的影响。

以上述单、双因子的GAMs模型为基础，采用向前逐步回归法对模型进行优化。按照环境因子影响的显著程度调整模型结构，共建立10个含盐度模拟GAMs模型（见表1）。以解释率残差偏差评价模型拟合度，解释率越高残差偏差越小，则模型拟合程度越好。为避免模型过度拟合，采用似然比检验判断是否显著提高模型性能，使用复杂模型和简单模型的比例应该近似卡方分布，故以P值进行判断［18］。由表1可知，Model7的解释率最高（69.50%）、残差偏差最小（178.50），是最优模型，模型结构为：

式中：s为单因素函数；te为交互作用函数。

最优模型的SS计算值与监测值拟合结果见图6（a），决定系数R2=0.6959，表明模型预测值与监测值间拟合度较高。利用2019年4、5和6月实测数据（n=12）进行模型验证（见图6（b）），预测值和实测值的R2为0.6505，模型可用于预测。

表1 土壤盐度GAMs模型结构优化

图6 最优模型（Model7）的浅层土壤盐度率定和验证结果

3.3 植被种群增长-竞争动力学模型基于研究区典型盐沼植被（翅碱蓬、柽柳和芦苇）对地下水埋深和浅层土壤盐度耐受性的实验结果，将研究区剖分成1223×1038个30 m×30 m的正方形网格，耦合元胞自动机和改进的Logistic函数，建立研究区典型盐沼植被种群增长-竞争动力学模型。

3.3.1 基于元胞自动机的种群扩散模块 在自然条件下，盐沼植被的种子的发芽率以及幼苗的定植率较低，地下茎的克隆繁殖是其主要的定植和繁殖扩散方式。盐沼植被地下茎的克隆扩散过程受到植株状态和环境因素的共同影响，其中土壤水、盐指标是影响地下茎克隆扩散过程最为关键的因子。因此，本研究选用地下水埋深和浅层土壤盐度作为根茎出芽率的函数。采用元胞自动机方法模拟［19］，传递规则为：（1）当地下水埋深和浅层土壤盐度处在盐沼植被可生长的范围时，盐沼植被继续存活，并具有一定的生长力；（2）当地下水埋深和浅层土壤盐度处在盐沼植被最适宜生长的范围时，盐沼植被生长处于旺盛的状态；（3）当地下水埋深和浅层土壤含盐度处在盐沼植被不可生长的范围时，盐沼植被在下一时刻死亡；（4）当元胞没有存活的盐沼植被且地下水埋深和土壤含盐度处于盐沼植被可生长的范围时，下一时刻该元胞内有可能产生新的盐沼植被，其概率P为：

式中：i为邻域元胞编号；Ni为邻域元胞的出芽数；r为元胞的出苗率。

在每一个元胞内计算3种盐沼植被的生境适宜度。假设该元胞内的淹水深度和土壤盐度两个状态中，存在任何一个状态不适宜盐沼植被生长，则盐沼植被的生境不适宜，其计算公式为：

式中：SI为一种盐沼植被的生境适宜度，其取值为0 或1，当取值为1 时表明该元胞内植被可以生长，取值为0时说明该元胞内植被不可生长；SID为地下水埋深胁迫量，取1时表示该元胞内该盐沼植被不受地下水埋深胁迫，取0 时表示该元胞内该盐沼植被处于受地下水埋深胁迫无法正常生长；SIS为土壤盐度胁迫量，取1时表示该元胞内该盐沼植被不受土壤盐度胁迫，取0时表示该元胞内该盐沼植被受土壤盐度胁迫而无法正常生长。

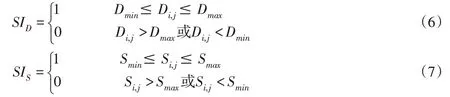
式中：Di,j为该元胞的土壤含水率；Si,j为该元胞的土壤盐度值，g/L；Dmax和Dmin分别为地下水埋深的阈值；Smax和Smin分别为土壤盐度的阈值。

3.3.2 基于改进Logistic函数的植被生长-竞争模块 Logistic生长曲线适用于处于无环境干扰下的植物萌发后正常生长过程的模拟，其形状为“S”形，分为发生、发展和成熟三个阶段，斜率先增大再减小。由于Logistic函数忽略了盐沼植被在不适宜环境下的生物量损失，因此本研究采用考虑生物量损失的Hill方程对Logistic函数进行修正［20］，同时引入盐沼植被的种间竞争函数［10］，提出考虑植物生物量损失和种间竞争的Logistic函数的数学表达式：

式中：Δt为模拟的时间步长，本研究关注于生长季内的变化，以月计；ΔRi为i月的盐沼植被生物量净增量，g/m2，本研究只考虑地上部分；ΔLi为i月的生物量增量，g/m2；ΔCi、ΔHi和ΔFi分别为i月因种间竞争、地下水埋深和土壤盐度导致的生物量损失量（干重），g/m2；ri为i月的内禀增长率；L为不适条件下的最大生物损失量，g/(m2·月)；Di为i月的地下水埋深，m；Dm为最适地下水埋深，m；Si为i月的土壤盐度，g/L；Sm为最适土壤盐度，g/L；p为模型形状参数，取值为2、4 或6［20］；h为半致死地下水埋深，m；s为半致死土壤盐度，g/L；βj,i-1为该盐沼植被的种间竞争系数；Rj,i-1为与盐沼植物竞争的另一种盐沼植物j在i-1月的生物量，g/m2。

3.4 模型耦合耦合模型的结构如图7所示。基于地下水动力模型得到地下水水位分布条件，通过GAMs方程计算得到土壤盐度分布条件，将土壤盐度和地下水埋深分布作为种群动力学模型的输入条件，利用元胞自动机模拟适宜生境的空间分布，在每个元胞内利用改进的Logistic函数计算盐沼植被的生物量。在此基础上假设，生长季开始时，盐沼植被在适宜生境处完成芽的扩散，在生长季内不会产生新的植株，只在芽分布处进行生长。运行植被种群增长-竞争动力学模型计算盐沼植被的适宜生境和生物量分布。

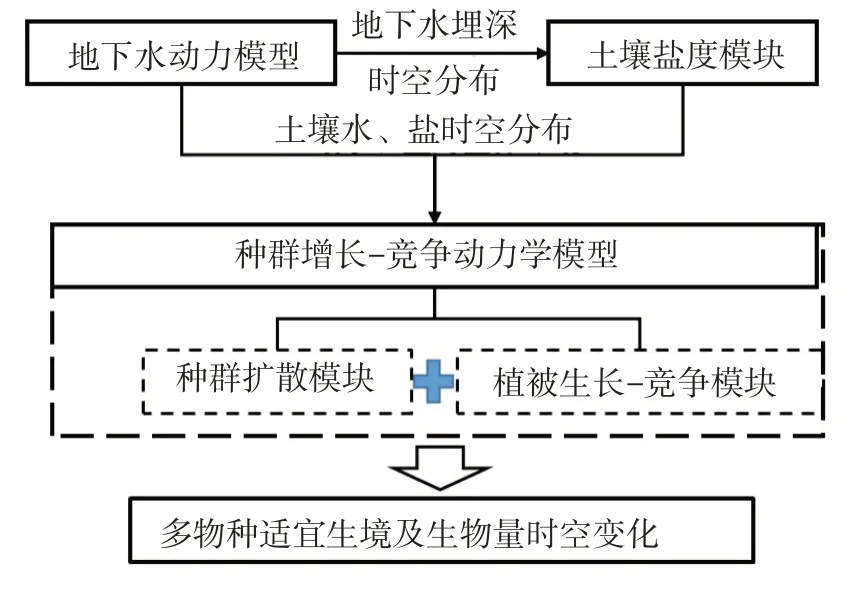
图7 模型结构图

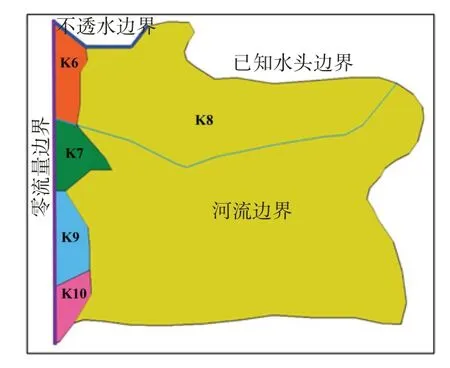
图8 模型边界及水文地质参数分区

4 模型率定与验证

4.1 地下水模型率定与验证黄河三角洲自然保护区模拟区面积约为46 km×46 km，其中陆地面积约为687 km2，处于河口咸淡水交互区，黄河和渤海对模拟区的地下水埋深有显著影响。将研究区划分为10 000个460 m×460 m的矩形网格，地下水监测井附近网格细化为230 m×230 m。根据全国重要地质钻孔数据库服务平台（http：//zkinfo.cgsi.cn/）提供的地质钻井图与土壤岩性信息，将研究区土壤浅层含水层概化为非均质、各向异性的潜水含水层（粉土黏土为主）和微承压含水层（砂土为主）两层，并通过空间插值的方法，将各含水层的顶板和底板概化，其中地表采用DEM卫星数据。模型的东北侧、东侧和南侧均为渤海，概化为已知水头边界；西北侧为堤坝，概化为不透水边界；西侧为自然的大陆地块，自西向东流量近似为零，概化为零流量边界；地表存在黄河径流，概化为河流边界。降水补给和潜水蒸散发在研究区内变化不大，渗透系数取值0.0167 m/d［21］。模型边界及水文地质参数分区见图8，参数取值参考文献［21］。

模型计算时段为2019年7月1—29日。使用4口地下水观测井的实测数据进行模型参数率定和验证，其中W1、W3和W7用于模型的参数率定，W5用于模型验证。模拟结果与实测数据的拟合度采用标准化残差（RMSE）进行评估，RMSE值越小拟合效果越好。模型调参后RMSE=7.79%，模型误差在合理范围内，模型的地下水位时间序列图（图9（a））中模拟值与实测值较为接近，证明模型率定完成。以地下水观测井W5实测数据进行模型的验证。模型验证中，RMSE=9.18%，模型的地下水位时间序列图（图9（b））中模拟值与实测值的较为接近，满足精度要求。

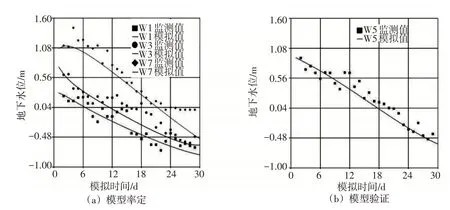
图9 模型率定和验证结果

4.2 植被种群增长-竞争动力学模型率定与验证在黄河三角洲地区关于芦苇、翅碱蓬和柽柳对地下水埋深和土壤盐度的耐受性，很多学者开展了室内移植实验、原位监测实验和模型模拟的研究。结合前人已有的研究成果和课题组的野外监测，确定了各物种出芽数和出苗率的取值见表3。考虑到目前相关研究中，对于地下水埋深胁迫和土壤盐度胁迫影响的协同影响的研究较少，本研究不区分出芽数和出苗率在地下水埋深胁迫和土壤盐度胁迫下的差异。

表2 3种典型盐沼植被的生境阈值

表3 不同生境条件下各物种出芽数和出苗率取值

Logistic函数中，3种盐沼植被的最大生物量的设置参照文献［4］的取值，芦苇为2437.24 g/m2，柽柳为3137.75 g/m2，翅碱蓬为5970.15 g/m2。模型的最适地下水埋深和最适盐度取上下限的均值，芦苇、柽柳和翅碱蓬的最适地下水埋深依次为-0.185、0.85和0.42 m，最适盐度依次为6.5、16和12.71 g/L。3个物种的内禀增长率取值参见表4。3种盐沼植被在生长季开始时的初始生物量构建的模型参数设为100 g/m2。

表4 内禀增长率参数取值

表5 种间竞争系数取值

图10 适宜生境模型模拟结果

3种盐沼植物的种间竞争系数参考文献［4］，在地下水埋深胁迫和土壤含盐度胁迫下取值见表5。模型模拟了不同土壤盐度下芦苇、柽柳和翅碱蓬的生物量，与已有监测结果的对比见图10，表明模型合理。

5 结论

在径流和潮汐的共同作用下，黄河口三角洲的水盐条件发生动态变化，进而导致盐沼植被群落呈明显的带状分布。为明确生境条件与植被群落间的影响关系，探究滨海盐沼湿地生态系统对自然和人类活动的响应规律。本研究基于野外观测数据建立了地下水水位、土壤水分和土壤盐度的地下水动力模型；将元胞自动机模型和改进的Logistic函数相耦合，构建了植被种群动力学生境模型，并将水动力模型与种群动力学生境模型相耦合，实现了包含土壤水盐协同作用和植被生长扩散作用两个过程的植被群落适宜生境及生物量的定量模拟和预测，突破了目前基于地下水动力学过程的适宜生境模型无法模拟植被生长扩散作用的局限。