基于深度阈值卷积模型的土石料级配智能检测方法研究

雷雨萌，陈祖煜，，于 沭，温彦锋，王玉杰，李炎隆

（1.西安理工大学省部共建西北旱区生态水利国家重点实验室，陕西西安 710048；2.中国水利水电科学研究院岩土工程研究所，北京 100048）

1 研究背景

土石料的级配性状直接影响到土石坝的力学特性与抗渗性能［1］。在坝体施工质量控制过程中，级配检测具有重要意义［2］。传统级配检测主要采用筛分法［3］，通过人工采样与筛分机筛分，计算得到级配数据，该过程较为耗时，难以满足机械化施工过程中快速、高效的需求。随着计算机科学的发展，图像识别作为一种新的检测手段，逐渐在众多领域中广泛应用，为土石料的级配检测方法研究提供了新的方向。

通过图像识别技术实现土石料级配检测，关键在于获取图像中颗粒的形状信息，并转换为级配数据。在目标物体形状提取与级配分析方面，国内外学者进行了大量研究。覃茜等［4］、王宇等［5］通过断层扫描技术，在CT图像的基础上实现了混凝土内部孔隙大小、形状的检测。涂新斌等［6］通过图像提取了土体颗粒的轮廓，并对不规则的颗粒形状进行了参数化描述。徐文杰等［7］基于数字图像技术分离了土石混合体中的块体，并通过块体轮廓建立了细观结构模型。Ding 等［8］通过二维切片图像重建了沥青混凝土的三维模型，论证了骨料在二维截面中的级配分布与三维状态下的真实级配分布之间的相似关系。Leonardo 等［9］基于阈值化与分水岭算法，实现了基于图像的沥青混凝土级配检测。Shilin 等［10］通过图像识别分析了筑坝材料的级配分布，并结合遗传算法与BP（Back Propagation）神经网络，建立了识别结果与真实级配分布之间的隐式关系，评估了图像识别的准确性。吕超等［11］通过扫描电镜获取砂土颗粒图像，在阈值化算法的基础上实现了毫米级以下的级配识别。于沭等［12］基于阈值化与边缘检测算法，建立了土石料级配快速检测系统，实现了工业级的级配快速检测。前述学者在图像识别方法上，均采用了基于阈值化的传统方法，该方法识别速度快但精度不足。随着人工智能的发展，图像识别技术取得了新的进展。Jonathan 等［13］提出全卷积神经网络（Fully Convolu⁃tional Networks，FCN），通过反卷积的方式使神经网络的数据分类能力从一维提升到二维，为深度学习在图像识别方向上的应用提供了思路。何凯明等［14］通过残差学习设计了深度残差网络（Deep Resid⁃ual Network，ResNet），极大提高了神经网络深度，并在此基础上提出Mask-RCNN（Mask Region Con⁃volutional Neural Network）图像识别模型［15］，为不同种类物体的识别与形状分析提供了基础。在级配检测及相关领域，基于深度学习的图像识别方法尚未有成熟应用，但同样为级配检测提供了新的理论依据与技术支持。

5 mm以下的颗粒含量对于土石料级配合理性具有重要意义，我国规范对土石坝中5mm以下颗粒含量作出了20%～50%之间的不同规定［16-18］。5 mm以下的颗粒反映在土石料图像中呈现出细小、黏连、形状不规则、堆叠现象严重的特征。对于此类图像，传统图像识别主要采用阈值化［19］、边缘检测［20］和分水岭［21］等方法，深度学习图像识别主要采用全卷积神经网络［13］、视觉几何群网络［22］、深度残差网络［14］、生成对抗网络［23］等语义分割方法。在采用不同方法试验后发现：针对土石料图像，传统识别方法精度较差，尤其是对5 mm以下颗粒识别困难。深度学习方法的识别精度主要依靠模型设计与标记的样本数量，土石料图像中存在大量的土石料颗粒，样本标记过程费时费力，且模型结构复杂运行耗时，对计算机硬件要求高，方法限制较多。

针对传统图像识别方法精度差，深度学习方法效率低的缺陷，本文结合在传统图像识别方法中广泛使用的基于最大类间方差阈值化的边缘检测算法［19］与基于深度学习的卷积神经网络模型，建立了一种土石料图像快速识别与级配智能分析模型，深度阈值卷积模型（Deep Otsu Convolutional Neural Network，DO-CNN）。经试验验证，模型能够显著提高级配检测的精度，且计算效率较高。

2 深度阈值卷积模型基本原理

2.1 边缘检测与最大类间方差法深度阈值卷积模型基于最大类间方差法（Otsu法）进行土石料图像的颗粒边缘检测。图像中的边缘是指图像局部灰度剧烈变化的区域，在处理过程中，可将图像抽象为二维函数f（x，y），其中x与y代表各点在图像中所处位置，幅值f即为各对应点的像素值，也称灰度值，取值范围为0～255，对彩色图像，处理时需首先转化为灰度图像。如图1所示，灰度变化主要表现为阶跃型、屋顶型两种不同的类型，寻找图像中具有阶跃型与屋顶型变化的点集即为图像的边缘检测［24］。

图1 不同类型的灰度渐变图与灰度变化过程

由图1 可知，图像灰度变化的剧烈程度可通过各方向上的梯度体现，对图像f（x，y）则其梯度∇f可以表示为：

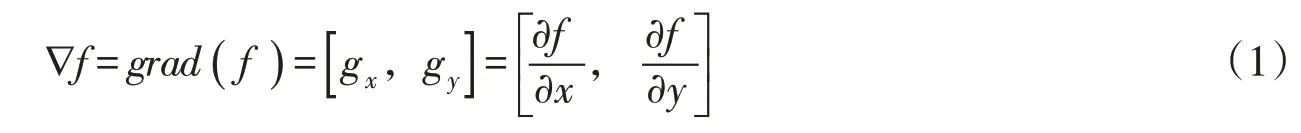
式中gx、gy分别代表x与y方向上的梯度。此时图像梯度的大小M（x，y）及方向a（x，y）可以表示为：

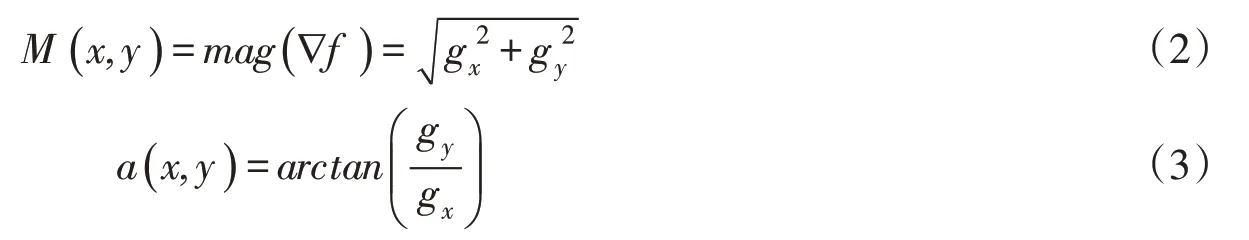
分析各点梯度的大小及方向，提取梯度值突变的各点，即可得到图像中的边缘特征信息。在图像进行边缘检测的过程中，常需对灰度图像进行阈值化处理，以加强区域的边缘特征，减小噪声信息的影响，以牛顿的画像为例，其基本过程如图2所示（图2（a）来源：https：//baike.baidu.com/item/%E8%89%B E%E8%90%A8%E5%85%8B%C2%B7%E7%89%9B%E9%A1%BF）。

图2 图像边缘检测基本过程

本文采用最大类间方差阈值化算法作为图像边缘检测的基础。最大类间方差法是一种以目标类与背景类之间灰度值方差最大化为标准的阈值化分割算法［25］。对土石料图像，目标类即为土石料颗粒所处区域，背景类即为颗粒边缘及阴影部位所处区域。假定图像f（x，y）的最大灰度值为L，其中灰度值为i的像素点个数为n，总像素点个数为N，则像素点灰度值为i的概率pi为：

取某一阈值k，将土石料图像分为两类，其中像素灰度值大于k的称为前景目标区域，小于k的称为背景边缘区域。此时两类区域出现的概率可以表示为：

式中：w1为背景区域出现的概率；w2为目标区域出现的概率。此时背景区域与目标区域内的平均灰度为：

式中：u1为背景区域平均灰度；u2为目标区域平均灰度；uT为土石料图像整体平均灰度。两类区域的类间方差可以表示为：

以遍历的方式对阈值k进行迭代，以类间方差σ2取得最大值时对应k值为最佳阈值，将背景区域灰度值以0（黑色）取代，将目标区域灰度值以255（白色）取代，即完成了土石料颗粒的基本分割过程，结合最大类间方差法与边缘检测算法，即可实现土石料颗粒的轮廓特征提取。

2.2 卷积神经网络由于土石料颗粒尺寸较小，在搬运过程中会产生翻滚、掩盖等现象，故经图像识别获取的级配有一定误差。但对同一开采条件下同一级配土石料，不同颗粒分布状态下的图像通过识别所得级配理论上应保持一致，故可以通过人工智能算法总结图像识别结果的误差分布规律，实现误差修正。级配数据的误差分布规律与其所处的粒径范围有一定关系，故深度阈值卷积模型采用可提取数据局部特征的卷积神经网络（CNN）作为误差修正的模型。

图3 卷积过程示意

卷积神经网络是一种具有卷积结构的深度神经网络，基本结构包括输入层、卷积层（convolution⁃al layer）、池化层（pooling layer）、全连接层（fully connected layer）及输出层［26-27］。如图3所示，在卷积层中，卷积核在上一层输出的特征图上滑动，与卷积核对应区域内各元素乘积求和，经偏置纠正与激活函数激活，即得到一次输出，通过对卷积核大小的调整，即可获得数据的局部特征信息［28-29］，其计算过程如下式所示：

池化层通过降低特征面的分辨率来获得区域内数据的不变特性［30］。本文中采用最大池化（Max⁃pool），即在池化层中保留池化核范围内最大值的方式进行池化。卷积层与池化层交替设置构成神经网络的多层中间隐含层，实现对区域数据特征的高维概括，而后在全连接层中，利用与上层输出的特征图同等大小的卷积核与上层所有输出进行卷积，从而实现对整个特征图的概括，以作为输出。

3 深度阈值卷积模型构建

3.1 模型框架深度阈值卷积模型通过阈值化算法对土石料图像进行快速分割，基于边缘检测算法提取图像中颗粒的轮廓信息，统计分析颗粒轮廓信息，即得到初始级配数据。以初始级配作为卷积神经网络的输入并进行模型训练，对初始级配误差进行修正，得到准确的级配数据，即实现了基于图像的土石料级配快速检测。模型的运行逻辑框架如图4所示。

图4 深度阈值卷积模型逻辑框架

3.2 图像数据采集与识别不同岩性的土石料之间有明显的色泽、形状差异，其图像识别的结果也具有差别。本文采用工程中广泛使用，色彩较为灰暗，对图像识别难度较高的灰岩石料作为土石料典型样本，以验证模型的识别效果。

结合实际工程环境与模型建立的需求，对土石料试样进行一定比例缩小［31-32］，以60 mm作为最大控制粒径，1 mm作为最小控制粒径，为简化数据处理过程，取1 mm以下颗粒含量占总体的0%，60 mm以下颗粒含量占总体的100%。采用筛分机进行标准筛分试验，获得土石料图像及其对应的真实级配，考虑施工现场环境，采用ACA1920-50GC 型工业相机作为图像采集工具，同时为减小光照条件影响，设置辅助照明系统以确保图像亮度与清晰度［12］。

DO-CNN模型基于开源图像处理函数库OpenCV，采用阈值化与边缘检测算法对土石料图像进行识别，过程如图5所示，主要包括：（1）采用最大类间方差法确定最佳阈值，划分颗粒区域；（2）确定腐蚀与膨胀结构单元，对阈值化图像进行腐蚀与膨胀的形态学处理，确定土石料边缘；（3）对土石料图像进行Canny边缘检测；（4）提取并分析土石料颗粒轮廓信息。

在图像处理过程中，为保证模型识别的准确性，首先对图像进行预处理，使得图像具有统一规格，减小图像因光照、角度等噪声信息影响。然后采用最大类间方差法进行阈值化处理，如图5（b）所示，此时土石料颗粒间存在大量的黏连现象，代表目标颗粒的白色区域之间相互贯通，无法对颗粒范围进行准确划分。为解决颗粒之间的黏连，采用图像腐蚀，即缩小土石料所处区域，再通过图像膨胀，即扩张各区域边缘，以恢复颗粒形状的方式，实现颗粒区域划分。最后采用Canny边缘检测算法进行轮廓检测，即可获得颗粒的形状信息。对不规则的多边形土石料轮廓，常采用椭圆拟合，以其短轴长度作为颗粒可通过筛分孔径的最小直径［33-35］，以此划分各颗粒所属粒径范围。针对同一料场获取的土石料，其母岩岩性能够基本保持相似，故假设样本密度均匀且一致，分析不同粒径范围内颗粒的多边形面积信息及其占比，即可得到初始级配数据。

图5 DO-CNN模型中的图像识别过程

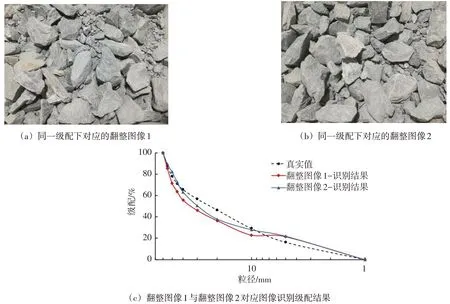
图6 同一级配下翻整后形成的土石料图像及级配识别结果

由图5可知，由于图像识别算法的限制，在图像形态学处理过程中，代表边缘及阴影区域的黑色部分增加，部分颗粒信息丢失，识别结果与原始图像存在一定的差异。故初始级配虽能体现级配分布的基本规律，但仍存在部分误差。为降低信息丢失对识别结果的影响，模型设置多次不同强度的腐蚀与膨胀，对各强度下的颗粒轮廓进行求交分析，保留交集为空的颗粒轮廓，从而在消除黏连现象的同时补充因形态学处理丢失的信息，减小图像处理导致的误差。同时，土石料在运输过程中不可避免的产生翻滚、遮盖现象，导致同一级配的土石料颗粒分布状态有所差异，相应图像经识别所得级配结果也不相同。如图6（a）与图6（b）为同一级配条件下，经翻整处理形成的土石料图像，对应图像识别所得级配如图6（c）所示，显然颗粒分布状态的差异也将导致级配检测的误差。为解决图像识别算法及颗粒分布状态导致的误差，采用卷积神经网络对识别所得级配进行训练修正。

3.3 卷积神经网络训练经试验验证，20次翻整处理后的土石料能够基本代表同一级配条件下，土石料的不同分布状态［12］，故对同一组土石料，本文采用经20 次翻整形成的图像作为一组识别样本。在试验中，对土石料取1、5、10、20、30、40、45、50、55和60 mm，共10种控制粒径，对应10种粒径范围的级配数据。通过基于阈值化的边缘检测算法获得各图像对应初始级配，排列同组样本的初始级配，形成规模为20×10 的数据矩阵，作为模型训练样本。以筛分试验获取的真实级配形成1×10的数据矩阵，作为训练样本的学习目标。通过卷积神经网络，对各组训练样本与学习目标进行对比分析，实现对初始级配的修正。需要说明的是，在测试与实际使用阶段，已训练完成的模型可直接对一张未经翻整的土石料图像进行检测，并对检测结果进行修正，得到准确的级配数据。

在训练过程中，因样本数据规格较小，经多层卷积后形成的特征矩阵会快速缩小，导致边缘数据特征丢失。故DO-CNN 模型在卷积过程中，对各中间隐含层特征矩阵边缘以0 进行填充（Pad⁃ding），防止特征矩阵缩小过快。对卷积神经网络的输出结果采用均方差损失函数（Mean Square Error Loss，MSELoss）进行误差分析，其计算如下式（12）所示：

式中：E为均方差损失；e为全连接层输出的预测结果；y为真实值；n为所有输出结果的总数量。

通过误差反向传播与权重调整，即获得训练完成的DO-CNN 模型。深度阈值卷积模型中的卷积神经网络结构如图7所示。

图7 DO-CNN模型中的卷积神经网络结构

3.4 模型评价采用平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）及决定系数（Rsquared，R2）作为深度阈值卷积模型的评价指标，其计算如式（13）、式（14）所示。平均绝对百分比误差代表了误差相对于真实值的大小，值越小误差越小。决定系数R2取值范围0～1，代表了结果的可靠程度，值越大结果越可靠。模型评价指标计算时，因程序对于1 mm及60 mm以下颗粒含量采用了预设定的方式，故不参与模型评价计算。

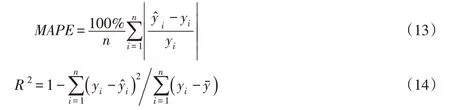
式中：n为样本数量；yi为第i个样本真实值；为第i个预测值；为样本的平均值。

4 深度阈值卷积模型检验与分析

4.1 试验设计为验证深度阈值卷积模型的准确性，采用筛分试验获取土石料真实级配并采集图像。本文共进行18组不同级配条件下的标准筛分试验，每组土石料翻整20次，获得18×20张不同的土石料图像。以其中16组图像作为模型训练样本，其余2组用于模型验证。经筛分试验获得的18组筛分级配如图8所示。

图8 18组标准筛分法所得级配曲线

4.2 模型参数选择DO-CNN模型在训练过程中的主要参数包括：epoch，代表模型训练过程中样本数据遍历次数，其取值大小与样本的多样性有关；iteration，代表一次遍历过程中的迭代次数，主要影响到模型训练效率；batch-size，代表每次遍历过程中投入的样本个数，主要影响到模型对样本的概化能力与模型的优化程度，其取值一般为2n；file-number，代表参与训练的样本总组数，即样本数量的大小；learning-rate，代表神经网络学习率，主要影响到模型的精度与训练效率，对训练完成的模型，learning-rate 不再产生影响，在训练过程中取值为0.0005。神经网络参数依靠模型预测结果的准确率进行选择，其最优参数并非为某一固定组合，对DO-CNN模型，主要为对参数epoch与batchsize 的选择，故对epoch 设置了小、一般、大、极大4 种不同的级别，即5、10、20、40 作为备选参数，batch-size取4、8、16作为备选参数。为验证神经网络中各参数对模型影响的一般规律，采用控制变量原则设置对照方案9组，并对比各方案对同一样本的检测结果，具体参数设置及级配检测结果评价如表1所示。

表1 9种方案下的试验参数设置及级配检测结果评价

对比9种方案下的模型检测结果可知：当训练样本数量较少时，即file-number取值为8时，方案7误差明显偏大；当epoch 与batch-size 取值较适合时，参数iteration对模型结果影响较小，两者同时偏大时，模型对于样本数据分布特征的提取能力下降，方案8误差增大；方案9在方案8的基础上继续增大epoch，虽然结果误差较小，但训练所需时间成倍增长；其他各组误差均处在较小的范围内，符合神经网络参数选择的一般规律。方案4检测结果误差最小，考虑到计算效率与准确度，以方案4对应模型参数进行深度阈值卷积模型训练与检测。

4.3 模型检测结果通过对16组共320张图像的识别与训练，DO-CNN模型能够总结图像识别结果的误差特征及同一级配条件下，不同颗粒分布状态的土石料级配分布规律。为验证模型的检测效果，以标准筛分试验所得级配真实值为评判依据，采用训练过的DO-CNN 模型对2组未参与训练的土石料图像进行级配检测。同时，因目前尚未有较成熟的方法可实现土石料图像的准确识别，故仅以基于最大类间方差法的边缘检测模型对同一验证样本进行检测，以作为DO-CNN模型的对照，其结果如表2所示。DO-CNN模型图像识别结果如图9所示。

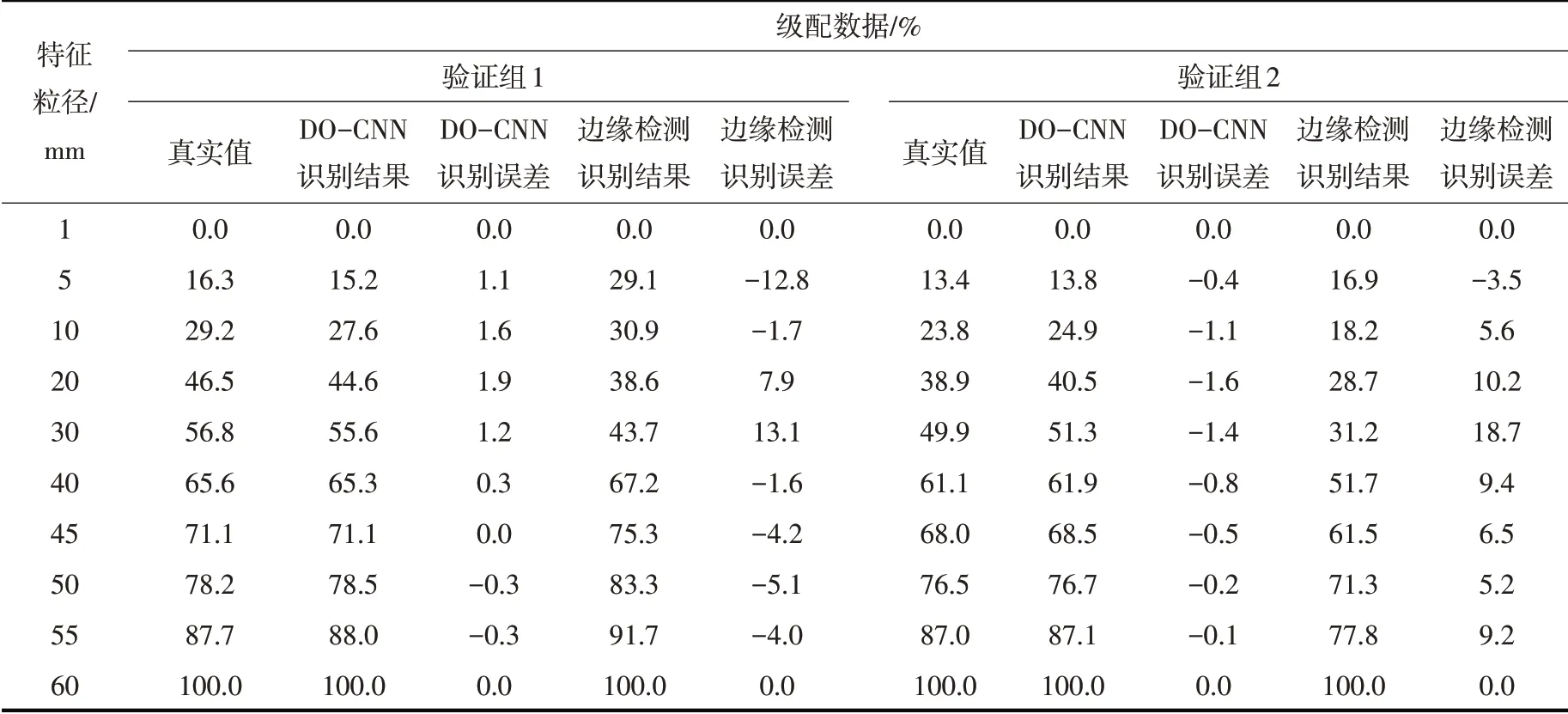
表2 DO-CNN模型与阈值化模型级配检测结果

图9 DO-CNN模型图像识别结果

4.4 结果对比与分析由4.3节可知，分别采用深度阈值卷积模型与基于阈值化的边缘检测模型对2组土石料图像进行检测，所得级配曲线如图10所示。两种模型级配检测结果的平均绝对百分比误差（MAPE）与决定系数（R2）如表3所示。

分析边缘检测模型与DO-CNN 模型级配检测结果，与标准筛分法所得真实级配相比，边缘检测模型误差明显偏大，其结果的平均绝对百分比误差最大值为19.46%，且边缘检测模型对10 mm 及5mm以下颗粒含量的检测结果较为接近，无法作为5 mm以下颗粒含量的判断依据。深度阈值卷积模型在图像识别过程中产生了部分颗粒信息丢失的现象，其识别结果较原始图像产生了一定的误差，但通过神经网络的训练修正，级配检测结果的误差明显减小，与真实值较为接近，平均绝对百分比误差最大值为2.45%。对5 mm以下颗粒含量，模型最大识别误差为1.1%，同样具有较高的准确率。

表3 DO-CNN模型与阈值化模型检测结果评价

图10 DO-CNN模型与阈值化模型级配检测结果

5 结论与讨论

本文结合基于最大类间方差的边缘检测算法与卷积神经网络，建立了土石料级配智能检测的深度阈值卷积模型（DO-CNN），并通过标准筛分试验获取土石料图像及级配数据用于模型训练与验证，以平均绝对百分比误差（MAPE）及决定系数（R2）评价了模型检测效果。研究证明，DO-CNN模型基于最大类间方差法进行图像快速分割与边缘检测，结合卷积神经网络保证级配检测的准确性与稳定性，实现了基于图像的土石料级配快速检测。成果表明，采用图像识别技术可近似确定筑坝砂、砾和堆石料的级配，能满足施工现场质量控制过程中快速、高效的需求。作为图像识别方法在确定筑坝材料颗粒级配中应用的基础性研究，本文取得了与级配真实值相近的研究成果，但仍属于初步研究阶段，后续还需进一步完善技术细节以投入生产实践。对模型总结及后续研究方向讨论如下：（1）深度阈值卷积模型（DO-CNN）能够实现基于土石料图像的级配快速检测，且检测结果准确率较高，对于5 mm 以下土石料颗粒，模型检测效果同样较好；（2）DO-CNN 模型基于深度学习模型建立，其准确率受样本数量与质量的影响，在工程应用过程中需对现场进行一定量的土石料图像采样，以进行模型初期训练，而后随着检测的进行，样本数量不断增加，模型检测精度也将不断提高；（3）本文在研究过程中采用1～60 mm粒径范围内大小较为均匀的土石料颗粒，未考虑在实际工程可能出现的极小颗粒与极大颗粒混合的粒径不均匀情况，有待结合工程现场情况进行研究与改进；（4）含水量对土石料形态有重要影响，不同含水状态下土石料呈现的图像各不相同，同时拍摄角度与光照等因素也会导致图像差异，不同的土石料图像对图像识别算法提出了更高要求。未来将从含水量、图像采集环境、改进图像识别算法等方向进一步研究，以增强模型的实用性与适用性。