城市屋顶降雨径流过程单位线模型研究

申红彬，徐宗学，李灵军，郝秀平

（1.华北水利水电大学，河南郑州 450045；2.北京市水科学技术研究院北京市非常规水资源开发利用与节水工程技术研究中心，北京 100048；3.北京师范大学水科学研究院城市水循环与海绵城市技术北京市重点实验室，北京 100875；4.水利部综合事业局，北京 100053）

1 研究背景

城市屋顶是城市地表中一种重要的类型单元，按透水性质总体可以划分为不透水屋顶与绿色（渗透）屋顶。单位线法作为一种重要的概念性水文模型，较早就应用于城市地表（包括不透水屋顶）降雨径流过程的模拟［1-2］，径流输出对降雨输入的函数响应关系明确。不过，对于绿色屋顶降雨径流过程的模拟，现今单位线法尚少有涉及。如今，对于绿色屋顶降雨径流过程的模拟，主要基于描述土壤水下渗的Richards方程进行数值模拟，相关模型有Hydrus-1D、SWMM-2D等［3-5］，涉及参数较多，求解过程复杂，难以直观反映出径流结果和降雨条件之间的响应关系。

鉴于Richards方程的复杂性，不少学者提出了不同的简化方程［6-8］，但这些方程均以假设下渗土柱为半无限长作为定解条件，并多忽略下渗土柱表面积水变化的影响，主要关注土柱内土壤水长时间的下渗过程。然而现实中绿色屋顶用于雨水渗蓄的基质土壤层的厚度是有限的［9-10］。如果降雨强度比较小，绿色屋顶在有限厚度的基质土壤层达到饱和前不会产生径流，基质土壤层达到饱和后的渗流经排水层排出的过程即为径流过程，且该径流（渗流）过程更易受到基质土壤层表面降雨（积水）过程变化的影响。因此，基于绿色屋顶基质土壤层厚度有限性的特点，结合土壤下渗简化模型，考虑表面降雨（积水）过程变化对径流（渗流至排水层出流）过程的影响，能否建立反映降雨-径流响应关系的单位线模型，就成为一个有待研究的问题。通过建立绿色屋顶降雨径流过程的单位线模型，再联合不透水层顶降雨径流过程的单位线模型，两者将可共同构成城市屋顶降雨径流过程的单位线模型。并且，在同类模型的基础上，通过比较绿色屋顶与不透水屋顶模型参数的区别，更便于从本质上认识两类屋顶降雨径流过程的差别。

本文基于土壤水饱和下渗理论，针对绿色屋顶降雨产（径）流特点，推导建立绿色屋顶降雨径流过程的单位线模型，并联合不透水层顶降雨径流过程的单位线模型，共同构成城市屋顶降雨径流过程的单位线模型；再根据不透水屋顶与绿色屋顶降雨径流过程实测资料，分别进行了模拟应用，并在同类模型的基础上，对两类屋顶降雨径流过程模拟中的模型参数进行了比较与分析。

2 模型构建

2.1 不透水屋顶降雨径流过程的单位线模型城市不透水屋顶一般汇水面积较小，降雨径流过程可选用单一线性水库的Nash单位线模型。Nash瞬时单位线数学表达式通常表示为：

式中：u（0，t）为瞬时单位线；t为时间；K为线性水库调蓄参数。

对瞬时单位线通过S积分变换，可转换为离散时段单位线形式为：

式中：q（Δt，n）为时段单位线；Δt为单位线时段；n为时段序号。

相应出口断面流量过程为：

式中：Q（n）为出口断面流量，转化为单位时间径流深（流量与汇水面积相除）单位，mm/min；n为出流时刻；i为计算时段序号；I（i）为净雨强度，mm/min。

式（1）中线性水库调蓄参数K等于屋顶坡面汇流时间τ：

式中：τ为坡面汇流时间，s；L为坡面长度，m；V为坡面水流平均流速，m/s。

研究表明，坡面水流平均流速V影响因素较多，包括坡度、糙率、雨强等，影响机理十分复杂，近似可以采用Eagleson-Bra公式进行估算［11］：

式中：J为坡面比降；n为糙率；A为坡面面积，km2；B为坡宽，m；I为降雨强度，cm/h。

2.2 绿色屋顶降雨径流过程的单位线模型根据土壤水饱和下渗理论，下渗土柱上的作用合力包括：表面积水深、下渗土柱长度、湿润锋处毛管上升高度以及空气剩余压力。假设绿色屋顶基质土壤层厚度为l，在基质土壤层饱和产流后，重点考虑表面积水深影响，忽略湿润锋处毛管上升高度及空气剩余压力项，则下渗速率可以根据Darcy定律表示为式（6）形式，并经排水层排出转化为径流过程：

式中：fp（t-t0）为产流后土壤下渗速率，mm/min；Q（t-t0）为排水层出流速率，转换为单位时间径流深单位，mm/min；hp（t-t0）为表面积水深，mm；l为基质土壤层厚度，mm；H（t-t0）为作用水头，mm；Ks为饱和水力传导度，mm/min；Kd为系数，min-1；t为时间，min；t0为饱和产流时间，min。

对于作用水头H（t-t0），根据质量守恒原理存在如下平衡方程：

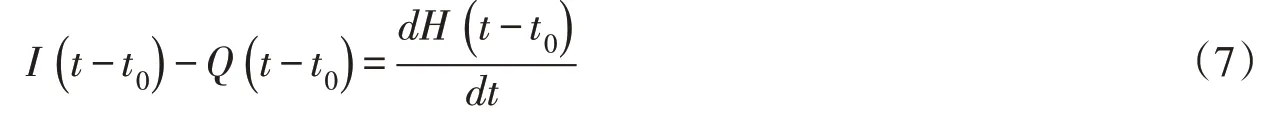
式中：I（t-t0）为饱和后产流后降雨强度，mm/min。

联合求解式（6）和式（7），可以得到绿色屋顶产流后径流过程的连续卷积形式：

其中瞬时单位线u（0，t）的表达式为：

流量过程表示为离散形式为：

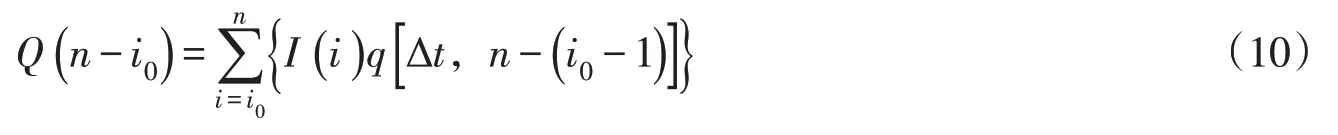
式中i0为产流开始时段序号。

2.3 两类屋顶降雨径流单位线模型方程统一形式综合以上，分别建立了城市不透水屋顶降雨径流过程的单位线模型与绿色屋顶降雨径流过程的单位线模型，两者共同构成了城市屋顶降雨径流过程模拟的单位线模型。进一步比较不透水屋顶与绿色屋顶降雨径流过程及相应单位线模型式（3）和式（10），两类屋顶虽然降雨径流过程形成机理不同，但模型描述使用的数学方法种类相同，因此可以将城市屋顶降雨径流过程单位线模型方程表示成更为统一的数学表达形式，不同之处在于两类屋顶的模型参数计算方法与物理意义有所不同，具体结果如表1所示。可以看出，单位线模型方程经过统一数学表达形式后主要包括两个参数：径流输出对降雨输入的响应速率β与径流（产流）起始时段序号i0，并且对于不透水屋顶与绿色屋顶的模型参数选择不同：（1）在不透水屋顶中响应速率β是坡面汇流时间（坡长除以坡面平均流速）的倒数，径流损失主要为填洼损失，产流时间较短，相应i0等于或略大于1；（2）在绿色屋顶中响应速率β则是基质土壤层稳渗时间（基质土壤层厚度除以饱和水力传导度）的倒数，并且只有在基质土壤层达到饱和后才会产生径流，产流时间较长，相应i0多大于1。

表1 不同类型屋顶降雨径流单位线模型统一形式与参数比较

3 模型应用

3.1 城市不同类型屋顶降雨径流过程监测2015年6—9月期间，在北京市水科学技术研究院内开展多种类型屋顶降雨径流现场试验监测，位置与布置如图1（a）所示。其中，监测不透水平面屋顶面积约为96 m2，屋顶铺设有防水油毛毡；绿色屋顶（绿化比例为100%）面积约为65 m2，垂向结构可参见图1（b），具体设计如下：（1）植被层草种选择佛甲草，具有抗旱节水、隔热降温、易于管理等特点；（2）基质层采用草炭土、蛭石和砂土混合而成的填料，厚度为6 cm，配比为4∶2∶1，具有重量轻、透水性好、持水性好、性能稳定、养护方便等特点；（3）过滤层位于基质层底部，材料为过滤布（厚度1～2 cm），防止介质流失；（4）排水层厚5 cm，用轻质塑料制成，均匀布置碗状结构以承载径流，并有排水出口。试验过程中，屋顶降雨过程监测主要通过屋顶安装雨量计，可以获得1 min和5 min雨量值；径流过程监测采用“液位计+三角堰”测量方法，可以对水位及流量进行连续监测。各个试验屋顶排水管出口下方均配有一套三角堰测流槽装置（参见图1（c）），槽内安装液位计，液位计选用美国生产的Global Water WL-16 压力液位计，恒温条件下测量精度为±0.1%满量程，三角堰顶角角度为30°，平面屋顶三角堰堰底面积为0.48 m2，绿色屋顶三角堰堰底面积为0.4 m2。三角堰流量计算在溢流前为时段始末水位差值与堰底面积的乘积，溢流后过堰流量采用Kindsvater-Shen公式计算［12］：

式中：Q堰（t）为三角堰过堰出流流量，m3/s；θ为三角堰顶角，30°；CD为流量系数，取值为0.6；He为堰上水头，m；g为重力加速度，m/s2。

监测期间，共计监测到11场有效降雨径流数据，具体统计如表2所示。表2 中，不透水屋顶填洼深损失与绿色屋顶截留深（包括：植物截留、基质渗持、植物蒸散发、基质蒸发量）［13-16］损失主要根据水量平衡原理，采用降雨量与径流深的差值计算。其中，不透水屋顶填洼损失综合受到前期降雨填洼深、间隔干旱天数、场次降雨量等因素的影响，绿色屋顶截留损失综合受到前期降雨截留深、间隔干旱天数、场次降雨量、植被生长状况等因素的影响。将不同场次降雨量按从小到大排序分别绘制不透水屋顶填洼深与绿色屋顶截留深随降雨量的变化过程（参见图2和图3），可以发现：绿色屋顶最大截留深基本稳定在28 mm左右；不透水屋顶最大填洼深约为13 mm，相对较大可能是因为屋顶建成时间较长表面坑洼不平、且靠边原建有一道隔墙挡水所致（参见图1）。对于不透水屋顶某场次降雨，当前期洼蓄水量为0时，填洼深随降雨量的变化过程近似可按Linsley公式计算：

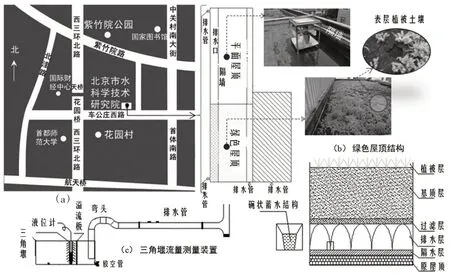
图1 监测屋顶布置示意

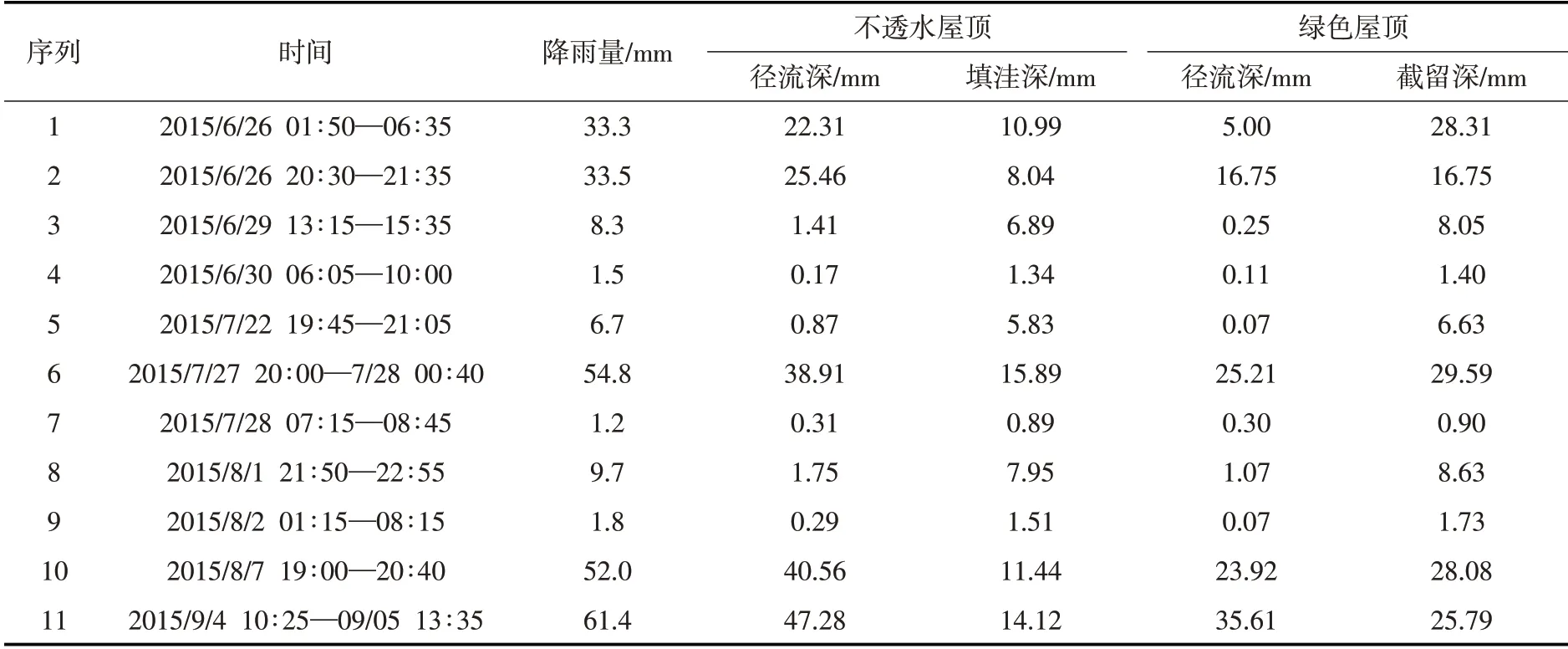
表2 不透水与绿色屋顶降雨径流监测

式中：Δ为不透水屋顶填洼深损失，mm；Δmax为不透水屋顶表最大填洼深损失，mm；k为变化速率，k=1/Δmax；P为降雨量，mm。

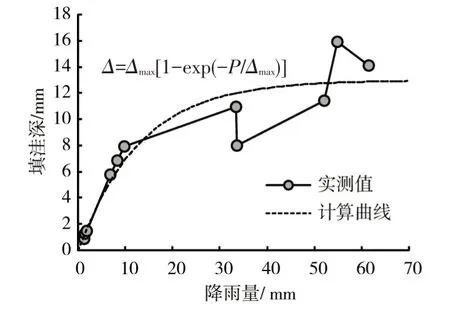
图2 不透水屋顶填洼损失变化情况

图3 绿色屋顶截留损失变化情况

3.2 屋顶降雨径流过程模拟应用基于表1中建立的城市屋顶降雨径流过程单位线模型方程统一形式，分别对不透水平面屋顶与绿色屋顶降雨径流过程进行模拟应用。

为便于确定模型径流（产流）起始时间，本次模拟主要对前期干旱天数较长（≥5 d），且降雨量大于绿色屋顶最大截留深（28 mm）的场次降雨径流过程进行模拟，以尽量保证不透水屋顶前期填洼蓄水量足以减少至0，绿色屋顶截留深可以达到最大值。因此，选择降雨序列1（2015/6/26 01∶50—06∶35）、降雨序列6（2015/7/27 20∶00—7/28 00∶40）以及降雨序列10（2015/8/7 19∶00—20∶40）进行模拟，相应不透水屋顶实测填洼深均在10 mm以上、绿色屋顶实测截留深均在28 mm左右（参见表2）。

基于表1，对不同类型屋顶模型参数分别确定如下：（1）不透水平面屋顶。响应速率参数β：不透水平面屋顶模型响应速率β主要与屋顶调蓄参数K有关。对于不透水平面屋顶调蓄参数K值，相当于屋顶汇流时间，基于式（5）计算坡面水流平均流速，根据相关屋顶排水设计规范，坡度取值为2%，降雨强度采用平均雨强，糙率综合考虑屋顶材料、隔墙挡水及排水口缩窄局部阻力影响，取等效糙率为0.17，采用式（4）计算汇流时间。径流（产流）起始时段序号i0：对于不透水平面屋顶径流（产流）起始时间，可以通过比较累计降雨量与填洼损失量确定，对于本次模拟工况，填洼损失采用式（12）计算，经检验计算结果与实测径流（产流）起始时间基本符合（参见图4）。（2）绿色屋顶。响应速率参数β：绿色屋顶模型响应速率β主要与响应参数Kd有关。对于绿色屋顶响应参数Kd值，经过率定取值为0.2，对应饱和水力传导度Ks值为12 mm/min，数值较大可能是因基质层土壤内混合含有砂土有关。径流（产流）起始时段序号i0：对于不同场次降雨绿色屋顶径流（产流）起始时间，因基质土壤层初始含水率（综合受到前期降雨截留深、间隔干旱天数、植被生长状况等因素影响）不同而会有所区别，需要参考表2中不同场次降雨实测截留深与累计降雨量比较确定。对于本次模拟工况，可以根据场次降雨累计降雨量与最大截留深（28 mm）比较确定，经检验计算结果与实测径流（产流）起始时间基本符合（参见图5）。

为检验模型模拟效果，选用2种评价指标［17-19］：（1）确定性系数R2。回归分析是模型效果评价最为基本的定量分析方法，利用Excel软件对流量计算值与实测值进行线性回归，可以直接得到回归方程的确定性系数R2值。R2值越趋近于1，说明流量模拟值与实测值拟合越好；（2）Nash-Sutcliffe 效率系数（NSE）。NSE效率系数主要用于水文模型效率评价，是判定残差与实测值数据方差相对量的标准化统计值。NSE值一般在-∞～1之间，当NSE=1时说明流量计算值与实测值完全吻合，当0＜NSE＜1时说明计算效果在可接受水平内，当NSE≤0时说明流量计算值与实测值存在较大偏差。NSE效率系数计算表达式为：

式中：NSE为Nash-Sutcliffe效率系数；为流量实测值，mm/min；为流量模拟值，mm/min。

以降雨序列1（2015/6/26 01∶50—06∶35）、6（2015/7/27 20∶00—7/28 00∶40）、10（2015/8/7 19∶00—20∶40）为例，分别对不透水平面与绿色屋顶降雨径流过程进行模拟，如图4和图5所示。图中纵坐标值是在式（10）基础上，两侧同乘Δt（5 min），转化为时段降雨量、径流深。可以看出，计算值与实测值变化趋势符合。综合所有降雨径流计算值与实测值，确定性系数R2与NSE效率系数值分别达到0.89、0.89（不透水屋顶）和0.84、0.85（绿色屋顶），模拟效果良好。

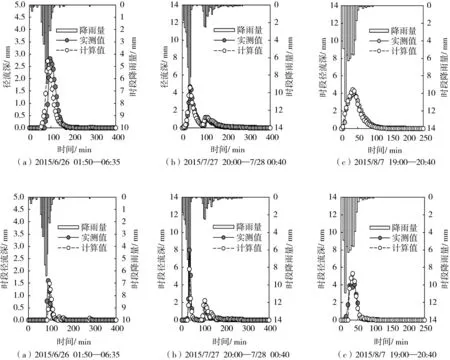
图4 不透水屋顶降雨径流过程模拟

图5 绿色屋顶降雨径流过程模拟

3.3 不同屋顶模型参数比较分析基于表1 中城市屋顶降雨径流过程单位线模型方程的统一形式，比较模拟工况下不透水平面屋顶与绿色屋顶在降雨径流过程模拟中的模型参数取值变化情况，如表3所示。可以看出：不同类型屋顶模型响应速率β与径流（产流）起始时间i0参数取值均存在较大区别。对于不透水平面屋顶，径流（产流）起始时间i0基本为1或2，响应速率β值为0.05与0.06，对于绿色屋顶，径流（产流）起始时间i0在5～18之间，响应速率β值为0.2。绿色屋顶的径流（产流）起始时间明显晚于不透水平面屋顶，说明绿色屋顶具有更强的雨水蓄存能力，但绿色屋顶模型响应速率参数大于不透水平面屋顶，说明不透水平面屋顶经隔墙阻水调节作用后，对降雨输入过程具有更好的调峰削减效果。如果降雨峰值时间位于绿色屋顶饱和产流时间之后（2015/7/27 20∶00—7/28 00∶40），则绿色屋顶相比不透水屋顶将难以产生较好的调峰削减效果，见图6（a）。因此，绿色屋顶对降雨径流过程的削减效应更多依赖于基质土壤层对前期降雨的截留（渗蓄）减水作用。

根据表1，绿色屋顶的模型响应速率β与基质土壤层厚度l和饱和水力传导度Ks有关。对绿色屋顶模型β值拟定不同的参数调整方案：（1）Ks一定、调整l，（2）l一定、调整Ks，参见表3。以降雨序列6（2015/7/27 20∶00—7/28 00∶40）为例，该降雨过程为双峰雨型，模拟计算不同的β值条件下绿色屋顶的降雨径流过程，如图6（b）（c）所示。计算过程中，假设绿色屋顶最大截留深与基质土壤层厚度l成正比，对图6（b）（c）比较可知，在绿色屋顶饱和水力传导度Ks一定情况下，增大基质土壤层厚度l更能有效增大前期雨水渗蓄量，并可显著削减径流过程前期峰值，不过对后期峰值的削减效应有所减弱。另外，从理论分析来看，增大基质土壤层厚度l（或减小饱和水力传导度Ks）可使模型响应速率参数β值减小，这会导致后期表面积水排水时间略有延长（参见图6（b）（c）局部）。因此，对于增大绿色屋顶基质土壤层厚度l的设计要综合考虑前期渗蓄雨量增多与后期排水时间延长的影响。

表3 不透水与绿色屋顶模型参数与调整方案

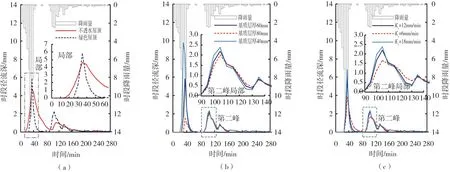
图6 不同参数方案下屋顶降雨径流过程模拟

需要指出的是，上述不同屋顶模型参数比较分析主要针对本次监测屋顶的模拟工况，前期干旱天数较长、场次降雨量较大，不透水屋顶填洼损失与绿色屋顶截留损失均基本达到最大值。实际上，对于不同场次降雨，两类屋顶径流损失的影响因素众多、变化规律复杂，这会直接影响模型径流（产流）起始时间参数的取值。需在进一步完善研究不透水屋顶与绿色屋顶径流损失规律的基础上，再通过与累计降雨量比较确定模型径流（产流）起始时间参数。对于模型响应速率参数，根据表1中参数物理意义，不透水屋顶在不同降雨强度、屋顶坡度、阻力特性等条件下需要分别加以确定，绿色屋顶则在不同基质屋厚度及材料组成等条件下需要分别加以确定。

4 结论

根据本文的模拟计算与分析，可以得到以下几点结论：（1）城市不透水与绿色（渗透）屋顶的降雨径流过程均可采用单位线模型进行模拟，并可采用统一的数学方程形式表示，参数包括响应速率参数与径流起始时间。对于不同类型屋顶，模型参数计算方法与物理意义有所不同。其中，不透水屋顶的响应速率参数为坡面汇流时间的倒数，绿色屋顶的响应速率参数则为基质土壤层稳渗时间的倒数。（2）结合城市不透水平面屋顶与绿色屋顶降雨径流过程的实际监测数据，选择模拟工况，采用单位线模型分别对两类屋顶的降雨径流过程进行模拟，并选用确定性系数R2与NSE效率系数对模拟效果进行评价。结果表明，计算值与实测值变化趋势符合良好，确定性系数R2与NSE效率系数值分别达到0.89、0.89（不透水屋顶）和0.84、0.85（绿色屋顶），初步验证了所建模型的合理性。（3）对绿色屋顶拟定不同的响应速率参数调整方案计算结果表明，在饱和水力传导度一定情况下，增大基质土壤层厚度能够有效增大前期雨水渗蓄量，并可显著削减径流过程前期峰值，但对后期峰值削减效应有所减弱，且会导致表面积水排水时间略有延长。因此，对绿色屋顶增大基质土壤层厚度要综合考虑前期渗蓄雨量增多与后期排水时间延长的影响。

后期，考虑到不透水屋顶与绿色屋顶径流损失影响因素众多、变化规律复杂，仍需在进一步完善研究两类屋顶径流损失规律的基础上，通过与累计降雨量比较确定模型径流（产流）起始时间参数，并对不同条件下的不透水屋顶（不同降雨强度、屋顶坡度、阻力特性等）与绿色屋顶（不同基质屋厚度及材料组成等），分别研究确定模型响应速率参数。对于城市地表而言，下垫面种类较多，除屋顶（不透水屋顶、绿色屋顶）外，还包括道路（不透水路面、透水铺装等）、绿地、水域等，不同种类下垫面的产汇流规律有所不同。因此，在城市降雨径流模拟中，应根据详细的土地利用和土壤属性分布数据，考虑降雨特征的时空变异性，分别采用与下垫面特征相匹配的产汇流理论，划分水文单元进行分布模拟［20］。本文所建模型为屋顶单元类子模型，可以再结合其它地表单元类子模型，共同构建城市地表降雨径流的分布式模型。