冰盖下典型复式断面河道水深平均流速的横向分布
2021-05-08邹德昊戴长雷郭显峰路锦枝
邹德昊,戴长雷,郭显峰,路锦枝
(1.黑龙江大学寒区地下水研究所,黑龙江哈尔滨 150080 2.黑龙江大学水利电力学院,黑龙江哈尔滨 150080;3.流域水循环模拟与调控国家重点实验室中国水利水电科学研究院,北京 100038)
1 研究背景
天然河道的过流断面常常可概化为渠道复式断面的形式,在北方的冬季,一旦河道封冻形成冰盖,复式断面流速的分布规律就会发生改变,滩槽的阻力和输水能力都会受到影响,因此研究冬季冰封河道的流速分布规律对于凌汛防治具有重要意义。冰盖的出现增加了过水断面的湿周和阻力,使得河渠的断面流速分布和输水能力发生显著改变。当河渠为复式断面且冬季冰盖糙率不断发生变化时,如在漫滩水流中,由于主槽和滩地之间水力条件存在差别,使得交界面出现剪切层并强烈影响着各种水力参数的分布,因此采用一维模型计算可能产生较大的偏差。
现有研究采用二维k-ε紊流模型计算出复式断面河渠的横向流速分布。Shiono和Knight[1]提出的SKM法以水深平均的Navier-Stokers方程为基础,描述了复式河道断面的过流情况,给出了断面的横向沿水深方向平均流速的计算公式。许唯临等[2-3]从SKM法出发,将二次流项归并入雷诺切应力项,结合主槽与滩地的水深平均流速,推导出无冰盖复式河道横向流速分布和床面切应力分布的计算公式,并由实测数据给出了涡黏性系数的经验公式。吉祖德和胡春宏[4]的研究表明:在明流复式断面上,主槽和滩地平衡区的垂线流速服从对数律公式,但是,在边壁区,流速不再服从对数分布,其最大流速不在水体表面,而是有所下移。杨开林[5]研究了水流的非均匀性对矩形河渠水深平均流速横向分布的影响,算例表明,在实际流动为非均匀流的情况下,采用SKM模型计算的流量存在很大的偏差,提出了改进的非均匀流计算模型。刘沛清和冬俊瑞[6]探讨了复式断面渠道中主河槽和滩地之间水流的动量传递机理,应用动量定理导出了复式断面渠道中恒定均匀流的计算公式,并与实验资料进行了验证。Knight和Hamed[7]根据试验结果给出了具有直角突变床面的对称复式断面渠道的边界剪切力分布,并评估了子区域之间的动量传递对垂向和横向流速分布的影响。Peters和Dow[8]的研究表明对于冰封的复式断面渠道,湿周和水流阻力都会增大,过流能力会降低。杨克君和曹叔尤[9]总结了明流复式河槽流量计算的各种方法,运用这些方法分别计算整个复式断面的流量和滩槽流量分配;此外,杨克君[10-11]还分析了明流复式河槽的横向动量输移的原理并给出计算方法。以上关于复式断面河渠的计算方法都是针对无冰盖水流,但其对冰盖下水流的流动数学模型的建立以及规律的探求起到了至关重要的指导和推动作用。且目前尚未提出冰盖下复式断面河渠水流的简易有效计算方法。冰盖的形成改变了水流的流速分布,对于被冰覆盖的通道流动,以往研究主要集中于河道的横向水深平均速度[12]、过流阻力[13]和冰层覆盖对泥沙输移的影响[14]。河道水深平均流速是研究泥沙运动和河道演变预测的基础[15],通过横截面上深度平均流向流速的横向积分可以得到给定水位下的总流量。因此,研究冰盖下河渠流速分布、流量和二次流等流动特征是十分必要的。
本文提出了一种不必通过计算机编程联立求解复杂方程组即可求得水深平均流速的计算公式。首先根据质量守恒和动量守恒原理,以杨开林的准二维模型为基础[5,16-17],利用双层假设,首先将河道断面划分为上冰盖区和床面区,随后令二次流项并入雷诺切应力项中,将湿周产生的阻力体现在达西-维斯巴赫综合摩擦系数中,把斜坡区和漫滩区的水深平均流速直接联立。进一步推导出冰盖下典型复式断面恒定非均匀流的水深平均流速的横向分布的准二维模型;最后将计算结果与物理模型试验实测数据对比。
2 理论分析
2.1 冰盖下典型复式断面河道水流的准二维模型在一般情况下,综合阻力系数fd、无因次涡流黏度λ,二次流系数K或β等参数为y的函数,每个区间的水深平均流速可以用杨开林的准二维模型计算。需要根据边界条件的特点,通过编写计算机程序求解有限解析计算法,这个过程需要求解含递推公式的复杂方程组。具体求解方法见参考文献[16]。本文根据Shiono和Knight[1]的假设,忽略紊动应力在各个方向上的梯度,应用Abril和Knight[18]对二次流的描述,即沿着过水断面积分可得到杨开林[5]建立的冰盖下沿水深方向平均流速Ud沿横向y分布的准二维模型。
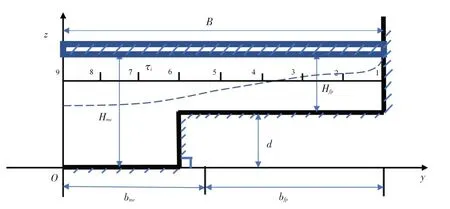
图1 冰盖下典型复式断面渠道示意图
如图1所示,对于复式断面主槽区和漫滩区,可得冰盖下复式断面渠道平槽区且冰厚均匀的解:

式中:Ud为沿水深方向的平均流速;A1、A2为待定常数;y为如图1所示的横向的距离,为综合阻力系数,;Hi为平槽区断面水深,其中:。b为主槽区的半宽,sh为水面坡降,s0为底坡,λ无因次涡流黏度,ρ为水的密度,ρice为冰盖的密度,hice为冰盖的厚度。符号的下角标“mc”和“fp”为别表示主槽区和漫滩区的物理量或中间变量。
当冰厚为均匀分布时,采用Ervine 利用大量实测资料确定的二次流系数的经验值,令有关各式中二次流系数K=0.0025[19]。由于所选取的复式断面渠道具有左右相互对称性,可以得到主槽区的待定系数A1=A2=Amc,漫滩区的待定系数A3=Afp,再由边界条件可以得到:
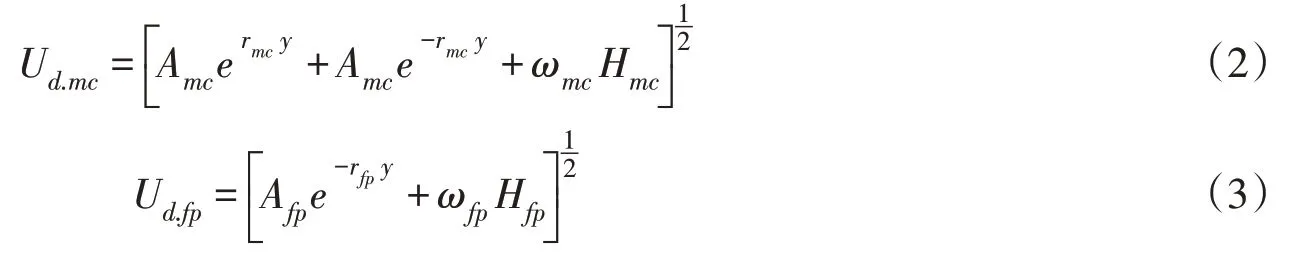
式中Ud下角标“mc”和“fp”为别表示主槽区和漫滩区的沿水深方向的平均流速。此外,主槽区及漫滩区相邻区域的相交处必须满足速度和速度梯度的连续性条件。令Ud.mc和Ud.fp的流速平滑相接。即在该处两曲线的函数值及梯度相等。联立求得:

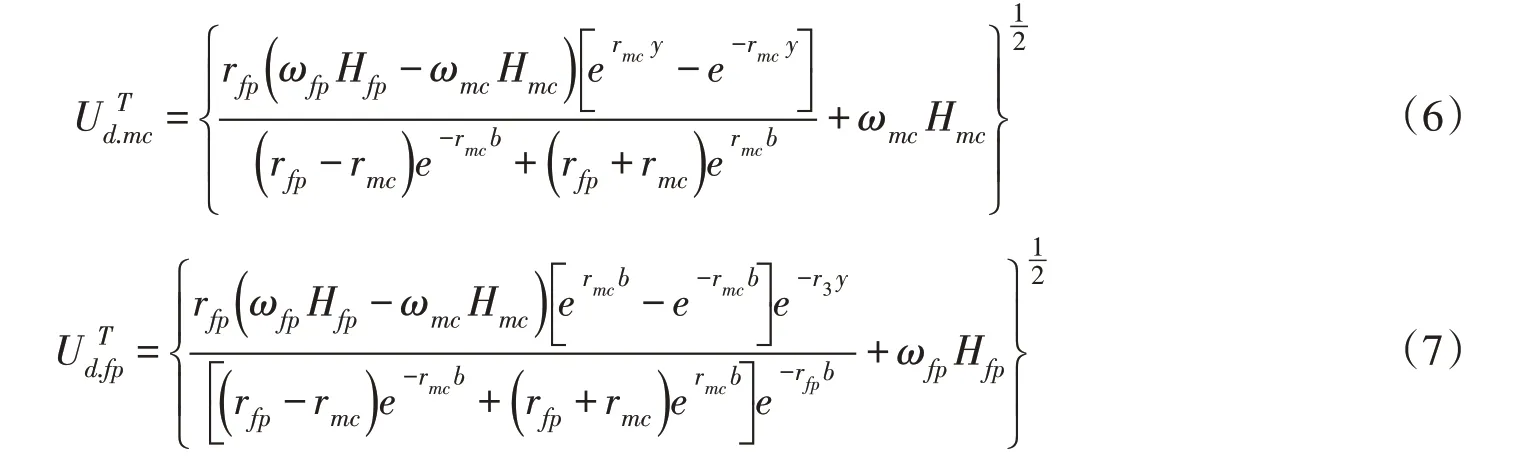
在时间T内通过断面的总流量可表示为:
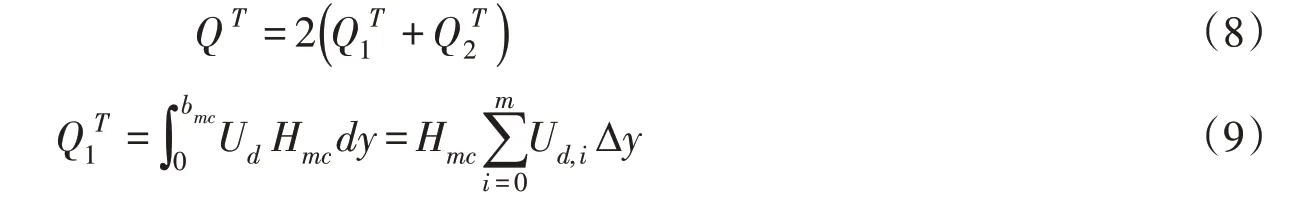
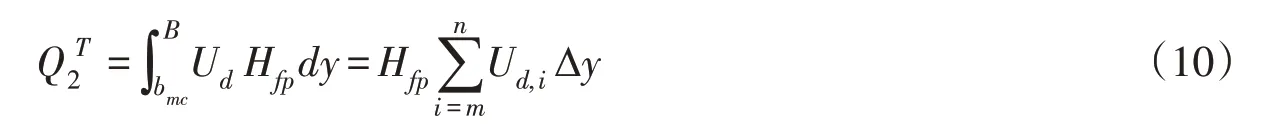
式中;Q为断面总流量;为主槽流量;为漫滩流量,m3/s;Hmc为主槽区的水深;Hfp为漫滩区的水深,m;Δy=B/(m+n),m为主槽的半宽断面分区数,n为漫滩区的分区数。
2.2 算例“T”型复式断面如图1所示,为半宽断面的示意图。其中bmc=0.15 m,bfp=0.45 m,B=0.6mB=0.6m,d=0.075m,漫滩水深分别为Hfp1=0.06m,Hfp2=0.08m。表1、表2为计算参数,计算得表3的成果可以和试验数据相比较。

表1 复式断面渠道特征参数

表2 计算参数

表3 计算所得各断面平均速度的横向分布Ud (单位:m/s)
3 试验验证
试验装置由主槽循环水箱、水泵、变频器、电磁流量计、推拉式水位控制尾门、消能装置和模型冰盖等组成,其中由于真冰的制作储存、尺寸需求、易碎性、控温的超高成本,所以在采用高密度聚氨酯泡沫作为模型冰代替真冰。它的优点是减少模型负重容易运输,容易切割,可塑性强,不会融化或者冻结。通过变频器对水泵进行精准控制、电磁流量计进行观测,从而可以在闭合循环水系统中来严格控制复式断面水槽的流量。消能装置用于消耗水流垂直方向的动能确保水流均匀稳定,水位可通过安装在下游的尾门的开闭尺度进行调节。如图2为实验装置的刨面图,主槽长20 m、宽1.2 m。实验采用有机玻璃搭建的模型渠道,在渠道底部每3 m 设置一个测压管口,共5 个测压管。通过精度为0.1 mm的测针所得测压管的水位高程判断水面坡降。
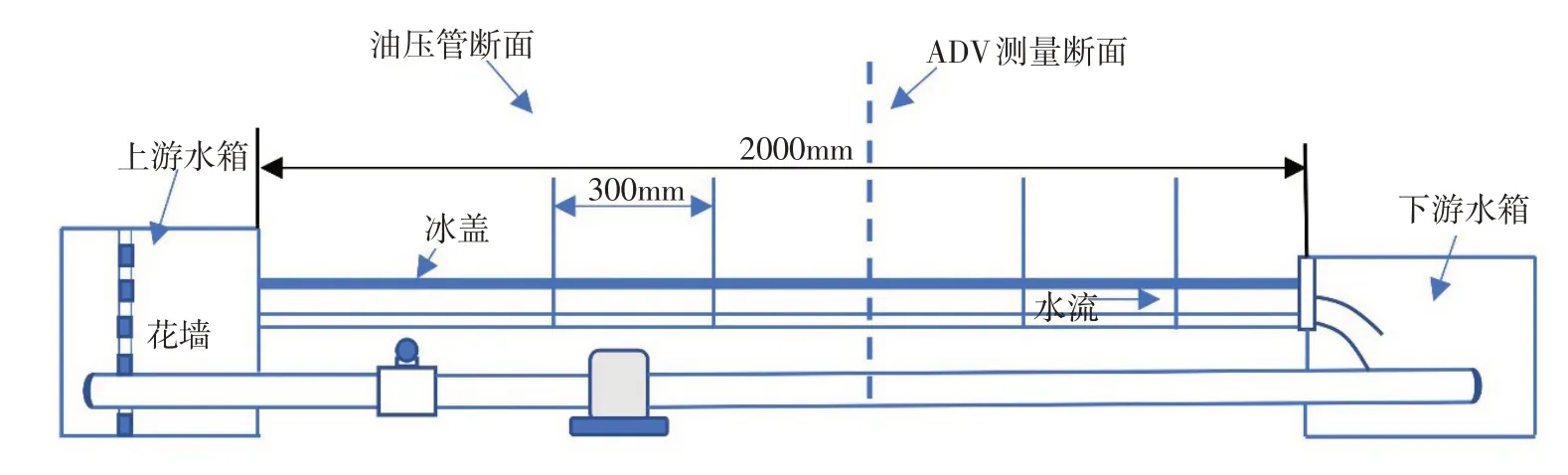
图2 实验装置的剖面
实验采用多普勒超声测速仪(ADV)对过流断面的流速进行点测,每点流速采集30 s,共600组数据再用origin软件进行后处理得到可信的沿水深方向的流速分布。在测量过程中发现水泵会对多普勒超声三位测速仪的测量结果产生一定的影响,为此须将测点安置在尽量远离水泵的位置。
试验工况选择了表1所示的两种进流量。稳定流量冰盖下复式断面水流的流态均为恒定流。模型参数以及糙率的率定采用漫滩水深为6 cm和8 cm的工况。在表2中给出了模型试验中复式断面渠道的模型参数。其中:Q为流量;底坡S0由渠道进出口的高程差值计算得到,过流断面形状对糙率有不可忽视的影响。
当求解得到冰盖下复式断面河道的水深平均流速沿横向y的分布时,如表4,为实测的半宽断面各断面平均流速,由式(8)可以计算出断面流量Qd。当冰盖糙率系数[17]通过率定得到ni=0.025,认为冰盖厚度是均匀的,则求解两种工况可得流量Qd,列于表5。

表4 实测各断面平均速度 (单位:m/s)

表5 冰盖下复式断面的计算流量
观察表5可以看出,对于床面存在直角突变的冰盖下复式断面渠道,在两种不同水深下,实测流量与采用本文准二维模型计算的流量Qd非常接近,误差相对值一般小于5%,这表明本文的模型具有足够的计算精度,同时采用明渠的二次流系数和无因次涡流黏度的造成的误差是可以允许的。如图3为冰盖下典型复式断面渠道的主槽区和漫滩区典型断面的垂向流速分布图。(具体的断面位置在整个横断面的位置分布见图1。)由于模型冰盖的糙率大于床面的糙率,故沿水深方向的最大速度的位置离冰盖更近。其中图3(d)所示为滩槽交界处的流速分布,尤其在床面突变处,即7 cm深度附近的位置,其流速分布变得紊乱。图3(a)所示为靠近渠道边壁的测量断面,受到边壁的影响,其流速明显相比于漫滩区断面3较小,其流速分布也表现的没有规律性。
图4 展示了在冰封条件下,水深的平均流速Ud与横坐标y的关系曲线。由于渠道和冰盖以及入流条件的对称性,其流动也是对称的,其位于主槽区的中心线处的流速梯度应当为零,即需满足边界条件当y=0 时,∂Ud∂y=0。所以对于全断面渠道可以由对称性求得。图5 利用ADV 在y向的速度分量绘制了横向速度矢量分布图。表明了二次流会从主槽区流向漫滩区;解释了动量从主槽区向漫滩区输移的现象;Ud计算值在交汇处的略大于流速实测值,而漫滩区的计算值略低于实测值。
4 结论
本文基于杨开林的冰盖下复式断面水深平均流速Ud的横向分布准二维模型,给出了顺直河道冰盖下复式断面漫滩水流准二维解析解。此外对于冰盖河渠的水流的无因次涡流黏度λ,可以采用明流无因次涡流黏度近似;通过物理模型实验验证了冰盖下复式断面漫滩水流沿水深的平均流速的横向分布准二维模型的合理性,并给出了典型断面的垂向流速分布图,通过横向流速矢量分布分析了计算值与实测值的误差产生的原因。即细微的误差主要是由于滩槽交界处存在二次流及动量交换而引起的;准二维模型计算的流量Qd与模型试验实测流量之间的误差相对值小于5%,具有令人满意的精度。
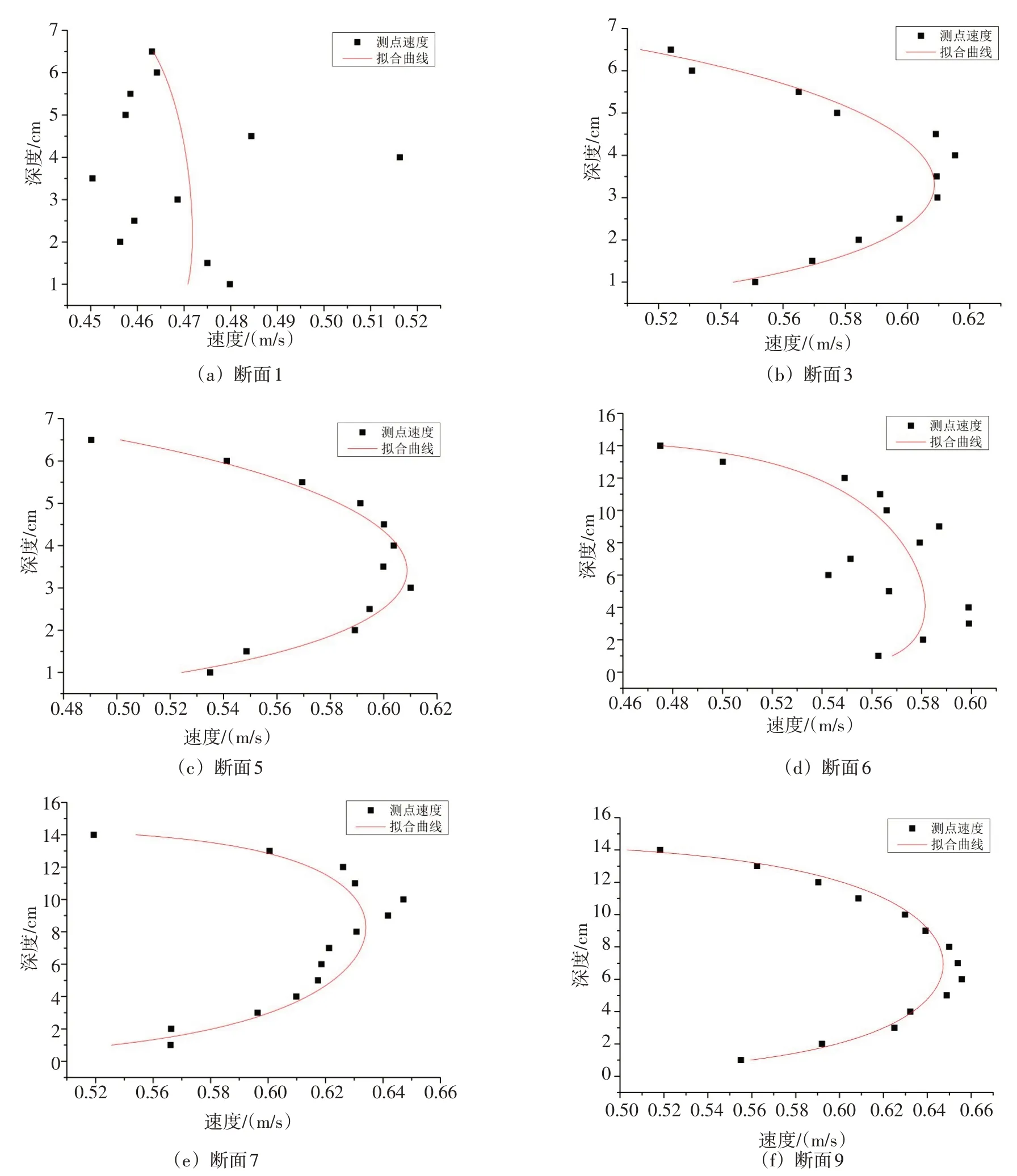
图3 8cm漫滩水深工况典型断面垂向流速分布
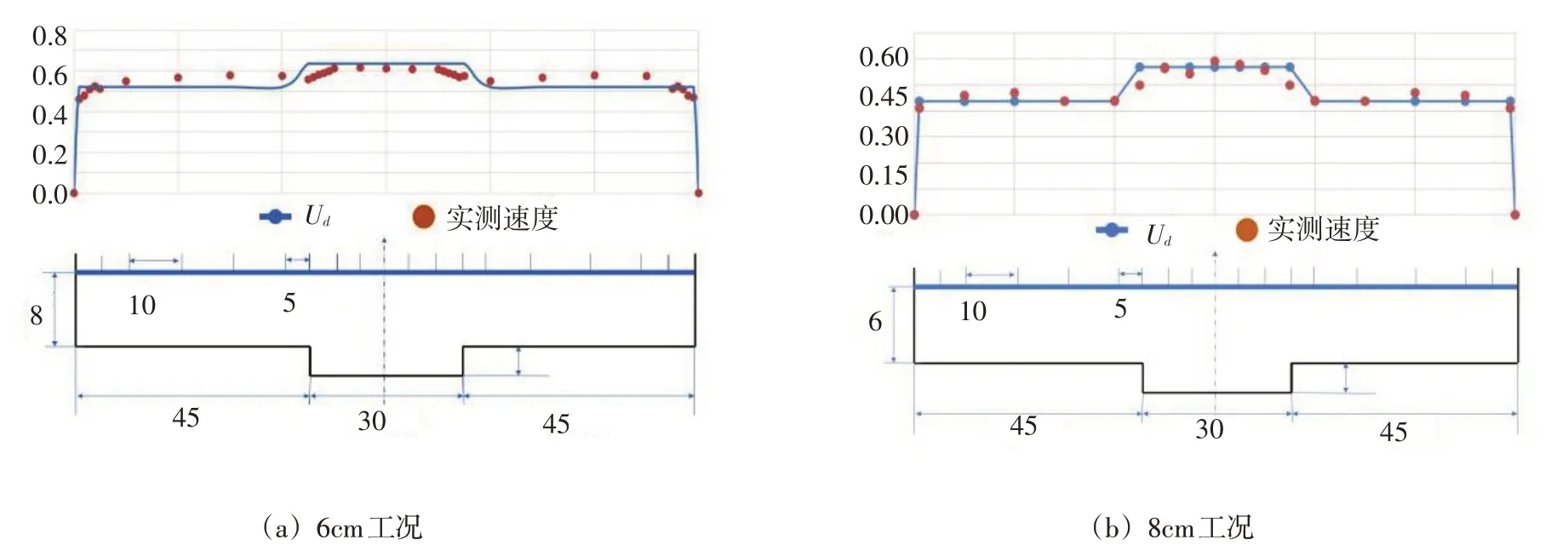
图4 实测速度对比
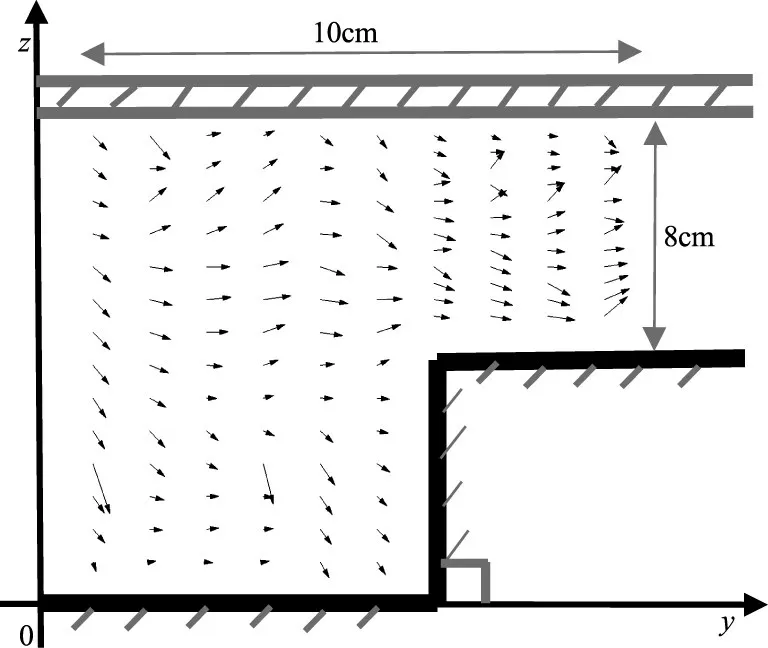
图5 典型复式断面冰盖下滩槽交汇区流速矢量分布
致谢:本文承中国水利水电科学研究院水力学研究所水力控制研究室提供试验条件,承王涛和郭新蕾两位教授级高级工程师的指导和帮助,特此表示感谢!
