基于正交实验和数据驱动的喷丸表面完整性参数预测

吴少杰，刘怀举，张仁华，张秀华，葛一波

表面强化技术

基于正交实验和数据驱动的喷丸表面完整性参数预测

吴少杰1，刘怀举1，张仁华1，张秀华1，葛一波2

（1.重庆大学 机械传动国家重点实验室，重庆 400044；2.上海恩太设备技术有限公司，上海 201806）

探究喷丸工艺参数对18CrNiMo7-6滚子表面完整性的影响规律，得到喷丸工艺参数与表面完整性的映射关系，提高喷丸工艺的质量与效率。运用Python语言对Abaqus进行二次开发，建立喷丸仿真的随机多弹丸模型并进行了试验验证。设计正交实验研究喷射角度、喷射速度、弹丸直径、覆盖率及弹丸类型对残余应力与表面粗糙度的影响规律，并用随机森林算法得到各个工艺参数对喷丸综合效果的重要度值。以喷射角度、喷射速度、弹丸直径、覆盖率、弹丸类型、距表面深度为输入，残余应力和表面粗糙度为输出，建立基于神经网络的喷丸表面完整性参数预测模型。通过正交实验分析得到弹丸直径和喷射速度对表面粗糙度有显著影响。各个喷丸工艺参数对18CrNiMo7-6滚子的喷丸综合效果的重要度依次为：喷射角度0.249，喷射速度0.224，弹丸类型0.193，覆盖率0.173，弹丸直径0.161。在各个工艺参数范围内，较优的工艺参数组合为：喷射角度90°，喷射速度80 m/s，弹丸直径0.7 mm，覆盖率300%，弹丸材料为铸钢丸。基于神经网络的喷丸表面完整性参数预测模型的平均相对误差低于7%。基于神经网络的喷丸表面完整性参数预测模型可以较准确地表示喷丸工艺参数与表面完整性参数之间的映射关系，能够为喷丸工艺提供相关参考。

喷丸强化；残余应力；表面粗糙度；正交实验；数据驱动；有限元仿真

随着航空航天、风电、船舶、高铁等重大装备向着长寿命、高可靠性方向发展，对以齿轮为代表的关键零部件表面质量提出更高的要求。喷丸作为一种表面强化技术，具有强化效果显著、适应面广、能耗低等特点，广泛应用于齿轮等重要零部件的表面强化。喷丸强化是一种金属表面冷加工工艺，其原理为高速喷射的丸流撞击金属零件表面，使其产生塑性变形，从而在零件表层引入残余压应力并改善表层组织结构，使零件产生组织强化和应力强化，提高零件的抗疲劳性能[1-3]。

国内外学者为探究喷丸工艺参数与表面完整性参数间的关联规律进行了大量的试验与仿真研究。许科飞等[4]研究了不同喷丸工艺参数对齿轮表面完整性的影响，发现提高喷丸覆盖率可以降低表面粗糙度及提高齿根表面的残余压应力。Nordin等[5]研究了喷丸工艺参数对表面硬化齿轮钢表面粗糙度的影响，在给定喷丸强度下，随着覆盖率的增大，表面粗糙度会增加，达到一定覆盖率后，粗糙度随覆盖率的增加而减小。Seki等[6]研究发现喷丸处理提高了齿轮的硬度、残余压应力及表面耐久性。Iida等[7]对比了钢丸和玻璃丸的喷丸效果，得出使用铸钢丸可以得到更大的表面残余压应力和表面硬度。Unal等[8]研究剧烈喷丸对AISI 1017钢的影响，得出表面硬度随喷丸强度的降低而减小，且在200 μm后，剧烈喷丸的效果消失。何嘉禧等[9]通过数值模拟研究了喷射速度、弹丸直径及覆盖率对二次喷丸后的残余应力、表面粗糙度的影响，发现提高二次喷丸的覆盖率可显著降低表面粗糙度。Wu等[10]通过实验与仿真研究覆盖率对残余应力及表面粗糙度的影响，实测残余应力和表面粗糙度与有限元仿真的误差在18%以内。Lin等[11]建立了一个包含位错密度本构方程的随机多弹丸模型，研究喷射速度、覆盖率及二次喷丸对残余应力、表面粗糙度和位错胞尺寸的影响。在实际喷丸过程中，影响残余应力、表面粗糙度等表面完整性参数的工艺参数众多，表面完整性参数与喷丸工艺参数间存在复杂的非线性关系，喷丸试验费时费力，喷丸工艺参数选取依赖经验。因此，需要探究喷丸工艺参数与表面完整性参数间的对应关系，以指导喷丸工艺。

为了探究喷丸工艺参数与表面完整性参数间的对应关系，实现表面完整性参数的预测，Miao等[12]基于Hertz理论、Zarka弹塑性理论，采用解析法得到喷射速度、弹丸直径与Almen强度的关系式，并对残余应力进行预测。李金魁等[13]通过引入无量纲弹痕直径参数，推导残余压应力场与无量纲弹痕直径的关系式，实现了不同材料的残余应力预测。陈家伟 等[14]基于有限元仿真和响应面法，得到铝合金的表面残余应力和变形与喷丸工艺参数间的对应关系。这种基于物理模型的表面完整性预测公式繁琐，试验复杂且工作量大。而基于神经网络的数据驱动方法无需知道喷丸具体作用机理，根据已有的喷丸工艺数据进行学习，可以对表面完整性参数进行预测，已被广泛用于机械零部件的寿命预测[15-16]、故障诊断[17]研究。目前采用神经网络研究喷丸工艺参数对表面完整性参数影响规律的研究较少。本文运用Python语言对Abaqus进行二次开发，建立喷丸仿真的随机多弹丸模型并进行了试验验证，设计正交实验进行有限元仿真，研究喷射角度、喷射速度、弹丸直径、覆盖率、弹丸类型对18CrNiMo7-6滚子的喷丸综合效果的影响；建立基于神经网络的喷丸表面完整性参数预测模型，探究喷丸工艺参数与表面完整性参数间的映射关系，实现表面完整性参数的快速预测，提高喷丸的质量与效率，为喷丸工艺人员提供相关参考。

1 研究方法

1.1 正交实验设计

正交实验是目前常用的试验优化分析方法[18]，利用标准化正交表安排喷丸工艺方案，对表面完整性参数结果进行极差分析，得出较优喷丸工艺参数组合。喷丸强度作为评价喷丸效果的一个重要指标，其大小直接影响残余压应力场、表面粗糙度等表面完整性参数，进而影响零部件的疲劳性能。在实际喷丸工艺中，铸钢丸与钢丝切丸常用于齿轮等零部件的喷丸处理，喷丸强度与喷射速度呈线性关系[19]。喷丸覆盖率[20]是指喷丸后零件表面凹坑面积占总面积的百分比。通过阿夫拉米公式[21]计算特定覆盖率下所需的弹丸数量，如公式（1）所示。其中，为覆盖率，表示弹痕半径（mm），为弹丸数量。

本文选取弹丸直径（）、喷射角度（）、喷射速度（）、覆盖率（）、弹丸类型（M）5个因素。其中，弹丸直径为4水平，取值为0.5、0.6、0.7、0.8 mm；喷射角度为4水平，取值为45°、60°、 75°、90°；喷射速度为4水平，取值为60、80、100、120 m/s[22]；覆盖率为3水平，取值为100%、200%、300%[23]；弹丸类型为3水平，取为铸钢丸（ZG）、钢丝切丸（CW）、高硬度钢丝切丸（HCW）。由于本喷丸工艺试验各因素的水平数不相等，为混合水平的多因素试验，采用拟水平法进行处理[24]。将覆盖率的水平4用水平1替换，弹丸类型的水平4用水平1替换。喷丸工艺正交实验因素水平如表1所示。

表1 喷丸工艺正交实验因素水平

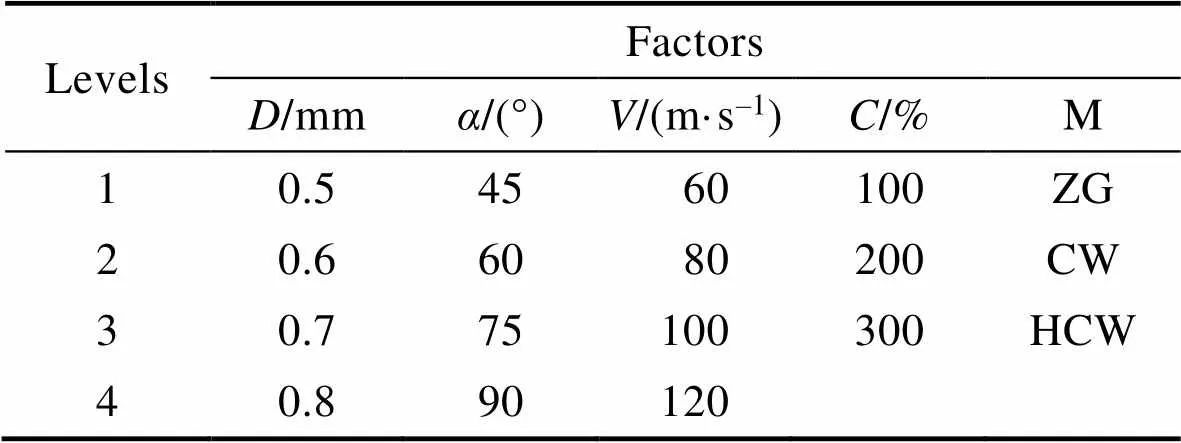
Tab.1 Orthogonal experimental factor levels for shot peening process

确定好喷丸工艺正交实验的因素和水平数之后，利用统计分析软件Minitab进行混合水平的多因素实验设计。为了弹丸类型表示方便，将铸钢丸用1表示，钢丝切丸用2表示，高硬度钢丝切丸用3表示，最终的喷丸工艺正交实验方案如表2所示。

表2 喷丸工艺正交实验方案

Tab.2 Orthogonal experiment scheme of shot peening process

1.2 随机多弹丸喷丸有限元模型

在有限元商业软件Abaqus中建立一长宽高分别为5 mm×5 mm×5 mm的小方块来模拟18CrNiMo7-6滚子的喷丸过程。在喷丸强化过程中，在弹丸的撞击下，靶体表层发生弹塑性变形，靶体选用随动强化本构模型[23]；铸钢丸、钢丝切丸、高硬度钢丝切丸的本构模型均为各向同性，弹丸和靶体的力学性能参数如表3所示。为了减少计算量，在小方块的中心位置分割一个1 mm×1 mm×1 mm的正方体来作为喷丸区域，并加密网格，保证模型的计算精度。为减小模型边界上的应力波反射对仿真结果造成的影响，把模型边界处单元类型设置为无限单元（CIN3D8）。模型喷丸区域单元类型为C3D8R，模型喷丸区域与边界的过渡区域单元类型为C3D8R，喷丸区域网格大小为20 μm。弹丸与靶体之间的切向摩擦设置为罚函数（penalty），摩擦系数为0.2[25]，法向行为设置为“硬接触”[26]。模型建立好后，选用ABAQUS/Explicit求解器的显示时间积分算法进行求解，建立的随机多弹丸有限元模型如图1所示。

为了验证随机多弹丸喷丸有限元模型的正确性，采用气动式喷丸机（Peentech，MT25-G80IIE/1/R）对18CrNiMo7-6材料制造的滚子进行喷丸试验。弹丸采用直径为0.6 mm的钢丝切丸，其硬度为55~62HRC，气压为0.5 MPa，喷嘴距待喷试件表面200 mm，喷枪移动速度为167.8 mm/min，喷丸流量为8 kg/min，喷射角度为90°，覆盖率为200%。由于在喷丸过程中喷丸速度不能直接测量，喷丸速度通过气压、喷丸流量、弹丸直径之间的公式（2）[28]计算得到。在上述工艺参数下，通过公式（2）计算的速度为56.4 m/s。

表3 弹丸和靶体的力学性能参数

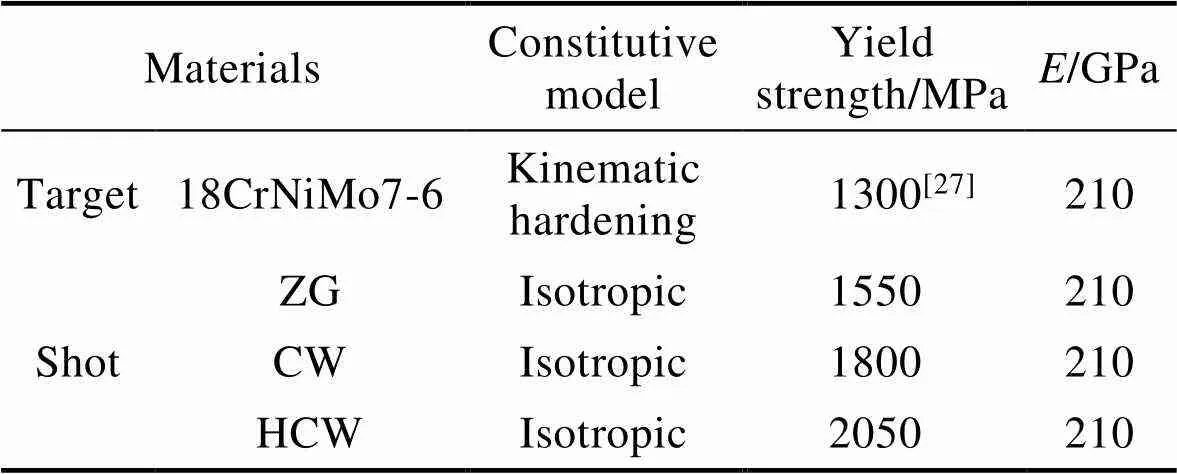
Tab.3 Mechanical property parameters of shot and target

图1 随机多弹丸有限元模型

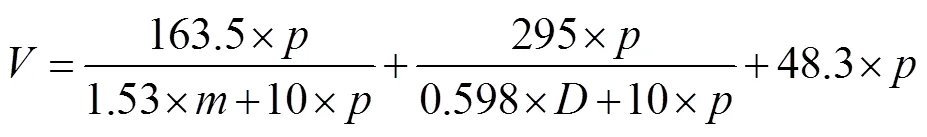
采用LXRD型X射线应力测试仪（Cr靶，衍射角2为156.3°，电压为30 kV，电流为25 mA）测量残余应力，如图2所示。用饱和食盐水对试件进行电解抛光，完成沿深度方向的残余应力测量。一般残余压应力影响层深约为0.15~0.3 mm[29]，故取0~0.25 mm深度下的残余应力值。测量的残余应力结果与仿真值对比如图3所示。可以看出，试验的表面残余压应力值、最大残余压应力值分别为–706、–1078 MPa；随机多弹丸有限元模型仿真的表面残余压应力值、最大残余压应力值分别为–609、–1020 MPa；相对误差分别为13.7%、5.4%。有限元仿真值与试验值吻合较好，可以验证随机多弹丸喷丸有限元模型的正确性。

采用多功能摩擦磨损试验台（RTEC MFT-5000）中的表面形貌测量模块（白光干涉仪）对上述喷丸后滚子的表面粗糙度进行测量，以进一步验证随机多弹丸有限元模型的正确性。在测量过程中，选用10×的放大倍数进行观察和测量。由于所测量滚子的几何形状是弧形，为了消除宏观曲率半径的影响，对初始测量的表面形貌数据进行处理，以获得平整的表面形貌数据，测量的三维表面形貌如图4所示。试验测量的表面粗糙度值为2.04 μm，随机多弹丸有限元仿真的表面粗糙度值为2.30 μm，表面粗糙度仿真值与试验值的误差小于0.3 μm，仿真值与试验值吻合较好。

图2 残余应力测试

图3 残余应力仿真值与试验值对比

1.3 喷丸性能预测的GA-BP神经网络模型

本文以弹丸直径、覆盖率、喷射速度、喷射角度、弹丸类型和距表面深度为模型的输入参数，残余应力及表面粗糙度为输出参数，则模型的输入层节点数为6，输出层节点数为2，神经网络的隐藏层取2[30]，将有限元仿真所得到的数据按照3∶1的比例随机划分为训练集和测试集。喷丸表面完整性参数预测的神经网络结构拓扑图如图5所示。

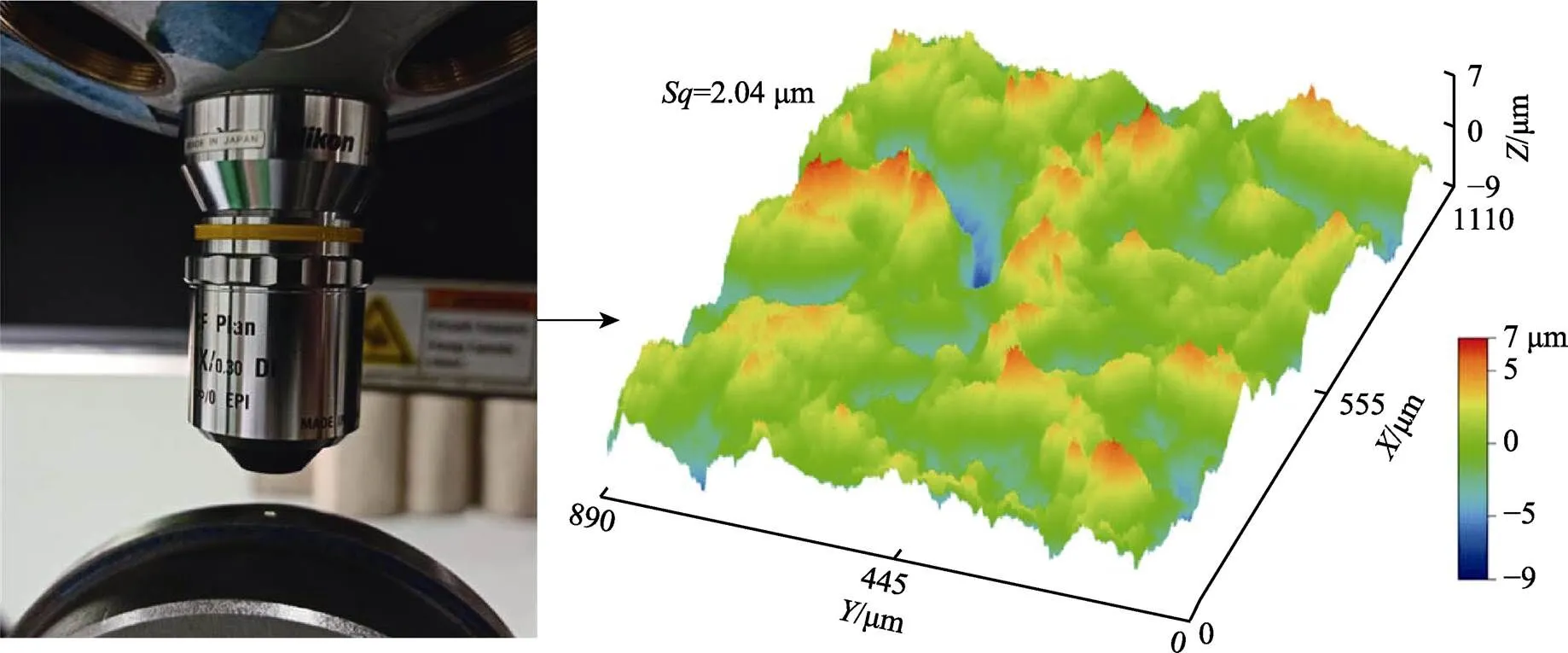
图4 表面形貌测量结果

图5 喷丸性能预测的GA-BP神经网络结构图

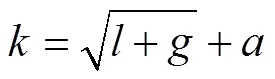
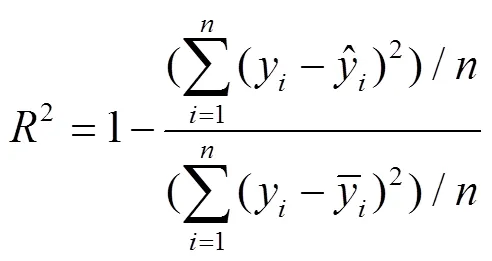
采用遗传算法（Genetic Algorithms，GA）[32]对喷丸强化性能预测的BP神经网络模型初始权值和偏置进行优化，以残余应力、表面粗糙度的预测值和实际值之间的误差平方和的倒数作为适应度函数，如公式（7）所示。采用实数编码的方法对待优化的参数进行编码，编码完成后，经选择、交叉、变异寻找出最优数值，建立基于GA-BP神经网络的喷丸表面完整性参数预测模型。

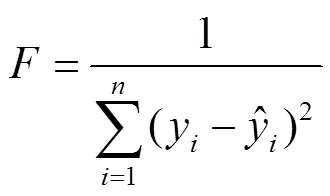
2 结果及分析

2.1 喷丸仿真正交实验结果

本文研究喷射角度、喷射速度、弹丸直径、覆盖率、弹丸类型对喷丸综合效果的影响，有限元计算完成后的残余应力云图如图6所示。可以看出，第4、8、12、16组的最大残余应力分别为–1621、–1685、–1834、–1751 MPa，表面局部位置出现残余拉应力，残余压应力分布不均匀，残余应力沿深度方向有明显的变化趋势。

然后以平均应力法[20]求出残余应力沿深度方向的残余应力曲线，将每层表面节点的应力值取平均值作为该层的残余应力值，以0.02 mm为一层，得到的残余应力曲线如图7所示。可以看出，从表面到0.1~0.2 mm的深度下，残余压应力逐渐增加到最大值，且随着深度的增加，残余压应力逐渐增大，到0.25~0.35 mm深度位置，残余压应力消失并逐渐转变为残余拉应力，表层的残余压应力值为–459~–583 MPa，最大残余压应力为–919~–1022 MPa，弹丸直径、喷射速度、覆盖率和弹丸材料4个工艺参数一同影响着残余应力结果。

图6 4、8、12、16组残余应力云图

图7 4、8、12、16组残余应力曲线

提取喷丸区域的表面位移，采用三维表面粗糙度均方根偏差来作为表面粗糙度评价参数[33]。是衡量三维表面粗糙度的重要参数之一，计算式见式（8），其中为节点数目，Z为随机多弹丸喷丸有限元模型向变形后的坐标位移。接触表面微观形貌可能利于润滑油的存储，但粗糙度过大会导致局部应力集中，从而影响表层和次表层材料的疲劳寿命[34]。

提取的表面粗糙度数据如图8所示。其中第13组工艺参数为弹丸直径0.8 mm、喷射角度45°、喷射速度120 m/s、覆盖率200%、弹丸材料为高硬度钢丝切丸，表面粗糙度达到最大，为4.71 μm；第1组工艺参数为弹丸直径0.5 mm、喷射角度45°、喷射速度60 m/s、覆盖率100 %、弹丸材料为铸钢丸，表面粗糙度最小，为1.4 μm。可以看出，随着弹丸直径从0.5 mm变化到0.8 mm，喷丸速度从60 m/s增加到120 m/s，表面粗糙度从1.4 μm增加到4.71 μm，增加了2.36倍。弹丸直径和喷射速度会显著影响工件表面粗糙度，在实际工件喷丸过程中，应选用较小的弹丸直径和喷射速度，以获得较小的表面粗糙度，提高齿轮等零部件的疲劳寿命。

图8 表面粗糙度Sq仿真值

在喷丸工艺中，表面残余压应力（srcs）、最大残余压应力（mcrs）、最大残余压应力深度（m）、残余压应力层深度（0）是工程中广泛被关注的参数，可以预估喷丸效果[35]。表层和次表层的残余压应力可以抵消齿轮等零部件工作时由负载引起的拉应力，同时可以抑制疲劳裂纹的萌生和扩展[36]。表面粗糙度是影响齿轮润滑、服役性能的重要参数，表面粗糙度过大导致应力集中，影响表层或次表层零件的疲劳寿命[37]。为评价各个工艺参数对喷丸综合效果的影响，采用百分制加权综合评分法[38]，如公式（9）所示，将表面粗糙度、表面残余压应力、最大残余压应力、残余压应力层深度、最大残余压应力深度5个参数进行归一化，根据工程经验及5个参数对喷丸综合效果的影响，分配给表面粗糙度、表面残余压应力、最大残余压应力、残余压应力层深度、最大残余压应力深度的权重分别为40%、20%、20%、10%、10%，计算的综合评分如表4所示。其中，为加权后的综合评分，b为各个参数的权重，Y为每个参数归一化后的值，=1,2,3,4,5。

表4 喷丸工艺正交实验结果

Tab.4 Orthogonal experiment results of shot peening process

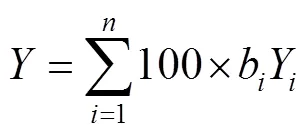
在喷丸工艺参数的极差分析中，极差越大，表示该工艺参数对喷丸综合效果的影响越显著。极差分析的结果如表5所示。可以看出，各个喷丸工艺参数对18CrNiMo7-6滚子的综合喷丸效果重要度依次为喷射角度、喷射速度、弹丸类型、覆盖率、弹丸直径，在各个工艺参数范围内，较优的工艺参数组合为：喷射角度90°，喷射速度80 m/s，弹丸直径0.7 mm，覆盖率300%，弹丸类型为铸钢丸。为了进一步量化各个工艺参数对喷丸综合效果的重要度，采用随机森林算法对工艺参数重要度进行评价。随机森林（Random Forest，RF）是以决策树为基学习器的集成学习算法，具有预测准确率高、泛化能力强的优点，可用于分类和回归分析，同时给出特征的重要度[40]。随机森林根据平均基尼指数（Mean Decrease Gini，MDG）和平均下降精度（Mean Decrease Accuracy，MDA）两种算法对喷丸工艺参数的重要度进行评价。由于随机森林的双重随机机制，仅使用属性在随机森林决策树中的出现频率来体现特征重要性不可取[41]，导致基于平均基尼指数的重要度分析方法精度较差。为了评价不同工艺参数对喷丸综合效果的重要度，本文选用平均下降精度进行特征重要性分析，重要性评分（Variable Importance Measure，VIM）公式如式（11）所示。

表5 喷丸综合评分结果极差分析

Tab.5 Range analysis of shot peening comprehensive score results

2.2 喷丸强化GA-BP神经网络预测结果

隐藏层神经元节点个数对喷丸表面完整性参数预测模型的精度影响显著。根据公式（3）初步确定隐藏层节点数范围为4~12，以决定系数²为精度评价参数，运用试错法得到喷丸表面完整性预测模型的精度随隐藏层节点数的变化曲线，如图9所示。可以看出，当节点数为4~6时，决定系数2随着节点数的增加而增大，当节点数为6时，2最大，为0.9978，当节点数为7~12时，2逐渐减小，随后稳定在0.91左右。

由表2正交实验方案共得到16组残余应力曲线，其中试验组数为2、8、11、15组的数据为测试集。

图10a为第2组残余应力有限元仿真值与神经网络预测值拟合图。图10b为有限元仿真值与神经网络预测值的对比图。可以看出，残余应力有限元仿真值与神经网络预测值吻合较好。

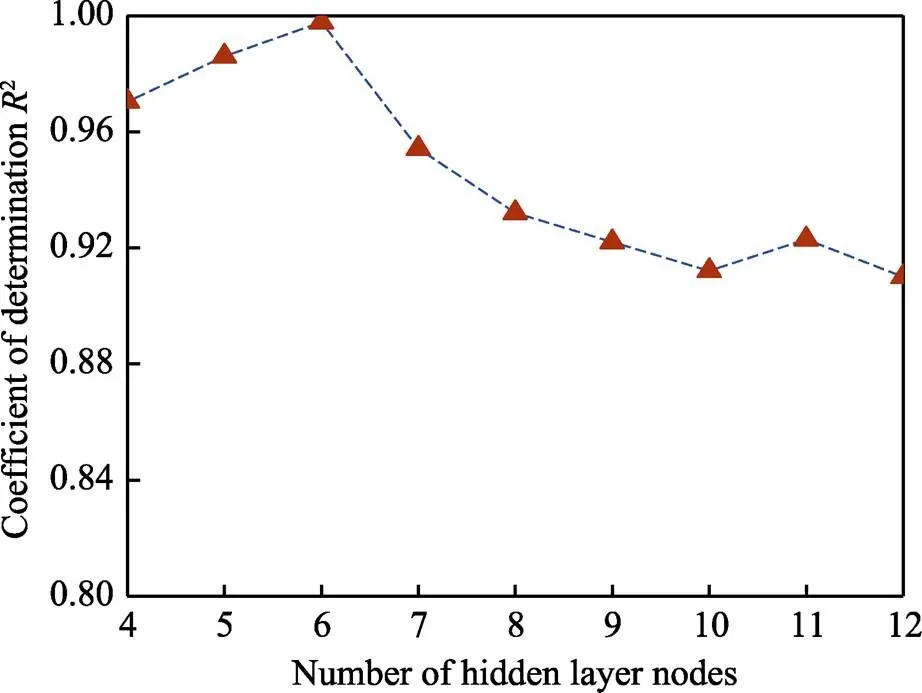
图9 喷丸性能预测模型R2随隐藏层节点数的变化

图10 第2组测试集残余应力神经网络预测值与有限元仿真值对比

计算了第2、8、11、15组测试集的表面残余压应力、最大残余压应力、残余压应力层深、最大残余压应力层深和表面粗糙度5个喷丸主要评价参数的神经网络预测值与有限元仿真值的相对误差，结果如图11所示。可以看出，最大残余压应力的相对误差为0.41%~2.29%，测试集中最大相对误差小于7%，预测结果的精度在喷丸工艺的可接受范围内。

喷丸表面完整性参数预测模型的精度评价参数有2、RMSE、MRE，以2为主要评价参数，预测模型精度评价如表6所示。可以看出，4组测试集的残余应力决定系数（2）均大于0.99，平均相对误差（MRE）均低于7%，其中第8组的预测精度最高，2为0.9967。采用4组测试集来验证模型精度，说明预测模型的泛化能力及鲁棒性，且在喷丸领域，此精度满足工程需求，可以为喷丸工艺人员提供相关参考。

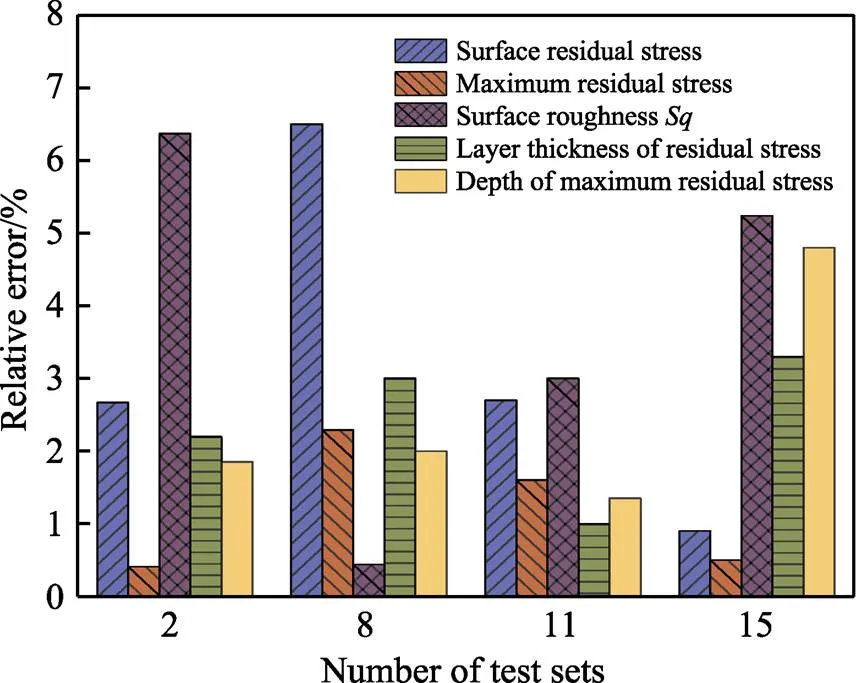
图11 测试集神经网络预测值与有限元仿真值的相对误差

表6 测试集的2、RMSE、MRE值

Tab.6 R2, RMSE and MRE values of the test sets

3 结论

1）喷丸各个工艺参数对18CrNiMo7-6滚子的综合喷丸效果的重要度依次为喷射角度（0.249）、喷射速度（0.224）、弹丸类型（0.193）、覆盖率（0.173）、弹丸直径（0.161）。在各个工艺参数范围内，较优的工艺参数组合为：喷射角度90°，喷射速度80 m/s，弹丸直径0.7 mm，覆盖率为300%，弹丸材料为铸钢丸。

2）基于GA-BP神经网络的喷丸表面完整性参数预测模型，残余应力的决定系数²大于0.99，残余应力和表面粗糙度的平均相对误差均低于7%，此模型可以较准确地表示喷丸工艺参数与表面完整性参数之间的映射关系，预测精度满足工程需求。

[1] TEKELI S. Enhancement of fatigue strength of SAE 9245 steel by shot peening[J]. Materials letters, 2002, 57(3): 604-608.

[2] TORRES M A S, VOORWALD H J C. An evaluation of shot peening, residual stress and stress relaxation on the fatigue life of AISI 4340 steel[J]. International journal of fatigue, 2002, 24(8): 877-886.

[3] 李行, 张继旺, 易科尖, 等. 喷丸处理EA4T车轴钢疲劳性能和残余应力松弛行为研究[J]. 表面技术, 2019, 48(10): 244-250.LI Xing, ZHANG Ji-wang, YI Ke-jian, et al. Fatigue pro­perties and residual stress relaxation behavior of shot pee­ned EA4T axle steel[J]. Surface technology, 2019, 48(10): 244-250.

[4] 徐科飞. 喷丸工艺对18CrNiMo7-6齿轮弯曲疲劳强度的影响研究[D]. 郑州: 郑州大学, 2016.XU Ke-fei. Study on effect of shot peening on bending fatigue strength of 18CrNiMo7-6 gear[D]. Zhengzhou:Zhengzhou University, 2016.

[5] NORDIN E, ALFREDSSON B. Experimental investiga­tion of shot peening on case hardened SS2506 gear steel [J]. Experimental techniques, 2017, 41(4): 433-451.

[6] SEKI M, YOSHIDA A, OHUE Y, et al. Influence of shot peening on surface durability of case-hardened steel gears [J]. Journal of advanced mechanical design systems and manufacturing, 2007, 1(4): 518-529.

[7] IIDA K, TOSHA K. Comparison between steel shot and glass shot on the peened surface and the surface layer[J]. Journal of the Japan Society for Precision Engineering, 1988, 54(5): 922-927.

[8] UNAL O, VAROL R. Almen intensity effect on microstr­u­cture and mechanical properties of low carbon steel sub­jected to severe shot peening[J]. Applied surface science, 2014, 290: 40-47.

[9] 何嘉禧, 汪舟, 甘进, 等. 二次喷丸42CrMo钢表面完整性的数值模拟研究[J]. 表面技术, 2020, 49(6): 216- 223. HE Jia-xi, WANG Zhou, GAN Jin, et al. Numerical simu­lation on surface integrity of 42CrMo steel after dual shot peening[J]. Surface technology, 2020, 49(6): 216-223.

[10] WU J Z, LIU H J, WEI P T, et al. Effect of shot peening coverage on residual stress and surface roughness of 18CrNiMo7-6 steel[J]. International journal of mechani­cal sciences, 2020, 183: 105785.

[11] LIN Q J, LIU H J, ZHU C C, et al. Effects of different shot peening parameters on residual stress, surface roug­hness and cell size[J]. Surface & coatings technology, 2020, 398: 126054.

[12] MIAO H Y, LAROSE S, PERRON C, et al. An analytical approach to relate shot peening parameters to almen int­ensity[J]. Surface & coatings technology, 2010, 205(7): 2055-2066.

[13] 李金魁, 姚枚, 王仁智. 度量喷丸强度的新参量[J]. 航空材料学报, 1989(4): 38-45.LI Jin-kui, YAO Mei, WANG Ren-zhi.A new parameter measuring shot peening intensity[J].Journal of aeronau­tical materials, 1989(4): 38-45.

[14] 陈家伟, 廖凯, 李立君, 等. 铝合金喷丸工艺参数-表面特征值的函数关系与应用[J]. 表面技术, 2019, 48(6): 212-220.CHEN Jia-wei, LIAO Kai, LI Li-jun, et al.Function rela­tionship between shot peening parameters and surface characteristic of Al-based alloy and application[J]. Sur­face technology, 2019, 48(6): 212-220.

[15] 裴洪, 胡昌华, 司小胜, 等. 基于机器学习的设备剩余寿命预测方法综述[J]. 机械工程学报, 2019, 55(8): 1-13. PEI Hong, HU Chang-hua, SI Xiao-sheng, et al. Review of machine learning based remaining useful life predic­tion methods for equipment[J]. Journal of mechanical eng­ineering, 2019, 55(8): 1-13.

[16] QIN Y, XIANG S, CHAI Y, et al. Macroscopic-microscopic attention in LSTM networks based on fusion features for gear remaining life prediction[J]. IEEE transactions on industrial electronics, 2020, 67(12): 10865-10875.

[17] 温江涛, 周熙楠. 模糊粒化非监督学习结合随机森林融合的旋转机械故障诊断[J]. 机械科学与技术, 2018, 37(11): 88-96. WEN Jiang-tao, ZHOU Xi-nan. Fault diagnosis of rotat­ing machinery in combination with unsupervised learning of fuzzy granulation and random forest fusion[J]. Mecha­nical science and technology for aerospace engineering, 2018, 37(11): 88-96.

[18] SINGH L, KHAN R A, AGGARWAL M L. Empirical modeling of shot peening parameters for welded auste­nitic stainless steel using grey relational analysis[J]. Jou­rnal of mechanical science & technology, 2012, 26(6): 1731-1739.

[19] KÖNITZER A M, POLANETZKI H. Implementation of velocity measurement as intensity verification in produc­tion[C]//International conference on shot peening (ISCP- 11). Indiana South Bend: Shotpeener, 2011: 11-17.

[20] BAGHERIFARD S, GHELICHI R, GUAGLIANO M. On the shot peening surface coverage and its assessment by means of finite element simulation: A critical review and some original developments[J]. Applied surface sci­ence, 2012, 259: 186-194.

[21] KIRK D. Shot peening[J]. Aircraft engineering & aeros­pace technology, 1999, 71(4): 349-361.

[22] NORDIN E, ALFREDSSON B. Measuring shot peening media velocity by indent size comparison[J]. Journal of materials processing technology, 2016, 235: 143-148.

[23] SEDDIK R, BAHLOUL A, ATIG A, et al. A simple meth­­odology to optimize shot-peening process parameters using finite element simulations[J]. International journal of adv­a­nced manufacturing technology, 2017, 90(5): 2345-2361.

[24] 杨德. 试验设计与分析[M]. 北京: 中国农业出版社, 2002: 194-196.YANG De.Design and analysis of experiments[M]. Beijing:Agricultural Press of China, 2002: 194-196.

[25] LIN Q J, LIU H J, ZHU C C, et al. Investigation on the effect of shot peening coverage on the surface integrity[J]. Applied surface science, 2019, 489: 66-72.

[26] 闫五柱, 张嘉振, 周振功. 喷丸过程中的摩擦影响研究[J]. 热加工工艺, 2014, 43(18): 134-136.YAN Wu-zhu, ZHAGN Jia-zhen, ZHOU Zhen-gong.Study on friction during shot peening process[J].Hot working technology, 2014, 43(18): 134-136.

[27] WANG W, LIU H J, ZHU C C, et al. Evaluation of roll­ing contact fatigue of a carburized wind turbine gear con­sidering the residual stress and hardness gradient[J]. Jour­nal of tribology-transactions of the ASME, 2018, 140: 0614016.

[28] XIE L C, ZHANG J, XIONG C B, et al. Investigation on experiments and numerical modelling of the residual stress distribution in deformed surface layer of Ti-6Al-4V after shot peening[J]. Materials and design, 2012, 41: 314-318.

[29] VAARA J, KUNNARI A, FRONDDELIUS T. Literature review of fatigue assessment methods in residual stressed state[J]. Engineering failure analysis, 2020, 110: 104379.

[30] KOHLI A, DIXIT U S. A neural-network-based methodo­logy for the prediction of surface roughness in a turning process[J]. International journal of advanced manufactur­ing technology, 2005, 25(1-2): 118-129.

[31] NAGELKERKE N J D. A note on a general definition of the coefficient of determination[J].Biometrika, 1991, 78(3): 691-692.

[32] 李文龙, 陈燕, 赵杨, 等. 采用神经网络和遗传算法优化磁粒研磨TC4弯管工艺参数[J]. 表面技术, 2020, 49(6): 330-336. LI Wen-long, CHEN Yan, ZHAO Yang, et al. Optimizing technological parameters of magnetite grinding TC4 elbow by neural network and genetic algorithms[J]. Surface tec­hnology, 2020, 49(6): 330-336.

[33] HU Z X, ZHU L, TENG J X, et al. Evaluation of three- dimensional surface roughness parameters based on digital image processing[J]. International journal of advanced manufacturing technology, 2009, 40(3-4): 342-348.

[34] ZHANG B Y, LIU H J, BAI H Y, et al. Ratchetting- multiaxial fatigue damage analysis in gear rolling contact considering tooth surface roughness[J]. Wear, 2019, 428- 429: 137-146.

[35] 朱鹏飞, 严宏志, 陈志, 等. 齿轮齿面喷丸强化研究现状与展望[J]. 表面技术, 2020, 49(4): 113-131.ZHU Peng-fei, YAN Hong-zhi, CHEN Zhi, et al. Research status and prospect of shot peening of gear tooth flanks[J]. Surface technology, 2020, 49(4): 113-131.

[36] 秦海迪, 张亚龙, 刘海鹏, 等. 喷丸对25CrNi2MoV钢滚动接触疲劳性能的影响[J]. 表面技术, 2020, 49(5): 222-229. QIN Hai-di, ZHANG Ya-long, LIU Hai-peng, et al. Effect of shot peening on rolling contact fatigue properties of 25CrNi2MoV steel[J]. Surface technology, 2020, 49(5): 222-229.

[37] 周文龙, 吕成, 李烨, 等. 喷丸强度对316不锈钢表面完整性及疲劳寿命的影响[J]. 表面技术, 2020, 49(7): 230-237. ZHOU Wen-long, LYU Cheng, LI Ye, et al. Effect of shot peening intensity on surface integrity and fatigue life of 316 stainless steel[J]. Surface technology, 2020, 49(7): 230-237.

[38] 王利平, 王建明, 赵莉莉. 基于正交试验法的喷丸工艺多目标参数优化[J]. 现代制造工程, 2016(3): 110-114. WANG Li-ping, WANG Jian-ming, ZHAO Li-li. Multi- object optimization for the shot peening parameters based on orthogonal experiment method[J]. Modern manufactu­r­ing engineering, 2016(3): 110-114.

[39] 侯化国, 王玉民. 正交试验法[M]. 长春: 吉林人民出版社, 1985: 74-76. HOU Hua-guo, WANG Yu-min.Orthogonal experiment [M]. Changchun:Jilin People’s Publishing House, 1985: 74-76.

[40] BREIMAN L. Random forests[J]. Machine learning, 2001, 45(1): 5-32.

[41] 黄梅, 朱焱. 基于随机森林特征重要性的-匿名特征优选[J]. 计算机应用与软件, 2020, 37(3): 266-270. HUANG Mei, ZHU Yan.-anonymity feature optimiz­a­tion based on the importance of random forest features[J].Computer applications and software, 2020, 37(3): 266-270.

Prediction of Surface Integrity Parameters of Shot Peening Based on Orthogonal Experiment and Data-driven

1,1,1,1,2

(1.State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China; 2.Shanghai Peentech Equipment Tech. Co. Ltd, Shanghai 201806, China)

This paper aims to study the influence of process parameters of shot peening on the surface integrity of 18CrNiMo7-6 roller and acquire the mapping relation between process parameters and surface integrity, so as to improve the quality and efficiency of shot peening process. During this, Python language was used for the secondary development of Abaqus to establish the random multi-shots model of shot peening simulation and the experimental verification was carried out. Orthogonal experiment was designed to study the effect laws of impact angle, impact velocity, shot diameter, coverage and shot type on residual stress and surface roughness, and the importance value of each process parameter on the comprehensive effect of shot peening was obtained by the random forest algorithm. With impact angle, impact velocity, shot diameter, coverage, shot type and surface depth as input values and residual stress and surface roughness as output values, a prediction model of shot peening surface integrity based on neural network was established. Through the orthogonal test, it is found that the shot diameter and impact velocity have a significant influence on the surface roughness. The importance of each shot peening process parameter to the comprehensive shot peening effect of 18CrNiMo7-6 roller is impact angle (0.249), impact velocity (0.224), shot type (0.193), coverage (0.173) and shot diameter (0.161). The optimal combination of process parameters within the range of each process parameter is that the impact angle is 90°, the impact velocity is 80 m/s, the shot diameter is 0.7 mm, the coverage is 300%, and the shot material is cast steel shot. The average relative error of the shot peening surface integrity prediction model based on neural network is less than 7%. Therefore, it is concluded that the shot peening surface integrity prediction model based on neural network can accurately represent the mapping relation between the shot peening process parameters and surface integrity parameters, thus providing relevant reference for shot peening process.

shot peening strengthening; residual stress; surface roughness; orthogonal experiment; data-driven; finite element simulation

2020-01-05；

2020-05-09

WU Shao-jie (1997—), Male, Master, Research focus: data-driven and shot peening.

刘怀举（1986—），男，博士，副教授，主要研究方向为机械传动智能设计与抗疲劳制造。邮箱：huaijuliu@cqu.edu.cn

Corresponding author：LIU Huai-ju (1986—), Male, Doctor, Associate professor, Research focus: intelligent design of mechanical transmission and anti-fatigue manufacture. E-mail: huaijuliu@cqu.edu.cn

吴少杰，刘怀举，张仁华, 等.基于正交实验和数据驱动的喷丸表面完整性参数预测[J]. 表面技术, 2021, 50(4): 86-95.

TG668

A

1001-3660(2021)04-0086-10

10.16490/j.cnki.issn.1001-3660.2021.04.008

2020-01-05；

2020-05-09

国家自然科学基金（51975063）；重庆市自然科学基金重点项目（cstc2019jcyj-zdxmX0007）

Fund：Supported by the National Natural Science Foundation of China (51975063), Key Program of Natural Science Foundation of Chongqing (cstc2019jcyj-zdxmX0007)

吴少杰（1997—），男，硕士研究生，主要研究方向为数据驱动与喷丸强化。

WU Shao-jie, LIU Huai-ju, ZHANG Ren-hua, et al. Prediction of surface integrity parameters of shot peening based on orthogonal experiment and data-driven[J]. Surface technology, 2021, 50(4): 86-95.