基于AFSA的高速无人艇操纵模型参数辨识

杨 鑫，邵 兴

（中国船舶重工集团有限公司第七一〇研究所，湖北 宜昌 443003）

0 引言

水面无人艇（unmanned surface vessel，USV），简称无人艇，是一种无人化的水面智能任务平台，具有体积小、性价比高、高速智能等优势，广泛应用于海洋环境监测、水文地理勘察、海上巡逻与搜救、军事侦察、反潜作战等领域，近年来备受各国研究人员关注[1-3]。随着船用发动机、艇型优化设计、推进技术等的提升，无人艇的设计航速也越来越高，相应的对其操纵性要求也越来越高[4-6]。通常为了对高速无人艇的操纵性进行准确的预报和评估，先要建立比较精确的操纵运动数学模型[7-8]，其中操纵响应模型结构相对简单，应用方便广泛，对其研究有重要意义。

无人艇操纵响应数学模型的建立，关键是如何确定数学模型中的各个参数。船舶操纵运动模型参数主要通过模型实验法、CFD仿真计算以及参数辨识法获得[9]，而参数辨识法较为实用有效。它将操纵运动船舶视为一个动态系统，通过试验测得系统输入（舵角、螺旋桨转速等控制量）和系统输出（船速、艏向角等运动量），再运用模型辨识方法，对模型中的参数进行求解。

当前，在国内外有部分学者采用一些传统辨识方法对船舶运动模型进行了求解。赵大明等人应用扩展卡尔曼滤波算法对船舶运动模型参数辨识，在辨识实验中，采用固定区间卡尔曼平滑算法进行数据预处理，使结果收敛性有一定提升[9]。Sutulo S等人基于经典的遗传算法，进行了操纵数学模型辨识[10]；上海交通大学的邹早建团队，应用支持向量回归机对船舶操纵运动响应模型进行了机理建模，同时进行改进，结合最小二乘法以及引入粒子群算法对惩罚因子 C值进行寻优，从核函数结构中得到了模型中的操纵性指数[11-13]。

总结分析发现，现有方法在参数辨识过程中，存在计算量大不适合在线辨识或者计算量小但泛化能力较差的问题。人工鱼群算法（AFSA）具有高效、智能寻优的特性，所以本文基于AFSA与模型试验相结合的方法，对高速无人艇的操纵响应模型进行辨识求解，在得到比较精确模型参数的同时也提升了效率。

1 高速无人艇操纵响应数学模型

无人艇操纵响应模型是船舶运动控制领域中应用最广泛的数学模型。目前对船舶响应模型参数辨识的研究，多数是针对比较简单的一阶线性响应模型，对于需要频繁操舵以及大舵角操纵运动，非线性模型更精确。常用的一阶线性响应模型如下：

式中：r表示艏向角速度；δ为舵角；K为舵效系数，K越大意味着产生的转艏推力越大，回转性越好；T表示应舵性和航向稳定性。

考虑到高速无人艇的运动复杂特性，一阶线性模型无法有效地描述相应的特性，因而本文对精度较高的一阶非线性响应模型中的各项参数进行辨识研究。高速无人艇的一阶非线性响应模型可描述如下：

式中：α为非线性项系数，其它变量与式（1）相同。

2 响应模型参数辨识

2.1 人工鱼群算法基本原理

人工鱼群算法，主要是基于人工鱼个体的觅食、聚群和追尾 3种行为进行寻优[14]。在 AFSA中，每条鱼的位置被看作是待优化问题的一个可行解，每个解都有一个由适应度函数评估的适应度值。可以针对不同的待优化问题，合理地选择不同的适应度函数。

在每次迭代中，人工鱼会通过觅食、聚群和追尾等行为来更新自己的位置状态，具体的行为描述如下。

1）觅食行为：地域每一个人工鱼，令其当前位置状态向量为Xi，而向量Xj是人工鱼在其视野范围内任意选择另一个状态，如果新状态的食物浓度Yj大于当前状态的食物浓度iY，说明得到的状态优于当前状态，则向新选择状态靠近一步；如果Yj小于iY则重新选取新状态进行比较，如果选择次数达到最大次数try_ number后，仍不满足移动条件，则随机移动一步。该过程如公式（3）所示：

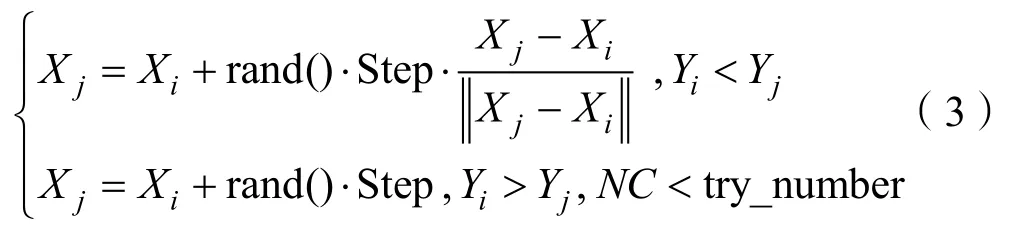
中心位置Xc的数学表达式为

向Xc移动的过程可由公式表示为

人工鱼向Xmax移动过程可由表达式（6）描述如下：

4）公告牌：记录人工鱼最优的状态。人工鱼获得新的状态后，与公告牌中记录的状态比较，若新获得的状态比公告牌中记录的状态更优秀，则替换掉公告牌中的状态；反之，则不变。

人工鱼群算法（AFSA）流程如图1所示。

图1 人工鱼群算法流程图Fig.1 Flow chart of AFSA

上述递推过程中，首先生成 m条人工鱼个体作为初始鱼群，在参数区间内为每个人工鱼随机初始化一个位置状态向量X，然后计算其追尾行为、聚群行为的适应度值Y，采用行为选择策略，选择最优的行为作为鱼的移动方向，缺省行为是觅食行为。计算出每条鱼的食物浓度函数值Y（目标函数），将最优值与公告板中的值进行比较，以完成对公告板上最优的值的实时更新。直到迭代次数达到N，最终公告板中的值就是最优值，对应的状态向量X即为最优解。

2.2 基于AFSA的构造辨识模型

对于无人艇操纵响应模型，先将模型进行离散化处理，并结合对应的优化方法构建相应的辨识模型，然后进行参数辨识。

通过前向差分法，将无人艇的一阶非线性响应模型进行离散化处理，对艏向角速度进行差分可得：

同理，对艏向角速度r的一阶导数r˙前向差分，可得：

将上述式（7）和式（8）代入一阶非线性响应模型式（2），得：

从而可将表达式（10）表示为

由此，将高速无人艇的一阶非线性响应模型转化成离散型系统，从而基于人工鱼群算法进行下一步求解。

基于AFSA能够对状态向量进行寻优的特性。将式（11）中λ的待辨识元素作为人工鱼的位置状态量X：

其中：

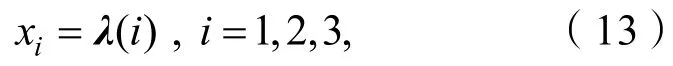
为了辨识得到对应参数值，此处确定适应度函数为

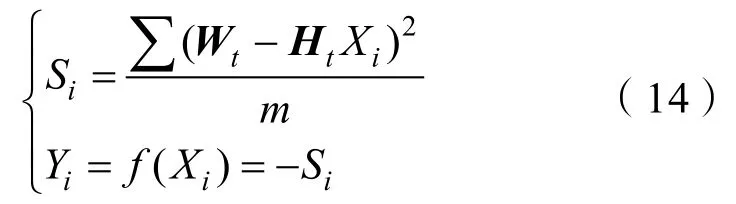
上述适应度函数即为计算样本的方差，其优化目标即为使得样本方差S最小。由此将基于人工鱼群算法来求解目标函数Y的最大值，即可得到方差S最小情况下的状态量X。

2.3 采集数据参数辨识

从文献[15]中选取1组一阶非线性响应模型参数，如表1所示。

表1 一阶非线性响应模型参数Table 1 Parameters of fist-order nonlinear response model

采用工程上广泛应用的四阶龙格-库塔法（Runge-Kutta）进行无人艇操纵运动的仿真预报：基于表1中的响应模型开展20°的Z形实验仿真，得到包括艏向角、舵角、角速度等数据的变化曲线如图2所示。

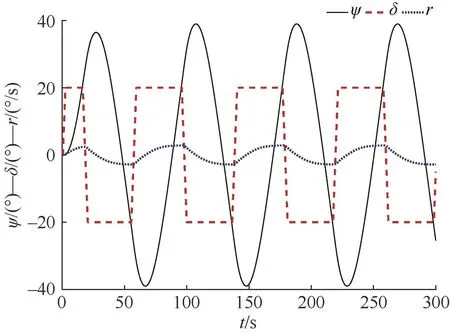
图2 20°Z形实验运动仿真结果Fig.2 Results of 20°Z test motion simulation

将图2中采集的仿真数据带入式（11）中的Wt和Ht，即可基于AFSA对系统状态向量X进行状态估计。其中，人工鱼群数量m=100，最大迭代次数N=50，拥挤度因子δ=0.618。

最后，得到适应度函数优化值随迭代次数变化情况，如图3所示。

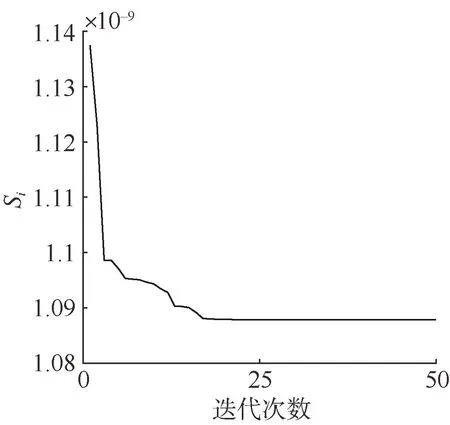
图3 适应度函数优化结果Fig.3 Optimal result of fitness function

同时，得到状态向量X中x1～x3的状态估计值，其辨识结果如图4-6所示。

图4 x1的辨识结果Fig.4 Identification result ofx1

图5 x2的辨识结果Fig.5 Identification result ofx2

图6 x3的辨识结果Fig.6 Identification result ofx3

x1～x3的最终辨识结果如表2所示。

表2 x1～x3辨识结果Table 2 Identification result ofx1～x3

由上述表 2可得到式（10）中向量的各个元素辨识结果，进一步解方程即可辨识得到无人艇操纵运动一阶非线性响应模型中的各个参数，如表3所示。

表3 一阶非线性响应模型参数Table 3 Parameters of first-order nonlinear response model

由表3可以发现，基于AFSA辨识得到的无人艇操纵运动一阶非线性响应模型的各个参数精确度相对较高。

3 辨识结果分析与验证

为验证模型参数辨识的最终效果，对辨识所得的响应模型进行操纵运动实验仿真，并将模型输出的艏向角变化曲线与原始模型进行对比。首先，分别对原始模型和辨识模型进行20°Z形实验仿真，其艏向角的变化曲线如图7所示。

图7 20°Z形实验仿真对比Fig.7 Comparison of 20° Z test motion simulation

由图7可以看出，辨识模型所对应的艏向角变化曲线在前 60 s几乎与原始模型的艏向角变化曲线重合，误差很小。随着时间的推移，两条曲线的间距逐渐增大。这主要是由于辨识结果与原始模型参数不完全相同，必然会引起误差。而随着时间的增加，误差也不断累积，最终导致二者的偏差逐渐扩大。

考虑到在无人艇的实际运动控制过程中，舵角会实时根据需要进行改变，从而就不会受到累计误差的影响，这就说明基于人工鱼群算法的响应模型辨识结果能够较好地为高速无人艇的运动控制服务。

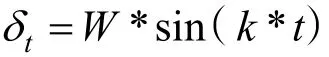
图 8-9分别为 10°Z形实验以及 20°正弦操舵仿真对应的艏向角的变化曲线对比图。

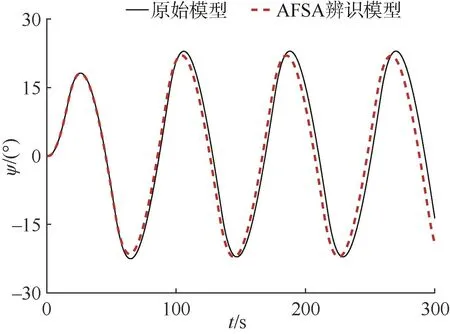
图8 10°Z形实验运动仿真Fig.8 10° Z test motion simulation

图9 20°正弦操舵运动仿真Fig.9 Simulation of 20° Sin steering motion

由图8-9可知，分别从舵角和运动类型两个维度进行改变，对辨识模型进行不同舵角以及不同类型的运动仿真，其艏向角的变化曲线与原始模型的误差较小，说明基于人工鱼群算法对高速无人艇的一阶非线性响应模型参数辨识结果具有良好的泛化能力，能够较好地适应不同舵角下的操纵运动，从而更好地实现高速无人艇的操纵运动。

4 结束语

针对高速无人艇的运动控制特性，以及其对一阶非线性响应模型的需求，本文基于人工鱼群算法对高速无人艇操纵运动响应模型的参数进行辨识，并结合相应的操纵运动仿真实验，得到如下结论：

1）基于AFSA能够实现对无人艇一阶非线性操纵响应模型参数的辨识，并且参数的辨识精确度较高。

2）基于AFSA对高速无人艇操纵模型进行参数辨识过程中，运算量小、辨识结果收敛迅速，保证精度的同时具有高效性。

3）基于人工鱼群算法辨识得到的响应模型具有较强的泛化能力，对不同舵角以及不同操舵形式下的操纵运动，都能够保证足够的准确性，从而更好地对高速无人艇进行操纵运动控制和预报。