基于有限傅立叶级数法的浮标测波算法研究

余白石，张素伟

（中国船舶重工集团有限公司第七一〇研究所，湖北 宜昌 443003）

0 引言

波浪浮标是目前常见的波浪测量仪器，由于用浮标观测波浪不受水深的限制，且具有无人值守、自动测试等优点，因此在波浪测量中广泛应用。测波浮标具有良好的随波运动特性，通过测量浮标的运动速度和位移，获取浮标的三维运动，可以计算获得波高、周期、方向谱等信息。

北斗卫星导航定位系统可以全天候提供高精度的三维位置、三维速度和时间信息，将其应用于浮标，可以测量浮标所在波浪粒子的运动速度和位移，进而通过北斗测波算法获得波浪的波高、波周期和波向等海洋水文信息。

目前国内外研究的测波算法主要为：有限傅立叶级数法（Finite Fourier Series Method）[1]、最大似然法（Maximum Likelihood Method）[2-3]、贝叶斯估计法（Bayesian Approach Method）[4-5]和最大熵法（Maximum Entropy Method）[6-7]等。

本文所介绍的测波算法为有限傅立叶级数法，该方法计算快速，易收敛，适用于较少数据阵列的波浪方向谱的计算。

1 北斗定位浮标测波原理

北斗定位浮标测波算法的输入参数主要来源于北斗定位采集器采集的定位参数，其中包括各方向的速度分量。通过输入的离散测量速度序列，在各方向积分获得各方向的离散位移序列，然后通过滤波获得低频的波浪运动分量，将获得的离散位移分量进行FFT分析，获得互谱，进而计算波浪的波高、周期和波向。图1为波浪算法的信号处理流程。

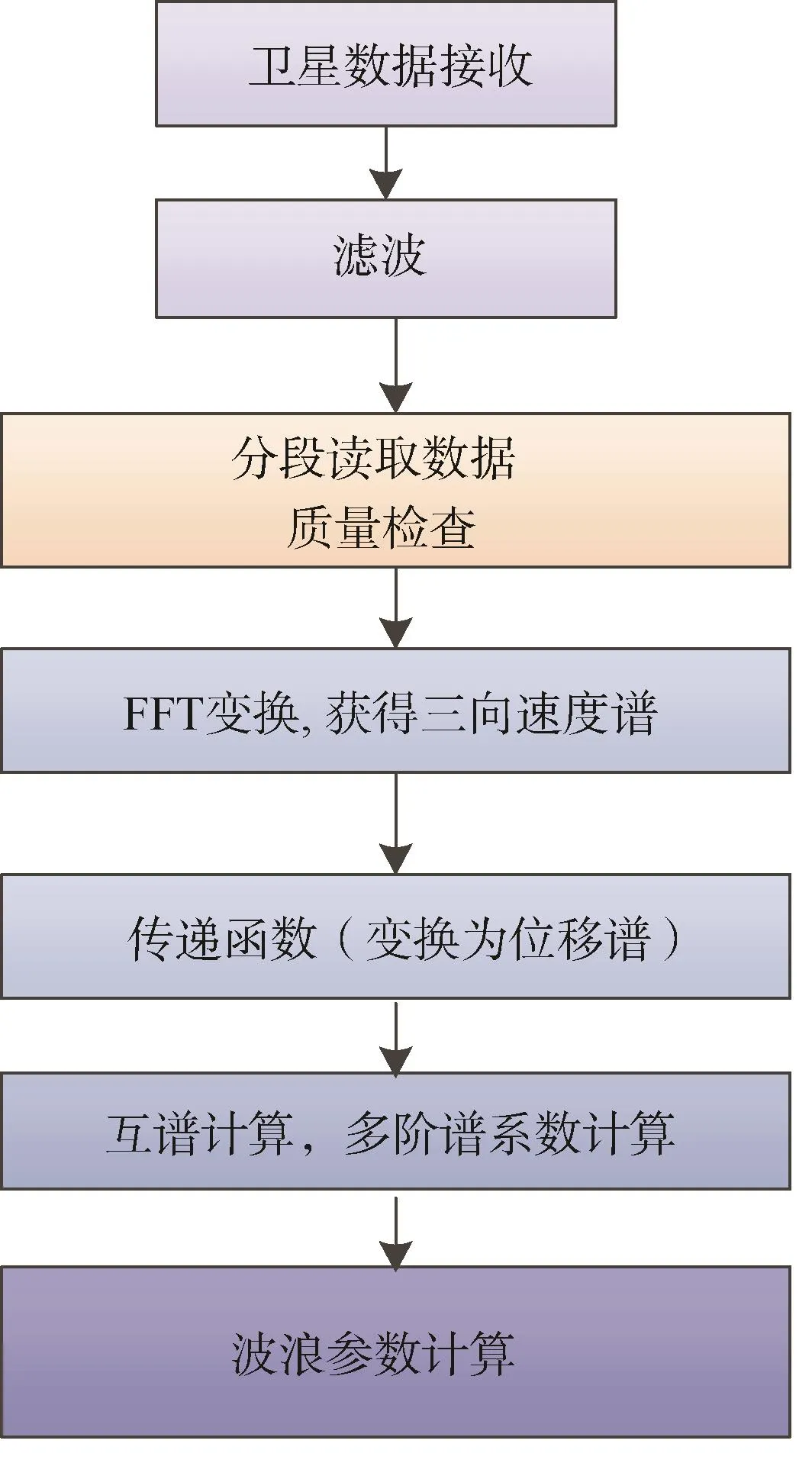
图1 北斗波浪浮标测波算法流程Fig.1 Flow of wave measurement based on BeiDou wave buoy

1.1 波浪速度谱基本理论

波浪测量理论中应用比较广泛的是 Longuet-Higgins模型[8]，其波面可以表示为无穷多个不同振幅、频率、相位和入射波的余弦波的叠加，即：

式中：η(x,y,t)表示和位置及时间有关的波形函数；ωi为成分波元频率；ki为对应于ωi的波数；θj为入射波的波向；aij和εij分别为对应于频率和波向的振幅和相位。

假设浮标完全跟随水面运动，则观测到的垂直波面位移为

η(t) 的自相关函数为

式中，τ为时延。

波谱密度 Sv(f)表示波浪在一定频率范围内所含能量，也称波浪的速度谱，可通过对式（3）求得的自相关函数R(τ)进行傅里叶变换来计算：

波浪的速度谱S(f)反映了波浪能量与频率之间的关系。在实际测量中，由于北斗定位系统输出的速度存在误差，造成北斗输出的速度谱也不能反映真实的波浪速度谱，因此需分析其误差来源，并通过滤波减小误差。

1.2 浮标测量数据滤波方法

北斗单点定位误差主要来自星历误差[9]、星钟误差[10]、电离层误差、对流层误差、多径效应、接收机噪声等。表1为以上各种误差的分析情况。

表1 北斗定位系统误差分析Table 1 Error analysis of BeiDou positioning system

为了提高北斗定位系统的测波精度，需采用带通滤波器减小北斗定位误差，从而准确提取出波浪的运动参数[11]。带通滤波函数如下：

1.3 波浪参数计算方法

要计算波浪的波高、周期和波向，必须计算方向波谱。根据 Longuet-Higgins模型，随机波浪是由无限多个不同振幅、频率、相位及波向的成分波所迭加而成，方向波谱是描述这些成分波的能量分布[12]，它是方向和频率的函数。

方向波谱的计算由互谱开始，互谱定义为交错相关函数的傅立叶变换，交错相关函数可由式（3）引申定义为

式中：η(t)为波形函数；i,j=1,2,3，表示各方向的物理观测量；η1(t)表示垂直方向；η2(t)表示东西方向；η3(t)表示南北方向；τ为时延，Rij(τ)为其交错相关函数。互谱φij(f)可用如下方法计算：

将式（7）表示为复数形式：

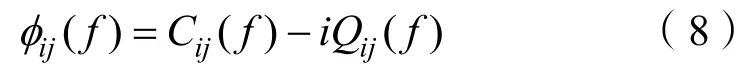
式中：Cij(f)定义为同位谱；Qij(f)定义为移位谱。互谱 φij(f)和方向波谱S(f,θ)具有如下关系：

将式（9）推到为一个计算方向波谱的通式：

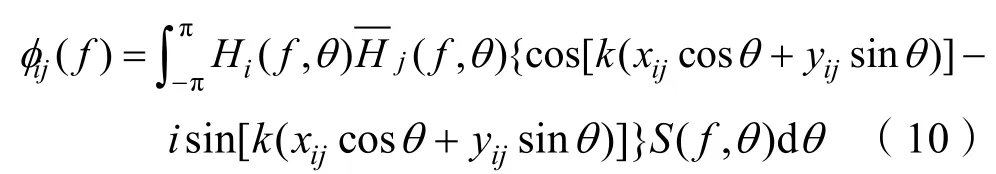
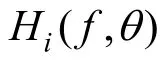
由于式（11）很难求解，式中的方向波谱可以以有限阶数的傅立叶级数展开，如式（12），再代回上式求解，此即为有限傅立叶级数法。

结合式（8）、（11）、（12），并精确至二阶，可得到各阶的系数：

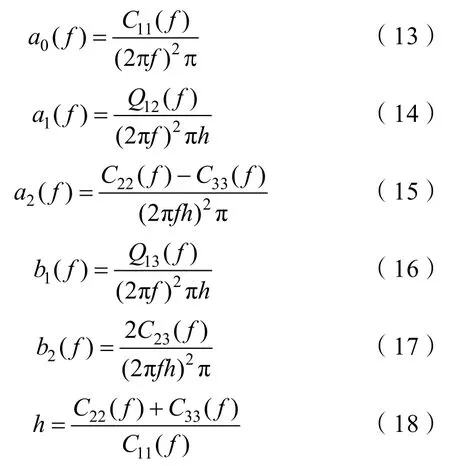
式中，m0和m2分别为方向波谱对方向及频率积分后波谱的零次矩和二次矩，具体计算方法如下：

2 测试方法

为了验证测波算法的有效性，在波浪仿真模拟器上进行了仿真测试。通过设定浮标的6种工作场景，仿真模拟器生成6种不同的浮标运动轨迹，并采用 UM330 北斗接收器采集射频模拟器输出的观测信息，对采集的信息进行数据格式转换，最终根据本文介绍的波浪测量算法计算出波浪的波高、波周期和波向。具体的测试方法流程如图2所示。

图2 北斗波浪浮标测波算法仿真测试流程Fig.2 Simulation test flow of wave measurement algorithm based on BeiDou wave buoy

2.1 载体轨迹生成

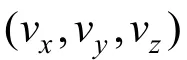
本次载体轨迹生成的圆周运动圆点为(Re+r,0,0)，其中Re为地球半径，根据输入波浪参数的不同生成不同的载体运动轨迹。波浪基本参数波高为20 m内、波向为0°～360°，波浪周期2～15 s，其中要求波浪原始观测信息采集单次20 min。图3是其中一组载体轨迹仿真示意图，其圆周运动半径r为10 m，周期T为10 s，运动轨迹倾角为Z偏Y 60°。

图3 载体轨迹示意图Fig.3 Carrier trajectory diagram

2.2 原始数据采集

载体运动轨迹生成之后，导入模拟器，用于产生射频信号，模拟器输出信号为BDS B1频点信号，信号强度-130 dB·m，仿真信号时间大概25 min，原始观测数据输出频率为 2 Hz。根据波浪所做圆周运动的半径、周期和波向，共分为6个场景来采集北斗接收器的原始观测数据，图4为北斗接收器的示意图，场景具体参数见。

图4 UM330北斗接收器采集数据Fig.4 UM330 BeiDou receiver collecting data

表2 场景参数表Table 2 Scene parameter table

3 测试结果分析

根据测试方法，测波算法测量值与原始波浪参数对比表格如表3所示。

表3 测波算法仿真测试结果Table 3 Simulation test results of wave measurement algorithm

为了进一步验证测波算法，使用某型波浪浮标开展了湖上对比测试，试验地点为漳河水库，水深约35 m，海况2级。该型波浪浮标搭载北斗定位测波模块，同时内部集成成熟的IMU测波模块。在相同试验环境下，以IMU测波模块测量数据为标准值，对北斗定位测波模块进行对比分析，如图5-7所示。

图5 波高测量数据相对误差分布图Fig.5 Relative error distribution of wave height measurement data

图6 波向测量数据相对误差分布图Fig.6 Relative error distribution of wave phase measurement data

图7 波周期测量数据相对误差分布图Fig.7 Relative error distribution of wave period measurement data

对图 5-7进行分析，在湖上波高数据集中在0.1～0.6 m内，波高测量数据相对误差分布在2%～14%范围内。波向测量数据相对误差分布在4%～10%范围。波周期数据测量相对误差分布在2%～10%范围内，且随着波周期增加，相对误差呈逐渐减小趋势。北斗定位测波模块和 IMU测波模块在三种波参数的测量上保持较好的一致性和准确性，测量相对误差维持在2%～10%范围。

4 结束语

本文对波浪浮标的测波原理和仿真测试系统进行了研究，详细阐述了基于有限傅立叶级数法的浮标测波算法，并通过仿真试验及湖上对比试验，验证了测波算法的准确性。该测波算法可应用于装载 GPS或北斗定位模块的波浪浮标，在海洋监测领域有较广阔的应用前景。