新冠疫情下“停课不停学”的大学物理GeoGebra仿真单摆实验

何秋静,杨文韬,王晓雅,支启军

(1.贵州师范大学 物理与电子科学学院,贵州 贵阳 550000；2.六盘水师范学院 物理与电气工程学院,贵州 六盘水 553004)

2020年春，各高等学校积极响应“停课不停教、停课不停学”的要求，在疫情防控中充分利用已有课程积累和网络资源，积极开展线上授课和线上学习等在线教学活动[1-3]。在此背景下，本文采用GeoGebra 5.0软件开发了手机和电脑都可以实现小球做单摆实验的过程。GeoGebra是为小学到大学的教学而设计的开源动态数学软件，GeoGebra针对不同的数学物件，提供不同的视区。不同的视区提供各自适用的工具列，包含了特定的工具、指令以及内建函数与运算子，使用者可以运用不同表征的数学物件，来创造动态结构。根据GeoGebra软件的特点，用来做物理仿真实验，可以作为物理教学的一个工具，下面以单摆为例，利用GeoGebra软件实现单摆实验的演示与仿真。

如果把悬挂的小球(摆球)自平衡位置拉至一边(摆角θ<5°)，然后释放，摆球即在平衡位置左右做周期性摆动，这种装置称为单摆[4]。单摆做简谐运动，单摆的周期与摆球质量无关，在振幅较小时与振幅无关，但与摆长有关，摆长越长，周期也越长[5-7]。单摆原理在高中甚至大学物理中占据着重要的地位，故弄清单摆的原理及特点是非常重要的。本文利用GeoGebra 5.0软件制作了小球做单摆的演示实验，在设计过程中严格遵循单摆的原理，运用微分方程推导出摆球摆动的函数关系式，提高仿真实验的可信度。学生在操作过程中，可以更深入的掌握单摆的原理，甚至比真实实验更加锻炼理论推导能力。

1 实验原理

单摆是理想的物理模型，由理想化的摆球和摆长组成，摆线的质量不计，不可伸缩[8]。

(1)如图1，摆长为L，小球受力为：重力mg和绳子的张力T。将重力进行正交分解，重力mg可以分解为沿圆弧的切向和径向的两个力,L与垂线的夹角为θ,小球的位移为x。

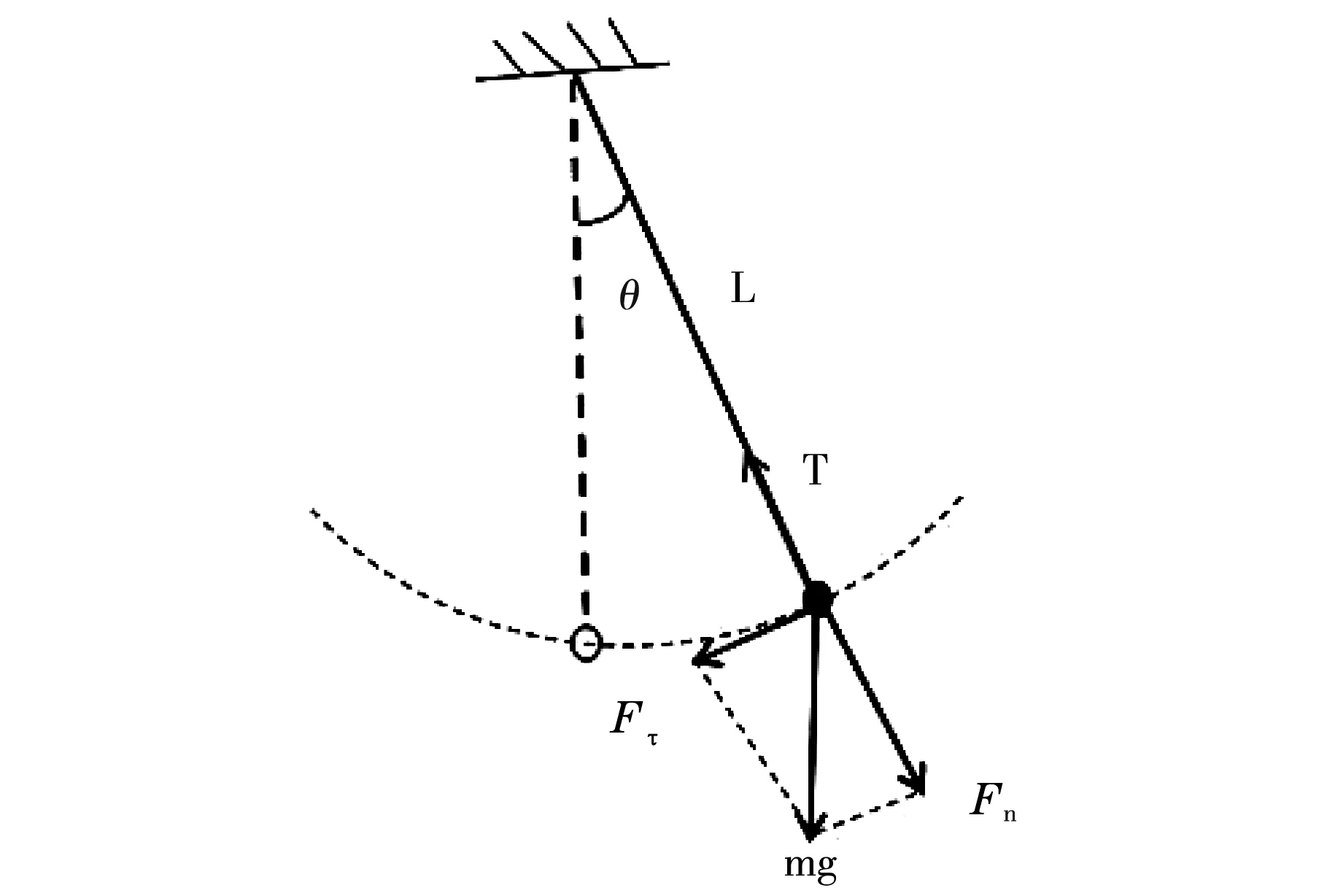
图1 单摆的受力分析图

(2)根据牛顿第二定律，可以列出小球在切线方向上的运动方程：

切线方向的微分方程为：

(1)

方程两边消去质量m得：

(2)

(3)

(4)

在切线方向小球仅受切向力，由(2-1)式可知

(5)

由Fτ=maτ

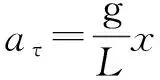
(6)

由圆周运动公式可知：aτ=ω2x

(7)

(2-7)式即简谐运动的微分方程

解微分方程得：θ=θ0sinωt，或θ=θ0cosωt

(8)

综上所述，单摆的摆动近似是简谐运动[9]。

2 用GeoGebra仿真单摆实验过程

2.1 单摆仿真实验的动态平面设计

GeoGebra是一款专门为理科生设计的动态数学软件，GeoGebra软件类似于几何画板式的几何工具，它结合“几何、代数、微积分”，可在上面画点、向量、线段、多边形、圆锥曲线、甚至函数[10]。通过单摆原理的理论推导，可知圆频率ω与摆长L有关，因此在设计过程中定义小球的数学函数是关键。

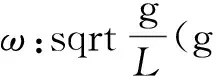
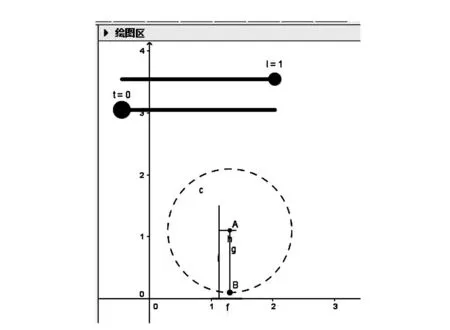
图2 单摆的动态平面效果图

在3D绘制区中，基于单摆在平面坐标系的设计步骤，可绘制出单摆摆动的立体效果，单摆3D效果图如图3所示。

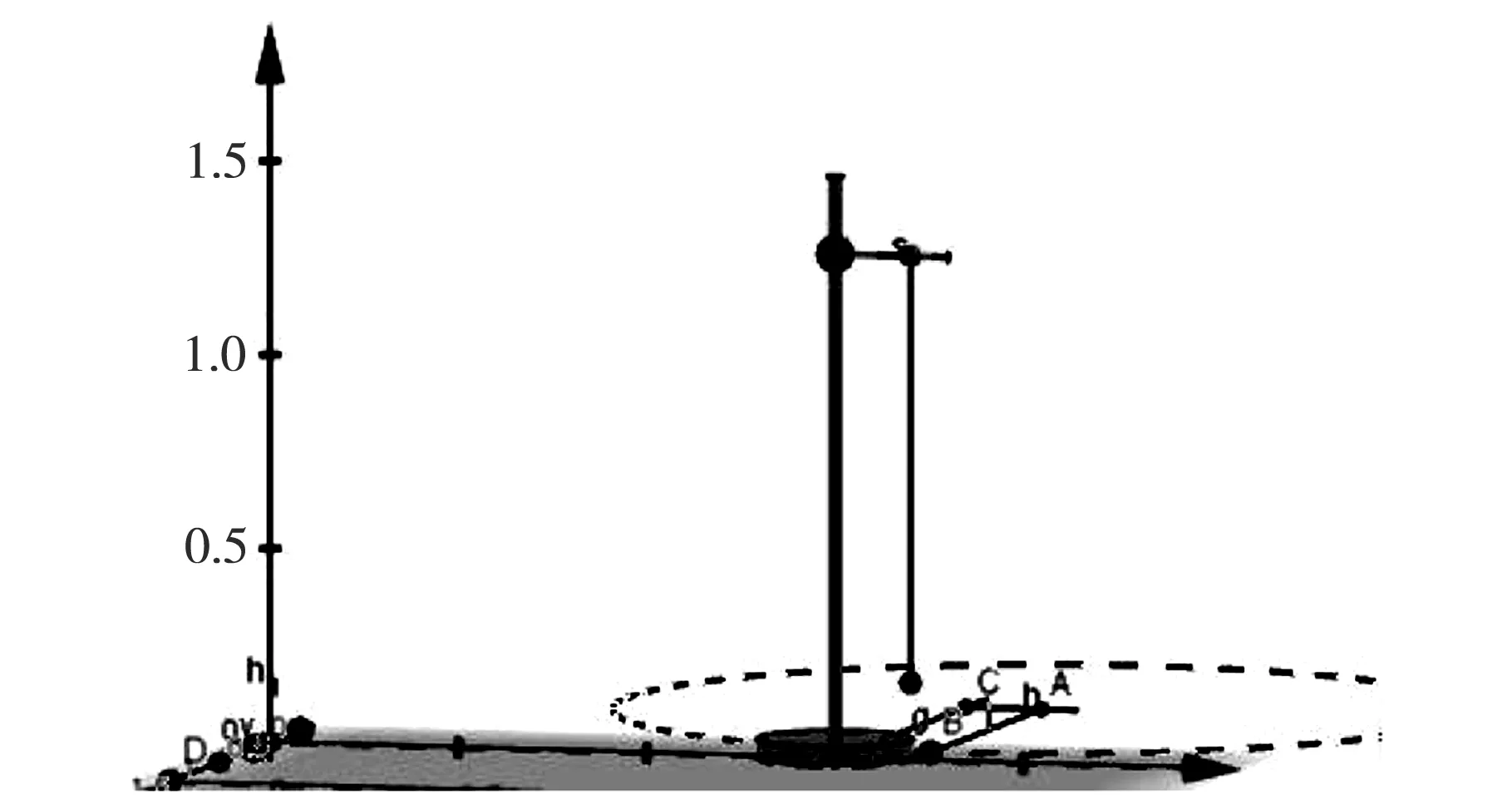
图3 单摆的动态立体效果图

2.2 单摆仿真实验的正弦函数设计

单摆的摆角很小时，质点的运动可以近似的看作简谐运动，简谐运动的状态可以用正弦函数来描述。

首先定义向量u[(0,-2),(3,-2)],作为时间t轴，再定义向量v[(0,-2.5),(0,-0.5)],作为y轴。定义动点D(0.04t,-2+0.2lsin(ωt)),作为小球的运动情况。定义时间t1:t1=0.01t。最后定义曲线j[0.04t1,-2+0.2lsin(ωt1),t1,0,t],作为正弦曲线。单摆的正弦函数图像如图4所示。

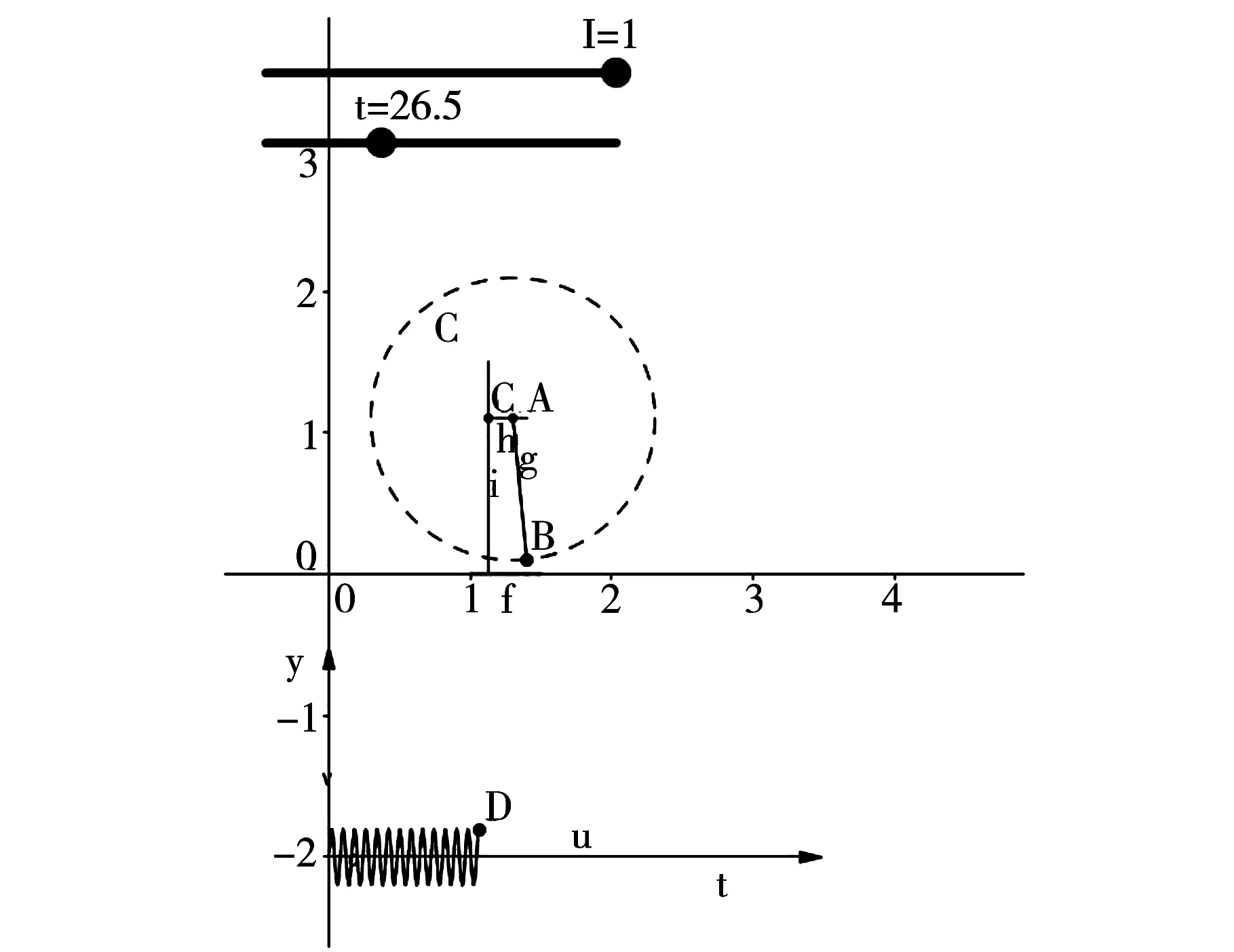
图4 单摆的正弦函数图像

3 仿真实验的分析与总结

在GeoGebra平台上设计单摆实验的过程不仅要掌握单摆摆动的简谐运动规律的理论知识，还要具备数学的逻辑能力。在制作仿真单摆实验的过程中总结出了GeoGebra5.0软件作为辅助教学的一些优点。

3.1 操作简单，调试方便

GeoGebra 5.0软件是定义数学物件来创造动态结构，平常所用到的线段、圆、曲线等，可直接用中文输入代数区，中文输入后就会显示所对应的数学格式，在绘制过程中只需把数字插入即可。在工具栏上的滑动条，可根据所设置的变量，在区间内随意调试，这样可看见不同情况下的实验效果，进而可以记录所对应的数据，这与真实实验收集多组数据的操作是一致的，且导出手机后可随时观看实验效果，可见GeoGebra平台有平易近人的特点。

3.2 仿真实验与真实实验融合度高

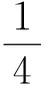
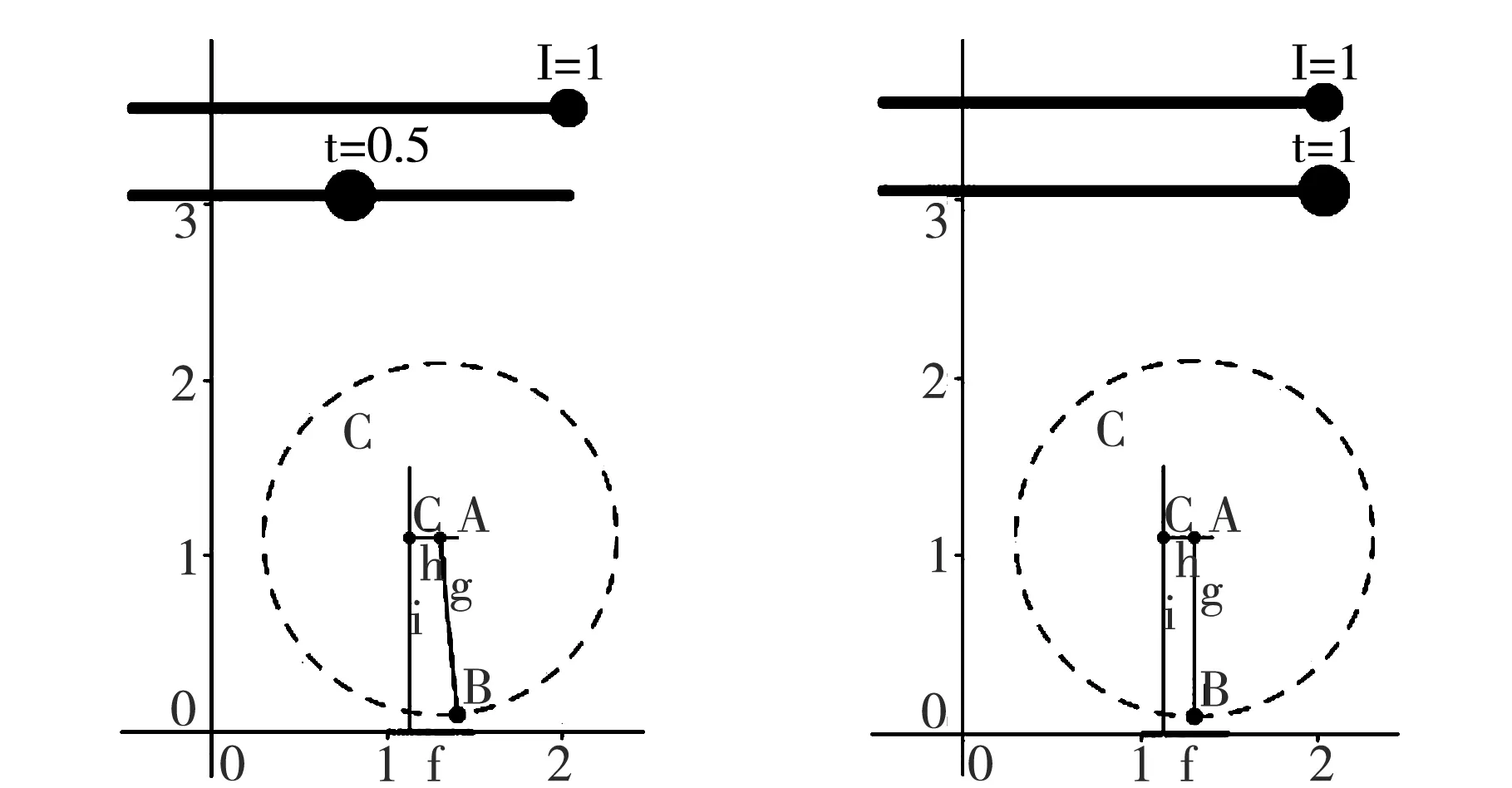
图5 小球摆过和个周期的时间图

在单摆实验中最关键的就是控制摆角小于5°，在真实实验实验中运用工具是比较容易实现的，在GeoGebra平台上如何保证小球的摆动幅度在5°以内呢？经研究讨论，结合单摆的摆动的理论知识，单摆的摆角与摆长有关，且由(8)式可知摆角是关于时间的正弦函数，故可在2.1单摆仿真实验的平面设计步骤中，起初定义点B的坐标为(1.3+0.2lsin(ωt),1.1-l)，但发现当l取很小时，摆度过大，已经不是单摆过程，从仿真来看，小球已经离开圆c运动，或者说圆轨迹运动与直线运动的简谐振动已经不重合，如图6对点B定义的效果图(a)所示。经研究讨论后定义点B的坐标为(1.3+0.1lsin(ωt),1.1-l)，这样可以始终保证小球的摆动幅度在5°之内，如图6对点B定义的效果图(b)所示。

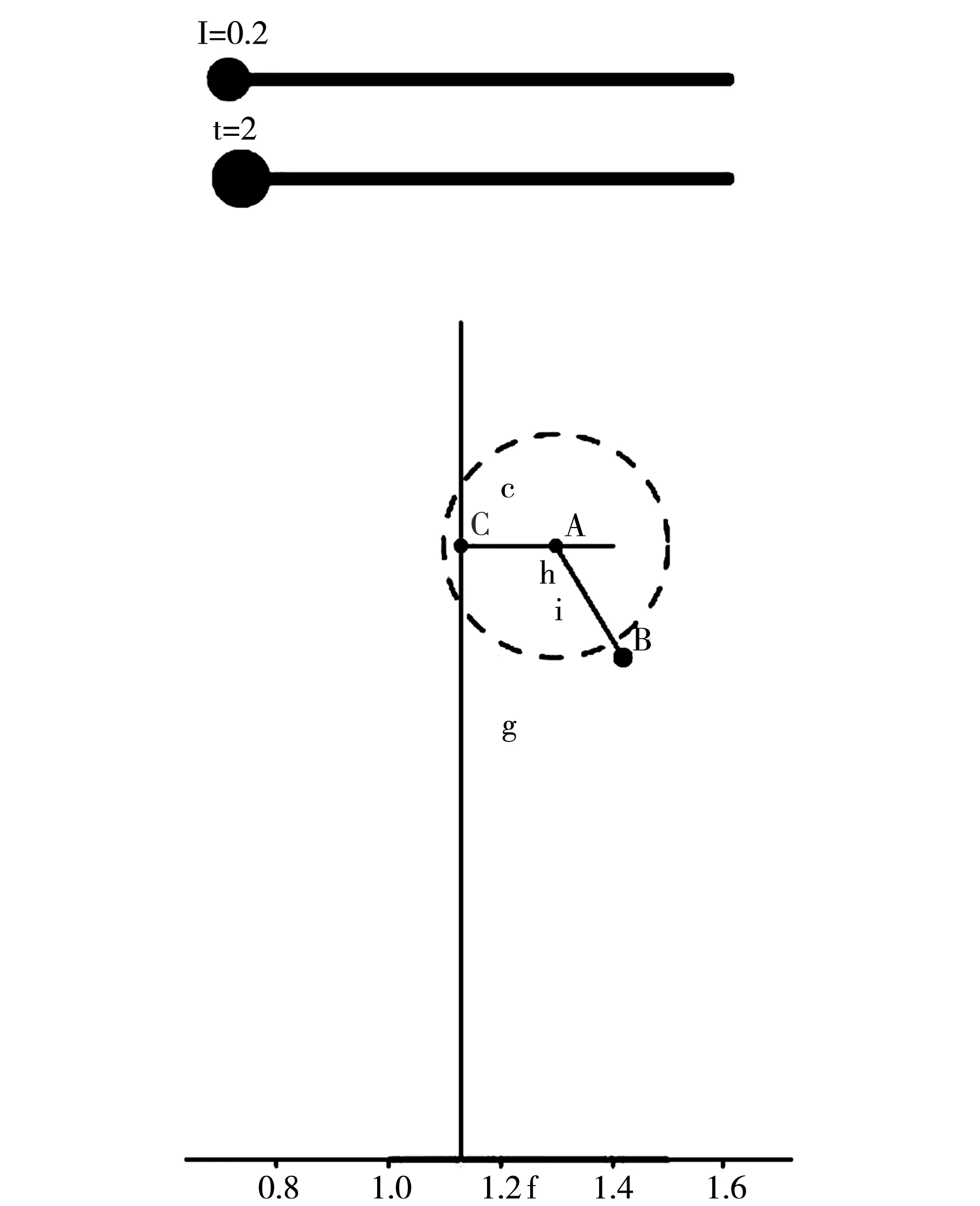
(a)

3.3 提高数学的逻辑思维能力

由于GeoGebra5.0软件是用数学公式来指令动态结构，所以在GeoGebra平台上做仿真实验时，要具备数学的逻辑思维。例如，在做单摆仿真实验的正弦函数设计时，小球摆动的时间为80时，正弦函数图很长，不能体现小球摆动的实际运动情况，且影响美观，如图7所示。

图7 单摆的正弦函数图

由于正弦函数图像太长，即x坐标太长。解决的方法就是压缩，怎么压缩函数？这就要运用数学方面知识以及逻辑思维能力，单摆绘制的正弦曲线采用参数方程绘制，将x的参数乘以一个小于1的倍数，y坐标不变就可以把函数图像的x轴压缩，从而把很长的时间压缩到一个较短的坐标轴上，如图8所示。

图8 单摆的正弦函数图

4 结 语

本文利用GeoGebra 5.0软件实现了小球单摆实验的演示与仿真，对本实验中摆角的控制以及单摆的正弦曲线进行了巧妙设计，这将有助于学生加深对小球做单摆运动规律的理解。此外，GeoGebra 5.0软件在小学至大学中作为一种辅助教学工具，在未来有很大的发展前景。不管是教师将GeoGebra 5.0软件制作的动画用于教学，还是学生拿来作为课前预习的实验,这对于物理概念和物理规律的掌握以及运用都有很大的帮助。