基于多重分形原理的大坝位移分析与预测研究
2021-05-07谢雨航邓念武刘勇军
谢雨航,邓念武,刘勇军
(1.武汉大学水利水电学院,湖北 武汉 430072;2.中国长江三峡集团有限公司,湖北 宜昌 443133)
作为一门新兴的理论体系,分形理论有独特的魅力,目前已经被证实该理论可以较好地应用到自然科学以及社会科学中[1]。用分形理论分析杂乱无章的复杂系统,可发现它们仍然具有数学规律,分形理论为时间序列分析供了新的分析途径。大坝安全监测数据属于时间序列,监测数据也具有随机性、多尺度变化等复杂的特性,分形理论可以有效识别时间序列包含的内在规律。本文将从多重分形去趋势波动分析、非对称多重分形去趋势波动互相关分析及分形预测等方面对多重分形进行研究,以分析非平稳时间序列,评估两时间序列的相关性并预测大坝位移发展趋势。
1 多重分形理论
1.1 多重分形去趋势波动分析(MF-DFA)原理
Kantelhardt J W和Zschiegner S A等学者结合去趋势波动分析(Detrended Fluctuation Analysis,简称DFA)方法与多重分形理论(Multifractal theory,简称MF)[2],改进性地提出了MF-DFA方法。该方法统计时间序列在每个分割区间上波动的平均值,计算时间序列波动函数的幂律性和广义Hurst指数,运用Hurst指数衡量时间序列结构的平稳和非平稳性,并使用多重分形奇异谱衡量时间序列波动的奇异性,能准确分析非平稳时间序列的长程相关性,并能够避免对时间序列相关性的误判。MF-DFA对非平稳时间序列的多重分形特性分析更具优越性。
1)构造新的时间序列。假设有一个时间序列xi(i=1,2,3,…,n),现构造新的时间序列Xi:
(1)
2)分割时间序列。将时间序列Xi以相同的长度s(5≤s≤n/4)分割成不重叠的ns(ns=int(n/s))段数据,为充分利用数据的长度,再从数据的反方向用相同的长度分段,得到2ns段数据。
3)利用最小二乘拟合计算序列2ns个区间中每个区间的局部趋势:
(2)
则整个序列的q阶波动函数Fq(s)为
(3)
(4)
4)计算广义Hurst指数h(q)、标度指数τ(q)、奇异谱f(α)与奇异指数α:
Fq(s)∝sh(q)
(5)
对ln[Fq(s)]做ln(s)的一次线性拟合关系图,一次项系数即q为阶广义Hurst指数h(q)。
h(q)与标度指数τ(q)有关,其解析关系试如下:
τ(q)=qh(q)-1
(6)
对于描述多重分形序列的方法是奇异谱f(α),可利用勒让德(Legendre)转换得到f(α)与τ(q)之间的关系:
α=τ′(q)=h(q)+qh′(q)
(7)
f(α)=q[α-h(q)]+1
(8)
奇异指数α用来描述序列的尖顶、峰值、波动和频率等奇异性特征[3]。
1.2 非对称多重分形去趋势波动互相关(AMF-DCCA)分析
在复杂的系统中,常有效应量序列受到自变量序列的影响而发生变化,而MF-DFA方法只能反映时间序列的自相关特性,无法体现效应量序列与自变量序列之间的联系。通过在效应量序列中引入非对称的思想,提出了非对称多重分形去趋势波动互相关分析(AMF-DCCA)方法[4],评估两时间序列是否存在非对称相关性,算法如下:
1)假设有两个长度均为n的原型观测序列xi,yi(i=1,2,3,…,n),构造新的时间序列Xi,Yi:
(9)
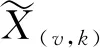
(10)
以原型观测序列xi为例,q阶平均波动函数为:
(11)
(12)

3)对比MF-DFA方法,得出平均波动趋势的波动函数为:
(13)
4)通过q阶波动函数Fq(s)与时间尺度s之间存在的幂律关系可以计算广义Hurst指数h1(q):
(14)
式中,h1(q)为广义Hurst指数,但h1(q)表示的是两个相关序列之间的互相关性。
1.3 分形预测理论
根据分形应用中的数学基础与方法[5-6]中的定义,分形维数可近似地表示为
N=C·r-D
(15)
式中:r为特征线度,如长度和时间等;N为r对应的量,如大坝安全监测中的位移、温度和水位等;C为待定常数;D为分维数。
分维数D为常量时的分形分布称为常维分形,(ln(Ni),ln(ri))呈线性关系,根据该直线上的任意两个数据点可以确定该段直线的分形参数分维数D和常数C:
D=ln(Ni/NJ)/ln(rj/ri)i≠j
(16)
C=Ni·rD
(17)
设N与r之间的函数关系为N=f(r),对于常维分形分布有f(r)=C/rD,求解出r得到任一函数关系的常维分形形式:
r=[C/f(r)]1/D
(18)
在实际应用中函数关系通常是未知的,只存在一系列的数据点(Ni,ri),因此需要寻找恰当的变换方法,以求出变换的具体形式。运用施行累计和的系列变换r和N,将数据进行一系列的变换,从中选出一种变换,让变换后的数据能够用分形分布来处理。变换方式如下:
由于ln(Ni),ln(ri)(i=1,2,…,n)在一般情况下不能与分形分布模型符合良好,于是运用公式(1)将Ni构造一阶累计和序列S1i:
(19)
同样可以构造二阶、三阶及多阶累计和序列S(J)i(J为阶数)。
建立各阶累计和序列的变维分形模型,通过公式(16)求得各阶的分形参数分维数D;比较各阶分段变维分形模型,并选择效果最好的变换,运用外插的方法开展预测计算工作。
2 实例分析
福建某双曲拱坝,坝顶高程346.5 m,最大坝高81.5 m,坝顶中心线弧长153.676 m,坝顶设6个水平位移监测点,如图1所示。本文采用2007年1月至2015年12月共9年大坝径向位移和环境量数据进行MF-DFA分析、AMF-DCCA分析以及分形预测。
2.1 大坝位移时间序列多重分形去趋势波动分析
根据大坝变形监测资料的周期性波动趋势,结合时间尺度的合理取值,取时间尺度s=6,9,12,15,18,21,24,单位为月,根据MF-DFA算法得到各时间序列的h(q)~q关系图和f(α)~α关系图。

图1 大坝水平位移监测点位布置图
图2与图3分别为温度、水位和各测点径向位移广义Hurst指数h(q)~q关系。当q=2时,水位和温度时间序列的h(2)值分别为0.69和0.61,各观测点时间序列的h(2)值均大于0.5,说明水位与温度和各测点时间序列存在长程相关性。整体上看,温度序列的大或小波动标度变化都较水位的大或小波动标度变化显著;由于大坝处于稳定的运行期,可以看出各测点序列的小波动标度单调递减较各测点的大波动变化明显,说明各测点出现小位移的概率较高。

图2 环境量时间序列关系曲线图

图3 各测点时间序列关系曲线图
图4为各测点时间序列多重分形奇异谱曲线。位移观测点A、B、C、D、E和F的分形奇异谱宽度Δα分别为1.279、0.523、1.149、0.573、1.150和1.026,奇异谱高度Δf(α)分别为-0.035、0.524、0.558、1.010、0.449和0.074。观测点C和D时间序列奇异谱高度Δf(α)>0,且明显大于其他测点时间序列奇异谱高度,说明该两测点位移时间序列中大位移出现的概率较高。由图1可知,观测点C和D位于拱坝的中间位置,当环境量变化时位移变化会较大,拱坝中间部位位移量较大,符合拱坝的变形规律。

图4 各测点时间序列多重分形奇异谱曲线图
2.2 大坝位移时间序列多重分形去趋势波动互相关分析
大坝位移监测序列的AMF-DCCA分析旨在分析大坝位移时间序列与环境量时间序列之间的相关程度,环境量的变化直接影响到大坝位移的变化,由于篇幅有限,选取A、C测点的位移时间序列为主要研究对象,验证和分析大坝位移时间序列与环境量时间序列的互相关特性。由图5各测点的h(q)~q函数关系图可知,随着q值的增大,h(q)单调递减,说明各测点位移时间序列与环境量之间存在互相关性,大坝位移时间序列的波动受到环境量时间序列波动的影响,符合大坝的变形规律。由图中可以看出,两测点h(2)均大于0.5且小于1,说明大坝位移时间序列与环境量时间序列存在长程相关性,即环境量时间序列的改变会对大坝位移时间序列变化产生影响。当q<0时,各测点环境量的h(q)变幅较q>0的大,说明环境量小幅度波动对大坝位移时间序列的互相关特性影响较大幅度波动的大,尤其温度的小幅度波动最为显著,即温度时间序列的小幅度波动对大坝位移时间序列的波动影响较大。

图5 测点位移时间序列与环境量间的h(q)~q关系曲线图
2.3 大坝位移时间序列多重分形原因判定
为了运用分形预测理论对大坝变形开展预测工作,首先对影响大坝位移监测时间序列多重分形特性形成的原因进行分析。由于篇幅有限,仅选取测点A和C进行分析。
时间序列表现出多重分形特性的原因主要来源于两个方面:①时间序列的非正态分布;②时间序列的长程相关性。对原始时间序列进行随机重排得到重排序列,相位随机化处理原始时间序列得到替代序列,根据原始序列、重排序列和替代序列可以有效区分上述两种原因对多重分形的贡献程度。
现对原始时间序列和重排后序列进行MF-DFA分析。根据MF-DFA算法取时间尺度s=[6,9,12,15,18,21,24],取波动函数阶数q=[-10,-8,-6,-4,-2,0,2,4,6,8,10],最小二乘拟合阶数m=1,得到各位移测点的原始序列、重排序列和替代序列的h(q)~q关系如图6所示。
由图6的两测点位移时间序列h(q)~q关系曲线图可知,重排序列的非线性特征明显弱于原始序列,说明原始序列和替代序列的多重分形特性较强。即大坝位移时间序列的多重分形特性主要是长程相关性引起的。

图6 测点位移时间序列h(q)~q关系曲线图
图7为测点A、C的q~ln(s)~ln(Fq(s))三维函数关系图。当q值由-10至10之间变化时,在时间尺度s较小时,波动函数值之间的差异明显,而在时间尺度逐渐变大时,波动函数值之间的差异逐渐变小,说明小的时间尺度能够识别局部时间内的大小波动,大的时间尺度在一定程度上均化了大小波动的幅度。因此在做大坝变形预测时,选择时间尺度s=12,即以年周期进行预测效果较好。

图7 q~ln(s)~ln(Fq(s))三维函数关系图
2.4 大坝位移时间序列分形理论预测分析
以测点A、C从2007年1月21日至2015年12月18日的测值序列为例,按照上述方法,计算1~3阶的分段维数值,并作出两测点的分段维数图。
由图8与图9可看出,一阶分段维数图波动范围最小,尾部也较平直,可以基于一阶分段维数运用2007年1月21日至2014年12月23日期间序列建立模型,预测2015年1月23日和2015年12月18日期间的测值。测点A和C的实测值、预测值和残差如表1所示。

图8 A测点平移处理时间序列分段维数图
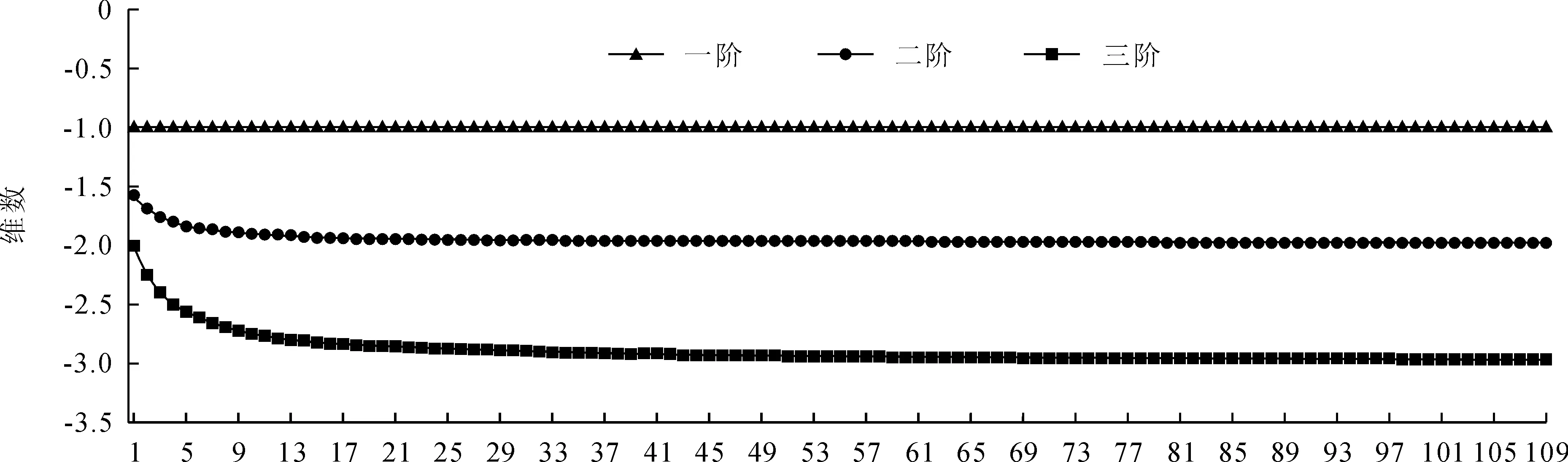
图9 C测点平移处理时间序列分段维数图

表1 测点A、C实测值、预测值和残差统计表 mm
3 结 语
本文利用多重分形原理对大坝位移进行分析研究,并进行了实例分析。MF-DFA分析表明,该大坝坝顶各测点出现小位移的概率较高,且拱冠出现大位移的概率大;AMF-DCCA分析表明,温度变化对大坝位移时间序列的波动影响较大;运用分形预测理论,对各测点径向位移时间序列进行了拟合和预测,结果表明分形预测理论可以很好地应用到大坝位移分析中。相信随着分形预测理论的不断发展,分形预测理论对大坝安全监测资料的分析和研究将会更加深入。
