戏说复变函数闭路积分

（西安工业大学 陕西·西安 710032）

复变函数是高等院校工科专业的一门专业基础课，在其后续的专业课中有着广泛的应用。复变函数主要的研究对象是解析函数，而复变函数的积分是研究解析函数的重要工具，因此学好复变函数的积分特别是闭路积分成为了一个亟待解决的问题。但课程本身由于内容抽象，知识点多，部分同学数学底子差等，所以导致学习效果并不尽如人意。为了提高同学的学习兴趣，使得同学们对知识更容易识记，本文尝试在“戏说方式下创造一个的情景”，引入复变函数闭路积分的各种方法，并附以相应的例题，并且分析了“积分方法一家子”的区别和联系，以帮助进一步加深理解和记忆，从而轻松解决闭路积分的相关问题。

1 复变函数闭路积分方法“群英会”

话说复变函数的闭路积分，真可谓方法众多、功能各异，他们就如那“八仙过海，各显神通”，在积分计算的大舞台上大放着异彩。

其中龙头老大当属柯西-古萨（定理）（也称柯西积分定理），它独树一帜，做事干脆利索。管你被积函数形式再复杂，猴子猴孙（被积函数的奇点）再多，只要你不犯我地盘（奇点不落在积分路径内），我决定放你一马，多余的功夫跟你不费，结果为0，一遍好好歇着！

柯西-古萨定理：

积分路径有一奇点？哈哈，你还敢来烦老大——柯西-古萨（定理）？好自为之，赶紧绕道吧（柯西-古萨定理不再适用）。那谁来替俺主持公道（那咋算）？哼哼，江湖自有英雄！

积分方法1：迎面走来“例题哥”（典例结果）

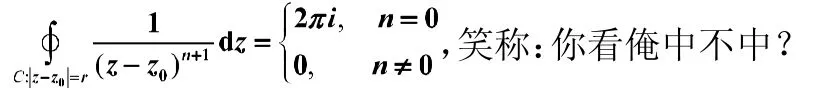
嗯，例题哥在那弄啥咧？莫非相亲吗？大哥快来！柯西积分公式大声呼叫高导公式：咱也凑凑热闹，打个擂台，看看俺们行不行？

积分方法2：打扮好（变了形）的柯西积分公式精彩亮相：

积分方法3：换了造型（变了形）的高导公式盛装出席：

恁俩啊？说中也中，说不中也不中；有时中，有时不中；要看对象是谁咧。

啥？还有比俺们高的神？

积分方法4：罗朗展式法。

例3还可以用如上留数规则1计算（其实柯西积分公式与其一致，但此处更容易，因为不需要对被积函数进行变形整理）。

留数计算规则2（m级极点）：

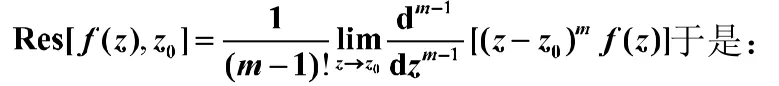
积分方法6：

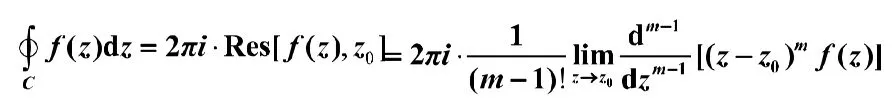
例4还可以用如上留数规则2计算。（其实高导公式与其一致）

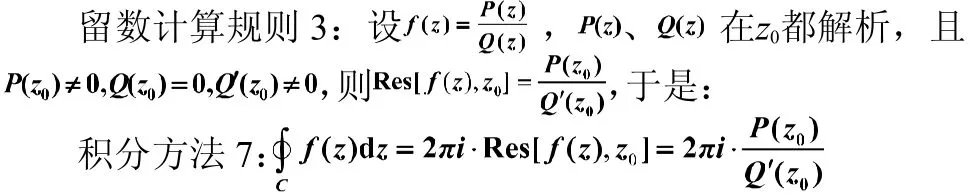
例3还可以用如上留数规则3计算（比柯西积分公式和留数规则1更容易，因为不需要对被积函数进行变形整理，另外计算更简便，且本质上是一回事）。厉害了，额滴那个神啊！

神仙偶尔也失手，你来看看有没有？

路径里面多奇点，只能复合闭路“挖奇点”，加上积分的留数新知识，刚好整出积分计算之留数两定理。留数定理一上场，从此积分它最响（尽量都用留数方法做）。内部不行转外部，无穷远点留数（规则4）来帮助。这种方法好处多（方法指的是留数定理并留数计算规则），简便易行少繁琐（不用“挖奇点”）；这种方法思路阔，所有积分都能做。

积分计算方法8留数定理+规则4：

山外青山楼外楼，无穷远点（的留数法）你最牛。

哈哈，兄弟们！有缘千里来相会，赞来赞去也不是个事儿！

其实咱们都是一家子，所以千万别客气。为求积分聚一起，奇点在哪是大问题：

路径内部无奇点，柯西-古萨最长脸。路径内部一奇点，积分方法脑海闪。

路径内部多奇点，留数定理来帮咱。各种方法来列队，积分不再是个事（儿）。

2 聊聊复变函数闭路积分方法的“一家子”

说复变函数闭路积分方法都是一家子，其实是因为复变函数闭路积分的几种方法相互之间都有着紧密的联系，有的甚至是一回事。在授课过程中，我们是这样处理的，在柯西-古萨定理的基础上推出了复合闭路定理；利用复合闭路定理和“例题哥”结果引出了柯西积分公式的思考，并在复合闭路的基础上证明了柯西积分公式；根据柯西积分公式证明高阶导数公式；“例题哥”又是柯西积分公式和高导公式的特殊情况（被积函数分子为1）；在高导公式的基础上，推出了解析函数的泰勒级数和洛朗级数；并对解析函数的罗朗展式两端进一步进行积分探讨，引出了留数定义；并利用复合闭路定理给出了复变函数闭路积分的留数定理；从此就将复变函数的积分运算转化成了留数的计算；紧接着根据孤立奇点的分类，进一步探讨了留数计算的四个常用规则。当积分路径内部只有一个奇点时，柯西积分公式计算积分跟利用“留数定理和规则1”计算是一回事；高导公式计算积分跟利用“留数定理和规则2”计算也是一回事。特别是当积分路径内多奇点时，利用留数定理和几个规则联合处理，就省去了“挖奇点”或者利用柯西积分公式和高导公式常常要把被积函数对着适用的函数特征进行整理的麻烦；特别是连同无穷远点处的留数一起切切实实解决了前面的那些方法在某些问题上不能解决的麻烦。

举例说明柯西积分公式与“留数定理+规则1”的一致性，如下：

当积分路径内部有唯一奇点且是一级时，可以用柯西积分公式，也可以利用留数定理+规则1的计算方法。这里要注意公式和定理中的被积函数的书写形式，原来定理中符号虽然一样，其实意义不同，这里区分开来，后者用表示，因为是被积函数的一级极点，所以可以写成这样的形式，，所以有：

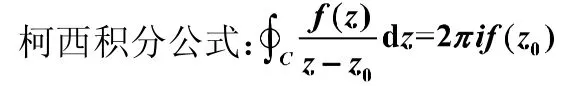
留数定理+规则1：

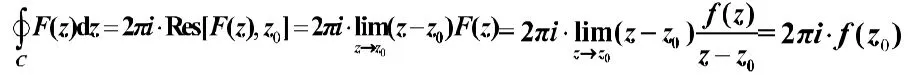
由此看见两者是一致的。

3 小结

文中在戏说各种闭路积分方法时，采取情景化的模式，自然引出各个积分方法和对应的例题分析，并进一步分析了各种方法之间的联系，理清了方法的本质，分析了各方法的优劣。总之，在积分计算时，当积分路径内部没有奇点时，利用柯西-古萨定理直接结果为0；当积分路径内部有奇点时，不管一个还是多个，最好采取“留数定理+留数计算规则”的各种组合模式。当然了，有的同学可能会先入为主，喜欢用前面的积分方法也是可以的，总之，多记一些方法和例题，认真分析和揣摩，举一反三才能顺利应对各种复变函数闭路积分计算的问题。