基于E/CRC磨损模型的离心泵壁面磨损特性研究
2021-05-07赖芬王凤鸣朱相源常沛然李国君
赖芬, 王凤鸣, 朱相源, 常沛然, 李国君
(西安交通大学 热流科学与工程教育部重点实验室,陕西 西安 710049)
泵是把机械能转化为流体压力能的通用机械,其中离心泵使用最广泛,特别是在水利水电工程中。但环境恶化引起的泥沙流失导致河流中含有泥沙,例如,中国的黄河泥沙含量为37.8 kg/m3[1],美国的科罗拉多河泥沙含量为10 kg/m3[2]。水利水电工程中的离心泵一般按清水工况设计,但其内部的实际流动为液固两相流动。固体颗粒的存在不仅会降低离心泵的效率,还会对离心泵壁面造成侵蚀磨损。磨损将导致频繁地维修和更换过流部件,造成输运系统停机,输运费用大幅度增加。Wilson等[3]指出大型矿场每小时的停机成本大约为10万美元。因此,研究黄河和长江流域使用的含沙水离心泵内的液固两相流动及其磨损特性具有重要意义。
但固体颗粒引起的壁面磨损是个复杂过程,最终的磨损形态受很多因素的影响,包括颗粒特性、流场特性、壁面特性等。国内外学者对壁面磨损的影响因素进行了大量的试验研究。例如,Tian等[4]通过科里奥利磨损试验台测试了不同颗粒粒径下壁面的磨损系数,结果表明颗粒形状、粒径分布等颗粒特性会对磨损系数产生重要的影响。陈红生等[5]通过离心泵液固两相流水力试验,发现造成局部磨损的重要原因是叶轮出口附近的射流-尾流结构。Wiedenroth[6]采用超声设备测试了4种叶轮叶片的磨损量,发现当颗粒撞击角较大时,硬度高的壁面受到的磨损较严重。
随着计算机技术的迅猛发展,数值模拟方法已成为研究各种物理现象的重要手段。目前关于离心泵液固两相流的数值模拟及磨损预测,磨损模型主要选用Finnie[7]和Tabakoff[8]模型,研究对象主要针对离心泵的某一过流部件[1,9-11]。例如,Noon等[9]应用Finnie磨损模型预测了石灰浆输送泵蜗壳的磨损形态,结果表明蜗壳的磨损率随撞击速度、质量浓度、颗粒粒径的增大而增大。刘娟等[10]应用Finnie磨损模型对低体积分数的离散相颗粒在离心泵中的运动规律及叶轮壁面的磨损特性进行了数值研究,发现液固相密度差距越大,固体颗粒的运动跟随性越差,固体颗粒与过流表面发生碰撞的几率增大,叶轮壁面的磨损强度增加。黄先北等[1]采用Tabakoff 磨损模型对不同泥沙及不同入口工况下离心泵叶轮壁面的磨损规律进行了探索,发现颗粒粒径会显著影响叶轮壁面的磨损形态和位置,颗粒在离心泵入口分布越均匀,壁面磨损越分散,磨损位置轴对称性越明显。何创新[11]采用Tabakoff 磨损模型对单级双吸中开式离心泵叶轮壁面的磨损特性进行了分析,结果表明叶轮入口前的密封体导叶能有效地抑制叶片的磨损,合理的叶片型线设计可以显著降低叶片压力侧的磨损。
然而,大部分磨损模型的建立和推导都是基于气固两相流试验的。磨损模型能否准确预测液固两相流下的壁面磨损特性需进一步验证。Zhang等[12]研究表明侵蚀磨损研究中心(E/CRC)提出的磨损模型不仅适用于气固两相流动,而且在液固两相流动中也能获得准确的结果。Peng等[13]指出E/CRC磨损模型与其他磨损模型相比,在CFD软件中更易执行,模型中考虑了颗粒硬度和形状因素,得到的数值结果与试验结果更接近。但现有研究中未见采用E/CRC磨损模型预测离心泵壁面磨损特性的研究。因此,本文针对黄河和长江流域使用的含沙水离心泵展开了研究,建立了基于E/CRC磨损模型的离心泵壁面磨损特性预测数值方法,对各个区域的磨损形态进行了预测并对比了不同区域的最大和平均磨损率,分析了磨损率变化规律并预测了最大磨损率发生位置,另外还讨论了颗粒粒径及浓度对离心泵叶轮磨损特性的影响。
1 液固两相流及磨损预测数学模型
本文采用的流动介质为黄河、长江流域的含沙水,根据长江夏季泥沙浓度[14]及黄河多年平均泥沙浓度[15],泥沙浓度大约为32 kg/m3,体积分数小于3%,泵内流动为低浓度液固流。文献[16]指出欧拉-拉格朗日方法的使用条件是离散相体积分数小于10%~12%。因此,本文符合欧拉-拉格朗日方法的使用条件,为了提高计算精确性,本文选用双向耦合的欧拉-拉格朗日方法求解。计算时忽略颗粒与颗粒间的相互作用力,并假定液固相之间没有质量和能量交换。计算时将液体视为连续相,液体流场通过在欧拉坐标系中求解雷诺时均方程获得;将固体颗粒视为离散相,固体颗粒运动通过在拉格朗日坐标系中求解颗粒轨迹方程获得。液体湍流脉动引起的颗粒扩散采用随机游走模型。颗粒撞击壁面后发生的动量变化由Grant 和Tabakoff(G&T)[8]提出的颗粒碰撞反弹模型模拟,磨损率由E/CRC 提出的磨损模型进行计算,详细的数学模型如下。
1.1 连续相控制方程
1) 质量守恒方程:
(1)
2) 动量守恒方程:
(2)

(3)
式中:μt为湍流粘度;μt由标准k-ε模型确定[17-18];k为湍动能;δij为“Kronecker delta”符号。
Fi为动量交换源项分量,Fi从以下方程获得:
(4)

1.2 离散相控制方程
文献[16]指出颗粒相动量源项主要来自拖曳力、重力、虚拟质量力、压力梯度力、热泳力、布朗力、Saffman 升力和Magnus升力产生的动量。但热泳力主要是由温度梯度引起的,离心泵中温度变化很小,因此,本文忽略了热泳力;布朗力和Saffman 升力只有处理亚微观粒子时才考虑,Magnus升力只有处理旋转粒子时才考虑,本文所考虑的粒子不是亚微观粒子,也不旋转,因此,本文忽略布朗力、Saffman 升力和Magnus升力,只考虑拖曳力、重力、虚拟质量力和压力梯度力产生的动量源项。
(5)

(6)
式中:dp为颗粒直径;μ为液体的分子粘度;Cd为拖曳系数,定义为:
(7)
式中:a1、a2、a3为由Morsi等[19]给定的常数,Re为相对雷诺数,定义为:
(8)
Fv为用于加速颗粒周边流体的虚拟质量力矢量,定义为:
(9)
Fp为液体中的压力梯度力矢量,当固体颗粒通过高压区时,它对颗粒轨迹有着重要的影响,定义为:
(10)
1.3 随机游走模型
颗粒轨道方程中的流体速度采用瞬时速度来考虑颗粒的湍流扩散,并计算足够多的代表性颗粒的轨迹来考虑湍流对颗粒的随机性影响。计算时考虑颗粒与流体的离散涡之间的相互作用,流体的脉动速度假定为时间的分段常量函数,在涡团的特征生存时间内脉动速度保持为常量,满足高斯概率密度分布函数的随机脉动速度u′、v′、w′为:
(11)
(12)
(13)
(14)
式中ζ为服从正态分布的随机数。
涡团的特征生存时间定义为常量:
(15)
式中:TL为流体的拉格朗日积分时间尺度;k为湍动能;ε为湍动能耗散率。
1.4 G&T颗粒碰撞反弹模型
Peng等[13]对比了2种颗粒碰撞反弹模型和5种磨损模型预测的结果,结果表明G&T颗粒碰撞反弹模型结合E/CRC磨损模型预测的结果与试验结果最接近,因此,本文选用G&T颗粒碰撞反弹模型。模型中,颗粒撞击壁面后,其垂直于壁面切线方向的动量变化率为法向恢复系数Vn2/Vn1,其平行于壁面切线方向的动量变化率为切向恢复系数Vt2/Vt1,分别定义为:
Vn2/Vn1=0.993-1.76β+1.56β2-0.49β3
(16)
Vt2/Vt1=0.988-1.66β+2.11β2-0.67β3
(17)
式中:Vn、Vt分别表示颗粒撞击速度的垂直分量和切线分量, m/s;下标1、2分别表示撞击前和撞击后;β为颗粒撞击角, rad。
1.5 E/CRC磨损模型
颗粒撞击壁面后,对壁面造成的磨损与壁面材料、颗粒特性、撞击角等因素相关。与其他磨损模型相比,E/CRC磨损模型考虑了颗粒硬度和形状因素,得到的数值结果与试验结果更接近。E/CRC磨损模型中磨损率计算方程为[12]:
(18)
(19)
式中:ER为磨损率(每单位面积的质量损失),kg/m2;C和n分别取值2.17×10-7,2.41;BH为布氏硬度;FS为颗粒形状系数,对于球形颗粒取值为0.2;Vp为颗粒速度,m/s;β为颗粒撞击角, rad;Ai值见表1。

表1 Ai值Table 1 Values of Ai
1.6 数学模型验证
由于文献中关于离心泵壁面磨损率的试验数据较少,因此,本文采用直径为50 mm、曲率半径为76.9 mm的 90°弯管试验对数学模型进行验证。虽然离心泵涉及旋转部件,整体结构与弯管不一致,运动条件也有差别,但由磨损模型可知,磨损率主要与颗粒形状、硬度、速度、撞击角和局部壁面特性有关,与是否涉及旋转部件和设备整体结构无关。运动条件差别将导致磨损模型中的撞击角和撞击速度差别,也就是说磨损模型中考虑了运动条件的差别。因此,弯管试验是可以验证数值模拟方法的。
弯管壁面磨损率的数值结果与Zeng等[20]采用电化学方法测量获得的试验结果对比如图1所示。由图1可知,沿着弯管曲率角逆时针方向,磨损率逐渐增加。弯管磨损率数值结果与试验结果吻合良好,最大磨损率与最大磨损位置预测准确。因此,该数学模型可以准确地预测液固两相流中壁面的磨损率与最大磨损位置。
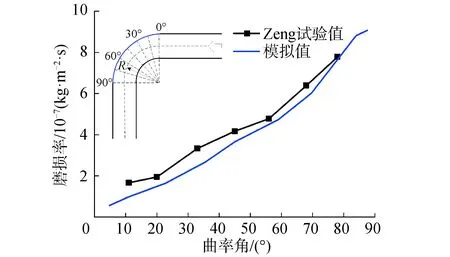
图1 弯管磨损率数值结果与试验结果对比Fig.1 Comparison of elbow erosion rate between numerical results and experimental data
2 模型泵及数值设定
2.1 模型泵及数值计算域
本文研究对象为单级单吸离心泵,主要几何参数如表2所示,其设计参数为:流量25 m3/h,扬程15 m,转速2 500 r/min,比转速135。数值计算域包括进口延伸段、叶轮、无叶扩压器、蜗壳及出口延伸段,其中进口延伸段长度为叶轮进口直径的3倍,出口延伸段长度为蜗壳出口直径的3倍。

表2 模型泵主要几何参数Table 2 Main geometric parameters of model pump
2.2 网格划分
为了生成高质量的网格,采用ICEM-CFD里的结构化六面体网格对数值计算域进行划分。为了准确地捕捉近壁面湍流,在近壁面采用加密处理,并调整第1层网格高度,将壁面y+值控制在30附近,最终的网格划分结果如图2所示。

图2 计算域网格划分Fig.2 Grid generation of computational domain
2.3 数值设定
数值计算时选取25°清水为连续相,球形沙颗粒(SiO2)为离散相。采用滑移网格技术模拟转子与定子间的相对运动,设置进口延伸段和扩散段与叶轮的交界面为滑移界面,叶轮计算域设在旋转坐标系,其余计算域设在静止坐标系。进口边界条件设为流体速度,出口边界条件设为自由出流。球形沙颗粒从进口处垂直于进口面恒定释放,速度与流体速度一致。非稳态计算时间步长设为0.000 1 s,即叶轮每旋转1.5°求解一次,每个时间步长迭代次数设为20次。
2.4 网格无关性验证
为了验证网格无关性,选取7组结构化六面体网格对数值计算域进行划分,并计算模型泵在设计工况下壁面的平均磨损率。平均磨损率随网格数变化趋势如图3所示。由图3可知,随着网格数增加,平均磨损率呈减小趋势,但当网格数增加至286万后,平均磨损率的变化很小,在5%范围内,因此,本文选取模型泵的计算网格数为286万。

图3 网格无关性研究设计工况Fig.3 Grid independence study
3 计算结果与分析
为了探索离心泵磨损初期各个区域的磨损形态和磨损率以及其受颗粒粒径及浓度的影响,本文对设计工况、不同颗粒粒径工况、不同颗粒浓度工况下的模型泵进行了研究。由于磨损初期壁面磨损较轻,壁面变化引起的通流型线变化较小,对磨损发生的情况和磨损条件的影响较小,因此,本文忽略通流型线的变化对磨损的影响。
文献[2]指出黄河砂中值粒径为30 μm,多砂河常见粒径为90 μm。虽然实际泵流动的两相流颗粒的直径不会是某一均匀直径,但采用平均粒径计算的结果与采用一定颗粒直径范围计算的结果差别很小。为了分析粒径对磨损形态和磨损率的影响,本文设计工况下选取平均粒径60 μm,选取颗粒浓度32 kg/m3;不同颗粒粒径工况时保持其他参数不变,颗粒直径设为30、90、120 μm;不同颗粒浓度工况时保持其他参数不变,颗粒浓度设为19.5、44.5、57 kg/m3;具体计算工况如表3所示。

表3 计算工况Table 3 Calculation conditions
3.1 设计工况下离心泵壁面的磨损特性
为了探索离心泵壁面的磨损特性,对设计工况下模型泵各个区域的磨损形态进行了预测并对比了不同区域的最大和平均磨损率,分析了叶片与后盖板交界处磨损率随叶片曲率角的变化规律并预测了最大磨损率发生位置。
图4为模型泵各个区域磨损形态的时间演化。由图4可知,与其他过流部件相比,蜗壳和出口延伸段的磨损较轻,叶轮的磨损较严重,尤其是叶片前缘及叶片压力侧尾缘附近区域。与叶轮前盖板相比,叶轮后盖板磨损区域面积更大。当磨损时间由0.5 s增至2.0 s,蜗壳及出口延伸段的磨损率变化较小,叶轮及扩压段的磨损率及磨损区域面积增加明显,尤其是叶片压力侧尾缘附近区域。叶片前缘的磨损区域面积增加不明显。当磨损时间为2 s时,前盖板靠近叶片压力侧尾缘区域、后盖板中部区域、后盖板外围区域均遭受了严重的磨损。
图5为不同区域的最大和平均磨损率对比图。由图5可知,最大磨损率最大值发生在叶片和后盖板区域,为7.9×10-4kg/m2;平均磨损率最大值发生在后盖板区域,为1.4×10-6kg/m2;最大和平均磨损率最小值均发生在进口延伸段,分别为1.0×10-8和 2.6×10-9kg/m2;最大和平均磨损率分布规律不一致,例如,前盖板的最大磨损率低于叶片,但平均磨损率高于叶片;同一区域的最大和平均磨损率差距巨大,例如,叶片的最大磨损率是平均磨损率的2 079倍。由以上分析可以推测,叶轮后盖板是磨损最严重的区域,最大磨损率发生在叶片与后盖板交界处。
图6为叶片与后盖板交界处磨损率随叶片曲率角的变化规律。由图6可知,叶片压力侧与吸力侧的磨损率随叶片曲率角的变化规律不同,叶片吸力侧的磨损率曲线较平缓,叶片压力侧的磨损率曲线波动较大,叶片前缘吸力侧的磨损率大于压力侧,叶片尾缘压力侧的磨损率大于吸力侧;但无论是叶片压力侧还是吸力侧,磨损率均是在叶片前缘取得最大值,最大磨损率发生在叶片曲率角59.8°附近,为7.9×10-4kg/m2。
3.2 颗粒粒径对叶轮磨损特性的影响
为了进一步探索离心泵壁面磨损特性的影响因素,对不同颗粒粒径工况下(工况1、2、3)离心泵的磨损率进行了计算。由上述分析可知,叶轮是离心泵内磨损最严重的过流部件,最大磨损率发生在叶片与后盖板交界处。因此,这里分析颗粒粒径对叶轮磨损形态及磨损率变化规律的影响,结果如图7、图8所示。图7为不同颗粒粒径工况叶轮磨损云图变化,其中左边为前盖板,中间为叶片,右边为后盖板。由图7可知,叶轮磨损形态受颗粒粒径影响显著。随着颗粒粒径的增大,磨损区域面积逐渐减小。这主要是由于在保持颗粒浓度不变的情况下,随着颗粒粒径的增大,颗粒数减小,叶轮壁面受到的撞击次数减小。当颗粒粒径为30 μm 时,叶轮前后盖板中部及外围均受到了不同程度的磨损,叶片前缘及叶片压力侧尾缘附近区域磨损严重;当颗粒粒径增大至90 μm 时,前盖板及叶片的磨损区域面积显著减小,而后盖板的磨损区域面积几乎不变,但同一位置的磨损率显著减小;当颗粒粒径增大至120 μm 时,前盖板的磨损区域只有叶片压力侧尾缘附近区域,后盖板的磨损区域仍然是中部及外围。
图8为不同颗粒粒径工况叶片与后盖板交界处磨损率随叶片曲率角的变化规律。其中,图8(a)为叶片压力侧,叶片曲率角在-22.5°~59.8 °变化;图8(b)为叶片吸力侧,叶片曲率角在-32.5°~59.8°变化。由图8(a)可知,在各个粒径工况下,叶片压力侧磨损率基本是随叶片曲率角先减小后增大,最大峰值在叶片曲率角59.8°附近,第2峰值在叶片曲率角-22.5°附近;由图8(b)可知,在各个粒径工况下,叶片吸力侧磨损率基本是随叶片曲率角先小幅度变化到叶片曲率角55°附近迅速上升,在叶片曲率角59.8°附近达到最大值;随着颗粒粒径增大,叶片压力侧及吸力侧磨损率总体上呈减小趋势。

图4 磨损形态的时间演化Fig.4 Time evolution of erosion pattern

图5 设计工况t=10 s时不同区域的最大和平均磨损率对比Fig.5 Comparisons of the maximum and average erosion rates for different regions under design condition at t=10 s
3.3 颗粒浓度对叶轮磨损特性的影响
为了进一步探索离心泵壁面磨损特性的影响因素,对不同颗粒浓度工况下(工况4、5、6)离心泵的磨损率进行了计算并分析颗粒浓度对叶轮磨损形态及磨损率变化规律的影响,结果如图9、图10所示。图9为不同颗粒浓度工况叶轮磨损云图变化,其中左边为前盖板,中间为叶片,右边为后盖板。由图9可知,叶轮磨损形态受颗粒浓度影响显著。随着颗粒浓度的增大,同一位置的磨损率显著增大。这主要是由于在保持颗粒粒径不变的情况下,随着颗粒浓度的增大,颗粒数增大,叶轮壁面受到的撞击次数增多。但叶轮各个部分的磨损区域面积几乎不变,这说明改变颗粒浓度,不会改变颗粒撞击角。当颗粒浓度为19.5 kg/m3时,严重磨损主要集中在叶片前缘附近区域;当颗粒浓度增大至44.5 kg/m3时,同一位置的磨损率增大,叶片压力侧尾缘附近变成严重磨损区域;当颗粒浓度增大至57 kg/m3时,同一位置的磨损率进一步增大,叶片压力侧尾缘附近严重磨损区域面积增加明显,叶片前缘附近严重磨损区域面积变化较小。
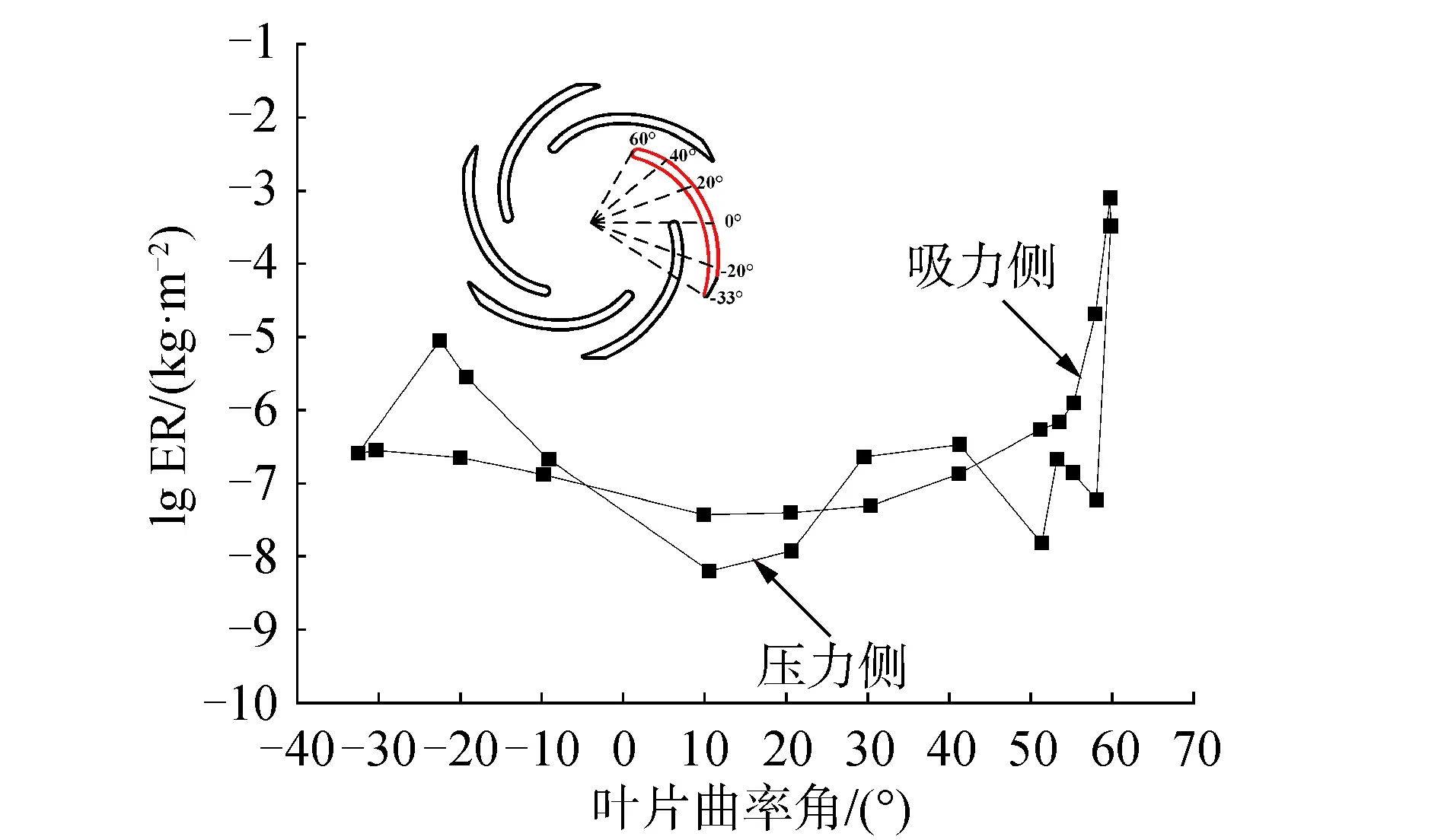
图6 磨损率随叶片曲率角的变化规律(dp=60 μm,Cm=32 kg/m3)Fig.6 Variation of the erosion rate along the blade curvature angle(dp=60 μm,Cm=32 kg/m3)

图7 不同颗粒粒径叶轮磨损云图Fig.7 Impeller erosion contours for different particle diameters
图10为不同颗粒浓度工况叶片与后盖板交界处磨损率随叶片曲率角的变化规律。其中,图10(a)为叶片压力侧,叶片曲率角在-22.5°~59.8°变化;图10(b)为叶片吸力侧,叶片曲率角在-32.5°~59.8°变化。由图10(a)可知,在各个浓度工况下,叶片压力侧磨损率的分布基本上是叶片前缘尾缘大,中间区域小,在叶片曲率角59.8°附近达到最大值,在叶片曲率角-22.5°附近达到第2峰值;由图10(b)可知,在各个浓度工况下,叶片吸力侧磨损率的分布基本上是叶片前缘大其余区域小,也是在叶片曲率角59.8°附近达到最大值;随着颗粒浓度增大,叶片压力侧及吸力侧磨损率随叶片曲率角的变化规律较一致,同一位置上的磨损率基本上呈增大趋势。

图8 不同颗粒粒径下磨损率随叶片曲率角的变化Fig.8 Variations of the erosion rates along the blade curvature angle for different particle diameters
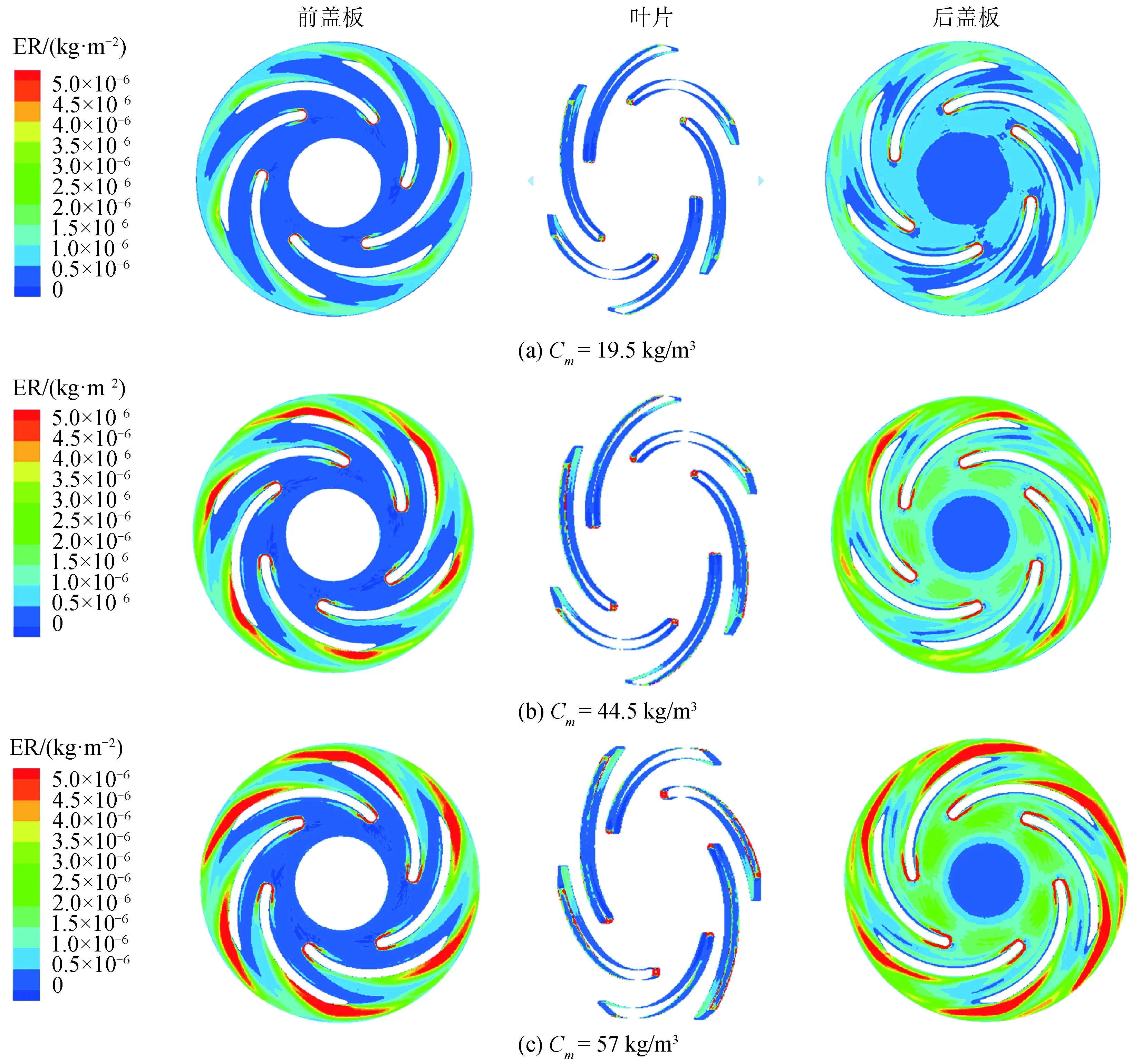
图9 不同颗粒浓度叶轮磨损云图Fig.9 Impeller erosion contours for different particle concentrations

图10 不同颗粒浓度下磨损率随叶片曲率角的变化Fig.10 Variations of the erosion rates along the blade curvature angle for different particle concentrations
4 结论
1) 叶轮是离心泵内磨损最严重的过流部件,最严重的磨损发生在叶片前缘及叶片压力侧尾缘附近区域。
2) 进口延伸段的最大和平均磨损率小于其它区域,叶片和后盖板的最大磨损率大于其它区域,叶片与后盖板交界处叶片曲率角59.8°附近的最大磨损率达到最大值。
3) 前盖板及叶片的磨损区域面积随粒径增大显著减小,而后盖板的磨损区域面积随粒径增大几乎不变,同一位置的磨损率随粒径增大呈减小趋势。
4) 叶轮各个部分的磨损区域面积随浓度增大几乎不变,同一位置的磨损率随浓度增大呈增大趋势,叶片压力侧及吸力侧磨损率随浓度增大变化规律较一致。
