应用Stokes矢量的水下探测增强算法

许志成

(黎明职业大学 信息与电子工程学院，福建 泉州 362000)

1 引 言

水下成像作为一种重要的探测技术，在各种工程领域都得到了广泛的应用[1]。随着越来越多的水下设施的建设与应用，水下探测技术也显得越来越重要。海底资源开采、海底电缆、管道布置，海洋生物研究等等都离不开水下探测技术的使用[2-4]。然而，由于水下环境相比较于地面环境更加复杂，不可控因素较多等原因，使得水下成像探测技术的应用受到了很多限制[5]。其主要表现在水中杂质的存在导致水下成像不清晰。由于水中存在着大量的微生物以及固体颗粒等各种散射介质，这些散射介质的存在影响了光的直线传播，在光的传播方向上引入了大量的噪声，因此，最终便导致了水下探测目标成像模糊不清晰等问题，水域的浑浊度越大，其影响也越严重。解决因散射问题而带来的噪声干扰已成为水下探测技术研究所必须解决的重大问题[6]。

基于散射理论与光的大气传输模型，人们很早就开始了探测增强技术的研究。对于地面上的探测增强技术，主要有图像增强技术和基于物理模型的图像复原技术两种。在地面探测中，雾、霾等散射介质是主要的噪声干扰。图像增强技术的基本原理是通过对图像中的参数、属性进行调整以提高原始图像的对比度，使其能相对于原始图像具有更高的辨识度。2015年，唐美玲等[7]提出了一种基于图像熵与平均灰度的自适应中值滤波算法，该算法能够使处理后的图像拥有较好的视觉效果，对比度、亮度均有较为显著的提高。而图像复原技术的基本原理是基于光传播散射原理构建图像的形成模型，通过求解模型中的目标原始图像值从而达到将模糊图像“复原”的目的。2009年，He等[8]提出基于暗通道先验理论的图像去雾算法，该算法通过暗通道先验理论估算雾图形成模型中的未知参数值来求解目标图像，来达到“去雾”的目的。后续学者提出的许多算法都是在该算法的基础上进行改进的。目前的水下探测目标增强主要是通过图像融合匹配增强和水下传输模型解算来实现的[9]。2016年，马硕[10]提出了一种基于前景模型解算的水下图像增强算法，该算法利用光强在水中的衰减特性，推导出光波长与散射系数的关系，通过该关系实现对图像的通道增益，该算法能在一定程度上降低图像模糊和颜色失真效应，改善水下成像过曝的问题。2018年，冯辉等[11]提出一种基于直方图均衡化的水下图像增强算法，通过原始图像的直方图进行均衡化处理，从而提升图像的对比度。2019年，高雅昆[12]提出一种基于立体算法的图像匹配技术，该算法通过对同一场景的多张图片进行对比结合解算，能够有效提高图片的对比度，降低图像颜色失真。偏振差分增强技术主要是应用在水下偏振成像上，其通过对两幅相互正交的偏振图像作差分计算的方式来实现图像显示增强的效果。

目前而言，无论是多张图片的融合处理技术和水下传输模型解算技术都是基于强度与波长这两个维度的信息处理来实现的，但是在水体环境下，这两个维度信息的变化具有很强的随机性和任意性。基于光强和波长信息进行成像虽然能在一定程度上改善目标图像的显示质量，却难以达到目标复原的效果。光的偏振特性是一种受水体散射影响较小，变化规律可循性较高的光维度信息。本文基于光传输与散射模型建立水下图像形成模型，通过偏振光理论求解模型中的原始图像，以实现低成本、有效的水下图像复原，达到探测增强的效果。

2 Stokes矢量及探测增强算法

2.1 Stokes矢量

偏振是光的一种独立属性，用于描述光波在振动平面上的倾向性。由于光在与介质作用发生散射现象时会伴随着偏振态的变化，因此通过对散射现象的偏振信息进行分析，能够为成像模型求解提供有力的工具与手段。偏振态是完全独立于光强的信息，任何光的偏振态都可以用Stokes矢量完全地表示，Stokes矢量是个思维向量，由4个分量构成。如式(1)所示。

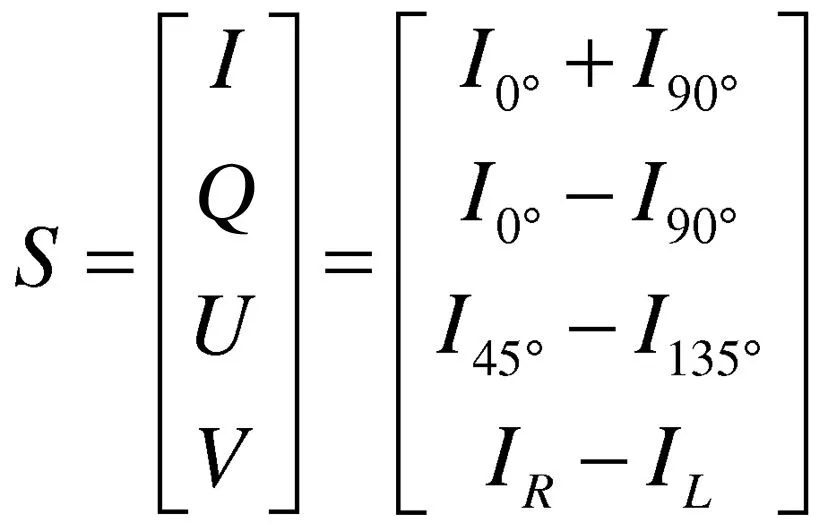
(1)

其中：I表示光波的总光强，其数值大小等于两个相互垂直的偏振光强之和；Q表示水平方向偏振光强与垂直方向偏振光强的差值；U表示45°方向的偏振光强与135°方向偏振光光强的差值；V表示右旋偏振光强与左旋偏振光强的差值。文中由于不涉及圆偏振分量的测量与求解，因此可以将Stokes矢量简化为三维的情况。

Stokes矢量的测量通过在探测器前安装不同偏转角度的偏振器来实现。经过偏振器后的光强与偏振器的偏振角度有如下关系。

(2)

式(2)包含3个未知参数的函数关系式，这些未知参量恰好是Stokes矢量的前3个参量。因此只要取3个角度值测量其透过光强，便可以建立方程组将Stokes分量求解出来。

2.2 探测增强算法

探测器所探测到的图像可由式(3)描述，其中I表示探测器接收到的总光强，D表示场景的正投射光强，A表示因散射而产生的杂散光。即有

I=D+A

(3)

场景正投射光与杂散光都是和透射率有关的函数，透射率是一个随距离衰减的函数，场景透射光强随透射率的减少而减少，杂散光强随透射率的增加而增加。场景正投射光强和杂散光同透射率之间的关系，可分别由式(4)，式(5)表示，其中t表示透射率，J表示场景的原始光强。它是我们最终要求的目标值，A′是个极限量，它表示距离探测器无穷远的杂散光强值。

D=Jt

(4)

A=A′(1-t)

(5)

联立(3)、(4)、(5)式，消去透射率t，可以得到场景原始光强J的求解式为

(6)

通过对式(6)进行求解，便能够实现图像复原的目的。在该式中，总光强值I是探测器直接获取的，因此本算法最关键的技术在于A和A′的求解。

如式(3)所示，总光强是由场景透射光以及杂散光叠加而成的。其中，场景透射光是目标物体所反射的光，其反射光的偏振度极低，在此将其偏振度忽略，当作非偏振光处理；而杂散光A是由散射现象所产生的，如上文所述，散射会导致光波的偏振态发生变化，便使得杂散光A成为具有一定偏振度的部分偏振光。

若改变放置在探测器前的偏振器转角，则探测器所接收到的光强会发生变化，而这部分随偏振器转角而变化的光强完全来自于杂散光A的偏振光分量。通过选取3个不同的偏振器转角值，可以获取3组角度与光强对应的关系值，在此选择0°、45°、90° 3个值进行计算，构建式(7)的方程组，可求解出每个像素点所对应的Stokes矢量。

(7)

由此，式(2)函数关系式中的各个参数值便能被完全地确定下来。对于一个连续、区间有界的函数必定存在最大值和最小值，其光强的最大值与最小值之差即为杂散光A中的偏振光分量的光强。对于光强的最大值与最小值，可通过求解函数的一阶导数与二阶导数获得，将杂散光中的偏振光分量用Ap表示，通过联立式(8)、(9)式将其求解。

(8)

Imax=(θ1),Imin=(θ2)

Ap=Imax-Imin

(9)

上文中提到探测器所接受的光强值是场景与杂散光两种光强的叠加，但这只是对于接收到场景反射光的像素点而言，没有接收到场景反射光的像素点时，其接收到的光强便全为杂散光。由于场景反射光是非偏振光，而杂散光是部分偏振光，因此，对于像素点而言，其总光强中场景反射光的占比越高，该像素点的偏振度便越小；反之，其偏振度则越大。对只包含杂散光的像素点而言，其偏振度是最大的。因此，可根据式(10)计算探测器中每个像素点的偏振度值，选取其中最大的偏振度作为杂散光的偏振度。将杂散光的偏振度标记为pmax，每个像素点中的杂散光光强值A可通过式(11)求解得出。

(10)

(11)

对于A′而言，可以采用最值法进行估算求解，探测器中的每一个像素的光强值组成都可以由式(3)表示。如上文所述，场景散射光的光强值随探测器与场景的增加而减小，而杂散光强值则随距离的增加而增加。当距离为无穷远时，像素点中光强值即为无穷远处的光强值，其光强达到最大值，并且因为其光强全为杂散光，其偏振度也达到最大值。故对于A′可以通过以下方式近似求解：求解探测器中每一个像素点的偏振度值，按从小到大的顺序选取偏振度前0.1%的像素点；在这些像素点中进行二次选取，选取其中的最大的光强值作为A′的值。由此，A和A′全部求解后，可通过式(6)将最终的原始目标场景光强值求出。

3 实验测试

为了验证算法的有效性，进行实验测试。测试的物体为一个圆形罐状包装物，为了进行测试，需要创造水体散射环境。放置水体的容器为内边长为1 m的透明玻璃正方体容器，将待测物放入该容器中，并在容器中添加天然浑浊水体。本实验所使用的水体环境为含杂量不同的江水。在距离被测试物70 cm的前方处放置相机，进行图像采集与探测。一切实验设备搭建完成后，对目标物进行图像采集，然后采用本文所提出的算法对图像进行处理。

实验中，通过计算还原后图像与原始图像目标区域相对相关系数来衡量图像还原效果。当相关系数达到0.7时，图像的大多数细节都能被保留下来，此时可认为图像具有较好的还原效果。本实验中选取了含杂量依次递增的5个水体环境进行实验，实验结果如表1所示。

表1 不同含杂量水体环境下的图像复原结果

可以看到在水体的含杂量不超过8 kg·m-3时，图像相关系数都达到了0.7以上，图像具有较佳的还原效果；而含杂量达到10 kg·m-3时，相关系数小于0.7，图像出现了较为明显的失真。

对于天然的不受污染的水体而言，其含杂量一般小于4 kg·m-3，因此含杂量4 kg·m-3的实验组能代表大多数无污染水体下的成像情况。该组实验的图像处理结果如图1所示。

(a)算法处理前的图像 (b)算法处理后的图像

通过对比可以看出，处理后图像清晰度比处理前的图像有较大改善。在图1(a)中，因水体散射的问题，造成多处过量曝光，散射所产生的杂散光严重干扰了目标物体的反射光强，图像的可识别度较差。通过本文算法进行处理后，原图像中的大部分杂散光都被移除了，此时图像的清晰度和对比度有了很大的提高。被探测物上的大多数细节也变得清晰可见，被探测物上的图案以及文字都明显呈现了出来，使得图像具备了较高的可识别度。

4 结束语

本文针对因水体散射造成的水下探测噪声干扰问题，提出一种基于偏振光理论的图像复原增强算法。该算法通过采集探测图像偏振信息并结合偏振与散射关系来实现图像复原的目的。经实验测试表明，该算法在含杂量不大于4 kg·m-3，不受污染水体环境下具有较强的图像还原增强效果；对于水体环境受较轻污染，含杂量小于8 kg·m-3的水体环境下，该算法也同样具有可用性。