非单调线性互补问题的宽邻域算法复杂度分析

赵花丽

(咸阳师范学院数学与信息科学学院，陕西 咸阳 712000)

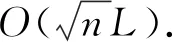
1 宽邻域不可行内点算法

考虑P*(κ)线性互补问题：求(x，s)∈n×n使得

xTs=0，s=Mx+q， (x，s)≥0

，

其中q∈n，矩阵M∈n×n是P*(κ)矩阵，即记解集F*={(x*，s*)∈F|x*Ts*=0}，可行集F={(x，s)∈n×n|s=Mx+q，(x，s)≥0}.假定迭代点位于下面的邻域内

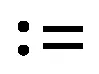
方向(Δx1，Δs1)和(Δx2，Δs2)可分别由下面线性系统解得

(1)

(2)

记

Δx3=λΔx1+(1-λ)Δx2， Δs3=λΔs1+(1-λ)Δs2

，

(3)

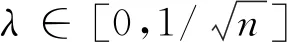
λ=max{λ：f(λ)=(Δx3)TΔs3+(1+3κ)(1+γτ)nμ≥0}

.

(4)

给定步长α>0，则新的迭代点为

x(α)=x+αΔx3=x+αλΔx1+α(1-λ)Δx2

，

(5)

s(α)=s+αΔs3=s+αλΔs1+α(1-λ)Δs2.

(6)

令η=1-αλ，则残差可表示为r(α)=s(α)-Mx(α)-q=ηr.

算法1：

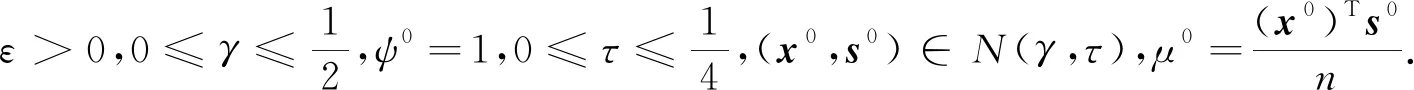
步1 如果ψk≤ε，停止.

步2 由式(1)～(2)分别计算(Δx1，Δs1)和(Δx2，Δs2)，由式(3)～(4)计算λk及(Δx3，Δs3).

步3 选择αk∈[0，1]满足μ(αk)≤μk和(x(αk)，s(αk))∈N(γ，τ).令ηk=1-λkαk.由式(5)～(6)计算(x(αk)，s(αk)).

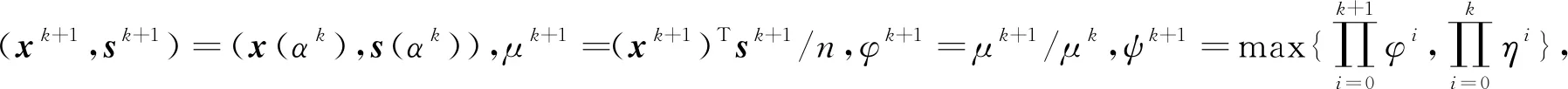
注1在算法1中，取初始点x0=s0=ηe，其中η>0满足ηe-(x0+s0)≥0.

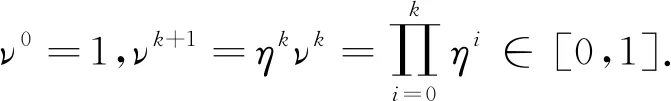
2 算法复杂度分析

引理1[8]对P*(k)线性互补问题，z=(x，s)∈n，线性系统有唯一解(u，v)满足+3ζ(z，b))，其中

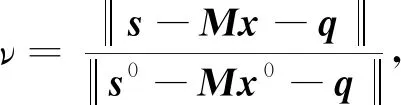
引理3设(x*，s*)∈F*，(x0，s0)∈N(γ，τ)，{(x，s)}是算法1产生的序列，则

证明：由Mx*-s*=-q有M(λν(x*-x0))-λν(s*-s0)=λνr0=λr，则

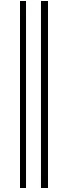
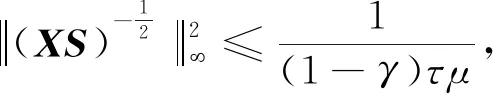
证毕.

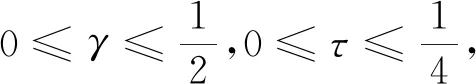
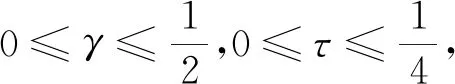
证明：由引理1和引理3、引理4有

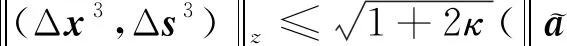
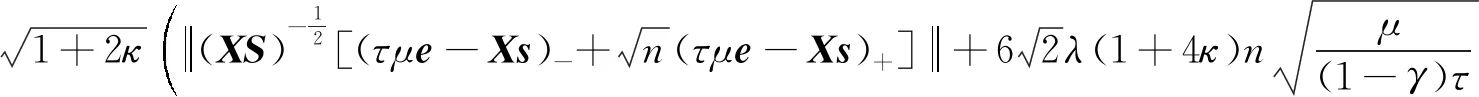
因为

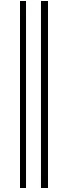
所以

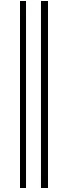
又因为

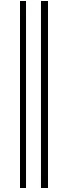
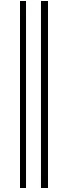
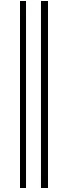
类似于引理5的证明有下面引理：

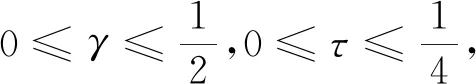
(Δx2)TΔs2≥-κnμ(1+γτ)，

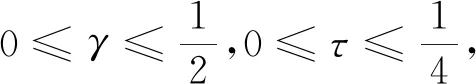
证明：由式(5)和引理6有

f(λ)=λ2(Δx1)TΔs1+λ(1-λ)((Δx1)TΔs2+(Δx2)TΔs1)+(1-λ)2(Δx2)TΔs2+(1+3κ)(1+γτ)nμ≥

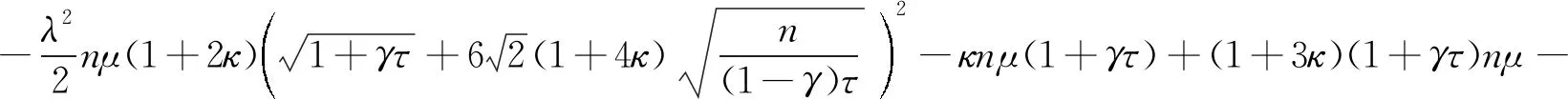
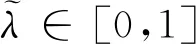
因此有

证毕.

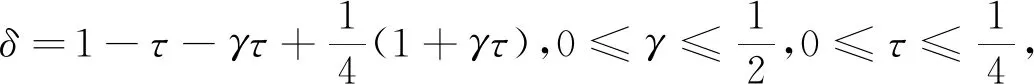
证明：因为

x(α)Ts(α)=(x+αΔx3)T(s+αΔs3)=

利用Cauchy-Schwartz不等式有

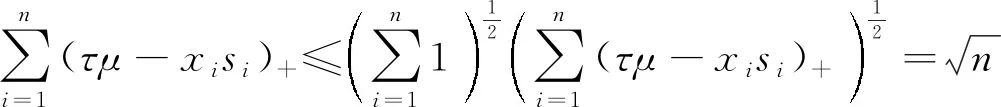
进一步有

又因为

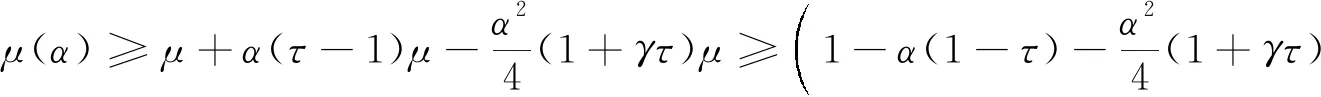
所以

证毕.

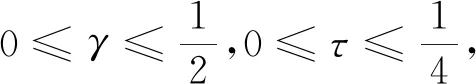
证明：因为

所以μ(α)关于α∈[0，1]是单调递减的.证毕.

定义

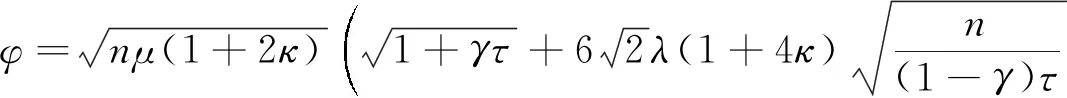
类似于文献[6]中引理5.8和5.9的证明，易得下面两个引理：

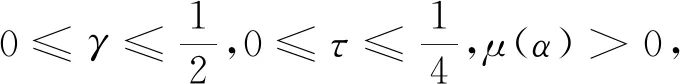
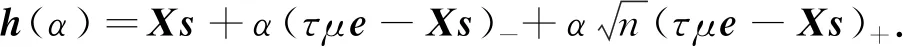
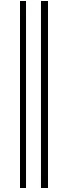
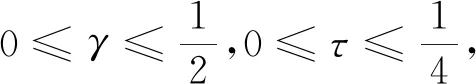
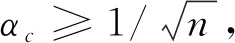
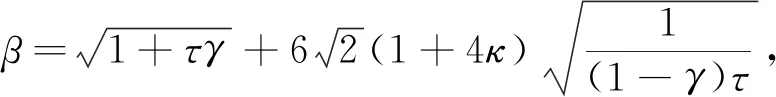
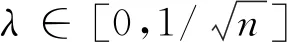
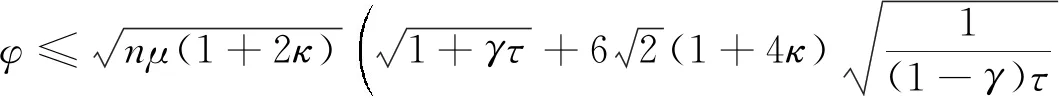
所以

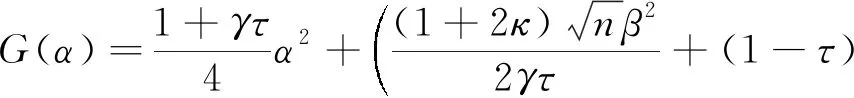
为了获得T(α)≤0的最大值α，只需求得G(α)≤0的最大值α即可.我们考虑G(α)的正根α+.因为

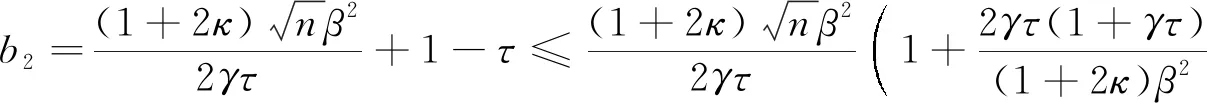
及

所以有

又因为

所以

因此

证毕.

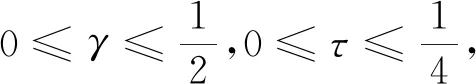
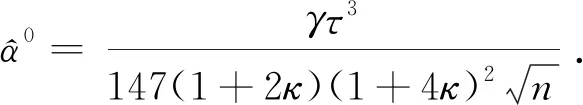
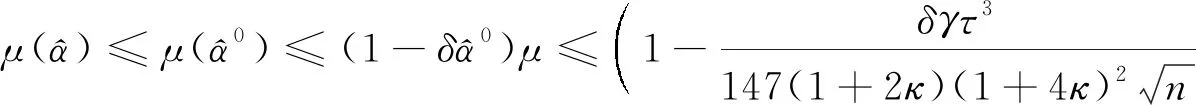
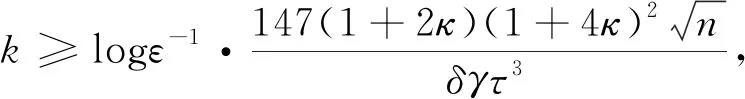
又因为

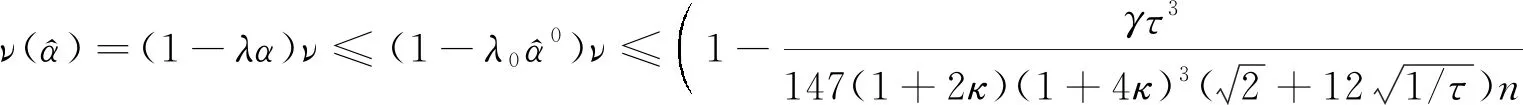
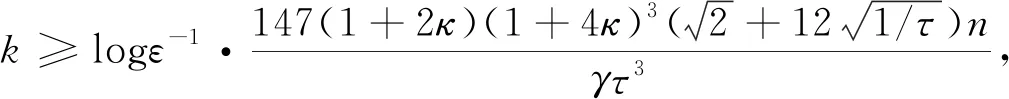
成立，这就意味着ν≤ε.

因此算法最多O((1+2κ)(1+4κ)3nlogε-1)步终止.证毕.

3 数值实验

在这里我们利用三个算例测试算法1，见例1～例3.取参数γ=0.5，τ=0.05，λ=0.89，算法的终止条件为max{r，mu}≤10-6；用k表示算法的迭代步数，t表示算法的运行时间.数值实验结果见表1.由表1可见，算法1的迭代步数和计算时间都优于文献[7]的算法1.

例1取

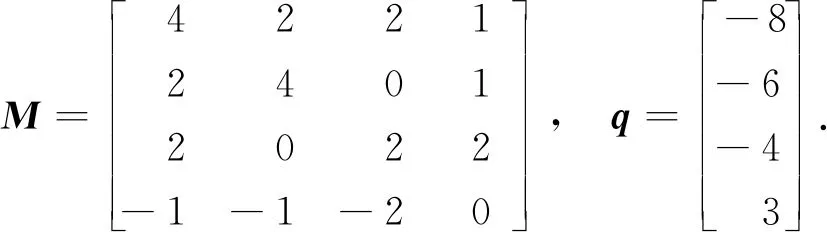
例2取

例3取

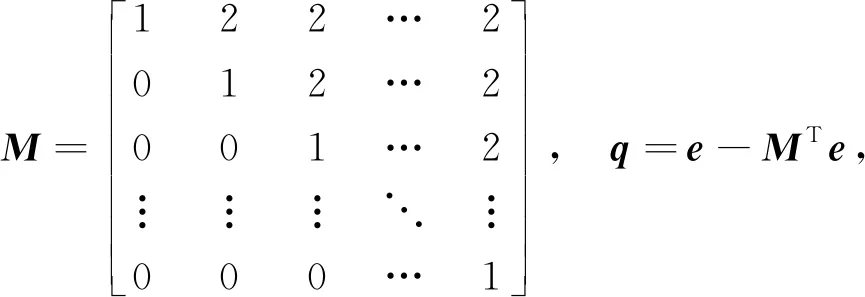
表1 非单调线性互补问题的数值结果

4 小 结

针对P*(κ)线性互补问题，本文研究了宽邻域不可行内点算法，该算法的复杂度与当前最好的复杂度一致.同时利用三个算例测试了算法的实际计算效果，从数值结果看，该算法无论是迭代次数还是计算时间都是有优势的.