圆盘剪剪切废边运动轨迹的计算与模拟

冀俊杰，李 菲，谭 进，张 镭

(中国重型机械研究院股份公司，陕西 西安 710032)

0 前言

20世纪70年代由于计算机和数值计算技术的发展，一些学者将其引入到切削加工领域，形成了切削加工仿真技术。以计算机为工具, 采用商业有限元软件来模拟切削过程，已成为金属切削研究领域的热门方向。有限元模拟不但能节省大量的人力和物力, 还可以得出许多从实验中难以测量的重要数据，仿真结果形象、直观，对实践有着很高的指导价值。

被圆盘剪切除的废边运动轨迹在实际工程中也是一个关注的重点，由于圆盘剪运行速度越来越快，如果溜槽轨迹与废边运行轨迹不能够吻合，容易造成卡阻等现象，影响圆盘剪运行及带来机组停产。

对于圆盘剪剪切后的废边，由于剪切材料厚度、宽度、剪切速度、重叠量和侧向间隙大小的不同，所形成的曲线不尽相同。通过数值分析的方法可得到不同废边曲线，这可为溜槽设计提供有效的数据信息。

以切削速度、带钢厚度、废边宽度为变量，通过控制变量法，计算并模拟带钢被切除后废边的运动轨迹，得到了在一定条件下剪切一瞬间被切除废边的运动轨迹与切削速度、带钢厚度、废边宽度的关系。

1 剪切过程分析

圆盘剪对带钢的剪切过程由压入变形和剪切滑移两个阶段组成，剪切过程的实质是金属塑性变形的过程。剪切时，圆盘剪刀盘相对于带钢的运动速度做圆周运动，形成一对重叠的剪刃。板带剪切过程是：随着刀盘的不断转动，带钢与上下刀盘距离逐渐减小，中间的带钢被刀轴不断地切入，使带钢材料发生变形，最终被完全切断的过程，如图1所示。

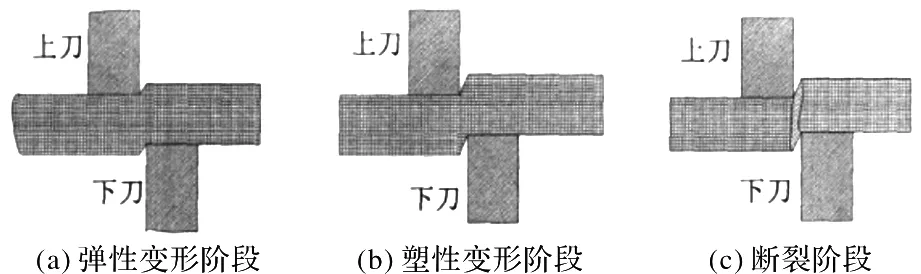
图1 带钢被剪切过程

(1) 弹性变形阶段。上下刀盘与带钢接触并挤压，带钢产生弹性压缩。随着带钢与刀盘之间距离的不断减小，带钢变形愈加严重，此时应力未超过弹性极限，一旦上下刀分离，则板带可恢复原形。

(2)塑性变形阶段。随着带钢与刀盘之间距离的不断减小，带钢变形达到它的屈服极限。部分材料被刀侧面挤压产生塑性变形，得到光亮的剪切断面。由于侧隙的存在，塑性变形的同时还伴有材料的弯曲与拉伸。剪切继续进行，材料内应力不断增大，在刀刃口处由于应力集中，此处的最大应力状态超过材料的断裂极限，开始出现微小裂纹。

(3)断裂阶段。随着上下刀盘切入材料的深入，刃口处的裂纹不断向材料内部扩展，上下裂纹相互重合材料随即断开。

塑性应变只出现在剪切区范围内，在钢板边部和中心是没有塑性变形的。最大的塑性应变为0.098 99，根据被剪切材料的模型，当塑性应变达到0.1，钢板就会断裂，单元就会被删除。钢板在剪切线附近产生比较大的塑性应变,而离剪切线较远的部位不发生塑性应变,在距离剪缝40 mm处塑性应变值为0,没有产生塑性应变。

2 建立参数表

废边的运动曲线主要受废边的宽度、厚度、运行速度及圆盘剪的重叠量、侧向间隙大小的影响，并在不同时长内带钢质量及悬垂长度对曲线的影响会有所不同。在此仅分析有限时间(即剪切瞬间)、有限长度内，圆盘剪的重叠量、侧向间隙大小对断面质量和剪切效果的影响，确定不同厚度带材的重叠量和侧向间隙。选取代表性的带材厚度、宽度、速度进行分析，通过控制变量法，分别研究废边曲线与其宽度、厚度及运行速度的关系，最后根据机组曲线及数据归纳出一种近似曲线。主要参数表见表1、2、3所示。

表1 废边曲线随其厚度变化研究

表2 废边曲线随其宽度变化研究

表3 废边曲线随其运行速度变化研究

3 动力学分析

针对不同的参数，应用ANSYS/LS_DYNA有限元数值模拟软件建立模型，进行动力学分析，得到剪切瞬间的废边曲线。

3.1 参数设置

依据实际的剪切情况，刀盘采用各向同性弹性材料模型，钢板采用塑性随动强化模型，数值仿真参数表4所示。

表4 数值仿真参数

钢板材料参数:

密度/t·m37.85e-9

弹性模量/MPa 2.06e5

切线模量/MPa 584

泊松比 0.261

屈服应力/MPa 260

强化模型系数 1

等效塑性应变 0.1

应变速率C40

影响系数P5

刀片材料参数:

密度/t·m37.86e-9

弹性模量/MPa 2.10e5

泊松比 0.3

计算时电机动力转化为恒定转速施加到上、下刀轴的传动部分，上、下刀轴的传动部分施加绕x轴的转速，在钢板上施加600 m/min的初始速度。

3.2 有限元模型建立

(1)对剪切模型进行几何建模。由于剪切过程复杂，因此有必要对剪切模型进行简化。根据研究的目的，建模时只需建立轴系和被剪切板，对于轴系约束所有的平动自由度和x、y方向上的转动自由度，仅保留z方向上的转动自由度，钢板一侧施加对称约束，保留x方向自由度。如图2所示。

图2 简化几何模型

(2)对剪切模型进行网格划分。为便于网格划分,建模时对刀盘进行布尔操作,采用扫掠网格划分。单元属性的定义包括单元类型和材料模型,在网格划分后分别定义模型中各部分的单元属性,以便在生成PART时各组成部分可以生成不同的PART,以进行接触分析,接触边界通过设置接触类型和摩擦系数,靠PART自动识别。各接触部件之间的接触类型设置为自动面面接触。模型中有两对接触，分别是钢板与上剪盘接触、钢板与下剪盘接触。这里采用的是自动面面接触。有限元模型如图3所示。

图3 有限元模型

3.3 边界条件

带钢与上下刀盘的接触为刚体与变形体的接触，设置其接触方式为侵蚀面-面接触(ESTS)。带钢与上、下刀盘的静摩擦系数为0.15，动摩擦系数为0.1。根据实际情况，给上、下刀盘施加绕旋转轴的旋转载荷，并施加于转速相同的初始转速，给带钢施加与刀盘相对应的水平初速度和重力，并施加对称约束。

3.4 断裂准则

断裂准则的选取是研究钢板剪切加工的关键问题，剪切加工由于包括断裂过程而变的非常复杂，剪切模拟的重点主要是建立合理的模型来模拟材料剪切断裂的过程。数值模拟采用了Cockroft&Lathem 准则，该准则是基于应力、应变的累计破坏计算材料的弹塑性行为，根据材料的最大破坏值是否达到了临界值来判断材料的断裂与否，临界值虽然会受到加工条件的影响，但还是将其视为像强度极限、屈服应力一样的材料常数。

3.5 计算结果

鉴于计算机能力情况，本文仅分析剪切时一瞬间时长内的状况，计算结果不代表长时间生产过程的最终形态。

图4为圆盘剪切的初始状态，即0时刻的状态图，此时，带钢与上、下刀盘并未接触，图5为0.063 s时刻剪切过程的运动情况，图6为0.063 s时刻剪切过程的运动情况。

图4 0 s带钢被剪切时的状态

图5 0.02 s时带钢被剪切时的状态

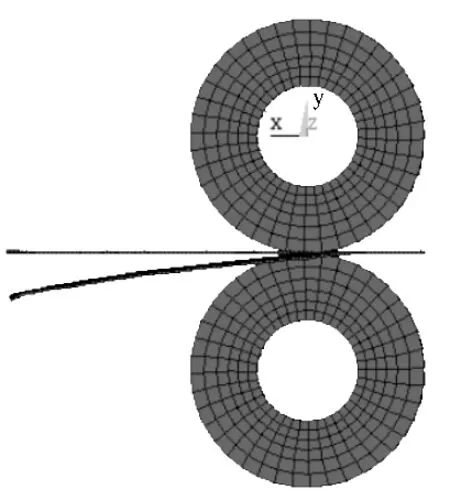
图6 0.04 s时带钢被剪切时的状态

图7为剪切过程中带钢y方向的变形云图。可以看出，带钢被剪切部分y方向的位移逐渐增大，端部变形最大，废边整体形状呈曲线。

图7 带钢y方向的变形云图

图8为钢板剪切时的Mises应力图,由图中可以看出,钢板剪切区产生的应力最大,最大应力出现在剪缝处而离剪切区域较远部位产生的应力较小,且钢板剪切过程中,与剪切区处在同一位置的钢板产生了比较大的弯曲应力,这与钢板实际剪切过程中的应力状态一致。

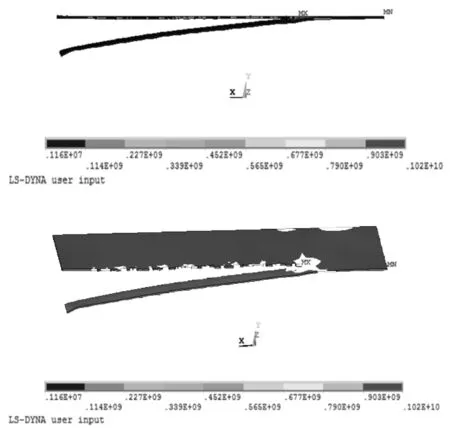
图8 钢板Mises应力图

4 函数化图形及曲线的选择

将提取的轨迹数据进行分析处理，得到抛物线的弧度及起始位置。在此考虑工程中的应用工况，抛物线的最高点是需要考虑溜槽的，否则带材会碰到溜槽上壁产生卡阻。同时考虑抛物线与水平面的最小夹角以及所剪切带材与数据表中最接近的曲线，根据实际工况中要求，选择并优化曲线作为溜槽的加工曲线。

(1)废边轨迹与带钢厚度的关系。取废边宽度为30 mm，圆盘剪切机运行速度为600 m/min，改变带钢的厚度，得到不同厚度带钢的废边轨迹，如图9所示，随着带钢厚度的增大，废边变形越大。

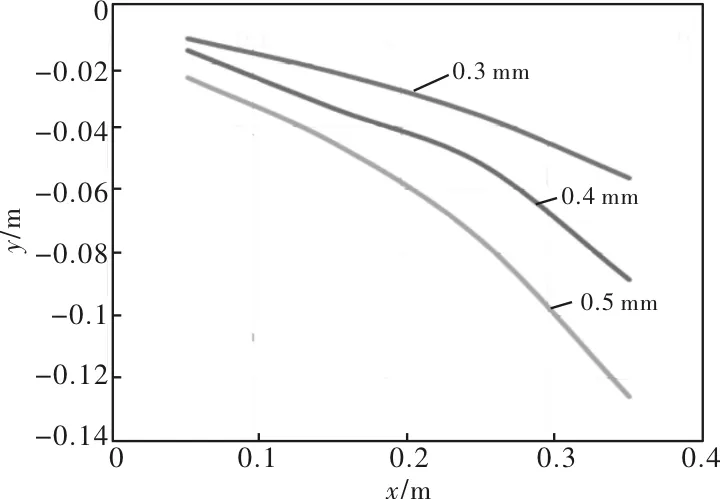
图9 废边轨迹与带钢厚度的关系

在此过程中，带钢越厚，废边所受剪切力越大，初始角度越大，变形越大，轨迹倾斜越明显。

根据实际中带钢的轨迹形状，可将其近视的看作二次曲线，通过拟合可以得到：当废边宽度为30 mm，圆盘剪运行速度为600 m/min时，不同厚度带钢废边的二次曲线。

0.3 mm厚带钢的废边对应二次曲线为

y=-0.221x2-0.055x-0.008=-0.221(x+0.125)2-0.00456

0.4 mm厚带钢的废边对应二次曲线为

y=-0.451x2-0.051x-0.012=-0.451(x+0.0567)2-0.01

0.5 mm厚带钢的废边对应二次曲线为

y=-0.715x2-0.043x-0.02=-0.715(x+0.03)2-0.02

不同厚度带钢的废边轨迹曲线与拟合的二次曲线如图10所示。

图10 不同厚度带钢的废边轨迹曲线与拟合的二次曲线

以废边轨迹的倾斜程度、顶点位置为参考，将不同厚度带钢的废边轨迹拟合成一条曲线为

(1)

式中，t为带钢厚度，mm；x、y为轨迹横、纵坐标，m。

(2)废边轨迹与圆盘剪剪切转速的关系。取废边宽度为30 mm，废边厚度0.3 mm，改变圆盘剪运行速度，得到圆盘剪在不同转速下废边的轨迹，如图11所示，从图中可以看出，随着圆盘剪转速的提高，废边变形越大。

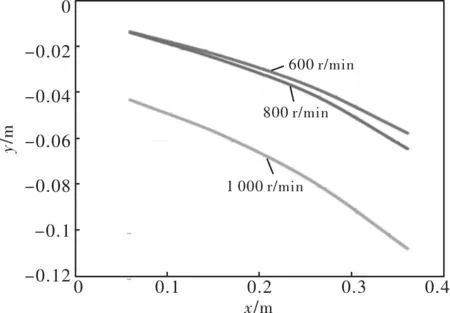
图11 废边轨迹与转速的关系

在此过程中，带钢所受的剪切力相同，而速度越大造成的冲击力越大，初始角度越大，轨迹倾斜越明显。

通过拟合可以得到：当废边宽度为30 mm，废边厚度为0.3 mm时，不同圆盘剪转速下，带钢废边的二次曲线。

600 m/min转速下带钢的废边对应二次曲线为

y=-0.221x2-0.055x-0.008=-0.221(x+0.125)2-0.00456

800 m/min转速下带钢的废边对应二次曲线为

y=-0.272x2-0.055x-0.009=-0.272(x+0.1)2-0.0063

1000 m/min转速下带钢的废边对应二次曲线为

y=-0.33x2-0.079x-0.036=-0.33(x+0.12)2-0.03

圆盘剪不同转速下，废边轨迹曲线与拟合的二次曲线如图12所示。

图12 不同速度废边轨迹曲线与拟合的二次曲线

以废边轨迹的倾斜程度、顶点位置为参考，将不同圆盘剪转速下带钢的废边轨迹拟合成一条曲线为

y=-0.0013v0.8(x+0.12)2-2.4×10-13v3.7

(2)

式中，v为圆盘剪转速，m/min。

(3)废边轨迹与废边宽度的关系。取废边厚度0.3 mm，圆盘剪切机运行速度600 r/min，改变废边宽度，得到不同废边宽度下的废边轨迹，如图13所示，从图中可以看出，随着废边宽度的增大，废边变形越小。

图13 废边轨迹与废边宽度的关系

在此过程中，废边的宽度增加了废边悬臂梁的刚性，而剪切力对于废边宽度无关，相同剪切力作用下，越宽的废边轨迹曲线越平缓。

通过拟合可以得到：当废边厚度为0.3 mm，圆盘剪切机运行速度为600 m/min时，不同宽度带钢废边的二次曲线。

30 mm宽废边对应二次曲线为

y=-0.221x2-0.055x-0.008=-0.221(x+0.125)2-0.00456

40 mm宽废边对应二次曲线为

y=-0.197x2-0.043x-0.007=-0.197(x+0.1)2-0.005

50 mm宽废边对应二次曲线为

y=-0.18x2-0.03x-0.007=-0.18(x+0.083)3-0.0058

不同宽度废边轨迹曲线与拟合的二次曲线如图14所示。

图14 不同宽度废边轨迹曲线与拟合的二次曲线

以废边轨迹的倾斜程度、顶点位置为参考，将不同宽度带钢的废边轨迹拟合成一条曲线为

y=-0.136b0.4(x+1.9b0.8)+0.001b0.44

(3)

式中，b为带钢宽度，mm。

(4)废边轨迹曲线。根据二次曲线的拟合，可以得到二次曲线各个系数分别与圆盘剪及废边各个参数的关系，于是，可以整合得到带钢废边轨迹与圆盘剪转速、废边厚度、废边宽度的关系表达式为

(4)

式(4)仅代表0～0.63 s内的带钢分析公式。随着时间推移废边长度增加，重量及速度会对上述关系产生决定性影响。分析方法及过程仍可按照相同流程进行。

5 结束语

切边圆盘剪是板带精整作业线上的核心设备之一，钢板剪切过程变形复杂,且变形程度大。溜槽的设计是影响剪切效果的重要因素之一，设计不当会造成带材触碰溜槽上壁，产生卡阻现象，影响剪切效果和机组的稳定生产。

废边带钢的运动轨迹是设计溜槽的重要依据,准确地获得废边的运动轨迹非常重要。因此,在对溜槽的设计过程中,通过有限元数值模拟，得到了剪切瞬间带钢废边运动轨迹，根据轨迹的最高点和轨迹与水平面的最小夹角等来准确设计溜槽。

根据圆盘剪的剪切特点,按照实际设备数据,建立准确剪切过程的有限元模型,并采用LS-DYNA进行数值模拟得到剪切瞬间废边的运动轨迹。通过对废边的运动轨迹数据的分析处理并结合实际情况提取出轨迹与圆盘剪运行速度、废边宽度、废边厚度的关系，为溜槽的设计提供参考，在实际工程中具有很大的应用价值。