轨道线路调整后考虑习惯影响的居民出行方式变化
2021-05-06朱佳欣贾顺平
朱佳欣, 贾顺平
(北京交通大学交通运输学院, 北京 100044)
在日趋成熟的轨道网络和城市交通出行环境下,为完善局部轨网,改善出行条件,在规划中对线路提出调整方案。随着线路调整,起迄点(origin and destination,OD)间轨道出行效益产生变动,居民出行方式发生相应的转移,影响既有出行结构。研究线路调整下的出行方式选择变化情况,对于城市交通管理者优化资源配置,提高城市交通运行效率具有较大的现实意义,也为今后轨道线路变动下出行行为的研究提供一定的理论依据。
既有研究中,学者们多集中于探讨出行经济费用变动[1-2]或新方式投入使用[3-4]对出行结构的影响等问题,针对既有线路调整情况下居民出行方式选择的研究较少。且这些研究多基于个体完全理性的假设,认为个体总是能完全辨别各方式的出行效益并依此决策,忽略了重复性出行经历对选择的干扰,导致对居民出行选择机理解释不足,与实际不符。
实验与实证研究表明,个体受习惯等主观因素的影响,对出行效益的感知是有限的,导致对理性行为的偏离,在出行方式选择中表现出一定的黏性及对行为改变的抵抗[5-7]。部分学者在出行离散模型中加入了对习惯影响及有限感知的考量。Gao等[8]在效用函数中设置哑元变量表示出行惯性对方式转移的影响,但未对习惯影响进行明确的量化。张新洁等[9]构建了基于无差异阈值的多方式有限理性分层模型。Cantillo等[10]也为出行属性分别设置阈值来反映个体对属性变化的有限感知,但均未考虑实际中个体的有限感知可能是动态变化的。
针对线路调整下的出行选择问题,在既有研究的基础上,考虑并量化个体出行习惯对其感知轨道交通效益变化程度的影响,构建包含阈值的动态效益变化感知函数,分析不同习惯影响程度下个体的出行方式变化情况。
1 问题背景
为缓解北京北部轨道交通线路供需压力,规划在西二旗与回龙观之间将既有13号线分为A、B两段,形成两条交叉的“X”形线路。既有13号线于2002年开通运营,北侧为居住密集区,西侧为大量的产业园区,当前线路西北段各站点进出站客流量大,满载率已超过120%。拆分后13A线由既有13号线西段继续向东北延伸至居住区并增设站点;13B线则由既有13号线东段继续向西延伸,可达产业园区,两线路通过新建站点进行换乘。拆分线路预计于2022年底开通,城市北部轨道交通出行条件发生变化,居民出行在轨道交通、公交车和小汽车三种方式间发生一定程度的转移,影响出行结构,且不同起讫点之间居民出行方式的变化情况有所不同。
2 线路调整下居民出行方式决策机理分析
由于个体在OD之间进行重复性较高的出行,易对某种方式产生偏好并重复选择,形成出行习惯,需要首先定义个体对习惯出行方式的偏好为习惯依赖性。
出行环境变化后,一方面,寻优心理使得人们尝试使用效益更优的方案;另一方面,受出行习惯影响,当使用另一种方式出行所付出的成本没有显著减少或期望提升的效益不明确时,人们往往会抑制行为的改变,保持习惯方式出行[11],此时个体为有限理性行为人。随着效益变化增大,这种抑制作用逐渐削弱,个体逐渐回到理性状态。因此随着线路调整,个体出行决策过程可分为两类讨论。
(1)OD之间采用轨道出行的效益降低。受换乘增加等因素的影响,OD间轨道出行效益下降。原轨道乘客向公交车、小汽车转移,但受轨道交通依赖性的抑制,转移率低于乘客在完全理性状态下达到的水平。原公交车、小汽车乘客保持既有出行方式不变。
(2)OD之间采用轨道出行的效益提高。线路调整后,OD间轨道出行可达性增强,避免了换乘接驳环节,出行效益提升。原公交车、小汽车乘客受到轨道交通的吸引,向轨道交通转移,转移率低于乘客在完全理性状态下达到的水平。原轨道乘客保持轨道出行不变。
综上所述,当轨道线路调整时,出行者方式决策不仅与各方式的客观效益相关,还会受到个体出行习惯的影响,且不同OD间的方式转移情况有所不同。
在进行出行方式选择模型建立前,首先做出如下假设。
假设1 既有接驳公交随线路变动发生相应调整,公交线网中其余线路及发车情况不发生变化。
假设2 道路路网结构不发生变化。
3 考虑习惯影响的出行选择模型构建
3.1 模型架构
考虑到交通方式间的相似性与差异性可能会导致出行转移的条件有所不同,同时为避免MNL(multinomial Logit)模型的无关选择独立性(independence of irrelevant alternative,IIA),将交通方式选择进行分层决策。根据三种交通方式的属性,将其分为私人交通和公共交通两类,其中私人交通指小汽车,公共交通包含公交车和轨道交通,NL方式选择模型分层如图1所示。
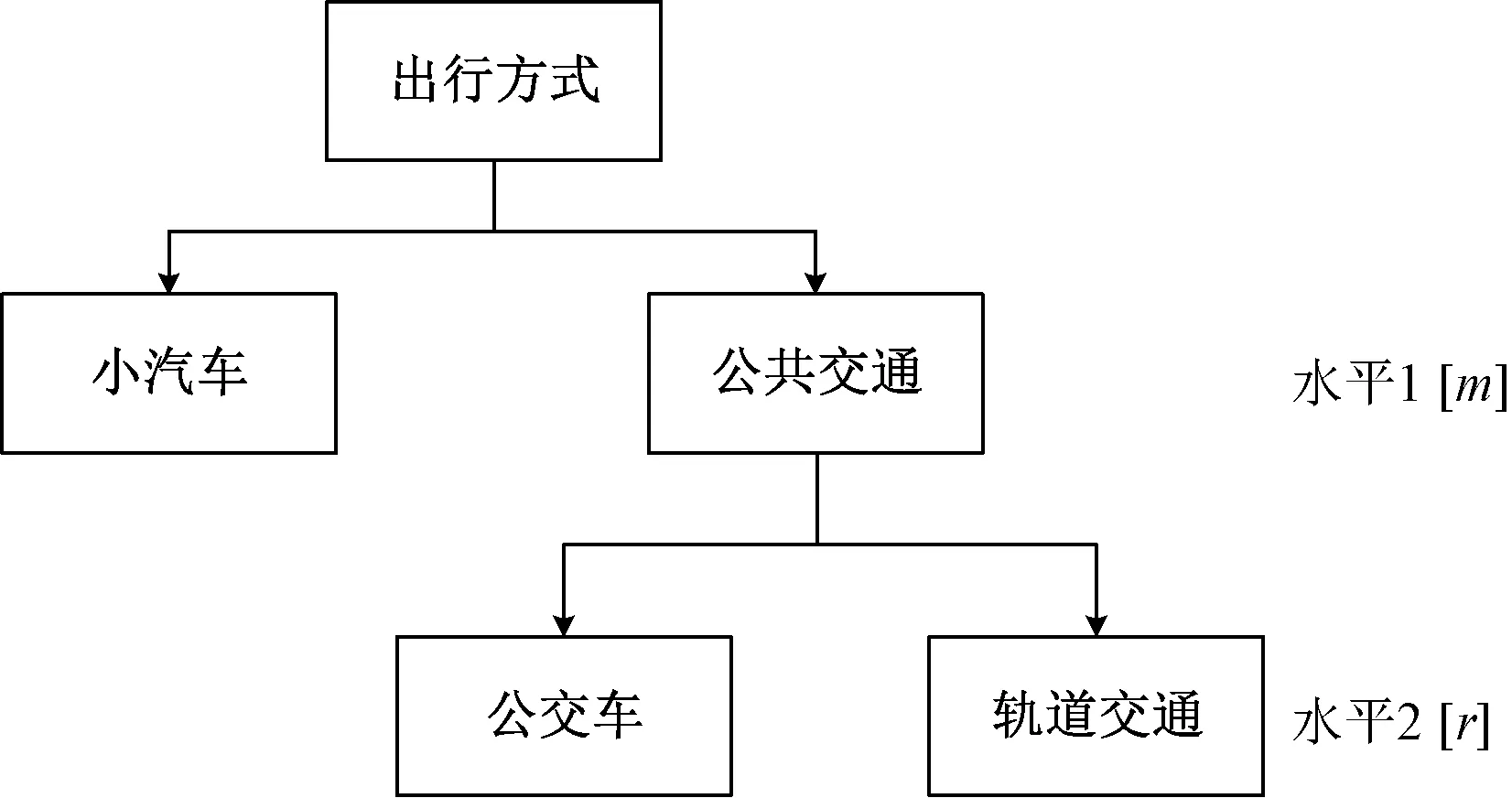
图1 出行方式选择模型结构Fig.1 Travel mode choice model structure
3.2 效用函数与选择概率
根据非集计模型中随机效用的表达形式,各方式的效益函数可表达为
Ui=Vi+εi
(1)
(2)
式中:Ui为选择方式i出行的效益;Vi为方式i的固定效益;εi为不可观测的随机项;xi,j为影响方式i固定效益的第j个属性变量;属性变量总数为n;θi,j为对应属性变量的权重;随机项εi相互独立且服从Gumbel分布。
轨道线路调整后,方式出行效益的变化值为ΔVi,ΔVi由线路调整后方式i的效益V′i与调整前的效益Vi之差表示为
ΔVi=V′i-Vi
(3)
上述模型结构中,ΔVrail=a,ΔVpub=b,公交车和小汽车出行效益不发生变化。
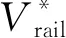
(4)
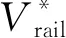
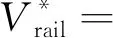
f(ΔVrail), |ΔVrail|>δ2
(5)
式(5)中:f(ΔVrail)为个体对轨道效益变化部分的感知值,f(ΔVrail)≤ΔVrail。
(6)
(7)
式中:δ1为水平1下的阈值;λ2为水平2下效用函数的系数。
综合式(3)~式(7),轨道线路调整后,各方式的感知效益可表示为
(8)
根据图2所示分层结构及条件概率,线路调整后各方式选择概率为
(9)
(10)
p(r)=p(r|m)p(m)
(11)
式中:p(m)、p(r)分别为水平1、2下各方式的选择概率;p(r|m)为在选择了方案m的条件下选择方式r的条件概率;λ1、λ2为待估参数。
3.3 效益变化感知函数模型
为了对f(ΔV)进行定量描述,考虑了影响个体感知效益变化的两个因素。
一是个体在进行方式决策时,对习惯出行方式的依赖程度会影响效益变化的感知值。以Ri表示个体对方式i的依赖性,Ri∈[0,1]。
Ri越大,方式依赖性抑制个体行为改变的作用越大,当出行环境变动,个体决策所受干扰越大,对出行属性的变化越不敏感,f(ΔV)越偏离ΔV;反之,Ri越小,个体的习惯选择倾向越不明显,对出行效益变化越敏感,f(ΔV)越接近ΔV。
二是个体在进行方式决策时,效益变化值与阈值的相对比值大小会影响效益变化感知值。定义该比值为有效变化比率,以γ表示,则有
(12)
γ越大,效益变化值中对个体感知产生作用的部分所占比重越高,个体面对出行环境变动时越客观,对出行属性变化的感知就越清晰,f(ΔV)越接近ΔV;反之,γ越小,个体对出行属性变化的感知越模糊,f(ΔV)越偏离ΔV。
综上所述,f(ΔV)不仅与ΔV有关,还受到R和γ的共同影响。定义一个效益变化感知因子Φ,有f(ΔV)=ΔVΦ,Φ=Φ(R,γ),Φ∈(0,1]。
R、γ分别与Φ呈负、正相关,且满足以下关系:
(1)当R=0时,个体在历史时段T内平均的选择各种方式出行,不存在习惯依赖性,对效益变化值的感知为实际值,即Φ=1,f(ΔV)=ΔV。
(2)当R∈(0,1]时,个体对习惯出行方式存在不同程度的依赖。在一定的依赖程度R下,f(ΔV)的值取决于γ,并且有①当γ趋近于0时,效益变化相对阈值为0,则个体对该变化基本无感知,假设此时Φ(γ)=c,c为常数;②当γ逐渐增大,个体对变化值的感知越真实,Φ(γ)逐渐趋近于1;③随着效益变化值相对阈值增大,个体面对效益变化时的客观程度也逐渐增大,因此Φ(γ)随γ变化的增速也随着γ的增大而增加。
因此假设Φ(γ)服从式(13)和图2分布,Φ服从式(14)。
Φ(γ)=exp[α(γ-1)+d]
(13)
Φ=Φ(R,γ)=Φ(γ)R
(14)
式中:α、d为常数。
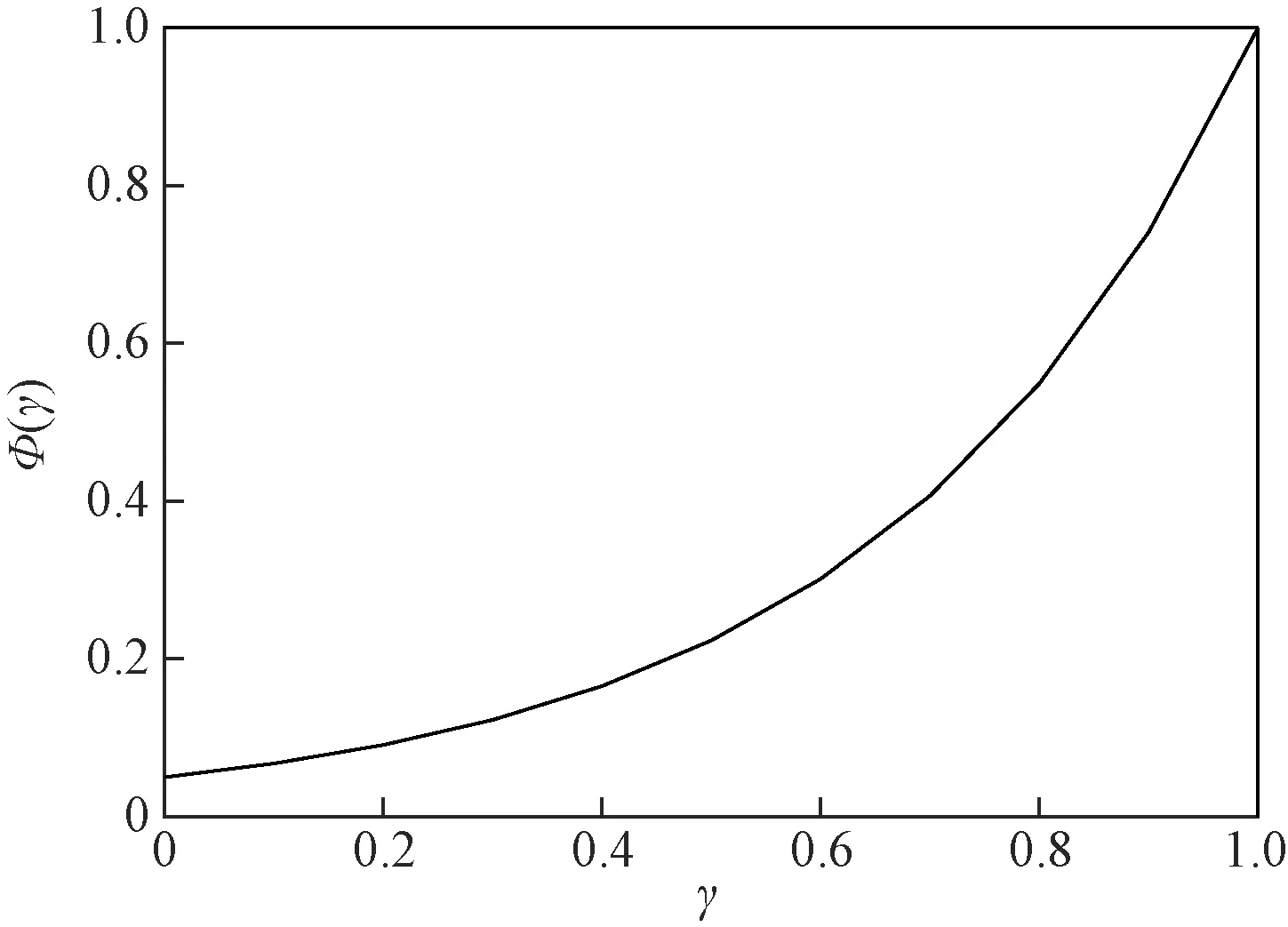
图2 Φ(γ)拟合图Fig.2 The matching graph of Φ(γ)
4 案例分析
4.1 案例描述
选取既有13号线沿线一个典型居住小区为O,工作区为D。该OD间既有出行网络可抽象成图3,线路拆分后,研究区域内轨道出行线路如图4所示,R1、R2、R4为轨道进出站点,R3为换乘站点。OD间轨道出行可达性与便捷性发生变化,个体出行在三种方式间发生转移,考虑拆分带来的差异性影响,在原D区域内确定两不同终点D1、D2分别分析。
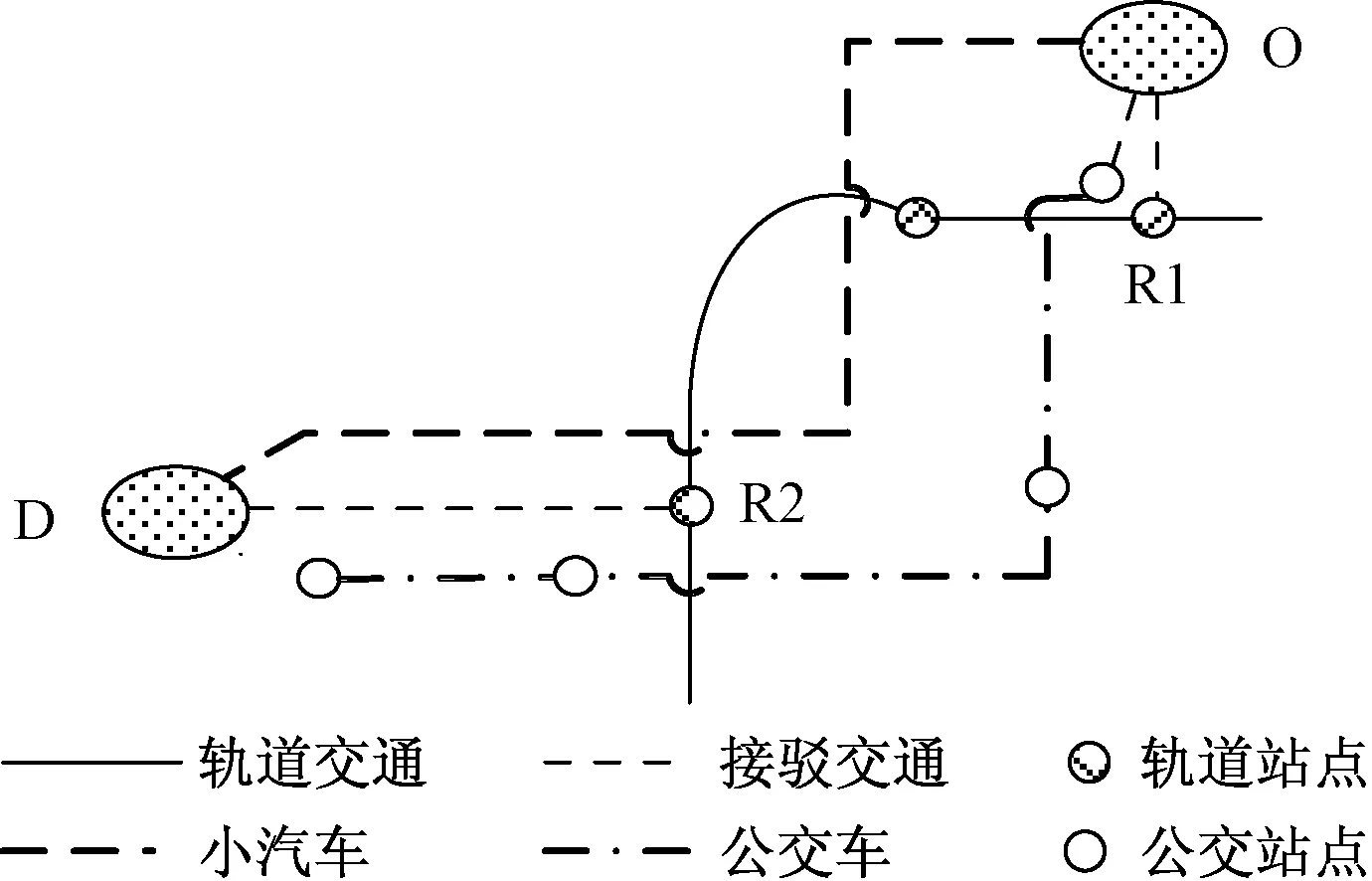
图3 既有出行网络示意图Fig.3 Existing travel network
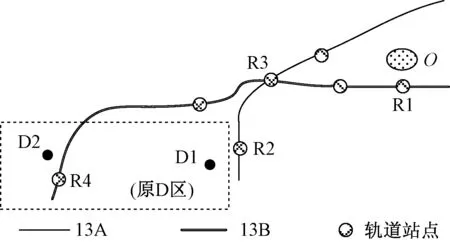
图4 调整后轨道出行线路图Fig.4 Route of urban rail after the adjustment
以时间t、费用e为效用函数变量,其中时间包括各方式出行时间、接驳时间和步行时间。根据实地调查和资料搜集,拆分前后轨道出行信息对比如表1所示,各变量对应权重及模型中的参数取值[1]如表2所示。

表1 拆分前后轨道出行情况对比
注:+、-、—分别表示拆分后对应属性值增加、减少、不变化。

表2 模型参数取值Table 2 Parameter values in the model
注:θbus,t、θrail,t、θwalk,t、θcar,t分别为公交车、轨道交通、步行和小汽车出行的时间属性权重,θbus,e、θrail,e、θwalk,e、θcar,e分别为公交车、轨道交通、步行和小汽车的费用属性权重,λ1、λ2分别为水平1、水平2下效用函数的系数。表4同。
4.2 结果分析
4.2.1 案例结果
通过模型求解得到两组OD在线路调整后的方式选择结果如表3所示。
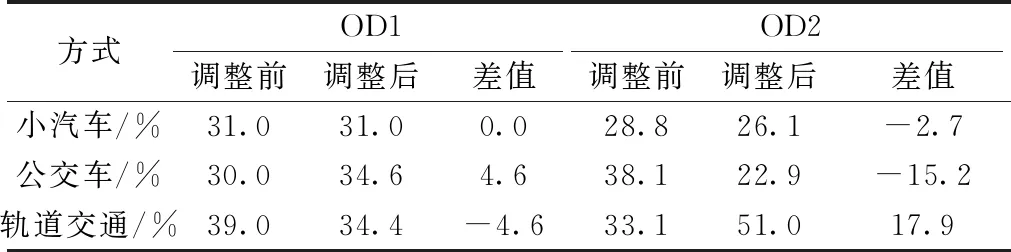
表3 出行选择结果比较
在线路调整后,OD2轨道效益的变化率约为OD1的两倍,因此OD2的出行结构变动幅度相对OD1更大,且影响的方式更多。
OD1:选择轨道交通的概率为34.4%,与调整前相比下降4.6%,说明轨道出行效益下降后,部分轨道客流会向其他方式转移。相应的,公交车选择概率上升了4.6%,小汽车选择概率则未上升,这是由于在本案例中OD1间公共交通效益的变化值小于水平1下方式转移的判断依据δ1,因此个体对该变化无反馈,小汽车的选择概率与调整前一致。
OD2:与调整前各方式的选择概率相比,小汽车、公交的选择概率分别下降了2.7%、15.2%,可见轨道出行效益的提升将吸引小汽车和公交车乘客向轨道交通转移,且公交乘客发生转移的概率更大。这一点与现实较为相符,小汽车作为私人交通,在舒适性、可达性等方面具有优势,而轨道交通与公交同属公共交通范畴,两者在出行属性上具有较高的相似性,因此轨道效益的提升对于公交乘客来说更具有吸引力。
4.2.2 灵敏度分析
以OD2为例,分析方式选择随模型参数变化的情况。
δ1对线路调整前后各方式选择概率变化程度的影响如图5所示。随δ1增大,小汽车选择概率变化值|Δpcar|先逐渐减小,后保持为0,说明δ1越大,个体保持小汽车出行的概率越大,而当δ1增大至一定值时,公共交通出行效益的提升已无法吸引小汽车乘客向其转移,此时向轨道交通转移的客流均来自公交车。当|Δpcar|随δ1增大而减小时,小汽车选择概率增大,公共交通选择概率相应减小,因此在轨道效益提升的吸引下,公交车选择概率降低程度|Δpbus|随δ1的变化表现为先增大后保持不变(16%),轨道交通选择概率提高程度|Δprail|随δ1的变化表现为先减小后保持不变(16%)。
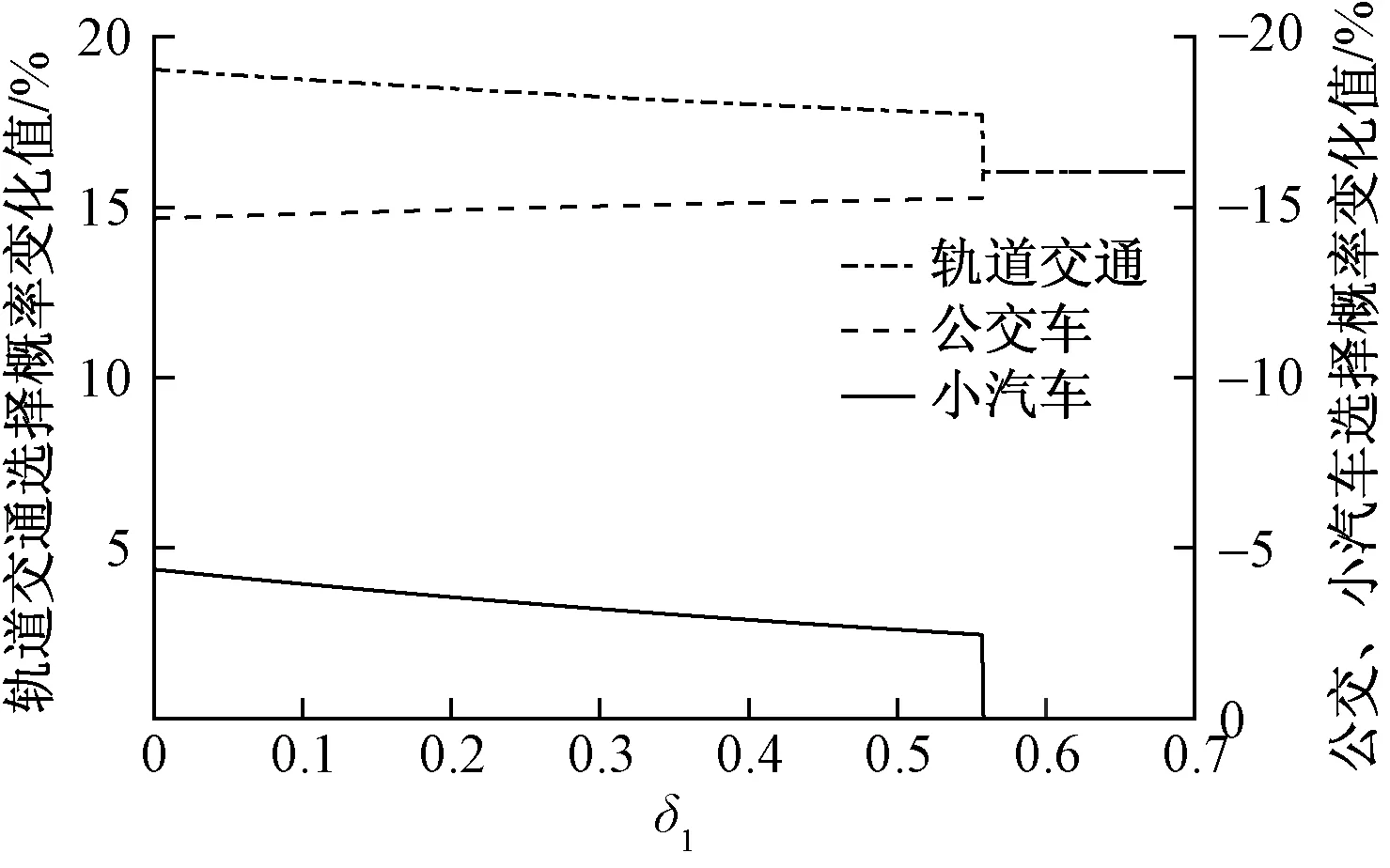
图5 δ1对选择概率变化值的影响Fig.5 Influence of δ1on the variation of choice probability
δ2对各方式选择概率变化程度的影响如图6所示。|Δpcar|不受δ2变化的影响,客流由小汽车向公共交通转移的概率始终为定值(2.7%)。随着δ2增大,个体由公交向轨道交通转移条件越高,对轨道交通效益提升的感知越模糊,公交乘客保持既有方式出行的概率越大,|Δpbus|逐渐减小。相应的,轨道交通选择概率提升程度|Δprail|也逐渐减小,且两者随δ2减小的速度相同。
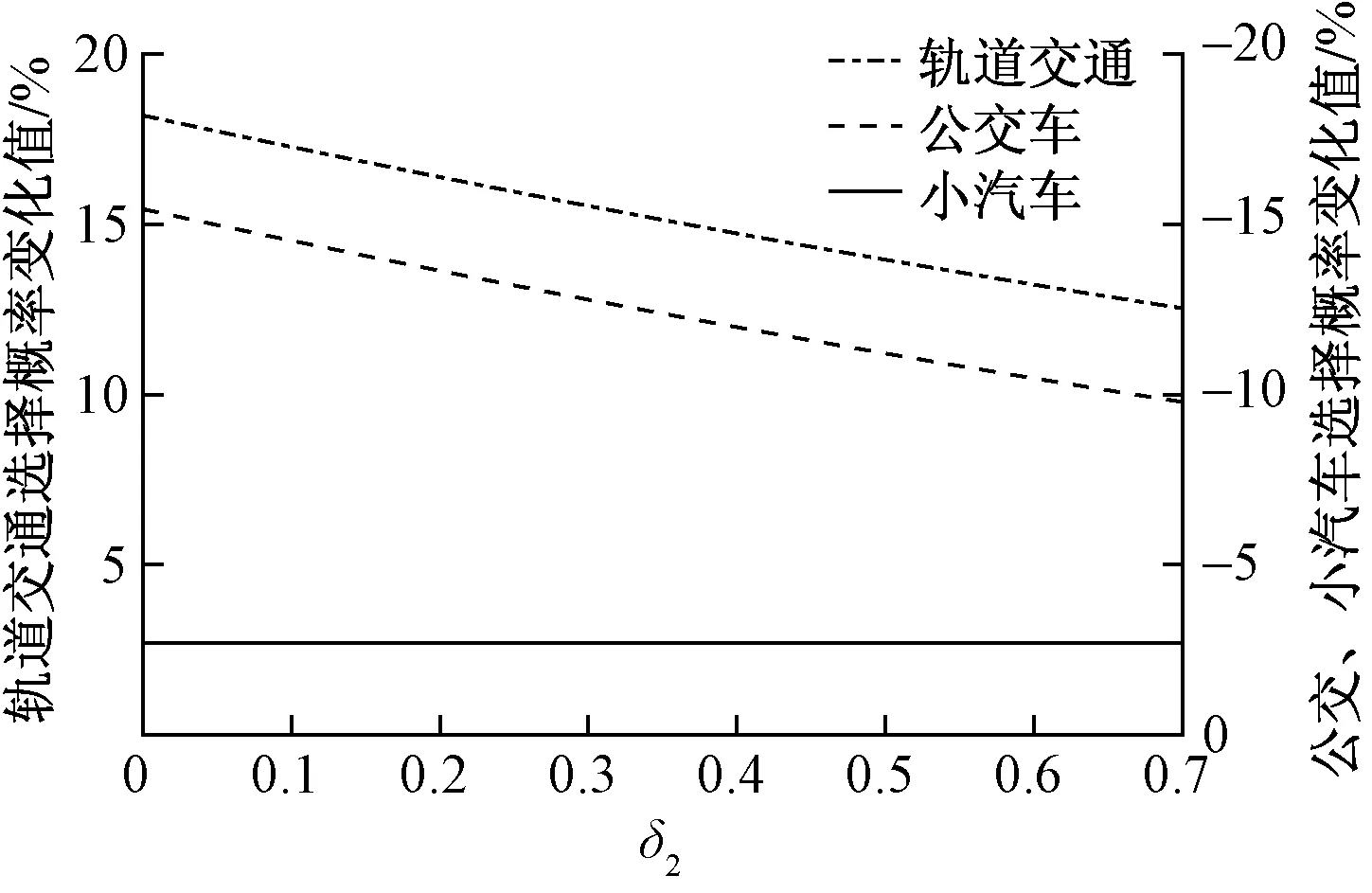
图6 δ2对选择概率变化值的影响Fig.6 Influence of δ2on the variation of choice probability
由表3可知,公交车客流是向轨道交通转移的主要对象,因此公交车出行依赖程度对轨道线路调整的效果有重要影响。Rbus对轨道交通选择概率变化程度的影响如图7所示。当δ1=0、δ2=0时,即模型是不考虑习惯影响的传统NL模型,公交车向轨道交通转移不受Rbus大小的影响,|Δprail|为定值(19.3%)。当δ1≠0,δ2≠0时,|Δprail|随Rbus的增大逐渐减小,说明在考虑习惯影响时,个体对公交车出行依赖性越大,越难以向效益提升的轨道交通转移。随着阈值的增大,Rbus对|Δprail|的影响也越大。
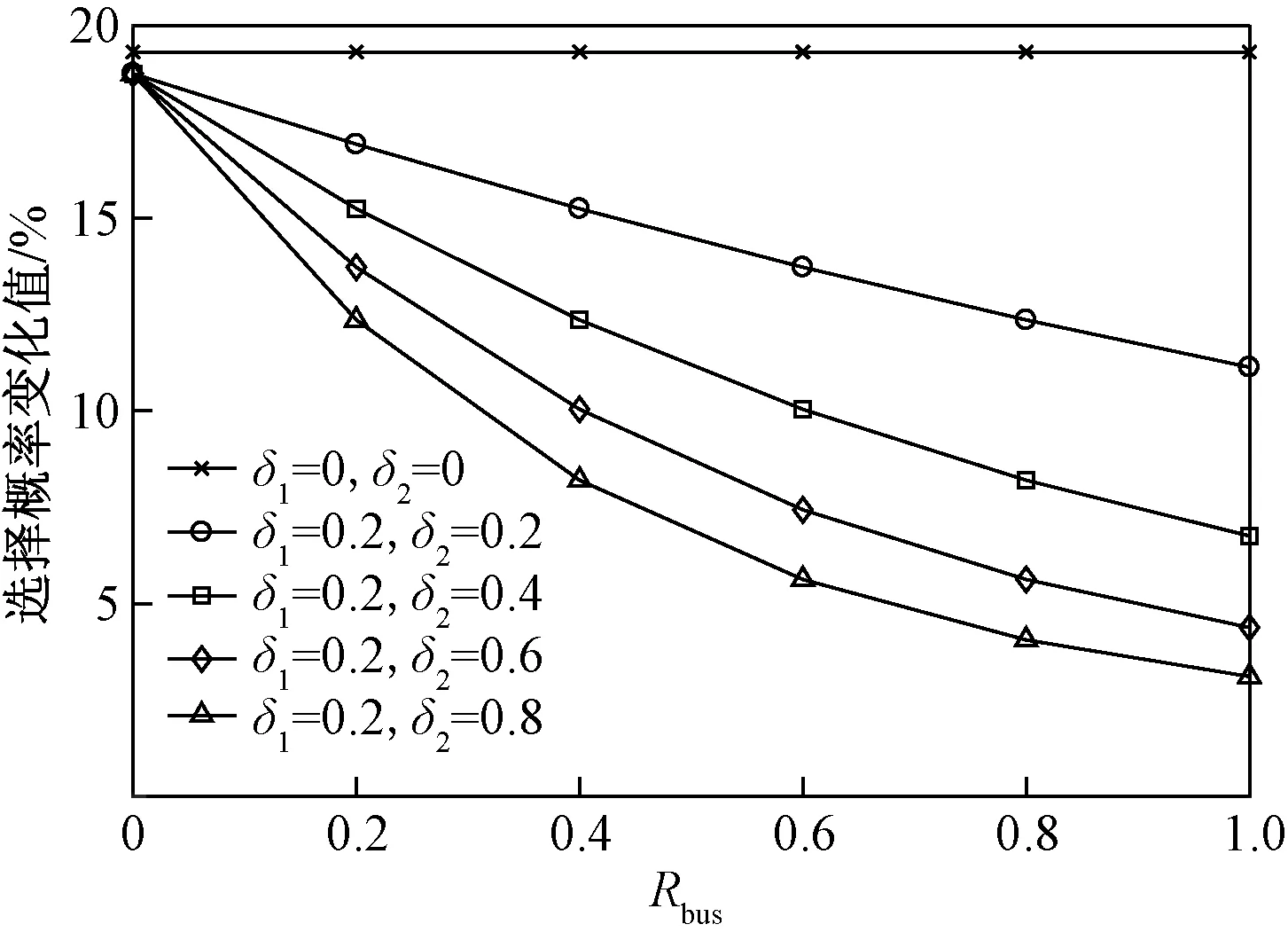
图7 Rbus对轨道交通选择概率变化值的影响Fig.7 Influence of Rbuson the variation of choice probability of urban railway
4.3 出行优化政策
从案例结果可以看出,13号线拆分对各 OD间轨道交通出行产生的影响有所不同,且在个体出行习惯的影响下,拆分效果难以达到预期。因此,轨道交通线路的调整还应配合城市公共交通体系的不断改善,提高服务水平与质量,才能达到线路调整的理想效果。具体提出以下改善政策。
(1)对于OD间轨道出行在13号线拆分后受到不利影响的情况,主要原因在于换乘环节的增加,因此两线换乘站的设计可考虑同站台换乘,缩小主要客流的换乘时间。
(2)13号线拆分对小汽车乘客的吸引较小,客流转移大部分发生于公共交通系统内部。可在地铁站点和住宅区周边规范化增设共享单车投放点,提升轨道交通出行“最后一公里”便捷性,进一步扩大出行优势,提升线路拆分影响力。
(3)对公共交通间换乘给予一定的折扣优惠,减少公共交通出行费用。
配套政策下各方式选择概率变化情况如表4所示。在线路调整的基础上,小汽车出行选择概率分别又下降了1.2%和1.8%,轨道交通的选择概率则进一步上升,公共交通整体出行比例提高。说明完善配套策略,将有助于减小习惯对决策的影响,实现线路调整的预期目标。

表4 选择概率变化Table 4 Change of choice probability
5 结论
针对轨道线路调整下居民的出行选择行为,本文放松了既有研究中个体理性认识各方式出行效益的假设,考虑习惯对行为变化的抑制,改进了效益函数的计算,构建了包含效益变化感知函数的NL模型,最后以13号线拆分为例验证了模型的可行性和有效性,并总结得出如下结论。
(1)轨道线路调整并不总是会提升轨道出行效益,对不同的OD可能会带来相反的影响。但在两种情况下,线路调整皆对轨道自身选择概率的影响最大,公交车其次,小汽车受影响程度最小。且轨道效益变化率越高,影响越明显。
(2)阈值越大,个体保持习惯方式出行的概率越大,且模型上层阈值会对下层的决策产生影响,下层阈值则对上层选择无影响。
(3)方式依赖程度越大,决策时受习惯抑制作用越大,越难以向实际效益更优的方式转移。且阈值越大,方式依赖性对决策结果的影响越明显。
(4)轨道交通线路调整配合与之适应的换乘接驳措施和优惠的出行服务政策,有助于提升轨道出行优势,削弱习惯抑制行为改变的影响,提高居民绿色出行比例。
