综合管廊排水系统潜水泵的临界淹没深度

刘 阳, 兰惠清*, 张峥茂, 岳 彬, 高荣琴

(1.北京交通大学机械与电子控制工程学院， 北京 100044； 2.北京航空工程技术研究中心， 北京 100076)

综合管廊是指在城市道路、厂区等地下建造的一个隧道空间[1]，将电力、通信、燃气、给水、热力、排水等市政公用管线集中敷设在同一个构建物内，并通过设置专门的投料口、通风口、检修口和检测系统保证其正常运营，实施市政公用管线的“统一规划、统一建设、统一管理”[2]的建筑设施。随着城市的飞速发展，以传统直埋方式敷设的地下管线已经不能很好地满足现代化城市的发展需求，综合管廊的建设成为城市发展的必然趋势[3]。由于综合管廊内设有雨水渗透、外部通风口、人员进出口、投料口等外部开口，一旦发生紧急进水，排水系统保障综合管廊安全运行的重要附属设施。

王俊岭等[4]对智慧城市排水管道试验模型重力流、压力流不同工况进行了堵塞试验及堵塞影响因素研究。刘羽[5]以中国现有的综合管廊排水系统为前提，结合中国标准中提到的排水管线入廊基本原则，通过入廊条件、断面形式、技术要点三个方面，对城市道路综合管廊排水管线入廊相关技术进行了研究。谢伟[6]通过对综合管廊结构及内部设施的分析导致管廊内积水的原因，讨论了综合管廊排水设计要点及措施。Johnson等[7]针对可持续城市排水系统对德国柏林某社区的排水系统的效益和经济价值进行了评估，并将其与文献中发现的典型成本评估进行了比较。Ngo等[8]提出一种新的基于多场景的两阶段设计方法来优化城市污水系统的布局和水力设计(确定管道尺寸和孔深度)。综合中外文献，专门针对综合管廊排水系统方面的研究文献较少，但对于管道排水、水力工况分析、抽吸试验以及经济效益均开展了很多研究，采用方法主要有试验法、比较法、理论计算法等。而实际上，中国与国外的排水系统在具体的研究数据方法有很大不同，基础理论尚未完善、影响因素较多、动态过程模拟缺失是目前存在于管廊排水系统潜水泵临界淹没深度的三个重要问题，因此，针对管廊排水系统中潜水泵的临界淹没深度进行深入研究具有重要意义。

管廊排水系统主要包括排水渠、集水坑、潜水泵、液位传感器、止回阀、截止阀、压力表、压力传感器等。管廊集水坑内最重要的设备为潜水泵，潜水泵的运行安全将直接影响管廊排水系统的排水能力。廊内发生排水事故时，集水坑内的水位迅速上涨，当达到警戒水位时，潜水泵迅速开启，此时潜水泵进水口处的流场区域比较复杂，并将源源不断地产生进气漩涡，进气漩涡经由潜水泵泵体排出至排水管内。进气涡进入潜水泵内将会形成气囊而引发流蚀损坏、振动、噪声及泵效率下降等现象[9]。

工程表明，适宜的吸水口安装位置将有效抑制涡的形成,延迟连续吸气涡的到来并降低水泵中气囊形成的风险，这对水泵的稳定工作和降低工程成本起着至关重要的作用[10]。自20世纪70年代起，各国学者通过水力模型试验对吸水口进水流态进行了研究。其中，基于弗劳德数和淹没深度等无量纲参数的研究取得了较好的成果。继Gordon[11]基于水电站研究引入无量纲数对临界淹没深度的关系后，中外有学者提出了一些无量纲数的经验公式。Farell等[12]对于漩涡早期的研究表明，漩涡的产生、发展受取水口淹没水深、取水量、取水口边界、重力、黏滞力、表面张力及上游来流水力条件等多种因素影响。

在一种对综合管廊排水系统的发明专利[13]基础上，现运用计算流体动力学软件对管廊的排水系统进行数值模拟分析，对集水坑内潜水泵达到警戒位时竖向排水的情况进行讨论[14-15]，并在前人研究的基础上，建立管廊排水系统潜水泵相对淹没深度与无量纲数之间的经验公式，为管廊排水系统的设计及安全评价提供参考。

1 研究对象和无量纲参数的选择

通过对北京市昌平区、上海市松江区及海口市等多地考察，确定了中国典型的综合管廊排水系统横截面示意图，如图1所示。

图1 典型管廊排水系统示意图Fig.1 Schematic diagram of a typical utility tunnel drainage system

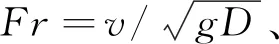
Knauss[17]针对不同进口方向，提出了在无破漩装置时表征相对淹没深度与弗劳德数关系的经验公式为

s/D=2Fr+0.5

(1)

Hecker[18]通过对水泵进水口模型试验的研究，总结出取水口临界淹没深度与管道弗劳德数满足的关系式为

s/D=2.3Fr+1

(2)

式(2)被美国列为水泵设计标准的推荐公式。

何耘等[19]建立通过水力试验视“出现较强间断吸气涡且即将发生连续吸气涡的淹没深度”为水泵吸水口临界淹没深度，拟合经验公式为

s/D=0.76Fr+0.47

(3)

在管廊排水系统运作时，雷诺数和韦伯数都在一个足够高的数值区间内波动，水的黏性力和表面张力对涡旋的影响相对于相对淹没深度和弗劳德数影响较小，故可以忽略。因此，以弗劳德数为主要影响因素研究相对淹没深度与其之间的关系。

2 基本参数计算

2.1 暴雨强度公式与水流速度

研究对象位于上海松江区地下综合管廊，上海市地方标准《暴雨强度公式与设计雨型标准》(DB31/T 1043—2017)中，降雨强度计算公式为

(4)

式(4)中：q为设计降雨强度，L/(s·hm2)；P为设计重现期，年；t为降雨历时，min。

某特定暴雨强度的重现期指大于或等于该值的暴雨强度可能出现一次的平均间隔时间，重现期与频率成反比[20]。设计重现期可根据中国《建筑给水排水手册》[21]来选取。降雨历时t可根据不同地理环境下时空条件来确定。计算设计降雨强度q，然后转化为综合管廊内排水系统的水流速度。

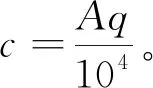
统一为国际单位，得

(5)

式(5)中：A为单元廊舱的占地面积，m2；c为在此面积上单位时间降雨量，L/s；Q为流量，m3/s。

设管廊排水渠截面半径为r(m)，则

(6)

将式(5)代入式(6)，得任意管廊模型内排水系统的输入水流速度公式为

(7)

管廊内排水系统的输入水流速度(m/s)为

(8)

2.2 累积雨量过程线与变流量工况下的输入水流速度

2.2.1 累积雨量过程线

累积雨量过程线是表征当地降雨过程的重要曲线，是降雨强度公式的积分[22]。令累积雨量为S(mm)，则

(9)

对式(4)积分，得

(10)

得

F(t)=5 734.52(t+7)0.444+C

(11)

式中：F(t)为单位为L/hm2时的累积雨量函数，S(t)为得到单位为mm的累积雨量函数，需在F(t)基础上乘以系数C1进行转化，即

S(t)=C1F(t)

(12)

其中，

(13)

即

S(t)=0.573(t+7)0.444+10-4C

(14)

为确定常数C，需查询《暴雨强度公式与设计雨型标准》(DB31/T 1043—2017)[23]中的“重现期P=5年120 min设计雨型表”来确定初始条件。选取t=5 min时降雨强度为1.255 mm/min，故S(5)=6.275 mm，代入方程得C=4.467×104，故累积雨量函数S(t)为

S(t)=0.573(t+7)0.444+4.467

(15)

利用式(15)可得到任意降雨历时下综合管廊的累积雨量，可为后续的分析奠定基础。

2.2.2 变流量工况下的输入水流速度

单元廊舱长度为200 m，宽3.5 m，模型截面直径为50 mm，代入式(8)，得速度v(m/s)与时间t(min)之间的函数关系式为

(16)

2.2.3 累积雨量过程线与输入水流速度的对比分析

累积雨量过程线与输入水流速度的函数曲线对比如图2所示。

图2 累积雨量过程线与输入水流速度的函数曲线Fig.2 Cumulative rainfall process line and input water flow velocity function curve

随着降雨历时的增加，累积雨量逐渐增多，输入水流速度逐渐减少。这是由于在降雨开始时，累积雨量过程线的斜率较大，降雨强度较高，致使单位时间内流入廊舱内的水量急剧增加，水流速度较为迅速；随后，累积雨量过程线的斜率逐渐变小，降雨强度逐渐变弱，单位时间内流入舱内的水量减小且趋于平稳，水流速度较小。

3 管廊排水系统的仿真

3.1 数学模型简化与计算

采用多相流模型(volume of fluent model，VOF)和标准的k-ε模型来研究空气与水的气液两相流模拟。忽略集水坑内空气与水的气液两相流流动受温度的影响，故计算使用以下三个方程组，分别为质量守恒方程组、动量守恒方程组和标准的k-ε模型的湍动能k和湍流耗散的输运方程组。

(1)水为不可压缩流体，质量守恒方程组可简化为

(17)

式(17)中:ρ为密度；i、j、k为正交单位向量；∇为矢量微分算子；ux、uy、uz为单位方向向量上的速度。即

∇·u=divu=0

(18)

(2)动量守恒方程组为

(19)

式(19)中:f为体积力；τ为黏性力；p为压力。

(3)标准的k-ε模型的湍动能k和湍流耗散的输运方程组为

(20)

式(20)中：Gk为层流速度梯度湍动能项；Gb为浮力湍动能项；YM为可压缩流动中湍流脉动膨胀到全局过程中对耗散率的贡献项；C为常数项；σk、σε为湍流Prandtl数；Sk、Sε为自定义湍动能项和耗散源项。

3.2 建模

对排水管道公称直径为100 mm的集水坑进行三维建模，如图3、图4所示。为确保后处理关于涡的准确性，采用全局非结构化网格方案[24]；为保证模型的建造及模型试验结果的准确性，原型与模型长度采用2∶1的缩比。

a、b、c分别为集水坑的长、宽、高，m；d1、d2为排水沟直径；d3为排水管直径图3 廊舱排水系统模型Fig.3 Utility cabin drainage system model

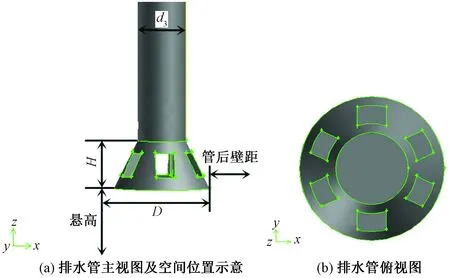
D为喇叭口外径，mm；H为喇叭口高度，m图4 排水管示意图Fig.4 Schematic diagram of the drain pipe

3.3 求解边界和初始条件

管廊排水过程是一种非稳态过程，采用压力基求解器；流入的水流与集水坑内的水混合处及排水管沿程均为湍流，采用标准k-ε模型；多相流模型为两相，空气为主相，水为第二相。由于在集水坑内混合的水流是一种具有自由液面的水流，水流的表面压强为大气压强，即相对压力为0，故采用明渠流动，隐式计算[25]；边界条件为速度进口和速度出口。

工作压力为大气压，两速度入口处流场速度根据不同工况设置。排水管道的出口处设置为速度出口，本文模拟的是集水坑内的抽水过程，故速度出口处的流场速度应为负值，水的体积分数为100%；在进行初始化后，对集水坑内的水位进行标定。管廊集水坑内一般设有浮球开关水位控制器，当水位达到警戒位时，控制器控制潜水泵开启，排水系统开始运行。设集水坑内的初始液位为0.7 m。

4 结果分析与讨论

4.1 涡的形成

图5为z=0.4、0.5、0.6 m截面的速度矢量图。

图5 不同z截面的速度矢量图Fig.5 Speed vector of different z-section

一方面，当潜水泵开始工作时，水泵叶轮高速旋转，吸水口处形成真空，在大气压的作用下集水坑内的水大量涌入附有侧面开口的喇叭口；另一方面，两进水口源源不断地输入水坑，汇集有复杂速度的水湍流与集水坑的原有水面相接触，足量的空气混入水内，在集水坑原有的水内形成大量气泡。水泵吸气造成的吸力在水内不同深度形成不同的速度梯度，与涌入携带有气泡的水流相作用，在管壁、集水坑壁、喇叭口肋板的挤压下，水流速度矢量剧烈变化，在不同深度的截面上可观测到不同程度的涡。

4.2 临界淹没深度的讨论

集水坑内专用的潜水泵与一般消防水泵、水库吸水系统的水泵不同，其结构上采用喇叭口的形式，并在其侧面开口。采用这样的结构一方面可以增加吸水源的个数，从而一定程度上提高排水系统的吸水能力；另一方面可以在水流流场中阻碍吸气涡流线的分布从而对涡的形成产生一定的干预作用。同时，带有开口的喇叭口结构形式与普通的吸水管经验公式不同，若采用一般的吸水管经验公式来设计计算或评价集水坑内潜水泵的运行情况时，会产生一定偏差，影响工程上水泵的运行与维护。

为了方便讨论弗劳德数与临界淹没深度之间的关系，规定吸气涡到达附有侧面开口的喇叭口下沿端面时，下沿端面至集水坑内的最高水位高度为临界淹没深度。在工程实际中，流入集水坑内的水流量时而恒定，时而连续变化，故讨论临界淹没深度可分为三种情形。

4.2.1 理想条件下出口速度不同对临界淹没深度的影响

理想条件是指廊舱排水渠内无水流动(入口速度为0)，集水坑内日常积累积水水量达到警戒线导致水泵开启时的工况出口速度vex的设置如表1所示。

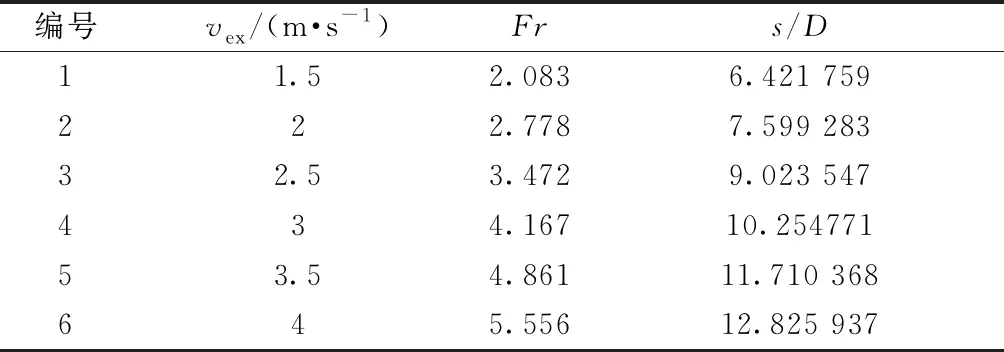
表1 理想条件下工况设定与后处理结果

从表1可以看出，临界淹没深度的幅值较大，说明集水坑积水在无外界条件影响下，涡自吸水口处向水面蔓延的梯度更大，此种工况在基本没有水面波动条件下传播范围更广。由统计表拟合得到临界淹没深度与弗劳德数之间的关系式为

s/D=1.87Fr+2.39

(21)

本模型结果与Hecker公式较为接近，计算流体动力学与试验结果的一致性说明了无外界扰动的潜水泵吸水过程更贴近于工程实际；拟合结果的斜率与Knauss公式更为相近，说明无破漩装置应用与集水坑内周边布置所形成的影响系数基本相同；与文献[19]公式相比，拟合结果不同的原因主要是本模型采取的吸水口为侧面带有开口的喇叭口，而文献[19]采用的是直立单管来进行试验。

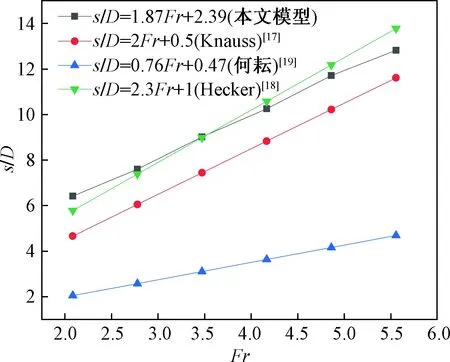
图6 理想条件下临界淹没深度与弗劳德数关系Fig.6 The relationship between critical submerged depth and Froude number under the ideal condition

4.2.2 入口速度恒定时出口速度不同对临界淹没深度的影响

根据降雨历时和设计重现期来确定两入口速度均为1.8 m/s，出口速度的设置如表2所示。在出口速度增大的同时，弗劳德数与临界淹没深度相应增大。在吸水口附近，每个吸水源的水体产生了较大的动量，这些较大的动量维持并延续了涡的存在。在计算流体动力学的非稳态迭代过程中，水位先有所下降，而后又逐渐上升，这是因为在汇集的雨水水流下降这个过程中，潜水泵会运行先抽掉一部分水，水位下降，当补充的水量与抽取的水量相一致时，水位达到瞬间的平衡状态；随着水流不断涌入，新进的雨水水量逐渐超过抽水水量，水位上升。

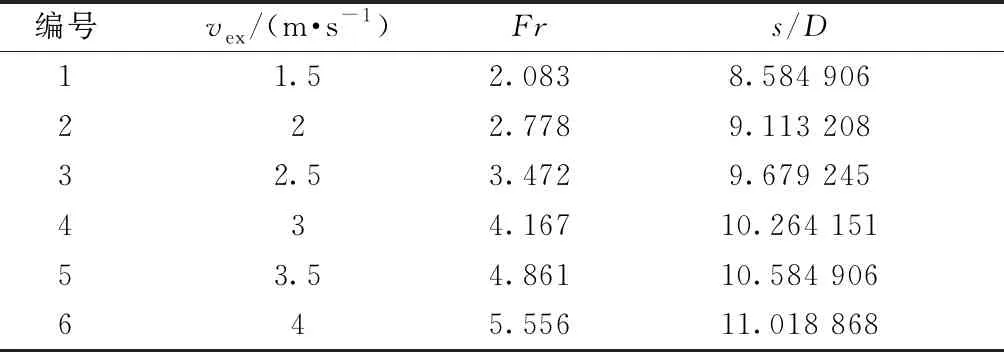
表2 入水速度固定条件下工况设定与后处理结果

涡在整个过程中在每个横断面上持续存在，由表2拟合得临界淹没深度与弗劳德数之间的关系式为

s/D=0.71Fr+7.18

(22)

将得到的拟合结果与以往学者的结果进行对比分析，结果如图7所示。本文模型结论与Hecker经验公式较为接近，这是主要是由于Hecker经验公式的进水口方向为水平，考虑到模型试验的弗劳德数均比较大的工况，试验条件设定与本试验较为吻合；本文模型拟合得到的斜率与文献[19]的经验公式较为接近，说明计算流体动力学得到的结论与试验结果之间较为一致，在常数项上的区别主要是由于本模型管道为集水坑用镀锌管道，公称直径较小，相对淹没深度较大；与Knauss经验公式相比，其相似性仅次于Hecker经验公式，尤其体现在斜率上，这是因为Knauss经验公式应用范围较广，并将多种进水口的布置方式考虑在内，故其斜率较大。

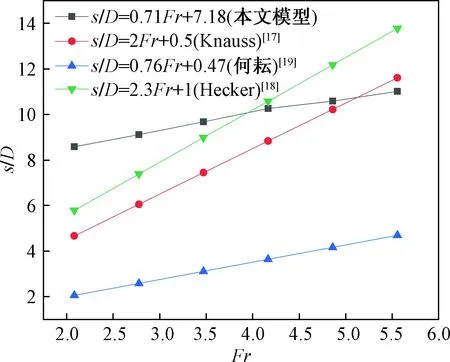
图7 入口速度固定条件下临界淹没深度与弗劳德数关系Fig.7 The relationship between critical submergence depth and Froude number under the water inlet velocity being fixed

4.2.3 入口速度连续变化时出口速度不同对临界淹没深度的影响

在工程实际中，综合管廊内汇集到集水坑内的水流流速不是一成不变的，而是时刻在发生变化。以异常降水为前提，计算出上海市松江地区累计雨量过程线并将其推导至单元廊舱背景下廊内引水渠内水流流速。同样地，统计在各种工况下，入口速度ven、出口速度、弗劳德数与临界淹没深度的数据，如表3所示。

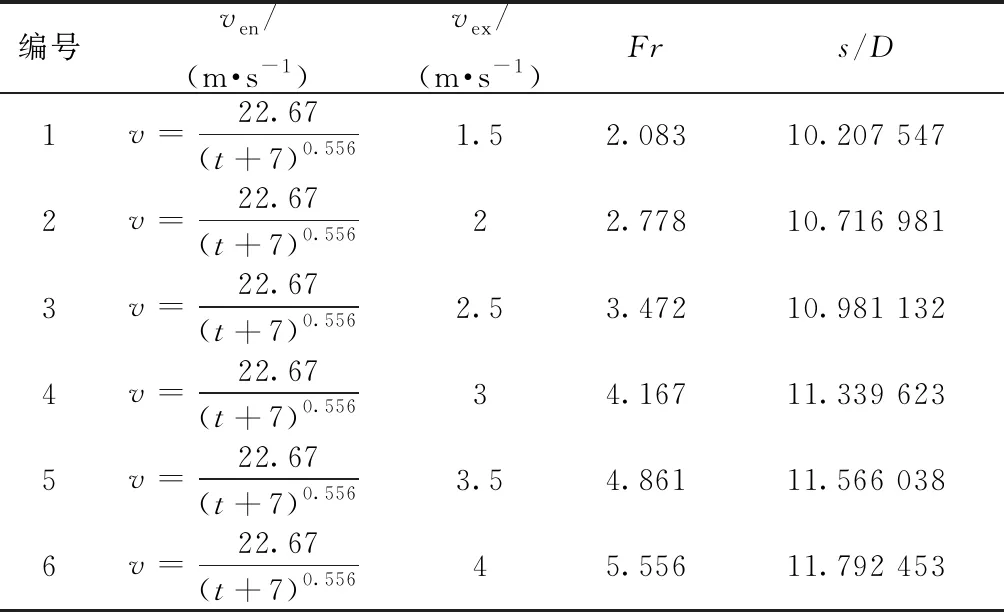
表3 入口速度连续变化条件下工况设定与后处理结果Table 3 Working condition settings and post-processing results with the input velocity being fixed

在入口速度不同的条件下，临界淹没深度较为稳定，趋于平缓，这是由于起始状态时涌入集水坑内的水流速度较大，在集水坑壁、管壁、汇水水流流场和管壁上飞溅水流流场的联合作用下，在整个水体的分布空间上半段引起的了大波动，不同速度矢量汇集下，较快地形成了涡旋。

由表3拟合得到临界淹没深度与弗劳德数之间的关系式为

s/D=0.45Fr+9.4

(23)

将拟合结果与以往学者的研究结果进行对比分析，得到结果如图8所示。从总体趋势上来讲，本文模型同样与Hecker公式较为接近，这是由实验条件的客观因素决定的；本文模型结论与文献[19]公式得到的斜率较近，说明计算流体动力学得到的结论与试验结果之间较为一致，在常数项上的区别主要是由于管径大小不同使拟合曲线整体上移，其次是由于悬高、管后壁距等参数不相同，管道服役对象的不同是结果存在差异的主要原因；与Knuass公式相比，两曲线在Fr=5.556时有交点，此时临界淹没深度基本相同，在此之前模型拟合的函数值均比Knauss经验公式高，这表明Knuass经验公式在弗劳德数达到某一定值之前时，模型的拟合曲线更为精确。

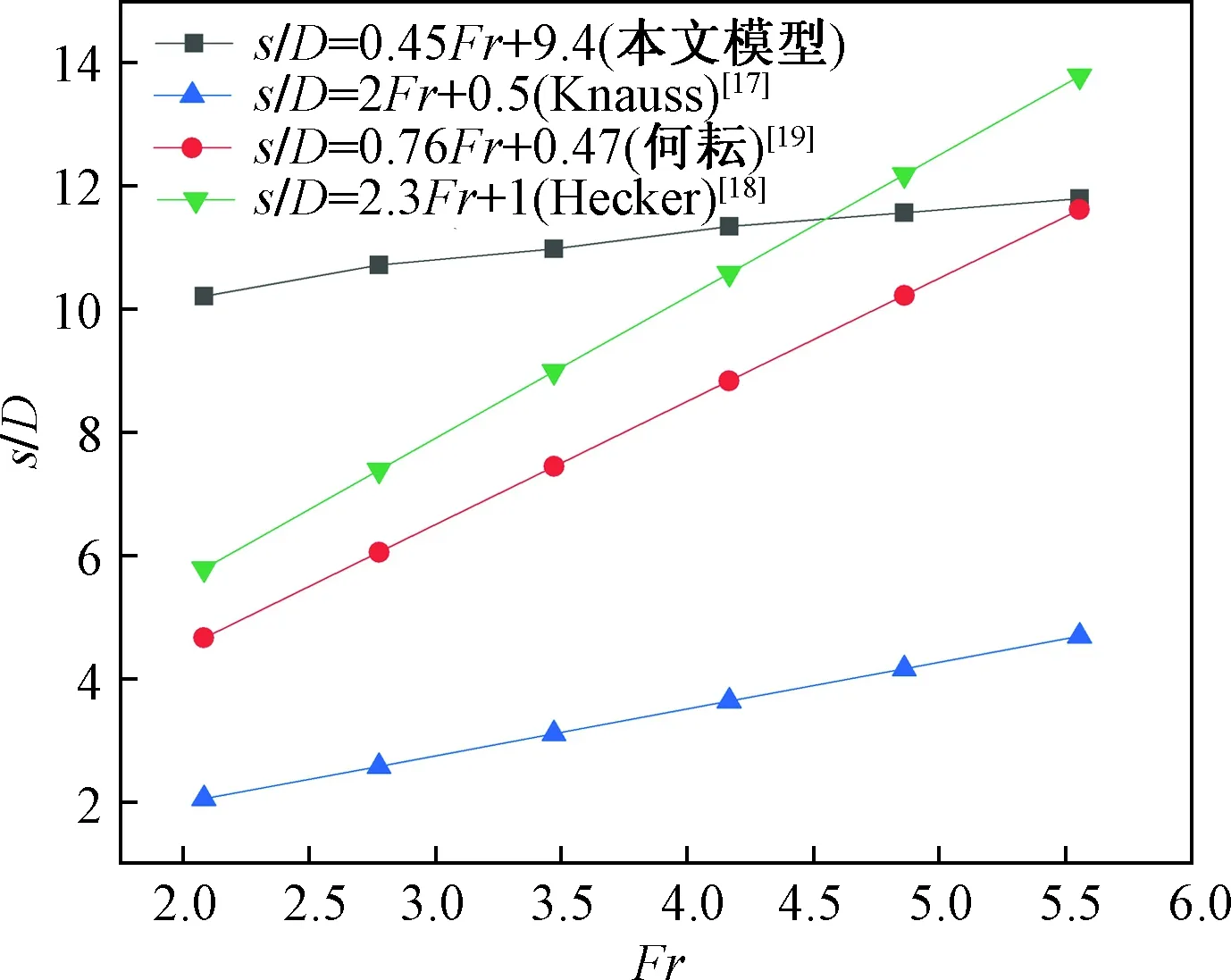
图8 入口速度连续变化条件下临界淹没深度与弗劳德数关系Fig.8 The relationship between critical submerged depth and Froude number under continuous change of water inflow velocity

5 结论

综合管廊排水系统潜水泵的临界淹没深度随着有无入口速度、入口速度恒定和入口速度连续变化而产生变化，提出了一个新的三种工况下临界淹没深度与弗劳德数之间的经验公式。与常见的三种经验公式(Knuass公式、Hecker公式和何耘公式)对比分析表明，不论在何种工况下，得到的曲线均趋近于Hecker经验公式。三种工况下拟合得到的公式可依据工程实际的不同而进行选取，为管廊排水系统集水坑的设计、潜水泵的布置与安全评价的决策提供指导性意见。