基于三维扫描的钢筋混凝土梁受力状态反演方法

郭杰明, 周 银, 尚 栋, 赵振平, 高 宇, 高洪闻, 应春莉, 韩达光

(1.重庆交通大学土木工程学院， 重庆 400074； 2.中交一公局第七工程有限公司， 郑州 451450； 3.重庆鲁汶智慧城市与可持续发展研究院， 重庆 401135； 4.奥斯陆城市大学技术&艺术与设计学院， 奥斯陆 0130)

桥梁结构在长期动、静荷载以及自然老化作用下，结构的累积损伤会影响到桥梁的表观变形，因此，可以认为结构表观几何状态的变化是桥梁结构安全预警的关键指标及依据[1]。

桥梁安全预警及健康诊断主要通过获取其相应部位的应变值以及位移变化进行诊断与评估。在位移测量方面，无论是传统方法还是新型智能系统如机器人监测法、GPS法以及水准高程法等，均是对少量观测点的数据进行拟合，难以获取结构连续挠度线型[2]，而且桥梁结构因光照、温湿度等环境因素的改变而发生变形，测量数据的准确性难以保证；在应变测量方面，传统检测方法通过表贴应变片、埋设传感器等进行数据采集、健康诊断，对于特殊部位，检测设备难以到达，且传感器、应变片等使用寿命较短、费用高、监测结果不能覆盖全局，而且需要布线进行数据接收，对于跨江跨河等特殊部位难以到达，一旦损坏，测试结果的科学性将难以保证，而人工检测需要耗费大量的人力、物力资源。

近几年三维激光扫描技术的兴起，有效改善了这一问题，因其能够快速高效地获取结构原始点云数据而被广泛应用于变形监测领域[3-5]，通过与有限元仿真技术的结合，形成了对桥梁结构的无损非接触检测的新方法和新技术思路。向小菊等[6]将车载三维激光扫描仪应用于桥面几何形态数据的采集，打破了传统桥梁变形监测仅有数个独立点的局限性，扩大了监测范围，同时提高了变形监测的精度。邓晓隆[2]采用三维激光扫描技术对一拱桥模型实现了全过程的变形监测，并将实测数据与有限元理论计算数据对比分析，证明了利用三维激光扫描技术获取点云数据精度的可靠性。崔冬蕾等[7]利用三维激光扫描技术获取结构真实挠曲线，并通过数学推导反求出结构等效荷载，将等效荷载作用下的结构响应作为梁在现状下的受力状态。Kang等[8]将激光扫描与有限元技术相结合对钢梁应力进行估算，无需在目标结构上布置传感器即可对结构响应进行评估。

基于此，现以实验室简支梁为研究对象，采用三维激光扫描技术采集准静态荷载试验数据，准静态桥梁荷载试验是诊断性荷载试验，荷载较小，不会对结构受力性能产生影响，并采用有限元正分析的位移反分析方法反演结构弹性模量、结构现状下受力状态以及重点监测部位应变值，弥补传统方法的不足，探索一条新型结构健康监测的有效替代方法。

1 基于三维扫描的钢筋混凝土梁受力状态反演方法

1.1 技术路线

以实验室简支梁加载实验为数据来源，运用三维激光扫描技术获取钢筋混凝土梁表观三维可视化模型，并通过理论建筑信息模型(building information modeling,BIM)结合成桥数据模拟结构实际初始状态，通过结构加载后变形与初始状态对比，以变形反推结构受力状态，弥补了传统方法布设传感器的不足。具体技术路线如图1所示。

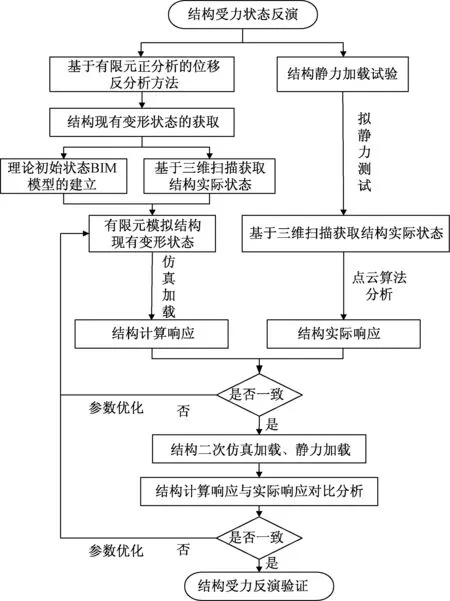
图1 技术路线Fig.1 Technical route

1.2 基于三维扫描的结构变形状态提取

1.2.1 数据采集

摒弃传统的多次设站采集方式，数据采集采用不动站扫描，避免多站数据拼接带来的误差，有效地保证了多期数据对比的可靠性，提高了结构变形提取的精度。

1.2.2 数据处理

对通过三维激光扫描技术采集的原始数据进行降噪处理，去除模型中的孤立点及噪声点，增加模型平滑度的同时又不影响其原始特征[9]。

对经过降噪处理的数据进行变形状态提取，采用改进的滑动窗口算法(图2)以及最小二乘算法处理点云数据，改进的滑窗算法通过控制窗口网格尺寸以及可移动节点位置进行数据的快速分类及处理[10]，同时具备滑窗算法及跳窗算法的功能，根据数据不同处理要求可以采用如下三种模式：模式a：窗口1(黑)-窗口2(绿)-窗口3(红)；模式b：窗口1(黑)-窗口3(红)-窗口4(黑)；模式c：窗口1(黑)-窗口4(黑)-窗口6(黑)。

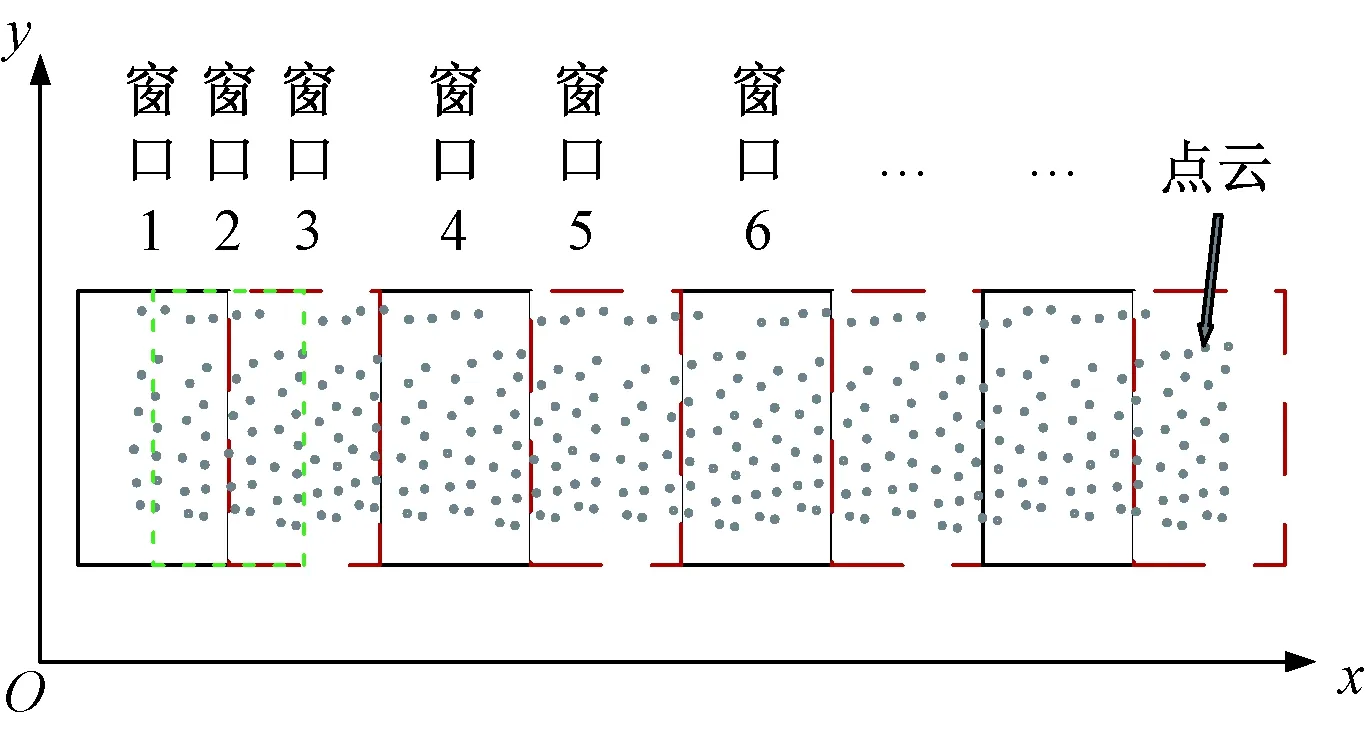
图2 改进的滑动窗口算法示意图Fig.2 Schematic diagram of improved sliding window algorithm

为了保证结构变形曲线的连续、平滑及精确性，采用模式a处理点云数据，具体流程如下。

(1)提取结构重点监测部位点云数据。

(2)计算边界最值xmin及xmax确定监测部位尺寸信息L。

(3)确定监测点间距Δ及监测点位置xi。

(1)

(4)根据监测点数量确定窗口网格尺寸d。

(5)搜寻监测点窗口范围内数据，并把每个窗口内数据设定为一个元胞数组Ci，元胞数组Ci内数据应满足：

(2)

(6)计算监测点纵坐标zi。

(3)

式(3)中：D为监测点坐标矩阵；m为元胞数组中点的个数。

(7)采用最小二乘算法进行数据拟合并绘制变形曲线。

1.3 基于有限元正分析的位移反分析方法

1.3.1 结构现有变形状态的获取

为获取结构现有变形状态，故需采集其初始状态以及现有状态数据，通过两者的对比从而获取变形数据。可通过三维激光扫描技术快速获取结构现有状态可视化三维数据，但由于客观因素影响，其初始状态数据可采用以下两种方式获取：方法①：通过三维激光扫描技术获取其初始数据；方法②：对于老、旧结构，已不具备使用三维激光扫描技术采集其初始数据，故采用BIM技术配合其成桥监测数据模拟其初始状态(图3)。运用BIM技术的三维可视化信息以及快速参数化建模的特点，依据二维图纸建立三维可视化信息模型，并配合成桥线型监测数据，通过调整BIM模型中每一节段参数信息，构建出结构初始状态，通过方式②构建的结构初始状态与后期扫描模型基于不同坐标系，故需采用坐标配准方法进行坐标系的统一。目前解决该问题多采用标定物拼接、最近迭代算法以及特征点配准方法，标定物配准方便、快捷，但难以在BIM模型中确定与实际模型对应的标定位置；最近迭代配准算法精度较高，但由于需经过多次迭代耗时较长，若初值选取不合适，会影响其迭代速度以及收敛效果[11]；该实验采用特征点配准方式，分别在BIM模型与后期扫描点云模型中查找至少三对不共线且不在结构同一平面内的对应公共点，通过矩阵平移旋转算法计算其6个自由度[12]，即3个平移变量(x，y，z)以及3个旋转变量(Rx，Ry，Rz)。

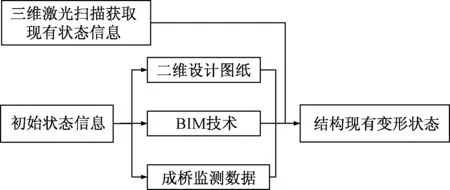
图3 技术路线Fig.3 Technical route

1.3.2 现有实际状态的模拟

在获取结构现有变形数据基础上，以有限元模型的位移响应为参考，施加结构自重以及当前所处荷载条件，使得结构计算响应与实测响应一致，从而模拟结构实际状态。考虑到混凝土结构大多处于带裂缝工作状态，且其在极限状态下会表现出材料非线性特性，采用MIDAS FEA分析软件对结构进行考虑材料非线性的分析，混凝土本构为总应变裂缝模型，受拉裂缝模型为线性模型，受压裂缝模型为Thorenfeldt模型，同时忽略横向裂缝及约束的影响，采用牛顿拉普森(Newton Raphson)迭代法进行计算[13]。

1.3.3 结构参数反演分析

选取结构的弹性模量和外荷载为待识别参数，结构位移为量测信息，当理论计算值与相应的测试值达到最大限度的吻合时，即认为该组参数是结构当前状态的参数。结构参数反演步骤如下。

(1)通过修正后的初始状态BIM模型与三维激光扫描获取的当前状态点云模型对比得到结构当前变形模式。

(2)根据结构理论特性参数、约束条件等建立有限元模型。

(3)假设结构自重和外荷载F为当前所受荷载，混凝土材料弹性模量E为理论值,边界条件为实际所处约束状态，按非线性静力分析，以位移标准计算收敛，最终提取结构位移(w0)曲线。

(4)调整外荷载F使得计算位移(w0)与实测位移(w1)相等。

(5)在有限元模型与实际结构上继续施加相同大小荷载F1，此时结构所受荷载为(自重+F+F1),对比此时理论计算位移w2与实测位移w3，若w2≠w3，返回第(3)步重新调整弹性模量E与外荷载F进行计算；若w2=w3，继续施加外荷载F2，同时对比理论位移响应w4与实际位移响应w5，若两者相等，则当前模型假设荷载F及混凝土弹模E即为当前实际状态值，当前有限元模型即可反映结构实际状态，可通过理论模型分析重点监测部分应力数据以及判断结构承载力；若两者不等，返回第(3)步重新调整参数，直至w4=w5，则计算结束。

2 实验及数据分析

2.1 实验概况

为验证该方法的可靠性，设计钢筋混凝土简支梁加载实验进行验证，梁截面为矩形且为适筋梁，梁截面尺寸150 mm×300 mm，梁长4 400 mm，计算跨径4 000 mm，混凝土设计强度为C25，钢筋采用HRB335级钢筋，实验梁截面尺寸及配筋如图4所示。实验数据采集如图5所示，主要量测信息如下。

(1)挠度。从跨中位置向左右每隔40 cm布置百分表，共计11处，百分表量程1 cm，精度0.01 mm。同时在梁底架设三维激光扫描仪，实验仪器采用徕卡Scanstation P50扫描设备，扫描速率高达1 000 000点/s,最远距离1 km，最高支持0.8 mm@10 m的扫描分辨率，满足复杂环境下数据采集的可行性及可靠性，本次数据采集设置270 m模式下扫描精度为1.2 mm。通过百分表量测的挠度值验证扫描仪变形监测的精度。

(2)荷载。通过液压千斤顶在跨中部位施加荷载，由荷载传感器监测荷载数值，传感器额度容量20 t,综合精度C4等级，可识别最小单位为5 kg，千斤顶及传感器设备自重为20 kg。

(3)应变。分别在梁端、1/4跨、1/2跨部位沿高度方向各布置5片应变片，为消除外界温度影响，在梁端布置温度补偿片，应变片为BX120-50AA混凝土应变片，应变极限为2 000 με。同时采用DH-3818静态应变测试仪采集数据，选用1/4桥接线方式，多通道共用补偿片。

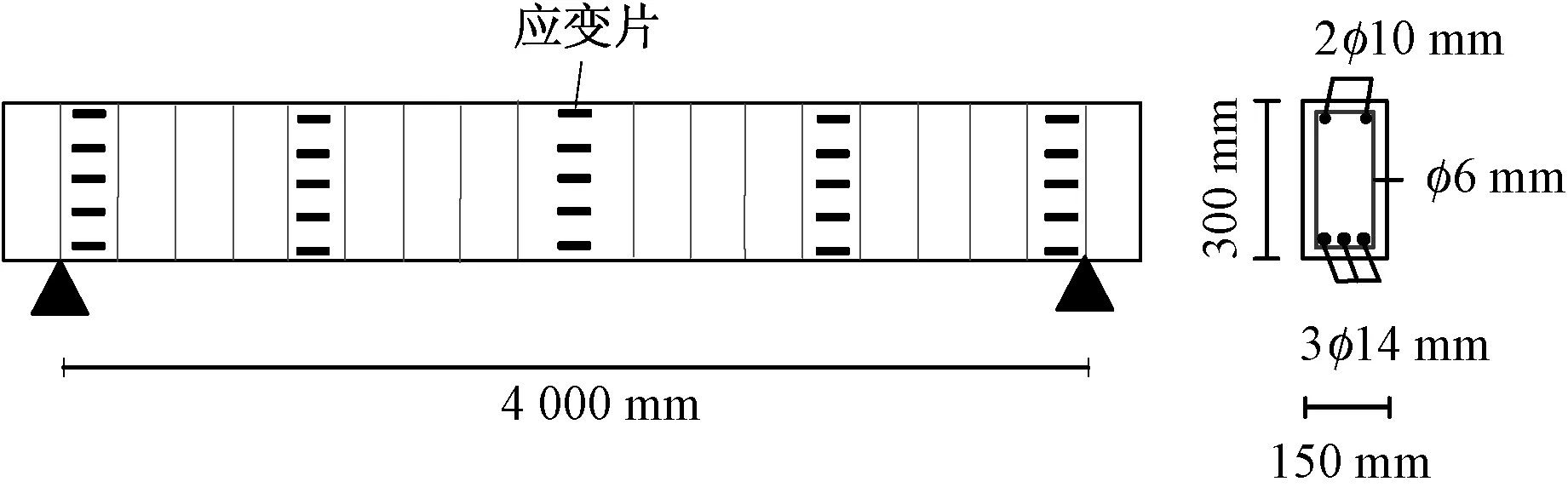
图4 梁纵截面(左)及横截面(右)图Fig.4 longitudinal section (left) and cross section (right) of beam

2.2 实际变形状态提取

2.2.1 初始状态BIM模型的建立

由1.3.1节可知，结构实际变形状态可通过两种方法获取:①借助三维激光扫描仪采集原始数据及后期各项数据;②采用改进滑窗算法及最小二乘法处理点云即可获得变形状态。本次实验采用第②种方法即借助BIM技术及成桥监测数据模拟初始状态(图6)，后期数据通过三维激光扫描技术获取，同时将BIM模型转换为点云模型，对各期数据对比求取变形数据。

图5 实验数据采集Fig.5 Experimental data collection

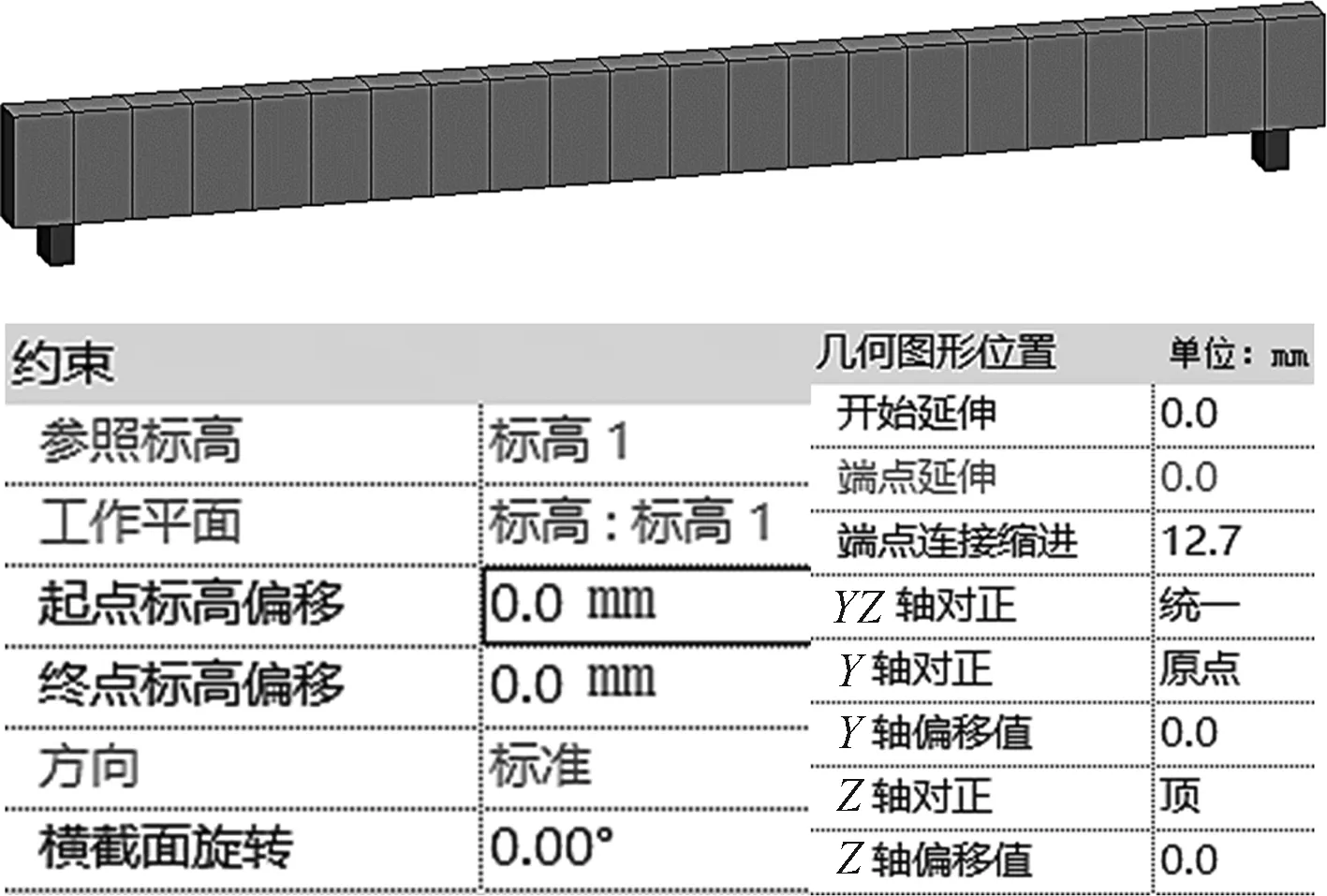
图6 BIM模型及可调参数Fig.6 BIM model and adjustable parameters

2.2.2 模型配准及变形提取

选取结构外相对稳定部位作为配准特征点，如支座角点，对三个两两相交的平面进行拟合，如图7所示，其交点坐标即为特征点坐标。以BIM模型为基准数据，将后期点云模型进行配准。

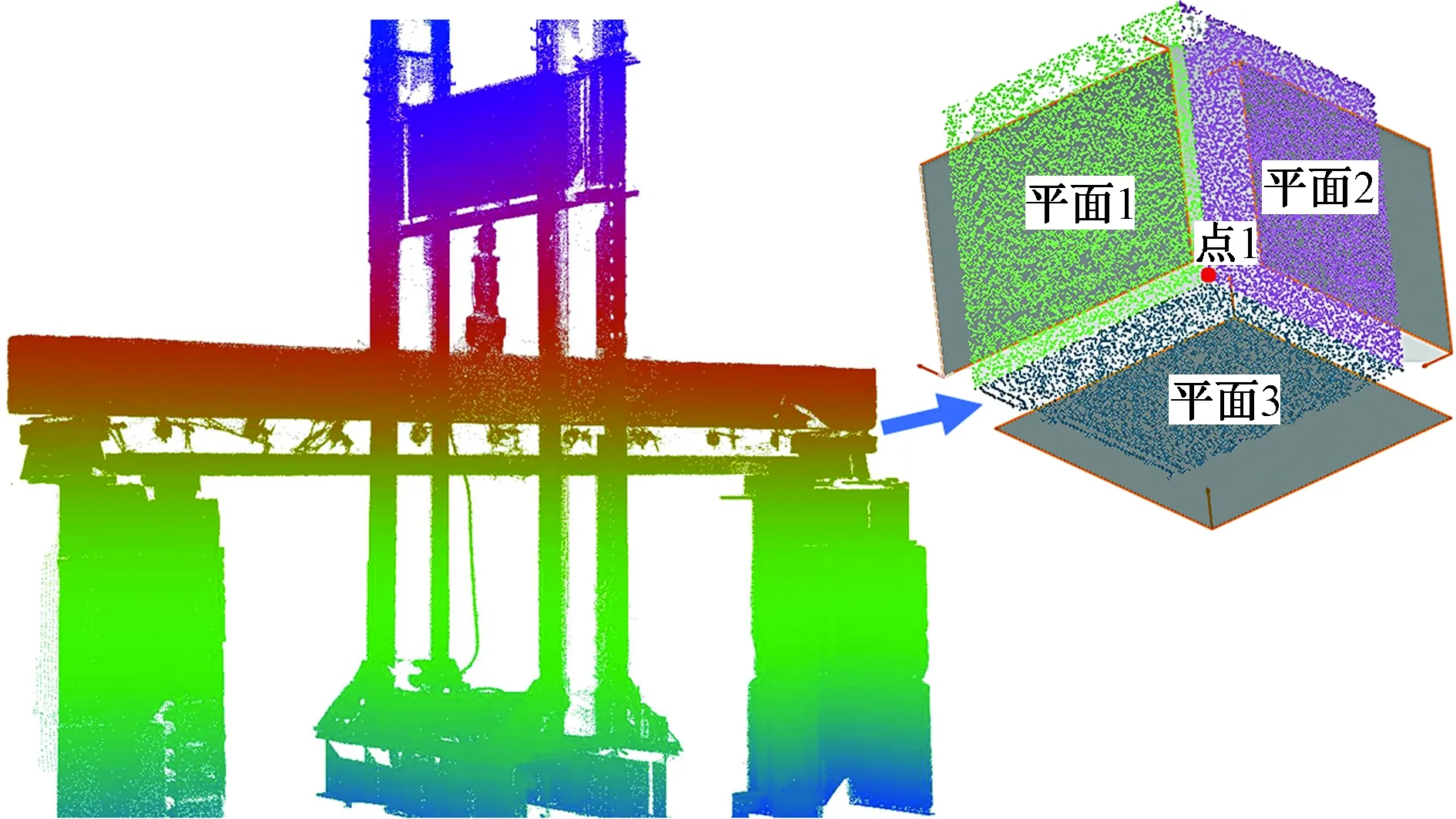
图7 实验梁点云(左)及支座处特征面拟合(右)Fig.7 Point cloud (left) of experimental beam and feature surface fitting at support (right)

数据配准精度决定后期变形结果提取的准确性，从而直接影响结构受力状态反演的效果。数据配准结果如表1所示，可知最大偏差为0.000 59 m，且重点关注方向Z向偏差整体偏小，均在0.5 mm以内，保证后期变形提取的准确性。

实验为准静态加载，共加载三次，以第一次加载模拟结构现有受力状态，第一次加载所得数据为结构受力反演对象，后两次加载对所反演的第一次数据参数进行验证，荷载工况如表2所示。

设定监测点间距为0.15 m，滑窗尺寸0.2 m，即1.2.2节的模式a采集数据，采用最小二乘法绘制变形曲线，如图8所示，由百分表测量所得变形曲线与三维扫描监测曲线相比最大误差为0.2 mm以内，在变形监测应用上达到亚毫米级精度。

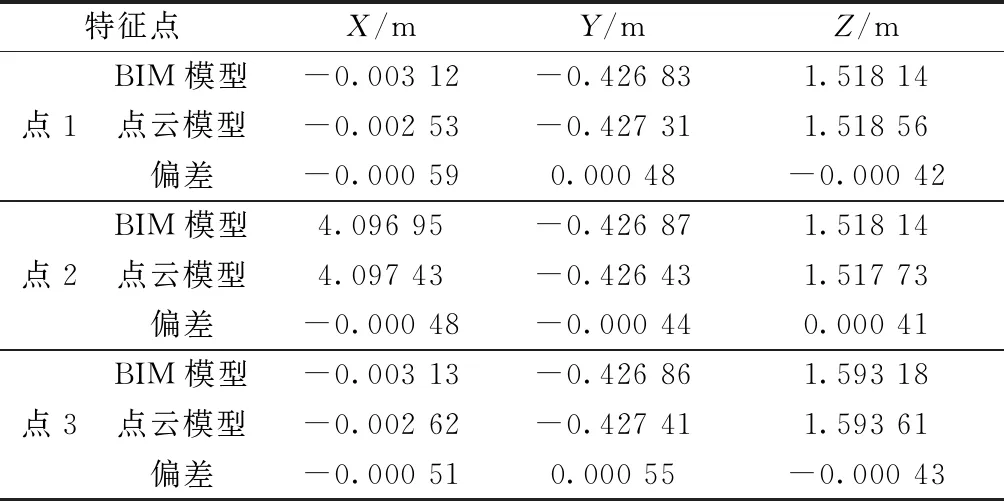
表1 特征点配准结果Table 1 Registration results of feature points

表2 实验荷载工况

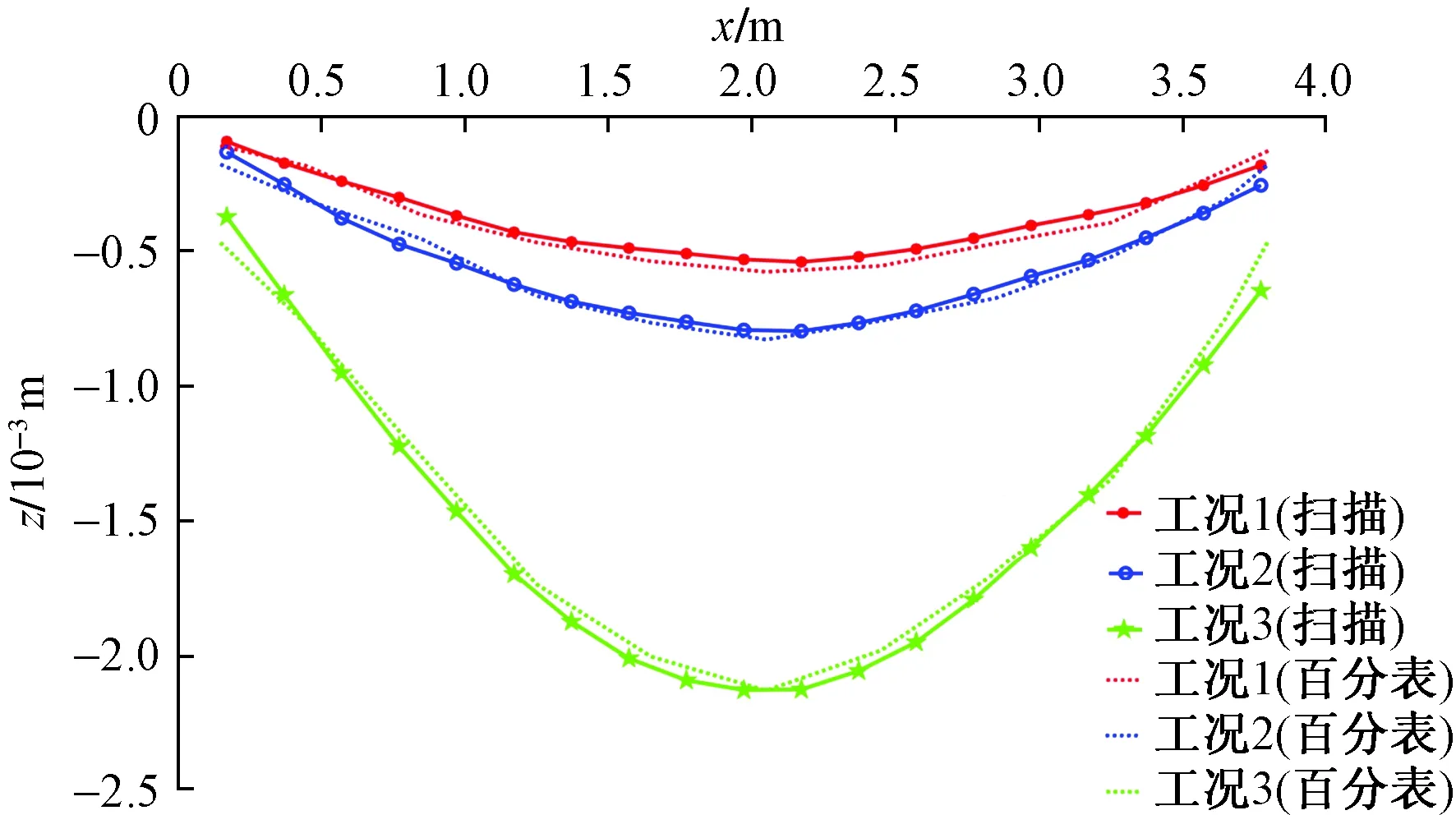
图8 变形曲线Fig.8 Deformation curve

2.3 位移反分析法求解结构受力状态

按理论计算弹性模量进行有限元仿真模拟，如图9所示，施加荷载使其位移响应与实测值一致，并按照1.3.3节结构参数反演步骤求解。

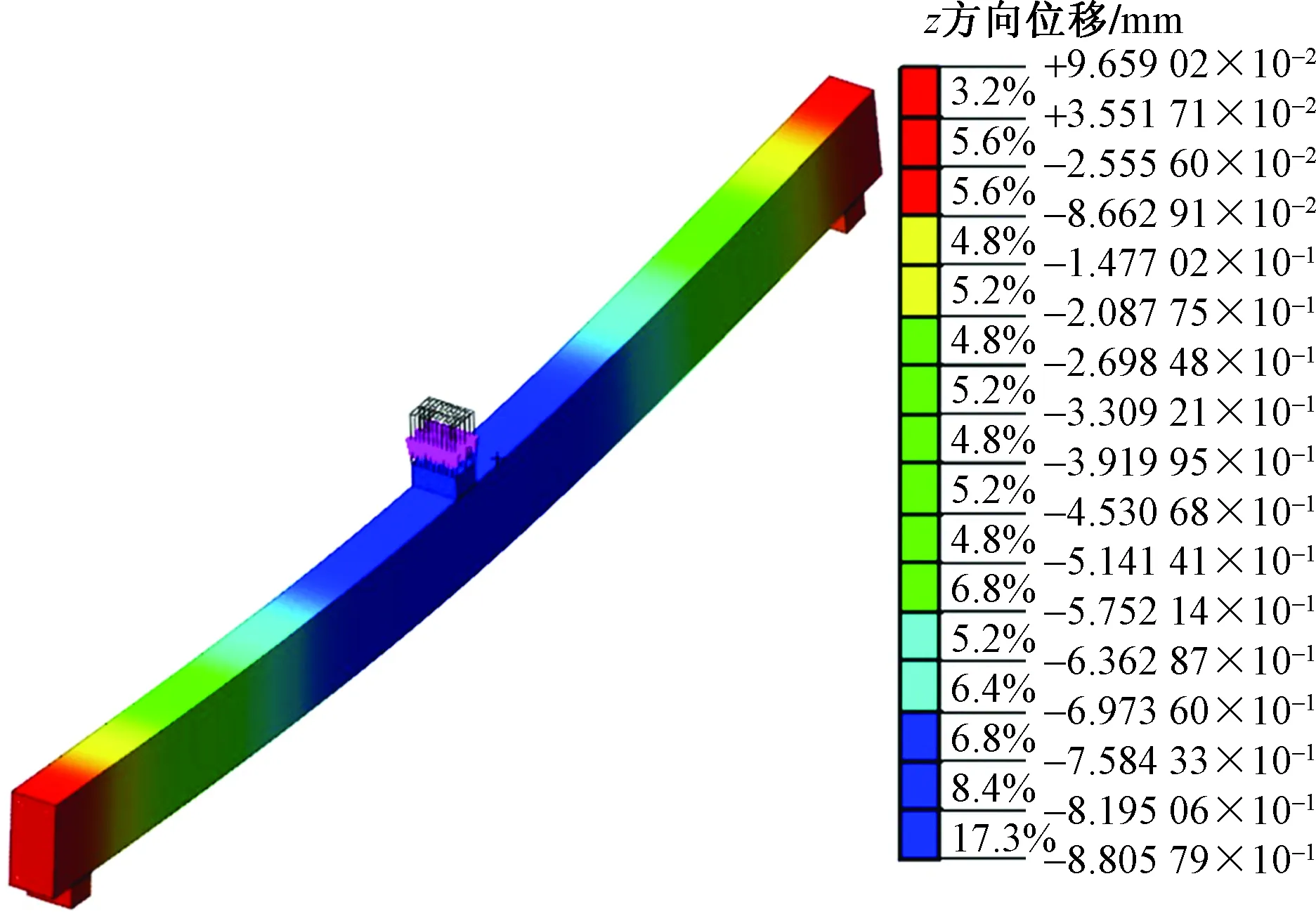
图9 有限元仿真变形Fig.9 Finite element simulation deformation

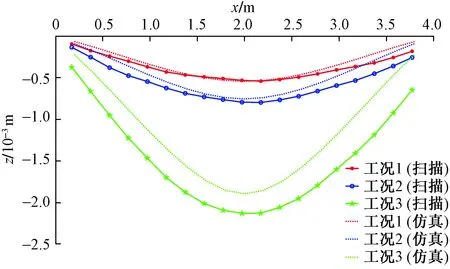
图10 理论与实测曲线对比Fig.10 Comparison of theoretical and measured curves

由图10可知，所反演工况1的参数作用下结构实测位移与理论位移响应一致时，工况2和工况3计算位移均小于实测值，表明结构弹性模量低于理论值，所反演工况1的荷载并不能反映结构实际受力状态，故需对反演参数重新优化。

通过建立弹性模量、所施加荷载以及跨中最大位移的函数关系进行参数反演，结果如图11所示。该函数关系及三维曲面的表达式为

z=f(x,y)

(4)

(5)

式中：x为结构弹模；y为所施加荷载；z为跨中位移。其中,工况1、工况2、工况3跨中位移z1、z2、z3可通过三维扫描变形曲线获得，而y1、y2、y3之间存在一定关系，故未知数仅为x以及y1，通过三个表达式即可求解。

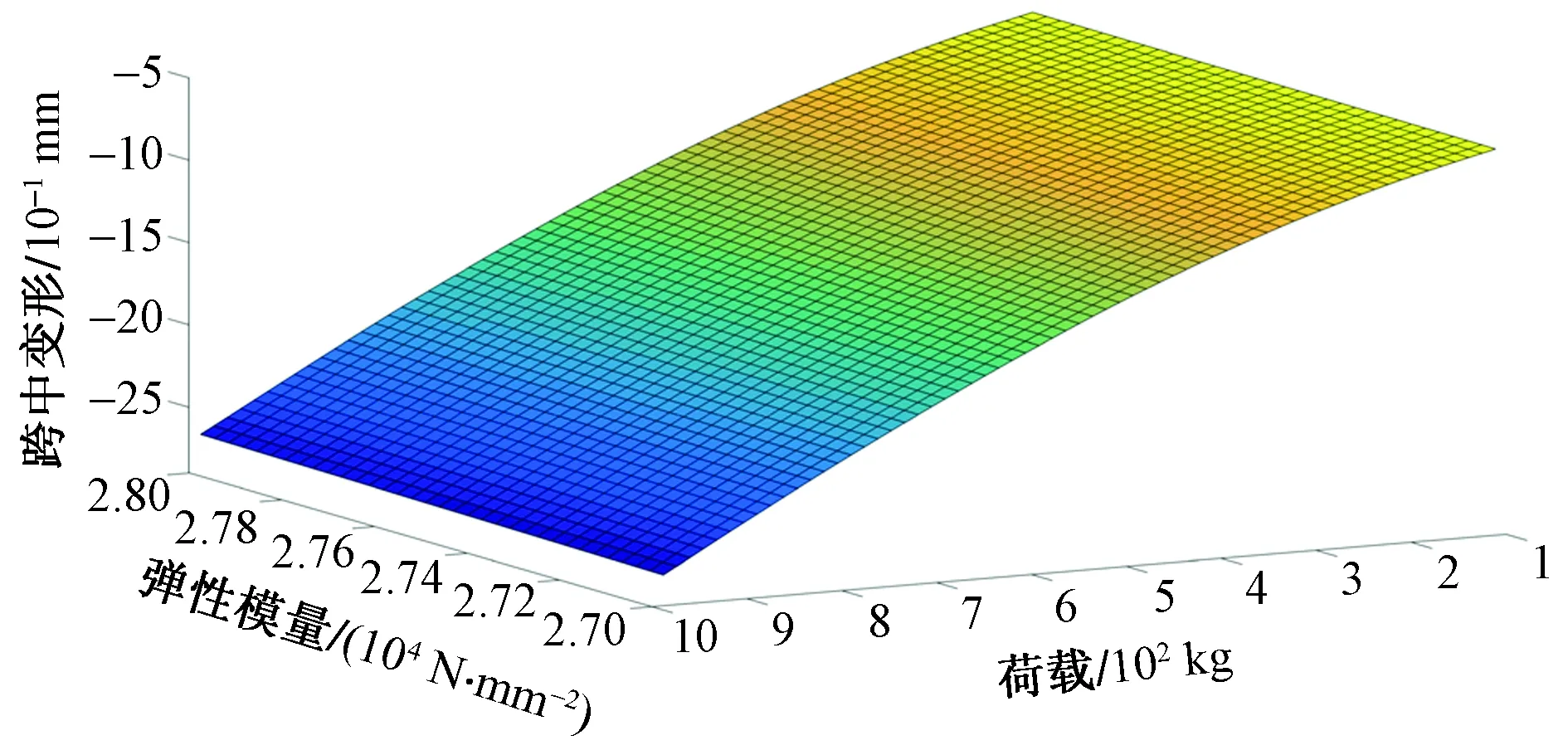
图11 参数反演曲面Fig.11 Parameter inversion surface

z(x,y)=p0+p1x+p2y+p3x2+p4xy+p5y2+

p6x3+p7x2y+p8xy2+p9y3

(6)

参数值依次为：p0=-319.7,p1=338,p2=-3.688,p3=-121.3，p4=1.81，p5=-0.196,p6=14.55,p7=-0.267，p8=-0.005,p9=0.0054。

由参数反演表达式(6)求得结构弹性模量E=27 512 N/mm2,所施加外荷载y1=128.97 kg。同时，从变形曲线可看出反演位移与实测位移基本吻合(图12)。

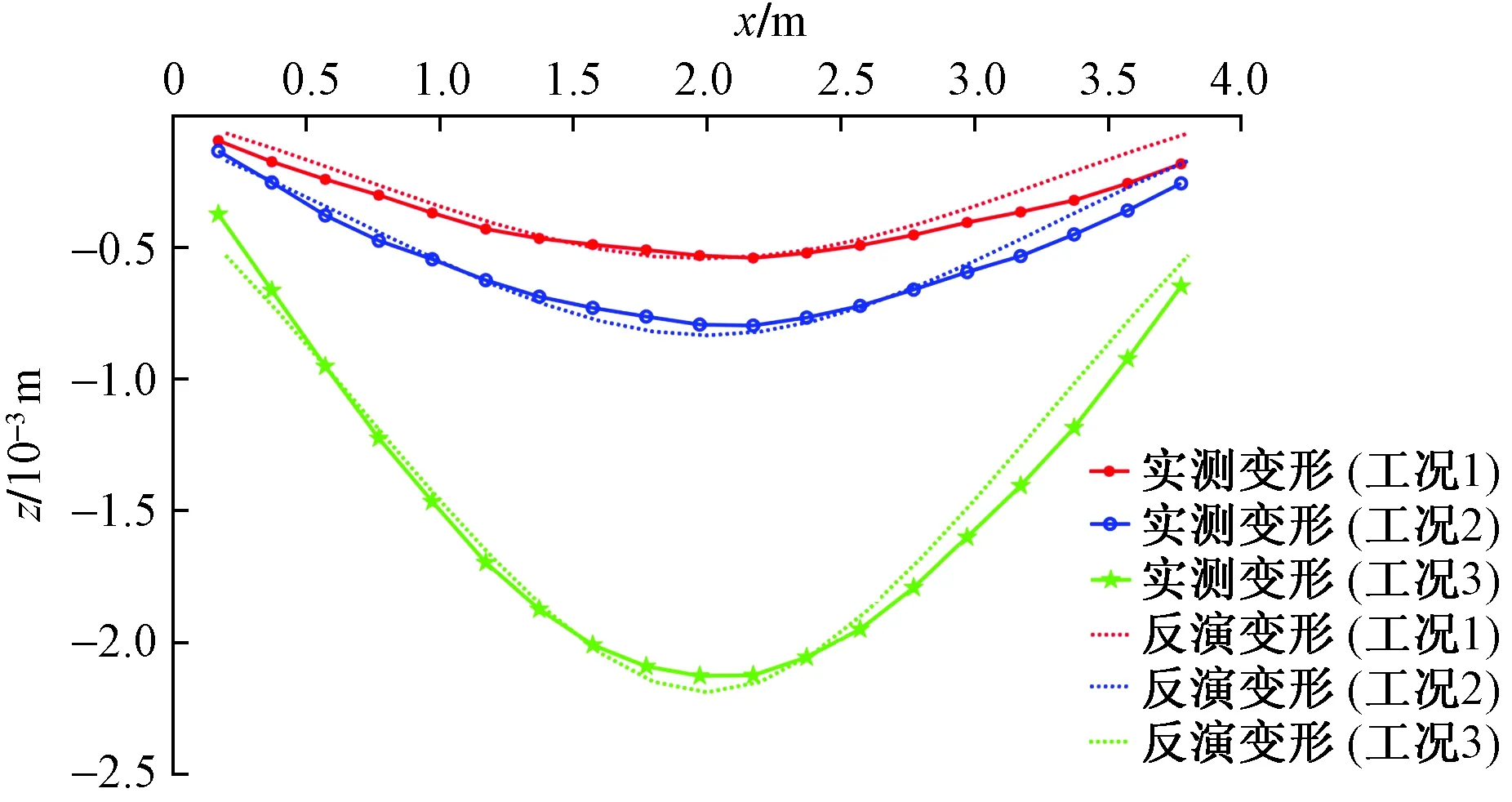
图12 反演结果与实测结果对比Fig.12 Comparison between inversion results and measured results

3 结构受力状态反演验证

根据图12曲线对比结果，定性地评估结构受力反演效果，分别从反演荷载以及应变两方面进行定量评估。

(1)荷载反演对比：根据图11曲面表达式进行求解的工况1中外荷载即结构受力反演荷载为128.97 kg，与实际值误差为0.79%。

(2)应变反演对比。以梁上、下边缘实测应变与反演计算应变对比评估结构内力反演效果，如表3所示。

从整体效果看，反演荷载值与实测值误差较小，

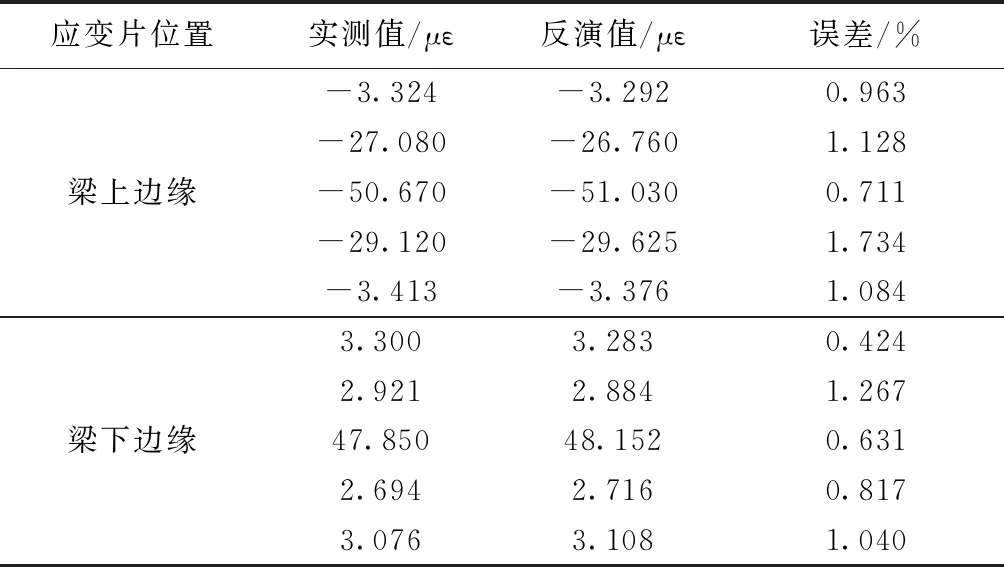
表3 实测应变与反演应变对比

而个别应变与实际值误差略大，分析可能由如下原因导致：应变片粘贴不规范，留有气泡；结构表面未打磨平整；应变片胶层过厚；读数时，静态应变测试仪数据不稳定，出现波动等。可从以上几方面改进实验从而提高数据可靠性。

4 结论

提出了一种基于三维激光扫描技术的无损非接触的新型桥梁结构健康监测方法，并以实验室简支梁加载实验进行验证，得出如下结论。

(1)数据处理方面，采用改进的滑窗算法灵活调整监测点位置及窗口尺寸，提高了数据采集及分析的效率，同时采用最小二乘法对所提取数据进行拟合，保证了变形曲线的连续性及平顺性。

(2)变形监测方面，采用不动站扫描方式采集数据，并通过算法自动计算变形结果，同时与百分表采集结果对比分析，表明三维激光扫描监测变形精度达到亚毫米级别。

(3)受力反演方面，采用有限元正分析的位移反分析理论，以变形结果反演结构现状下受力状态参数，无需布设传感设备，实现无损非接触检测，解决了跨江、跨河等特殊部位数据采集困难的问题，对于桥梁结构的健康监测与诊断具有重要理论意义与实际价值。