基于神经网络的切换非线性系统辨识

王 林, 王宏伟,2*, 柴秀俊

(1.新疆大学电气工程学院， 乌鲁木齐 830047； 2.大连理工大学控制科学与工程学院， 大连 116024)

切换系统是由一系列有限个子系统和决定子系统之间相互联系的规律(切换规律)组成的混杂系统。作为一类非常重要的混杂系统，切换系统广泛存在于人们的生活中。比如汽车的变速箱系统中，加速、减速、匀速等对应发动机输出的转速比是不同的，即不同运动阶段汽车的动力系统模型不同。此外，电力系统[1]、机器人控制系统[2]、温度控制系统、搅拌反应釜系统[3]、复杂网络同步系统[4]、多智能体系统[5-9]等依然存在着大量的切换系统。

对于切换系统辨识，一般需要利用采样数据辨识切换规律和系统参数。由于切换规律作用，切换系统数据通常是混杂的，采样数据与各个子系统的对应关系通常是未知的，普通辨识方法很难保证切换规律辨识的准确率和参数辨识算法的鲁棒性。为解决上述问题，学者们进行了多方面研究，在切换线性系统情况下，Sadeghi等[10]引入了引力搜索法、Juloski等[11-12]引入了贝叶斯算法、Wang等[13]提出了增益重置策略、Borges等[14]引入了投影子空间法、Bako[15]提出了凸优化法、Ma等[16]提出了混合整数规划法、Sefidmazgi等[17]提出了聚类法。

以上研究主要集中于线性系统领域，由于非线性系统本身具有非线性、复杂性和多样性，采用线性辨识方法一般不能解决切换非线性系统的辨识问题。因此，一些学者展开了此方面的研究。Zhang等[18]对于连续电机伺服转台系统，提出了一种切换非线性自回归滑动平均(nonlinear auto regressive moving averagee xogenous，NARMAX)模型，将转台NARMAX模型的切换规律和参数辨识转化为约束多目标优化问题(constrained multiobjective optimization problem，CMOP)，并提出使用Pareto最优多目标粒子群优化算法解决上述CMOP问题。Bianchi等[19]引入范畴分布和伯努利分布，通过调整每个子系统模型的概率分布，逐步获得趋向整体混合模型的极限分布，最终获取最优切换模型。此算法在模式分配和模型识别方面都有很好的表现，但存在因陷入局部问题而造成模式识别不匹配现象。Bianchi等[20]又针对一类切换非线性自回归模型提出了一种两阶段黑箱迭代辨识法，在第一阶段中，假设模式切换只能在预定义的时刻发生，而在第二阶段中通过细化候选切换时间的数量和位置，最终估计实际模式切换。然而，这种方法精确估计的前提是需预先知道大致切换时间。

上述文献提出的辨识方法中存在切换规律识别有一些失配情况以及对切换时间存在要求，而一般情况下切换规律识别错误率越高，系统辨识结果准确度越差。基于上述讨论，针对切换非线性系统切换规律和参数难于辨识的问题，现提出基于BP神经网络和折息递推辨识算法辨识切换非线性系统模型的方法。此方法引入标签函数标签化所有子系统，利用系统采样的混杂数据，通过BP算法对神经网络进行训练，从而建立非线性系统切换规律的神经网络预测模型，利用神经网络预测模型对切换规律进行预报，目的是提高预报质量，降低识别错误率；然后，使用折息递推辨识算法和关键项分离法在线辨识非线性系统中各子系统的参数，进而解决各子非线性系统的参数辨识问题；最后，给出非线性系统辨识仿真和结论。

1 问题描述

一类Hammerstein-Wiener切换非线性系统模型如图1所示。在第k时刻，切换规律σ(k)控制系统切换至第i个子系统，此时刻系统输出y(k)由第i个子系统决定，由此完成当前时刻系统运行。

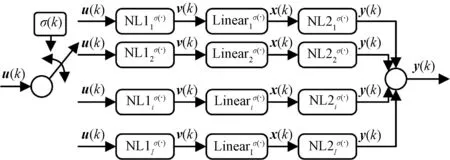
NL1i、NL2i分别为第i个子系统输入端非线性环节、输出端非线性环节；Lineari为中间动态线性环节；σ(·)为该系统切换规律，σ(k)为第k时刻的切换规律；u(k)、y(k)分别为系统输入和输出信号图1 Hammerstein-Wiener切换非线性系统模型Fig.1 Hammerstein-Wiener switching nonlinear system model

在图1中，考虑如下Hammerstein-Wiener切换非线性系统模型：

v(k)=Fσ(k)[u(k)]

(1)

x(k)=Gσ(k)(z-1)v(k)

(2)

y(k)=Hσ(k)[x(k)]

(3)

式中：σ(k)为满足σ(k)∈i={1,2,…,I}的分段切换函数；Fσ(k)(·)、Hσ(k)(·)为系统输入端非线性函数、输出端非线性函数；Gσ(k)(z-1)为系统中间动态线性环节的传递函数；v(k)、x(k)分别为第一、二个非线性系统的输出信号，v(k)∈R，x(k)∈R；u(k)∈R、y(k)∈R且分别为非线性系统的输入和输出信号。

在σ(k)切换规律的控制作用下，第i个子系统被激活，第i个子系统中的输入和输出非线性函数都用已知的非线性基函数的线性组合来描述，此时被激活的非线性子系统为

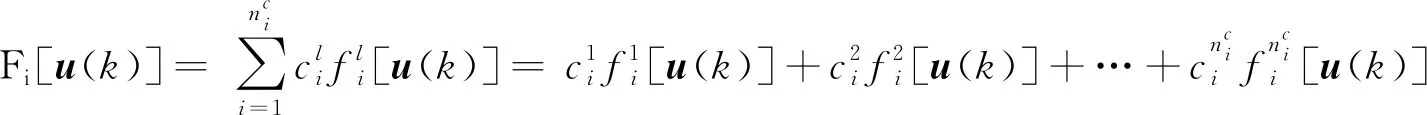
(4)

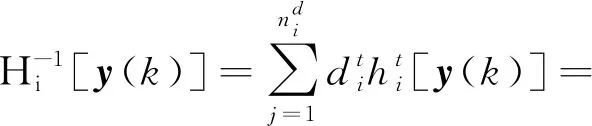
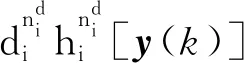
(5)

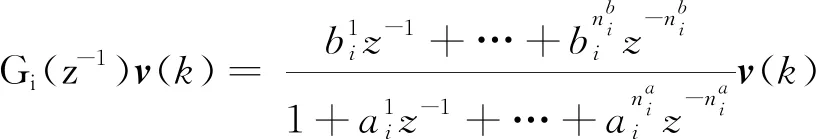
(6)

式中：

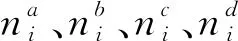
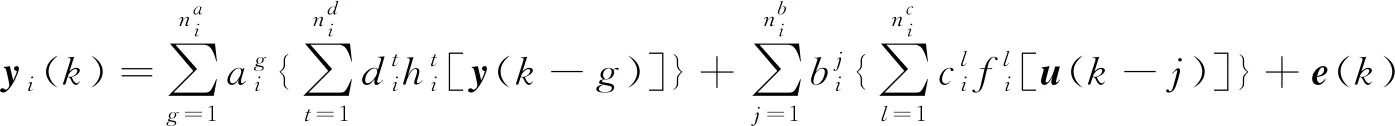
(7)

式中：e(k)为均值为零、方差为δ2的噪声。

整理式(7)可得

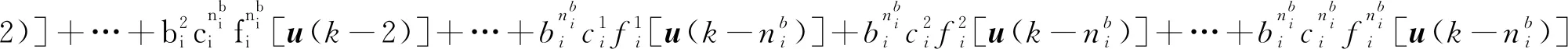
(8)

定义两向量即参数集乘积项向量ϑi和信息向量φi(k)，形式如下：

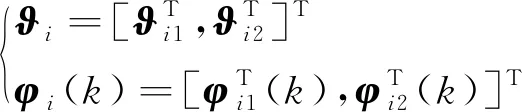
(9)

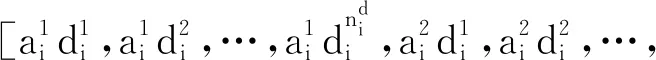
(10)

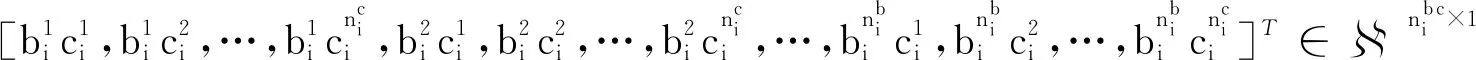
(11)

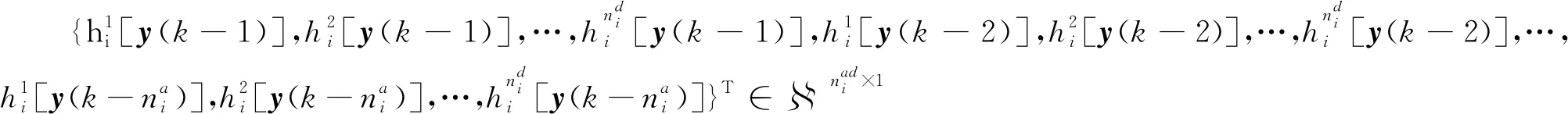
(12)

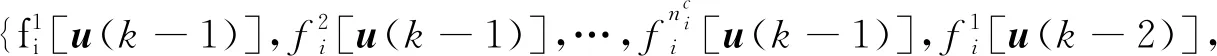
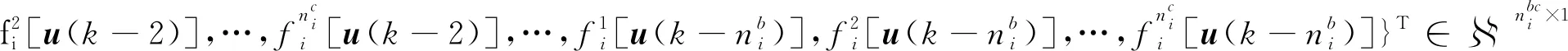
(13)

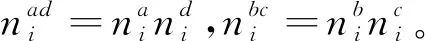
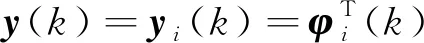
(14)

对于切换系统[式(14)]的辨识任务为两个，即切换规律σ(k)的确定和模型中参数的辨识。系统切换方式，文献[13]认为有三种，即周期切换、不定期切换和随机切换。在上述切换方式作用下，在工作时间内系统会形成切换序列[σ(1),σ(2),σ(3),…,σ(k),…]。切换规律辨识任务：估计当前采样时刻系统要切换到哪个子系统和在这个子系统上驻留的时间。基于输入/输出采样数据，建立切换规律σ(k)的神经网络预测模型和辨识模型[式(14)]中的参数。

2 切换规律预测模型建立

在切换系统辨识中，切换规律有时有些经验数据，通过对经验数据的训练和分类建立神经网络预测模型，从而实现对未知切换的子系统、切换时刻、每次切换驻留时间等信息进行预测。

2.1 标签化切换规律

为更好预测，同时便于跟踪和分析每个子系统特征，首先引入标签，统一子系统标识。在切换系统中，每个子系统都是独立且唯一的，因此每个子系统标签也必须唯一。将第i个子系统标签定义为δi，形式为

δi=[01,…,0i-1,1i,0i+1,…，0I]T

(15)

具体的，δi共有I位(I为切换子系统总数)，当切换至第i个子系统时，第i位置1，其余位置0，表示该子系统的标签被启用。当系统第k时刻切换至第i个子系统时，标签可表示为

δ(k)=[01,…,0i-1,1i,0i+1,…，0I]T。将标签引入后，系统切换规律可以用式(16)描述，即

σ(·)=δ(·)=[δ(1),δ(2),δ(3),…,

δ(k),…]

(16)

2.2 BP神经网络的切换规律预测模型建立

BP神经网络是一种多层前向神经网络，含有单个隐含层的BP神经网络结构如图2所示，其拥有R个输入神经元、M个输出神经元和O个隐含层神经元。在第k次迭代时，输入层第r个神经元、隐含层第o个神经元输出分别为x′r(k)、p′o(k)，输出层第m个神经元的实际输出、期望输出分别表示为z′m(k)、y′m(k)，输出层第r个神经元与隐含层第o个神经元之间连接的权值为w′ro，隐含层第o个神经元与输出层第m个神经元之间连接的权值为s′om。

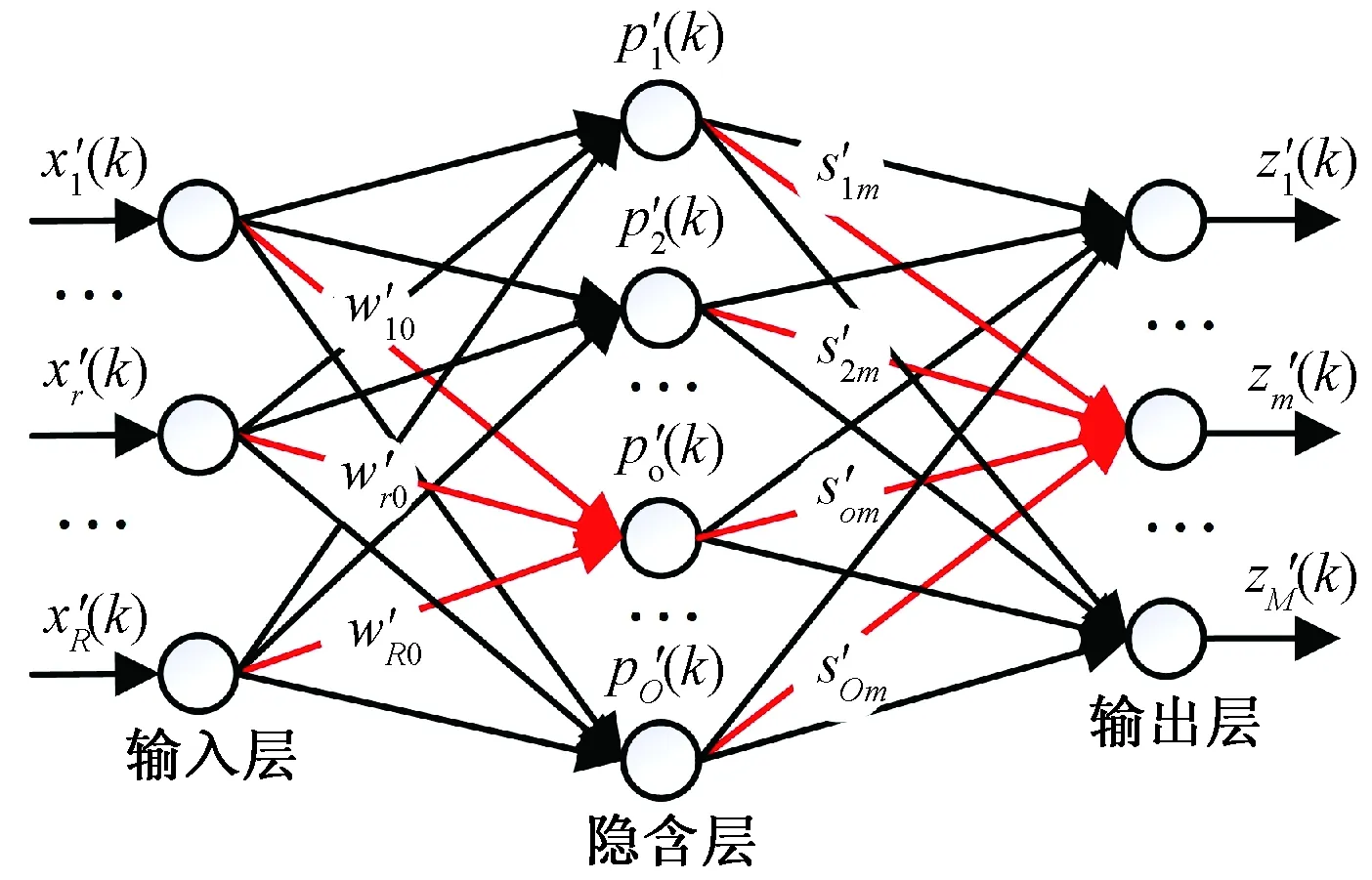
图2 BP神经网络结构图Fig.2 BP neural network structure diagram

在预测切换系统切换规律之前，首先要对BP神经网络进行训练，建立切换规律的神经网络预测模型。选取时间段[0,K]内各个子系统的状态数据组成训练集N=[X,Y]，由式(9)、式(14)、式(16)构成输入数据集X：

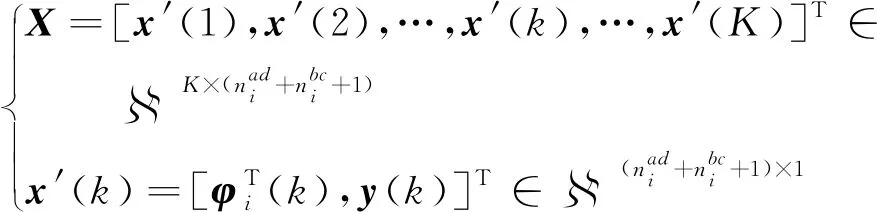
(17)

构成实际期望输出数据集Y：

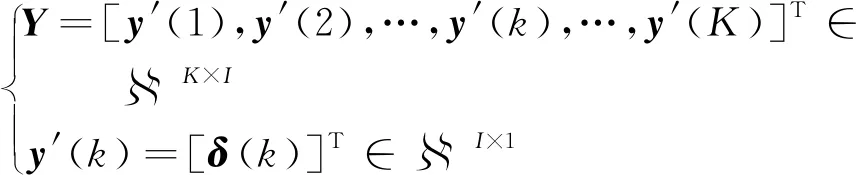
(18)

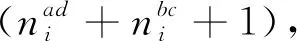
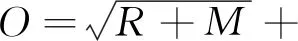
(19)

网络中隐含层激活函数、输出层激活函数分别选取logsig函数、softmax函数作为激活函数，它们函数形式如下：

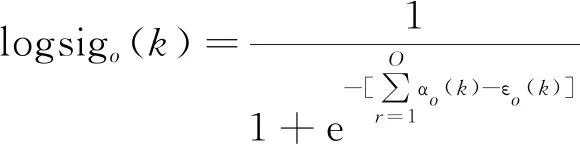
(20)

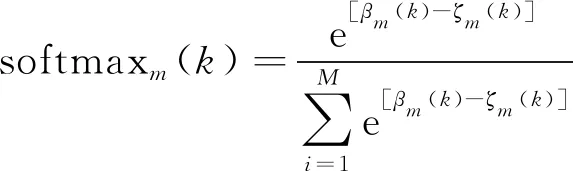
(21)

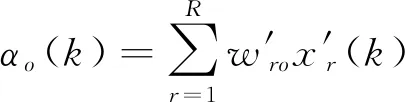
(1)给定网络的训练样本N(样本形式)和切换规律数据，设置网络参数，包括：隐含层数目O、学习率ζ、训练误差E′及网络训练次数M。

(2)初始化网络权值等参数。

(3)计算输出层输出z′m(k)以及输出层实际输出与期望输出的均方误差E(k)。

(4)判断误差精度是否达到要求，若没达到，进行步骤(4)；否则，保存各项参数，算法结束。

(5)更新隐含层与输出层间的权值s′om、输入层与隐含层间的权值w′ro、输入层与隐含层间的阈值εo(k)、隐含层与输出层间的阈值ζm(k)。

(6)判断是否达到设置的最大网络训练次数M，若没达到，转回步骤(3)；否则，算法停止。

3 参数估计

系统参数辨识方法有多种，比如最小二乘法、遗忘因子最小二乘法、加权最小二乘法等。与这些方法相比，现使用含有遗忘因子和加权因子的折息递推辨识算法(recursive method with discounted measurements，RDM)辨识参数，它具有时变跟踪能力即动态特性，同时还能保持区间内系统数据的平均特性。

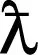
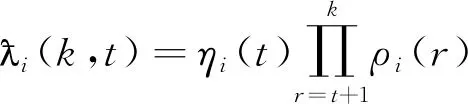
(22)

考虑最小二乘辨识模型[式(14)]，对第i个子系统选取准则函数为

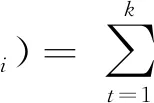
(23)

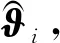
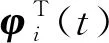
(24)

则可推导出k时刻第i个子系统参数估计值为

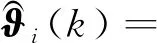
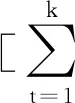
(25)

定义协方差矩阵ψi(k)为

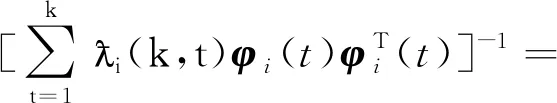
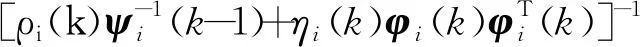
(26)

定义增益矩阵ћi(k)为

ћ(k)=ηi(k)ψi(k)φi(k)

(27)

由式(25)～式(27)推导，可得如下折息递推辨识算法：

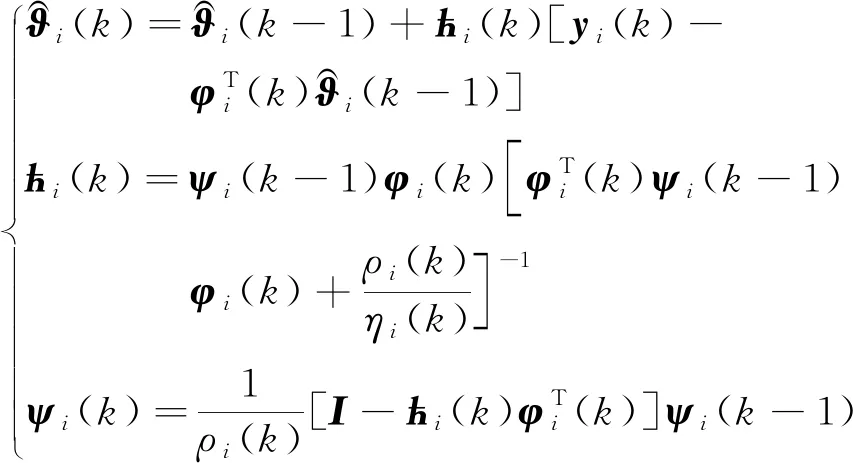
(28)

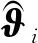
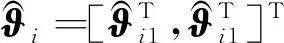
(29)

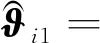
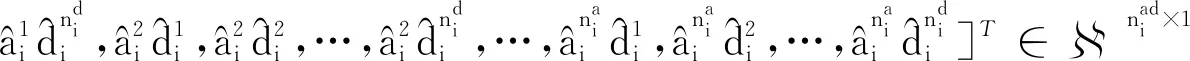
(30)

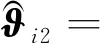
(31)

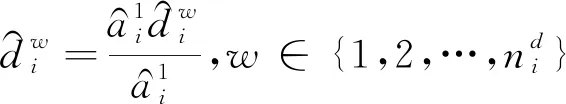
(32)

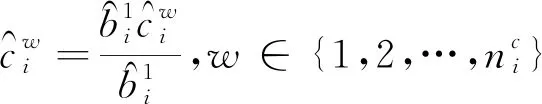
(33)

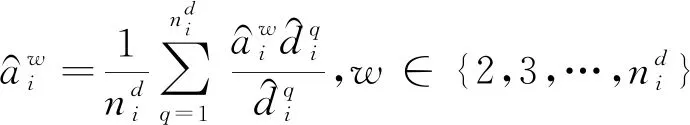
(34)

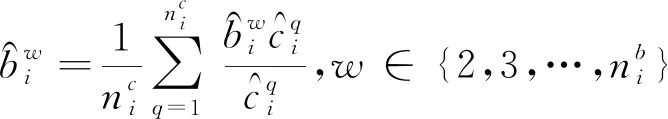
(35)

通过以上公式，对于第i个系统，在第k次迭代中，系统辨识参数结果为

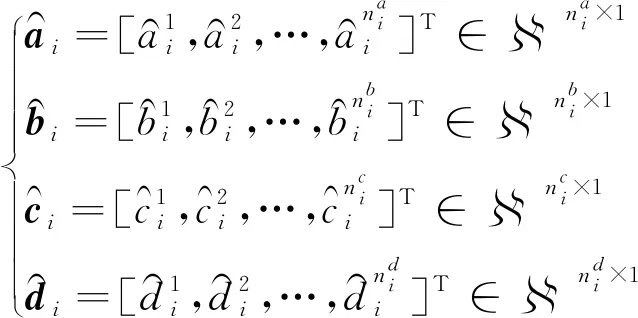
(36)

基于折息递推辨识算法的参数估计步骤如下：

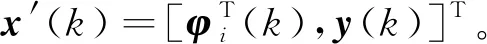
(3)由训练后的BP神经网络输出δ(k)，通过δ(k)预测当前子系统i。

(6)若k未达到最大值，则k=k+1，转到步骤(2)；否则，结束算法。

4 仿真

考虑如下由3个Hammerstein-Wiener非线性系统结构组成的切换非线性系统：

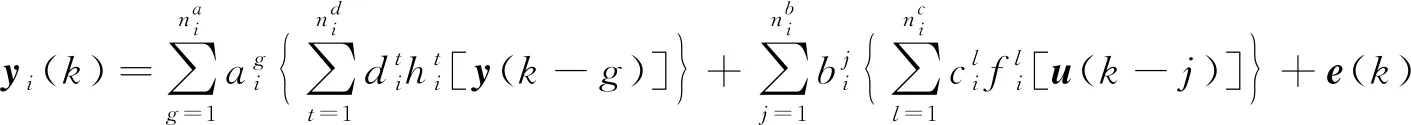
子系统1：

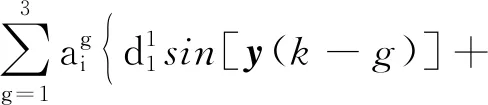
其中系统参数：a1=[1,-0.34,-0.5]T,b1=[1,-0.3,-0.2]T,c1=[0.26,-0.1,-0.96]T,d1=0.25,0.35,1.05]T。

子系统2：

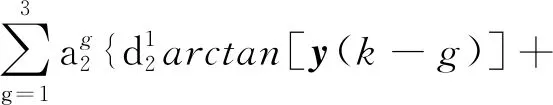
其中系统参数：a2=[1,-0.21,0.25]T,b2=[1,0.44,-0.9]T,c2=[0.78,0.12,0.61]T,d2=[0.51,-0.9,-0.12]T。

子系统3：

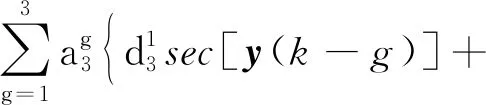
e(k)。

其中系统参数：a3=[1,0.53,0.75]T,b3=[1,-0.6,-0.2]T,c3=[0.14,0.42,-1.01]T,d3=[-0.6,0.8,0.41]T。

在仿真中，输入u(k)为零均值、单位方差的高斯白噪声序列，噪声信号e(k)为零均值、方差δ2为0.001的高斯白噪声序列，输入信号和输出信号的噪信比为SNR=0.13%。同时，加权因子取η1=η2=η3=0.999，遗忘因子取ρ1=ρ2=ρ3=0.999。

系统采用随机切换方式，每50个样本周期性等概率随机在子系统{1,2,3}中切换，产生10 000个已知切换规律的训练数据，经过神经网络训练建立神经网络预测模型。另外，在线对2 000个未知切换规律的测试数据进行切换规律预测。BP神经网络初始参数设置中，所有阈值、权值初始值为0，训练误差E′=10-10，学习率ζ=0.000 1，输入层、输出层神经元数目分别为19和3。由式(29)确定隐含层数目大致范围为[5,15]，为选取更合适的隐含层数目，将隐含层数目范围扩大至[4,70]，并取其中的偶数。在训练时，每个隐含层数目进行100次实验，统计训练时间及切换规律预测正确率，并观察正确率分布情况。不同隐含层数目正确率中位数和正确率均值变化图如图3所示，不同隐含层数目训练平均时间和正确率标准差变化图如图4所示。

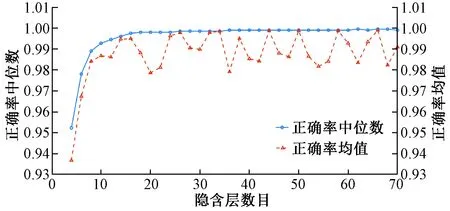
图3 不同隐含层数目正确率中位数和正确率均值变化图Fig.3 Variation plot of the median of the correct rate and the mean of the correct rate under different numbers of hidden layers

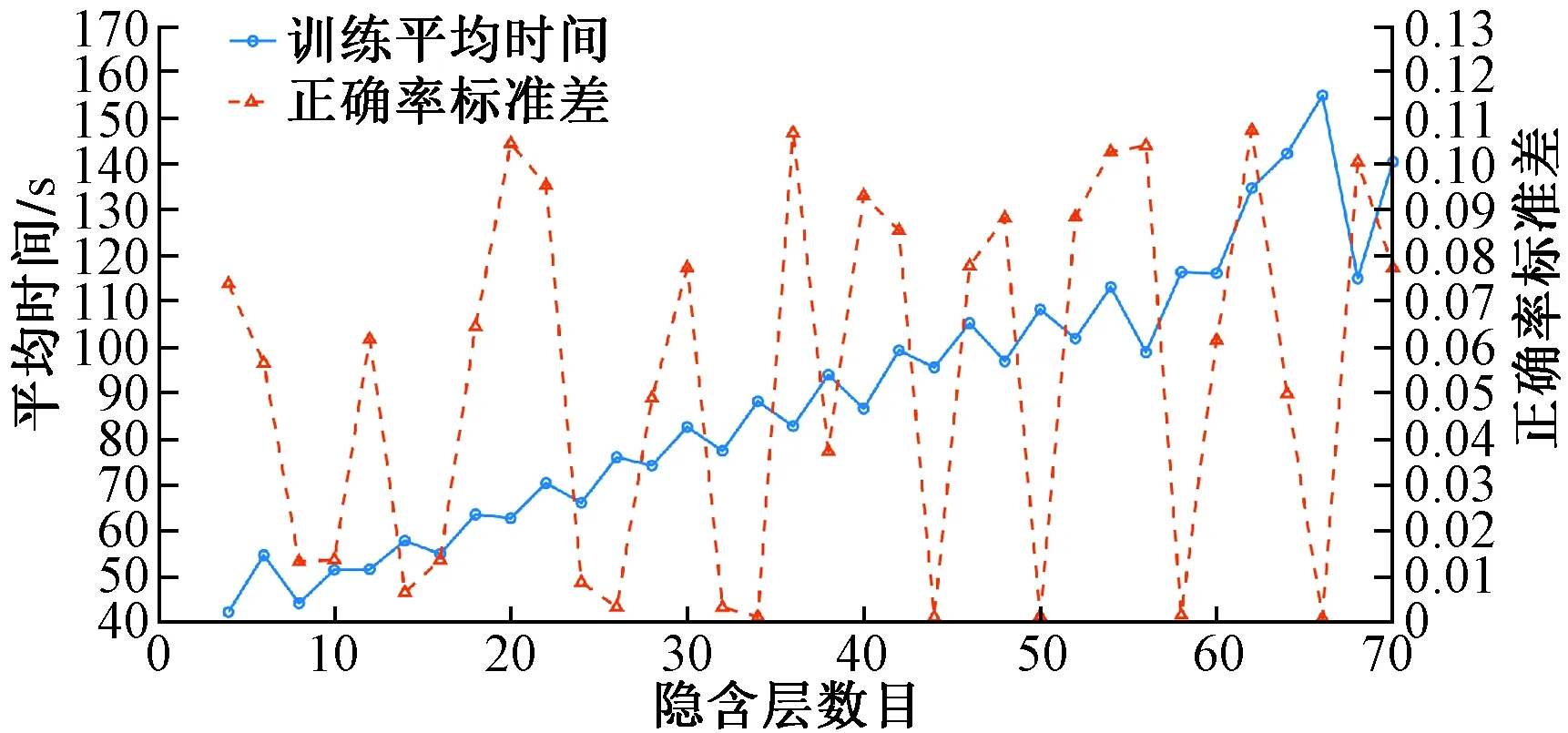
图4 不同隐含层数目训练平均时间和正确率标准差变化图Fig.4 Variation plot of the training average time and variation plot of the standard deviation of correct rate under different numbers of hidden layers

从图3、图4可看出，不同隐含层数目在100次实验中，隐含层数目为34时，切换规律预测正确率较高且波动较小，同时训练时间较为合适。通过对比可以看出，选取34作为隐含层数目，对切换非线性系统进行切换规律预测。切换非线性系统实际切换规律如图5所示，通过神经网络预测得到的切换规律如图6所示，预测得到的切换规律正确率为99.900%，两条曲线基本接近，可将预测规律近似为实际切换规律。在此基础上，通过100次重复实验，将本文方法与投影子空间法[14]、支持向量机(support vector machine，SVM)法进行对比，统计得到不同方法切换规律预测错误率的箱形图，如图7所示。从图7可以看出，本文方法分类错误率主要集中在0～4%，低于其他两种算法。

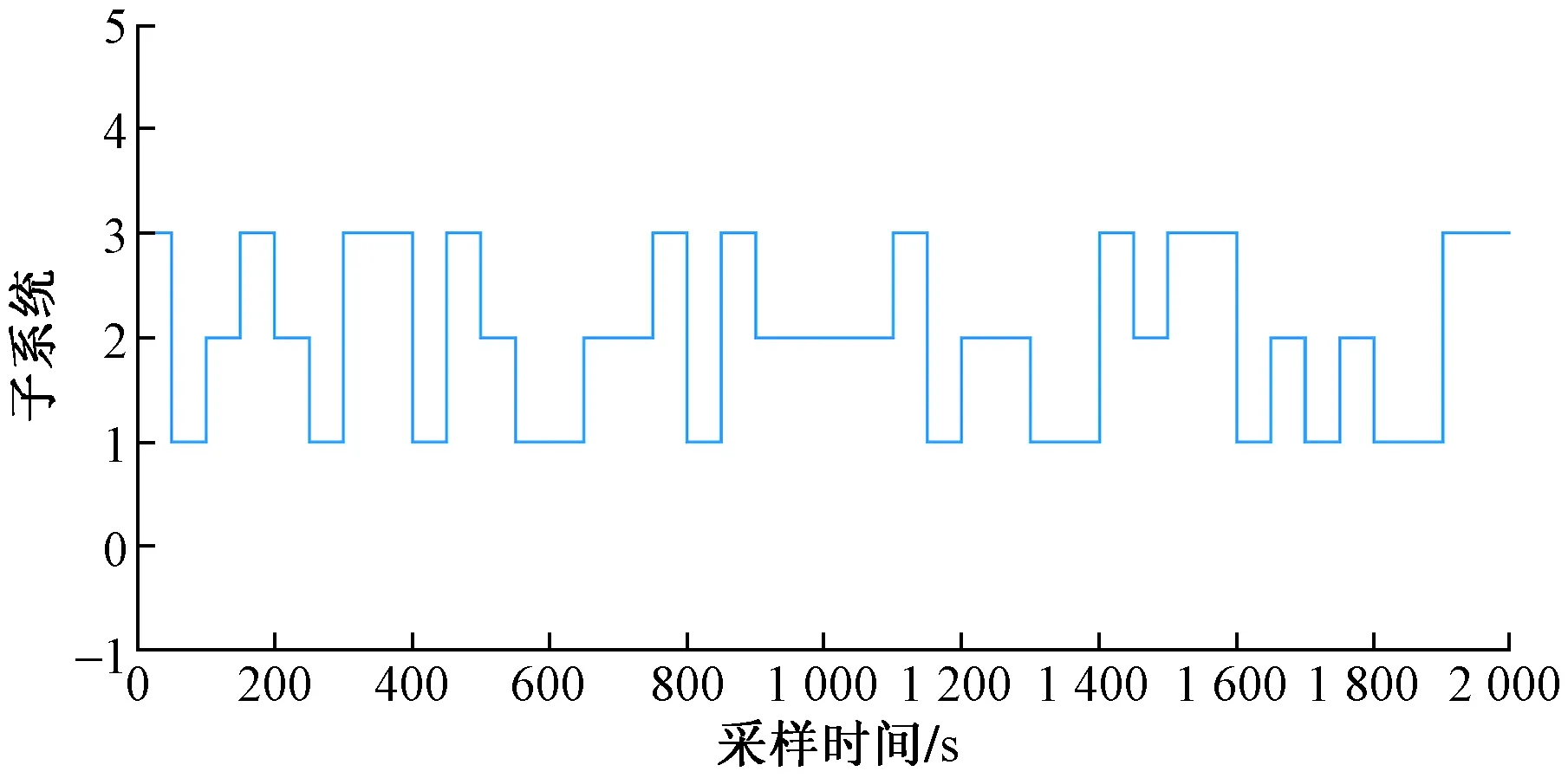
图5 切换非线性系统实际切换规律Fig.5 The actual switching rules of switching nonlinear systems

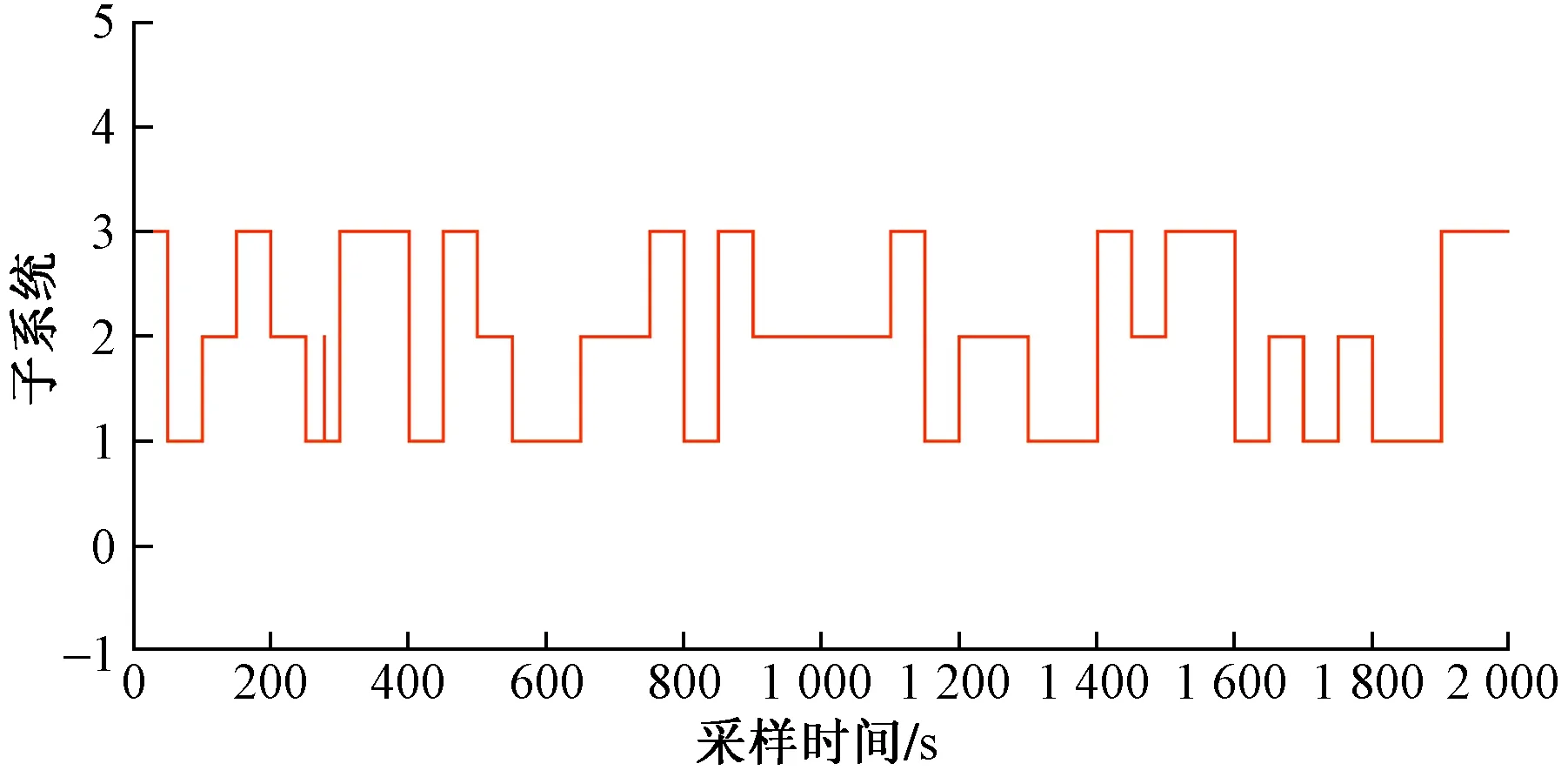
图6 系统切换规律的预测Fig.6 Prediction of system switching rules

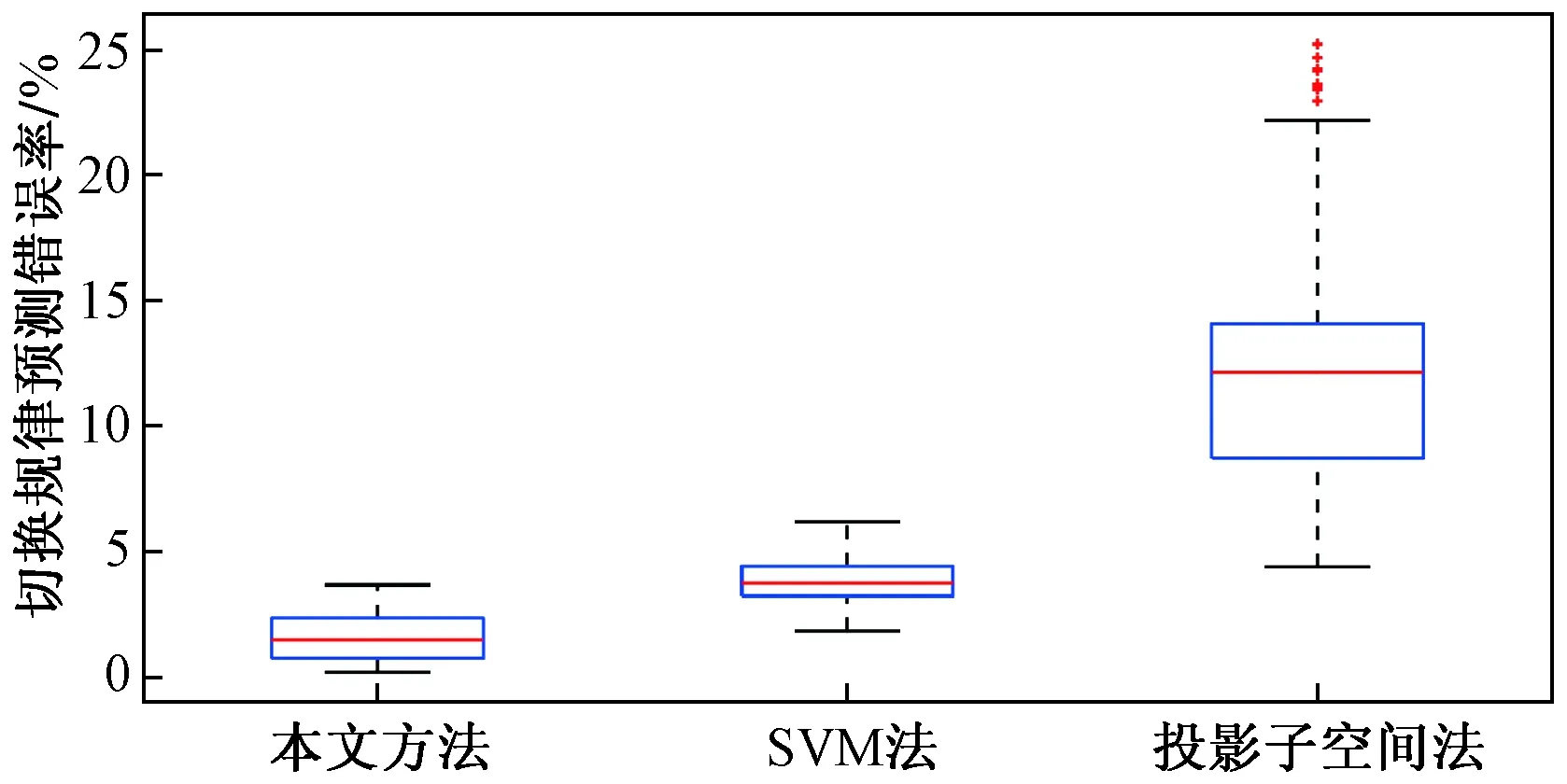
图7 不同方法切换规律预测错误率的箱形图Fig.7 Box plot of prediction error rate of switching rules under different methods

在上述预测模型基础上，不同算法辨识统计结果如表1所示，其中err为各个子系统参数辨识结果最终的总体相对误差。第一组为通过递推最小二乘算法(recursive least squares，RLS)获得的参数辨识结果，第二组为加权最小二乘算法(recursive weighted least squares，RWLS)获得的参数辨识结果，第三组为遗忘因子最小二乘算法(recursive forgetting factor，RFF)获得的参数辨识结果，第四组为折息递推辨识算法获得的参数辨识结果。四种方法参数辨识总体相对误差曲线如图8所示。

表1 不同辨识算法的统计结果

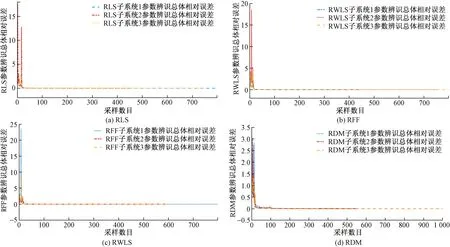
图8 RLS、RFF、RWLS、RDM参数辨识总体相对误差曲线Fig.8 RLS, RFF, RWLS and RDM parameter identification overall relative error curve

以上仿真结果表明：

(1)BP神经网络对于切换非线性系统具有良好的拟合性，神经网络经过训练后建立的预测模型，能够较为准确地在线预测出系统的切换规律。

(2)对于有噪声存在的切换非线性系统参数辨识，折息递推辨识算法具有的动态特性和平均特性，充分利用了系统数据信息，使参数辨识精度较高、效果更好。

5 结论

针对Hammerstein-Wiener切换非线性系统，提出了BP神经网络和折息递推辨识算法对Hammerstein-Wiener切换非线性系统的切换规律和参数进行辨识。仿真实验结果表明，通过训练后的BP神经网络能够较为准确地预测切换规律，结合折息递推辨识算法可以比较准确地辨识切换非线性系统参数。对于切换规律未知的切换非线性系统辨识还是比较困难的，它将是今后这类系统辨识研究的重点，研究者将进一步探索。