一种针对金属刀具的毫米波回波信号分析方法

2021-05-06裴一峰陈国平黄超意

科学技术与工程 2021年5期

裴一峰，陈国平，黄超意，管春

(重庆邮电大学光电工程学院，重庆 400065)

近年来，随着世界各地的恐怖分子在公共场所中行动愈加猖獗，为保障人们的出行安全，基于成像技术的安检系统应运而生[1]。然而，传统的成像安检系统通常需要先对人体进行全面扫描以获取相关数据后，再将采集得到的数据进行成像，以观察的方式辨别被检查人员是否携带危险金属物品。该技术扫描时穿透力弱，具有弱电离性以及需要专业人员对成像图中的目标物进行一一辨认导致实施效率低等问题[2]。因此，如何有效地对机场、车站等公共场所中的大量出行人员进行安全检查，以避免危险金属物品进入公共场所愈加受到研究人员的关注。

为解决传统的成像安检系统中存在的弱电离性、分辨率低等问题，毫米波因其能穿透衣物但不穿透人体的特点，从而能够用于对人体随身隐匿物品进行探测并成像。此外，毫米波不具有电离性，相比于X射线，基于毫米波的成像技术对人体无辐射伤害，故能够保障人体健康[3]。因此，毫米波成像技术逐渐成为人体安检领域的重要研究方向。

目前，Millvision、TRW等公司已经成功研制出被动式毫米波安检系统，但是该系统重构一幅毫米波成像图需要30 min，耗时太长，不能较好满足安检需求。随着对毫米波成像技术的深入研究，主动式毫米波安检系统也相继问世[4]。主动式相比较于被动式，灵敏度较高，耗时缩短，但是存在成像精度不够高等问题。基于此，中外大多数学者更倾向于研究主动式毫米波成像技术，并且从提高成像精度的角度对主动式成像技术进行优化，使得成像时间开销进一步递增。文献[3]提出了一种精确极大似然(exact maximum likelihood)算法，通过直接转换坐标系并加入随机噪声来建立模型。此方法提高了成像精度，付出的代价是消耗较长时间。文献[4]对精确极大似然算法进行了修正，加入转换误差进行改进，相对来说提高成像精度，但是仍然存在耗时长等问题。

此外，由于安检系统需要对每个被检测人员进行一个耗时较长的成像操作，因此当机场、车站等公共场所客流量增加时，成像系统对时间的消耗大大增加了安检任务压力，安检效果远低于预期水平。因此，利用毫米波技术实现精确成像的安检系统会增加人员通过安检的时间，存在缺乏快速性、效率低和耗时长等问题。

为权衡精确成像时间开销大与准确检查金属刀具等危险物品之间的矛盾，现提出一种应用在毫米波安检领域的基于矢量峰值法的毫米波回波信号分析方法。该方法通过直接对毫米波回波信号的特征进行分析处理，以便将具有金属刀具特征的回波信号筛选出来。一方面，若回波信号中不具备金属刀具的特征，则可避免不必要的精确成像，可缩短安检的整体时间花销，以满足大规模客流量的安检需求。另一方面，若是回波信号含有金属刀具的特征，则再将此回波信号进行高精度成像处理，以绘制完整的危险品图像，使得成像过程更具有针对性。

1 回波信号分析方法的构造与实现

1.1 小波变换理论

通常情况下，处理与分析信号一般采用傅里叶变换。但是，由于傅里叶变换的窗口不会随着频率变化而改变，导致采用傅里叶变换处理信号时，难以分离出在不同频率中的有用信号[5-8]。依据小波变换的“时间-频率”窗口能够动态调整的特点，从而达到在不同频率中获取有用信号的目的[9]。具体地，小波变换“时间-频率”窗口示意图如图1所示。

a为尺度；为平移量；b为时间点图1 时间-频率窗口示意图Fig.1 Schematic diagram of time-frequency window

此外，采用傅里叶变换处理实测数据的杂糅随机变化噪声，会造成在去除噪声的同时也平滑了信号瞬态分量的问题，而这些瞬态分量包含一部分所需信号，因此难以将信号的高频部分与噪声分离开来。相比于采用传统的傅里叶变换，小波变换具有良好的局部特征，能够较好地提取信号中的瞬态高频分量。故综合考虑，选择小波变换对回波信号进行分析。

设f(t)为毫米波回波信号，Fψ为回波信号f(t)的傅里叶变换形式，则

(1)

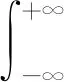
式(1)中：i为虚数。若核函数ψ(t)满足容许性条件：

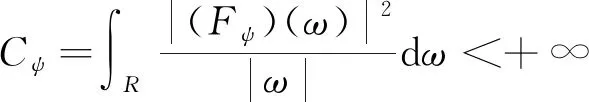
(2)

式(2)中：R为定义域。同时，称该函数ψ(t)为基小波。

原始回波信号f(t)∈L2(R)的连续小波变换可定义为

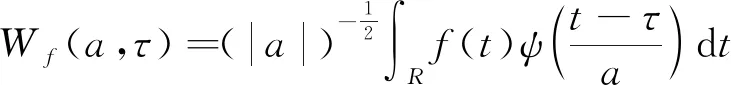
(3)

式(3)中：τ为平移量。

简单来说，原始信号f(t)进行小波分解时，f(t)被分解成低频信号a(t)以及高频信号d(t)，如图2所示。

图2 小波分解示意图Fig.2 Schematic diagram of wavelet decomposition

当f(t)中包含较多频率成分时，通常一次分解难以对数据进行分析，故需要对掺杂较多频率成分的低频信号进行再次分解[10]。其中，第二层分解则是在第一层的基础上将低频信号再分解为低频和高频两部分，余下部分以此类推。具体地，小波分解结构展示如图3所示。

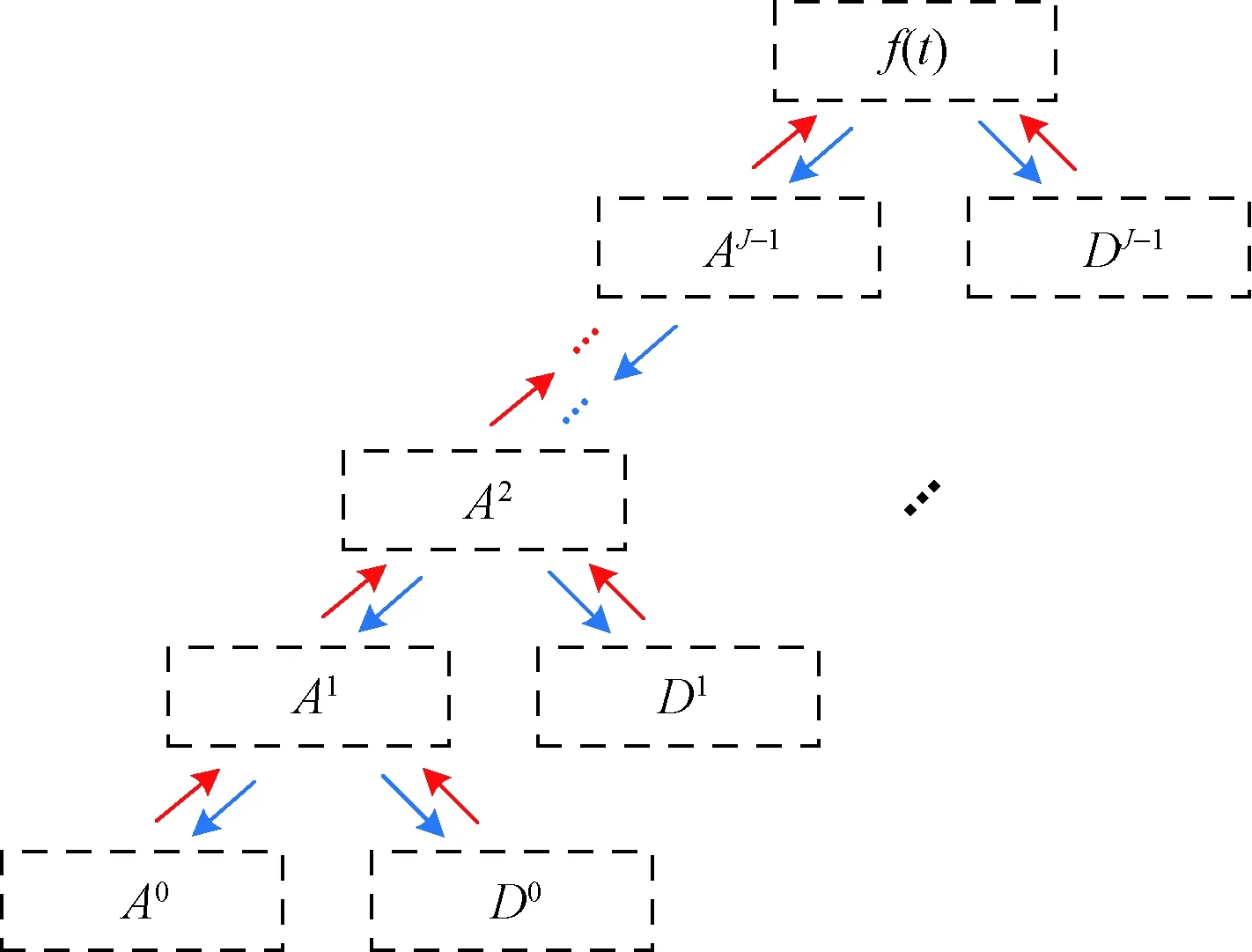
图3 小波分解树状示意图Fig.3 Wavelet decomposition tree diagram

因此，信号f(t)可表示为

f(t)=D(0)+D(1)+…+D(J-1)+A(0)

(4)

式(4)中：D为高频分量；J-1为对应的高频分量的层数；A为低频分量。

然而，在小波变换中，使用不同的小波基对同一信号进行匹配时，映射方式不同，导致利用不同小波基处理的同一信号结果之间存在差异性[11]。因此，小波基的有效选择对精确分离有用信号来说，显得尤为重要。对于小波基的选择，各领域学者皆有不同意见与想法，很难统一起来[12]。

在信号为毫米波回波实测数据的前提下，依托多次重复的实验数据，利用3种不同小波基对实验数据进行分析，得到的对比结果如表1所示。

表1 不同小波基对比表

如表1所示，Deubecheis和Haar小波基与实验数据波形契合度较低，且Deubecheis和Haar小波基处理实验数据后得到的峰值不易观察，即实验观察结果较差。Symlet小波基与实验数据波形较好地契合，且使用Symlet小波基处理实验数据后得到的峰值极易观察，实验观察结果较好。统筹考虑，最终选择了Symlet小波基，能够较好地分析毫米波回波信号。

1.2 矢量峰值分析方法的设计与实现

为了较好地获取原始回波信号中的金属刀具特征，提出一种应用在毫米波安检领域的针对回波信号的矢量峰值分析方法。包括信号模值提取、信号分解与重构以及矢量峰值分析三个阶段。

1.2.1 信号模值提取阶段

首先，设f=[A1,A2,…,A8]T表示毫米波原始回波信号，它是一个8×256矩阵。其中，矩阵f中的元素Ai(1≤i≤8)是利用毫米波装置经过一次完整的数据采集得到。也就是说，矩阵f包含8组独立的回波数据，具体表示为

[A1,A2,A3,…,A8]T

(5)

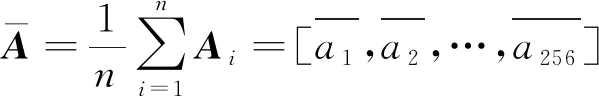
(6)

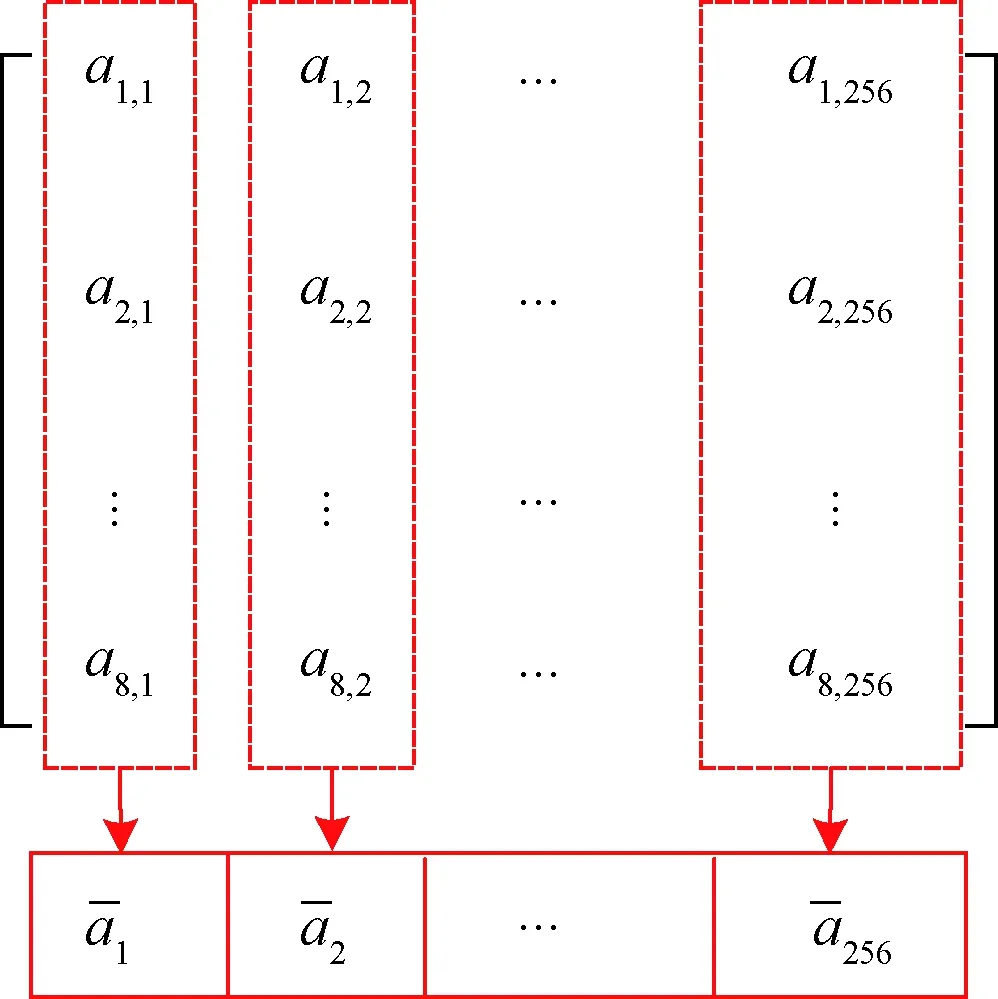
图4 矩阵均值计算示意图Fig.4 Schematic diagram of matrix mean calculation

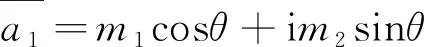
(7)

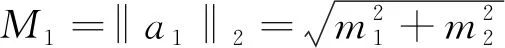
(8)

(9)

1.2.2 信号分解与重构阶段

1.2.3 矢量峰值分析阶段

首先，针对单独人体的情况，人体在频率处于610.5～1 221 kHz的总体表征为多反射目标。当小波变换对毫米波回波信号进行分解时，在对应频段分解层上的波形会呈现出多正峰值的特征。其次，针对仅有金属刀具的情况，由于金属刀具在相同频段上的总体表征为单反射目标。因此，它的反射信号在对应频段分解层上的波形会呈现出单正峰值的特征。最后，针对人体携刀的情况，处于相同频段时，人体的反射强度远远小于金属刀具的反射强度，故人体带刀的总体反射信号在对应频段分解层上会呈现出单正峰值的特征，即只有唯一正峰值。

综上，电磁波频率处于610.5～1 221 kHz，单独人体、仅有金属刀具、人体携刀三种情况的总体表征特点如表2所示。

表2 三种情况总体表征对比表

根据表2中仅有人、仅有刀、人携刀3种情况对比结果易知，根据信号的表征特点，能够较好地区分被检测人员是否携带金属刀具。其中，若是表征为单正峰值，则表示检测信号中包含金属刀具特征，从而反馈被检查人员携带有金属刀具。若表征为多峰值，则表明被检测人员未携带金属刀具。

综上，为清晰描述信号模值提取、信号分解与重构和矢量峰值分析三个阶段之间的关系以及如何对毫米波回波信号进行金属刀具的特征进行识别，绘制该分析方法整体框架图，如图5所示。

图5 毫米波回波信号分析方法整体框架图Fig.5 The overall frame of millimeter wave echo signal analysis method

2 实验仿真与分析

通过制订一种应用在毫米波安检领域的基于矢量峰值法的回波信号分析方法，能够鉴别出原始信号中含有的金属刀具特征，并利用呈现波形的峰值数量来检测是否携带金属刀具。通过实验仿真，将对上述方法在实测数据中进行正确性验证。

2.1 实验前期准备

首先，利用毫米波发射-接收装置获得人携刀和人无刀的实验数据。其次，使用MATLAB对上述两组数据分别进行处理，得到两组波形图，如图6所示。

图6 人携刀与人无刀对比图Fig.6 Comparison of people carrying knives and people without knives

由图6可知，无论是人携刀还是人无刀，两者之间的特征无明显差别。这是因为当信号中掺杂各种高低频率时，由于低频信号能量值较大，该混杂高低频信号分量的回波信号总体上表现为低频信号的特征。当混杂信号在低频时，人体的反射信号能量远大于刀具的反射信号能量。因此，无论是人携刀还是人无刀，原始回波信号波形总体上反映的皆为人体的低频信号特征，导致难以直接从实测数据中有效提取表征金属刀具的特征。

此外，考虑到高频信号具有剧烈震荡且迅速等特点，能够发现信号的更多细节信息，有利于找出金属刀具的特征。因此，需要将原始信号进行分离以获得实测数据含有的高频分量。

使用小波变换将原始回波信号进行分解并重构得到对应于频段610.5～1 221 kHz的高频分量。根据毫米波设备的采样率4.884 MHz和7分解层数计算可知，第二高频分解层对应此频段，也就是d2层。因此，对人体进行扫描采集数据之后，当回波信号在d2层被检测出正峰值数量为1时，可判定为人体携刀；当正峰值数量大于1时，可判定为人体无刀。在处理数据时，重点利用d2层，通过d2层正峰值的数量进行判定，实现检测出危险金属刀具的目的。

为排除人体形体差异，接下来将通过对照组与实验组来证明矢量峰值法的正确性，以保证实验的严谨性与科学性。

2.2 对照组实验仿真和结果分析

2.2.1 单独金属刀具实验

金属刀具实验场景的示意图如图7所示。

将金属刀具正对放置在毫米波发射装置前面，它们之间的距离为1.5 m。根据毫米波装置采集得到回波信号，再利用MATLAB程序实现得到的d2层波形如图8所示。

图7 金属刀具实验场景图Fig.7 Experimental scene of metal knife

图8 金属刀具d2层分解叠加图Fig.8 Metal tool d2 layer decomposition overlay

由图8可知，金属刀具的毫米波回波信号利用小波变换分解重构后，在d2层的正幅度维上表现为单峰值的特征。重复25组上述实验皆可得到类似具有单峰值特征的波形结果。因此，根据金属刀具实验的结果，足以说明金属刀具的毫米波回波信号在d2层表现为单峰值特征。

为准确获取表征单独人体利用毫米波装置反射的回波信号，并验证频率在610.5～1 221 kHz的d2层上呈现多峰值的特征的正确性。采用金属圆柱体代替人体的方法，排除人体形体差异，以验证人体为多峰值特征。下文将利用金属柱实验对人体的多峰值特征进行正确性验证。

2.2.2 金属柱实验

金属柱实验场景示意图如图9所示。

除了将金属刀具替换成金属圆柱体(π×0.05 m2×0.15 m)，金属柱实验条件与单独金属刀具实验其他条件均保持一致。根据毫米波装置采集得到回波信号，再利用MATLAB程序实现得到的d2层波形如图10所示。

图9 圆柱体实验场景图Fig.9 Cylinder experiment scene graph

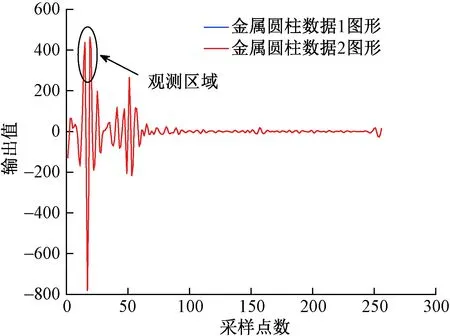
图10 金属柱体d2层分解叠加图Fig.10 Metal cylinder d2 layer decomposition overlay

由图10可知，分解-重构金属圆柱体的回波信号后，在d2层的正幅度维上表现为多峰值的特征。为了排除实验的偶然性，经过重复25组上述实验，皆可得到与图10类似具有多峰值特征的波形结果。总之，在排除人体形体差异情况下，人体的毫米波回波信号在d2层表现为多峰值特征。

综上，单独金属刀具实验证明了当毫米波频率处于610.5～1 221 kHz时，金属刀具为单反射目标，它的反射信号在d2层上呈现出单正峰值特征。金属柱实验证明了当处于相同毫米波频段时，人体为多反射目标，毫米波反射信号在d2层上呈现出多峰值特征。

然而，当金属圆柱体表面粗糙坑洼破损且不平滑时，金属圆柱体表面可能会形成较多的局部金属平面。因此，当毫米波信号发射到此金属圆柱体时，较多的局部金属平面反射信号强度会大于金属圆柱体的其他散射信号，因此最终毫米波装置接收的反射信号可能会呈现出类似单反射目标的特征。金属柱实验是为了排除人体形体差异，同时模拟人体的多反射特征，因此在选择金属圆柱体进行实验时，需选择表面光滑且无坑洼破损的金属柱，防止金属柱表面出现较多局部平面干扰实验结果。

2.3 实验组仿真和结果分析

2.3.1 人体无携刀实验

人体无携刀实验示意图如图11所示。

根据毫米波装置采集得到回波信号，再利用MATLAB程序实现得到的d2层波形如图12和图13所示。

图11 人无刀实验场景图Fig.11 Human without knife experiment scene

图12 人无刀d2层分解叠加图Fig.12 Man without knife d2 layer decomposition overlay

图13 人无刀d2层分解峰值处放大图Fig.13 Enlarged view of the decomposition peak of d2 layer without knife

由图12和图13可知，人体未携金属刀具的回波信号在d2层的正幅度维上表现为多峰值的特征。为了排除实验的偶然性，经过重复25组上述实验，皆可得到与图12类似具有多峰值特征的波形结果，进而说明利用矢量峰值法能够对人体无携刀情况进行鉴别。

2.3.2 人体携刀实验

人体携刀实验场景示意图如图14所示。

图14 人携刀实验场景图Fig.14 Experimental scene of a man carrying a knife

根据毫米波装置采集得到回波信号，再利用MATLAB程序实现得到的d2层波形如图15所示。

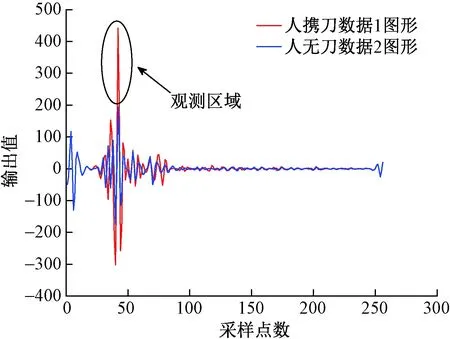
图15 人携刀d2层分解叠加图Fig.15 Man carrying knife d2 layer decomposition overlay

由图15可知，将人体携金属刀具的毫米波回波信号在d2层的正值幅度维上，可以明显地呈现出单峰值的特征。为了排除实验的偶然性，经过重复25组上述实验，结果皆为单峰值特征。

从人体无携刀实验和人体携刀实验结果来看，当人体未携金属刀具时，在d2层上表现为多峰值特征；当人体携金属刀具时，在d2层上呈现为单峰值特征。因此，当进行安检时，在毫米波安检设备获取到原始回波信号后，将原始回波信号进行分解重构，若在d2层呈现为多峰值特征，则判定人体未携金属刀具；若在d2层呈现为单峰值特征，则判定人体携金属刀具。

若人体携带的金属刀具配置皮革刀套或者塑料刀套等保护装置时，毫米波能够穿透这些保护装置从而对金属刀具进行探测。保护装置可能会吸收或者散射一小部分信号，但是金属刀具的反射信号能量远大于保护装置的散射信号能量，最终反射信号总体还是表现为单峰值特征，只不过最终反射信号的能量会有所下降。

2.4 性能分析

在2.2节和2.3节中，通过利用对照组与实验组的仿真实验结果，有效地证明了本文方法的正确性。接下来，针对矢量峰值分析方法的性能与类似方案实验进行对比，结果如表3所示。

可辨别率指当处理结果被呈现在安检人员面前时，若为成像图片时，该图片包含各种物体的信息，此信息多而杂乱，安检人员难以立即判断出此图片中是否含有危险物品，可辨别率很低。然而，本文方法可以直接根据d2层的峰值个数，从而立刻确定是否携带危险金属刀具，可辨别率高，几乎可以说达到100%，相对而言提高了安检效率，减轻了安检人员负担。

表3 类似方案对比表

由表3可知，与文献[1，5，10]相比，本文方法在检测波形图的判定结果为无金属刀具时，无需进行成像操作。与类似方案相比，本文方法进行检测所需时间仅为0.2 s(±0.05)，相比于文献[1]提高了24倍，相比于文献[5]提高了149倍，相比于文献[10]提高了299倍。这极大地减少了无金属刀具数据的成像时间，有效地提高了安检效率。