基于改进灰狼算法优化自适应相似日选取的小水电短期预测

2021-05-06王凌云王舟盼

科学技术与工程 2021年5期

王凌云，王舟盼，安晓，赵魏

(1.三峡大学电气与新能源学院，宜昌 443002； 2.国网湖北送变电工程有限公司，武汉 430061)

近年来，作为清洁能源的小水电变得越来越受各地区重视，随着其装机容量越来越大，对地方电网的影响也逐年增大[1]。然而大部分小水电站都是径流式，调节能力差，且极易受到天气变化的影响，使得小水电机组出力难以准确预测，从而影响到地区网供负荷的供给。因此，为了增强电网对小水电的调度能力，准确预测小水电发电负荷成为至关重要的问题[2]。

目前，中外关于径流式小水电站出力预测的研究不多。根据文献[3]所述，如何有效地选取相似日是提高负荷预测精度的主要方向之一。文献[4]提出用标幺曲线和基值来预测小水电负荷，并在选取相似日时采用二次筛选的方法。文献[5]在求取相似日时分别计算各影响因素的相似度，最后将所得的相似度全部相乘得到一个综合相似度。文献[6]提出一种基于新欧几里得范数的带权因子的相似日方法，将各影响因子相似度以平方求和的方式求取出综合相似度。为更深入研究小水电的出力规律，并以此来改善相似日选取方法，现提出以中国阴历的方式来划分负荷和气象数据，且在研究中发现影响因子对小水电出力的影响程度并不是一成不变的，故为了体现实时性，为每个影响因子赋予一个单独的权重，并提出采用智能算法对各个权重进行优化，灰狼算法作为一种模仿狼群捕猎的智能算法，相比于其他算法具有收敛速度快、模型简单的优势[7-8]，因此，采用灰狼算法来优化各权重。

文献[9]指出任何单一预测方法都有其局限性，如何建立组合预测模型已经成为负荷预测的研究热点。文献[10]提出一种基于多目标优化算法的组合模型，实验结果证明组合模型的准确性和稳定性均优于单一模型。文献[11]指出线性组合预测模型仍然存在改善的可能性，并提出基于广义回归神经网络(general regression neural network，GRNN)的非线性组合预测方法，实验数据表明非线性组合预测模型的预测精度更高。

现提出一种基于改进灰狼算法优化GRNN的非线性组合预测模型，采用改进灰狼算法对 GRNN网络参数进行优化，并利用优化后的GRNN模型对反向传播(back propagation,BP)神经网络和径向基函数(radial basis function, RBF)神经网络这两种网络模型的输出值进行非线性组合预测。

1 小水电相似日选取

1.1 基于阴历划分的小水电出力分析

预测小水电的出力不同于全社会用电负荷，全社会用电具有很明显的周周期性规律[12]，并且有工作日和休息日的区别，休息日的负荷一般会低于工作日的负荷。而小水电负荷与社会生产、生活联系不强，其出力主要受气象因素影响。故本文不以传统的年、月采集负荷数据，在研究小水电出力时按阴历的周期划分小水电负荷，根据中国二十四节气特点，提出选用节气负荷来采集数据的思路。采用阴历来划分负荷数据更适用于分析小水电的规律性，并且能够有效缩短数据的采集间隔周期，更能清楚地反映小水电负荷随着时间、气候变化而变化的规律性，克服了传统以跨度较大的年月来采集负荷数据导致数据对影响因素变化反应不灵敏的缺点。将小水电负荷数据以节气的周期进行划分，二十四节气按1～24序号排序，如图1所示。

由图1可以看出，曲线的高峰及低谷所在时间段具有一定的相似性。根据阴历节气划分数据可以在一定程度上体现枯水季和丰水季。随着第一个节气立春的到来，表示着正逐步进入丰水期，小水电出力开始缓慢增加。直至第13个节气立秋的到来，小水电出力开始缓慢减少，时间进入枯水期。丰水期和枯水期对小水电出力的影响不同，由于不同季节降雨汇流的过程可能存在差异，所以不同汛期降雨对小水电出力的影响也不相同，其中丰水期降雨影响更加明显。

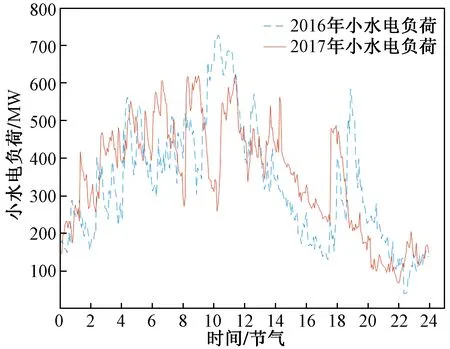
图1 小水电节气负荷Fig.1 Solar term load of small hydropower

1.2 基于自适应的相似日选取

相似日选取方法是采用差异评价函数，找出若干条与待测日曲线最相似的历史日曲线。文献[13]通过分析特征曲线的形状和距离，采用改进的灰色关联分析法来计算预测日和历史日的关联度，最终以加权平均的方式来选取相似日。在选取相似日时综合考虑气象、时间和节气因素，但是三种因素对小水电出力影响并不是一成不变的，例如在丰枯期的降雨量对小水电出力影响悬殊[14]。因此，提出一种自适应的相似日选取方法，在计算最终相似度时，没有采用加权平均的方法，而是赋予影响因素各自的权重，利用改进的算法对权重进行优化得到一个综合相似度σj，计算式可以表示为

σj=c1γj+c2Γj+c3η(j)

(1)

式(1)中：γj为在气象因素上待测日和历史日的相似度；Гj为待测日与历史日在时间上的相似度；η(j)为节气上的相似程度；c1、c2和c3分别为权重系数。

1.3 气象因子

1.3.1 计及滞后和累积效应的等效降雨量计算

现小水电大多分布于山区且大部分都是径流式水电站，调节能力较差，所以降雨量的大小成为影响小水电出力的主要因素，而降雨量有一定的滞后和累积效应，实时测得的降雨量并不是真正影响小水电出力的值，故需计算出真正影响小水电的等效降雨量。降雨在地面汇集并影响小水电出力的过程需要一个较长的时间。因此，降雨量影响小水电机组发电存在一个明显的时间滞后性。小水电发电的累积效应主要表现为：当持续大量降雨过程停止后，小水电机组发电仍会持续增加一段时间，累积和滞后性体现了小水电出力对降雨量感知具有“惯性”。

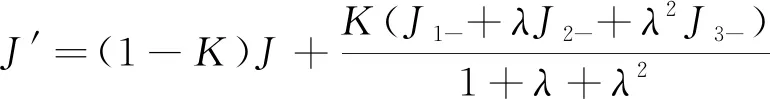
(2)

式(2)中：K为累积系数；λ为衰减系数，即每往前推1 d，权重系数衰减的比率；Ji-为需要等效的前i天的降雨量；J为需要等效的降雨量；J′为等效后的降雨量。

1.3.2 气象因素特征向量的相似度计算

对小水电发电影响最大的是温度和降雨量，选取的气象因素分别为最高温度、最低温度、平均温度和降雨量，若设待测日的气象特征向量为x，则预测日前第j天的气象特征向量为xj，4个影响因素构成的向量为xj=[xj(1)，xj(2)，xj(3)，xj(4)]。待测日的气象特征向量x与预测日前第j天的气象特征向量xj的关联系数ξj为

ξj(k)=

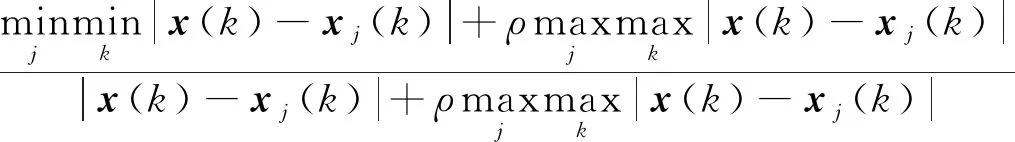
(3)

每个气象因素特征分量都会计算出各自的关联系数，不便于比较，根据式(4)可得第j个历史日的气象因素特征向量xj(k)与待测日x(k)的关联度γj,即

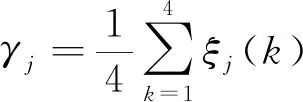
(4)

1.4 时间因子

时间因子表示预测日与历史日在时间上的相似程度，包括汛期相似程度和日期相似程度。汛期相似程度用以判断二者是否同处丰水期或枯水期，而日期相似程度指历史日与待测日的相隔天数，在数值上表现为“近大远小”。

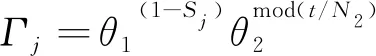
(5)

(6)

式中：t为预测日与第j个历史日相隔的天数；mod为取余函数；θ1=0.93为历史日与预测日是否所处同一个丰水期或者枯水期的衰减系数；θ2=0.95为预测日和历史日相隔每增加1 d的日衰减系数；N2取值为360。

1.5 节气因子

节气在一定程度上可以反映季节、气候的变化规律。处在同一节气的气象具有一定的相似性，故引入节气因子判断二者是否处于同一个节气。

η(j)=β(1-Sj)

(7)

(8)

式中：β为衰减系数，一般取值为0.98；Sj为一个标记变量。

2 预测模型与实现流程

2.1 广义回归神经网络

广义回归神经网络是一种建立在数理统计基础上的径向基函数网络，在非线性建模、学习速度和分类能力方面具有较强优势[15]，其不仅可以解决非线性组合问题，还可构建动态学习模式并作出预测。其结构如图2所示。

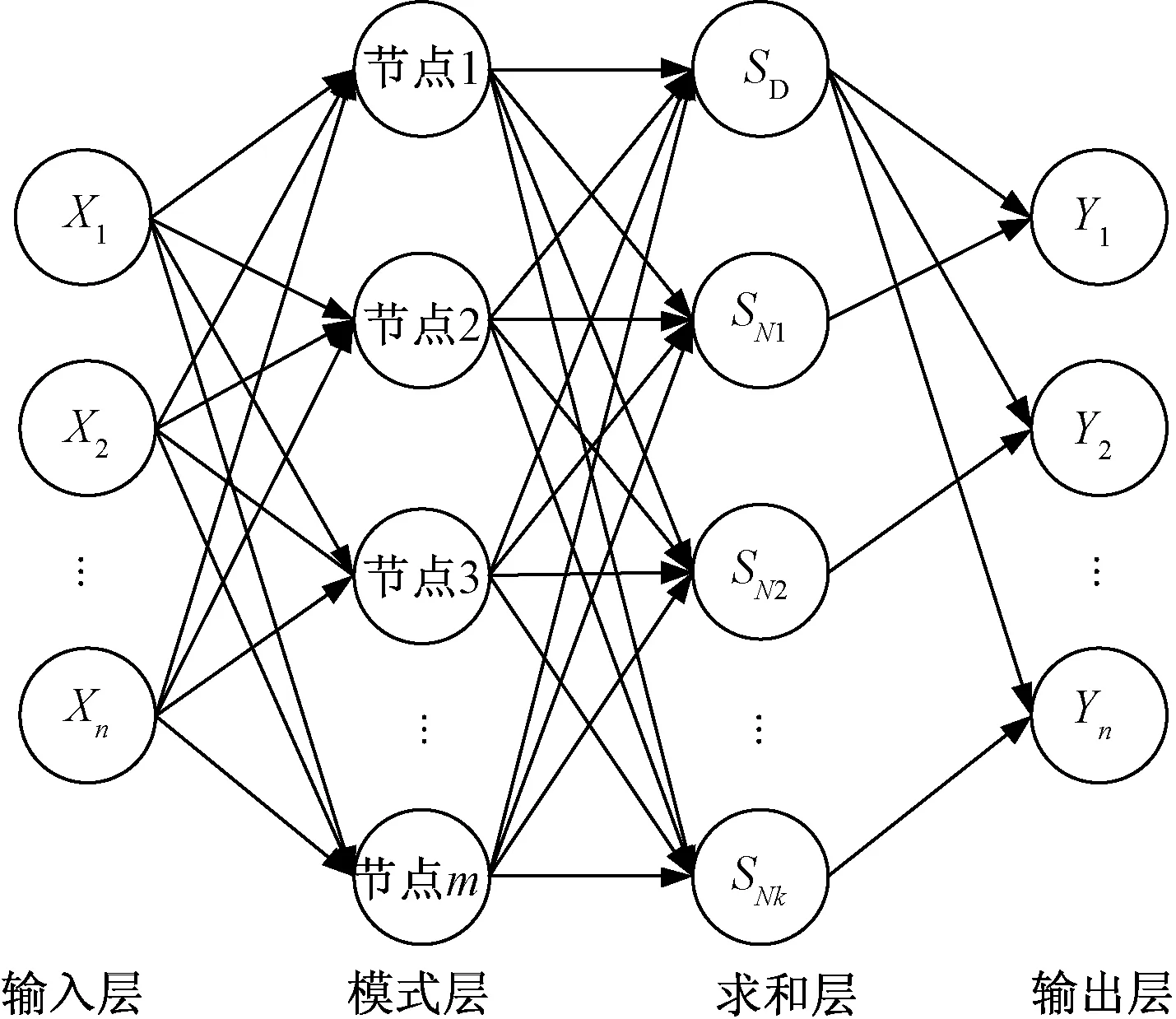
图2 广义回归网络结构Fig.2 Structure of generalized regression networks

输入层：n维输入变量X=[X1,X2,…,Xn]T。

模式层：模式层神经元的传递函数为

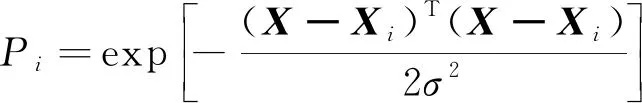
(9)

式(9)中：X为网络的输入变量；Xi为第i个神经元对应的学习样本(i=1, 2,…,n)；σ为平滑参数；

求和层：在该层主要进行两部分的求和过程。第一个部分为对模式层输出加权，假设模式层输出变量为{g1,g2,…,gm}，则求和层第一部分为

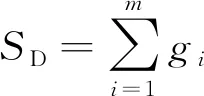
(10)

其余k个神经元输出为模式层输出的加权之和为

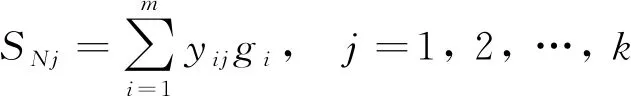
(11)

式(11)中：yij为第i个模式层神经元对应样本的第j个系数。

输出层：第j个输出层神经元的输出量为求和层第二部分输出值SNj与第一部分输出值的比值。

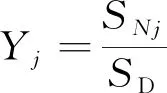
(12)

2.2 基于优化GRNN的非线性组合预测

非线性组合预测是时间序列趋势预测的重要发展方向[16]，GRNN作为非线性回归分析的一种网络，擅长求解非线性组合问题。文献[17]在建立预测模型时，分别将三种单一预测模型结果作为GRNN的输入量，最后利用算法集成多个GRNN输出得到最终预测值，实验表明，所提非线性组合模型预测精度均高于各单一预测模型。故在建立小水电预测模型时，利用单一的 BP和 RBF神经网络分别进行预测得到两组预测值，然后将两组神经网络预测值作为 GRNN的输入量，最后采用 GRNN进行非线性组合预测得到最终的小水电预测值。但是GRNN网络的预测效果与其本身的平滑因数有着很大的关联，若平滑因数取值过大时，GRNN的输出值越接近所有样本的平均值。反之，若平滑因数的值趋向于0，它的预测值只会非常接近训练样本，一旦需要预测的值没有被包含在训练集内，预测精度有可能会非常低。故平滑因数σ需要被优化，以此使预测效果达到最佳。

2.3 改进灰狼算法

虽然常规灰狼算法(grey wolf optimizer，GWO)比大多数智能优化方法具有更好的性能，但是它并不适合处理高复杂度的函数。而如何改善全局搜索和局部收敛之间的平衡则是提高灰狼算法性能的重要方向之一[18]。

在灰狼算法中，算法的优化过程是由每代种群中最优适应度的三个解(α、β、δ)指导ω狼搜寻、包围和攻击猎物来完成。

首先，灰狼搜索猎物并逐渐包围过程的数学描述为

D=|CXp(t)-X(t)|

(13)

X(t+1)=XP(t)-AD

(14)

A=2ar-aI

(15)

C=2r

(16)

ri=rand(0,1)

(17)

式中：t为当前迭代次数；C为协同系数向量；A为收敛系数向量；a为迭代中的收敛因子，在整个算法迭代寻优中，它的数值由2线性递减到0；XP(t)为灰狼在第t次迭代时的位置向量；X(t)为第t次迭代后猎物的位置；r为各元素在[0,1]的随机向量；I为单位向量。

其次，通过不断更新α、β、δ狼位置，最终确定猎物位置。灰狼群捕猎过程的数学描述为

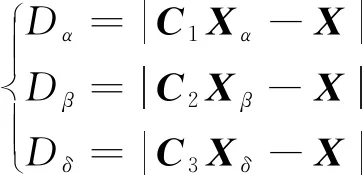
(18)

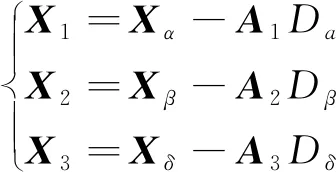
(19)

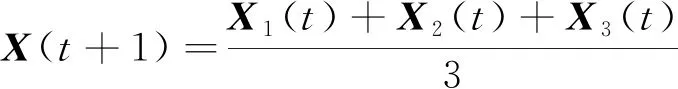
(20)

式中：Xα、Xβ、Xδ为当前种群中α、β、δ的位置向量；Dα、Dβ、Dδ分别为当前灰狼与α、β、δ狼的距离；X表示当前灰狼的位置；A1、A2、A3为收敛系数；X(t+1)为下一代灰狼的位置。

灰狼算法的全局搜索和局部收敛之间的转换取决于收敛因子a和收敛系数A的自适应值[19]。当|A|≥1时，灰狼处在搜寻和包围猎物这个阶段，此时算法具有很强的全局搜索能力。当|A|≤1时，头狼指挥灰狼攻击猎物，此时算法开始进行收敛，其收敛能力较强。控制灰狼算法各个阶段的参数A由收敛因子a决定，而参数a的数值是从2到0线性递减的，a数值随迭代次数线性递减的方式无法切实体现灰狼算法全局搜索和局部收敛这两个阶段的特点。为了增强灰狼算法中每个阶段相应的能力，采用一种改进型收敛因子函数形式，如式(21)所示：

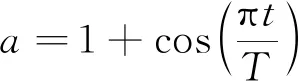
(21)

式(21)中：t为当前已经迭代的次数；T为设定的最大迭代次数。在全局搜索阶段，相比于原始收敛因子a，新函数的收敛因子数值普遍大于原始值，意味着该算法在此阶段具有更强的探索能力。而新函数计算值在局部收敛阶段比原函数值更小，此时算法能实现更快收敛。

此外，在更新候选狼的重要策略上，由于原始GWO算法中的候选狼位置仅仅是通过三只最优个体狼位置的简单加权平均来更新的，并没有充分利用到α、β和δ狼之间的严格等级制度这一关系，基于此，提出一种具有最佳个体权重的α、β和δ平均策略，通过各自的适应度值来计算其相应权重，如式(22)、式(23)所示：

(22)

(23)

式中：fiti(i=α,β,δ)为相应个体的适应度值；X1(t)、X2(t)、X3(t)为最优个体α、β、δ的位置；X(t+1)为下一代候选狼的位置。

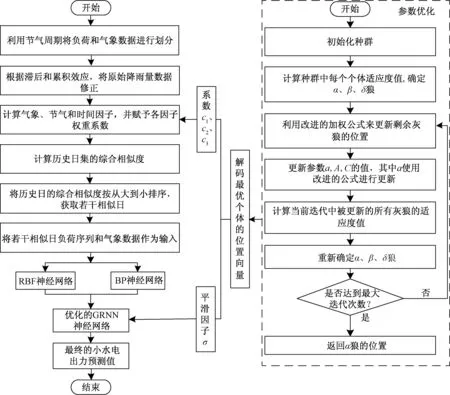
图3 基于节气划分的改进灰狼优化混合参数的小水电出力预测模型Fig.3 Small hydropower output prediction model based on improved grey wolf optimized hybrid parameters in solar term division

2.4 基于自适应相似日的改进灰狼优化混合参数的小水电出力预测模型

根据上文所提自适应相似日选取方法和GRNN非线性组合预测模型，采用改进灰狼算法对自适应相似日中的权重和GRNN中的平滑因子进行优化。改进灰狼算法优化混合参数的小水电出力预测模型的主要步骤如下。

步骤1收集原始小水电负荷和相应气象数据。

步骤2根据节气的时间周期将负荷和气象数据进行划分。

步骤3根据降雨量对小水电的滞后和累积效应，将原始降雨量数据进行修正。

步骤4引入气象因子、节气因子和时间因子，分别计算各因子的相似度并赋予各因子权重系数c1、c2、c3。

步骤5利用改进的GWO优化各因子权重系数c1、c2、c3和GRNN的平滑因子σ，得到最佳模型。

步骤6利用BP和RBF神经网络分别进行预测，得到两组预测值。

步骤7将两组神经网络预测值作为优化后的GRNN输入变量进行非线性组合预测，得到最终小水电出力预测值。

上述提出的小水电组合模型的预测流程如图3所示。

3 实验描述及结果分析

3.1 实验描述

从某地区选取2016年和2017年的小水电负荷出力数据和气象数据，负荷数据、降雨量数据的时间分辨率分别为15 min、1 d。为了验证所提基于节气划分的改进灰狼优化混合参数的小水电出力预测模型可用性，分别从选取相似日和组合预测这两部分进行实验。

3.1.1 实验1

该实验用于验证自适应相似日选取方法的有效性，利用文献[3]所用的相似日选取方法进行对比。选取2017年6月10日作为预测日，用上述两种方法分别进行相似日选取，各自选取出5条相似日负荷曲线。结果如图4和图5所示。

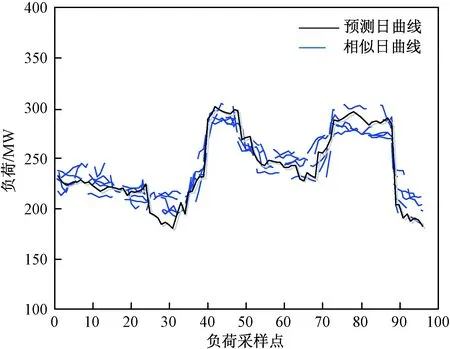
图4 常规相似日与预测日曲线对比Fig.4 Comparison of conventional similar day and forecasting day curves

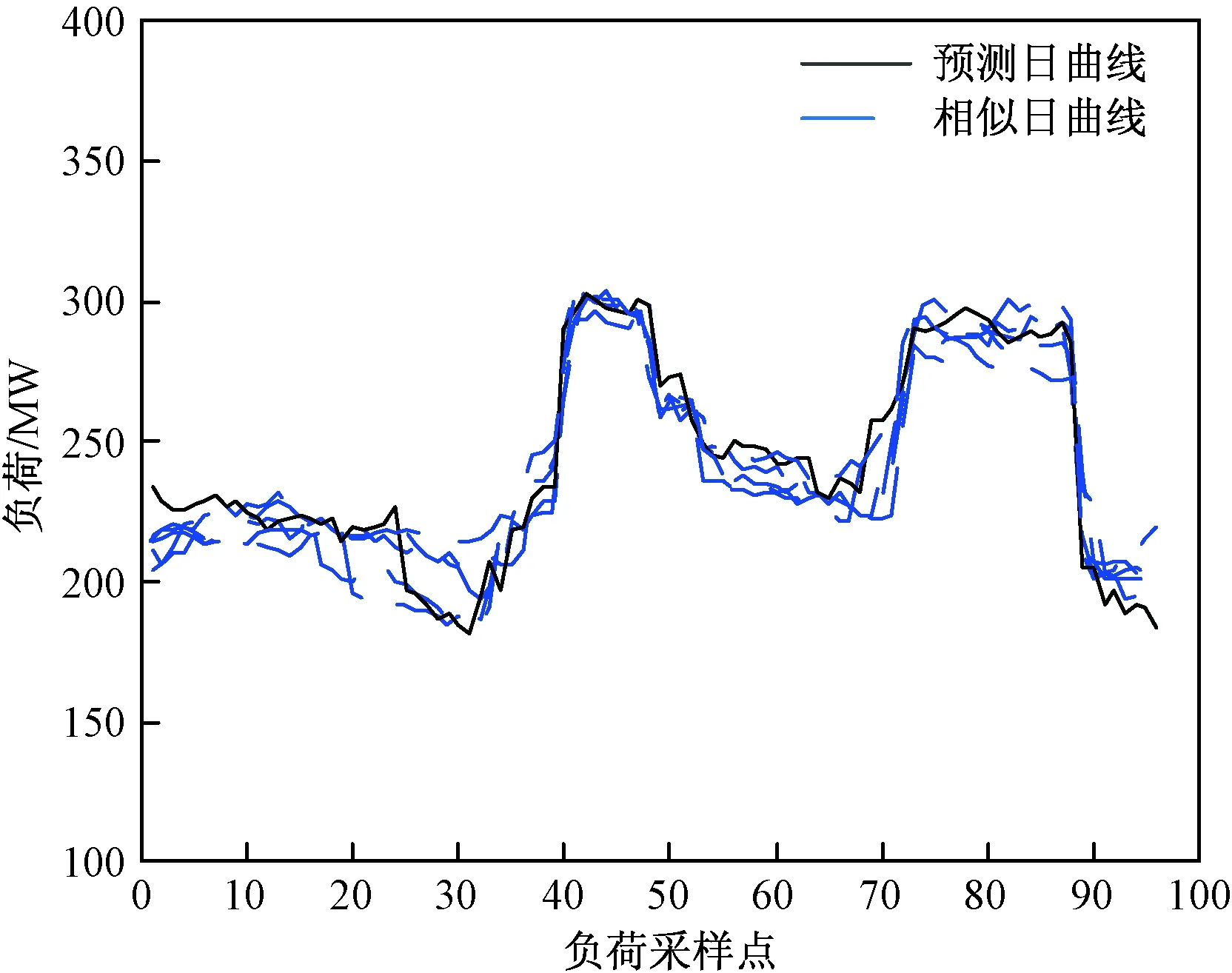
图5 自适应相似日与预测日曲线对比Fig.5 Comparison of adaptive similar day and forecasting day curves

由图4和图5可以看出，由于小水电的随机性较强，用上述两种方法分别得到的5条相似日负荷曲线也不能与预测日曲线完全贴合，但是图5中的相似日曲线更贴近于预测日，在预测日曲线附近上下波动，变化趋势也基本吻合。

3.1.2 实验2

对某地区实际小水电出力机组进行预测，来验证本文方法的有效性。采用改进GWO-GRNN建立组合预测模型，对2017年6月10日小水电出力进行预测。为更好展示结果，设置对比方法为BP神经网络、RBF神经网络、原始GRNN组合预测三种预测模型。图6为预测结果。

从图6可以看出，GRNN组合预测模型与GWO-GRNN组合预测模型比单一BP、RBF神经网络有更高的预测精度，而GWO-GRNN相比于GRNN预测模型，在预测曲线的峰谷段能更好地贴近真实值，预测精度更高。

3.2 误差分析

采用均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)分别作为评价指标，计算公式为

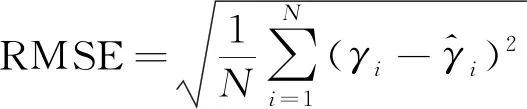
(24)

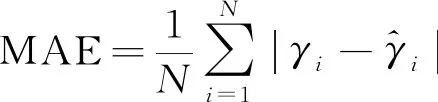
(25)

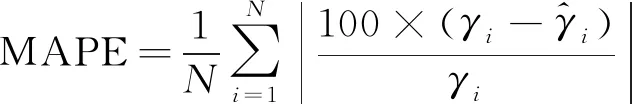
(26)

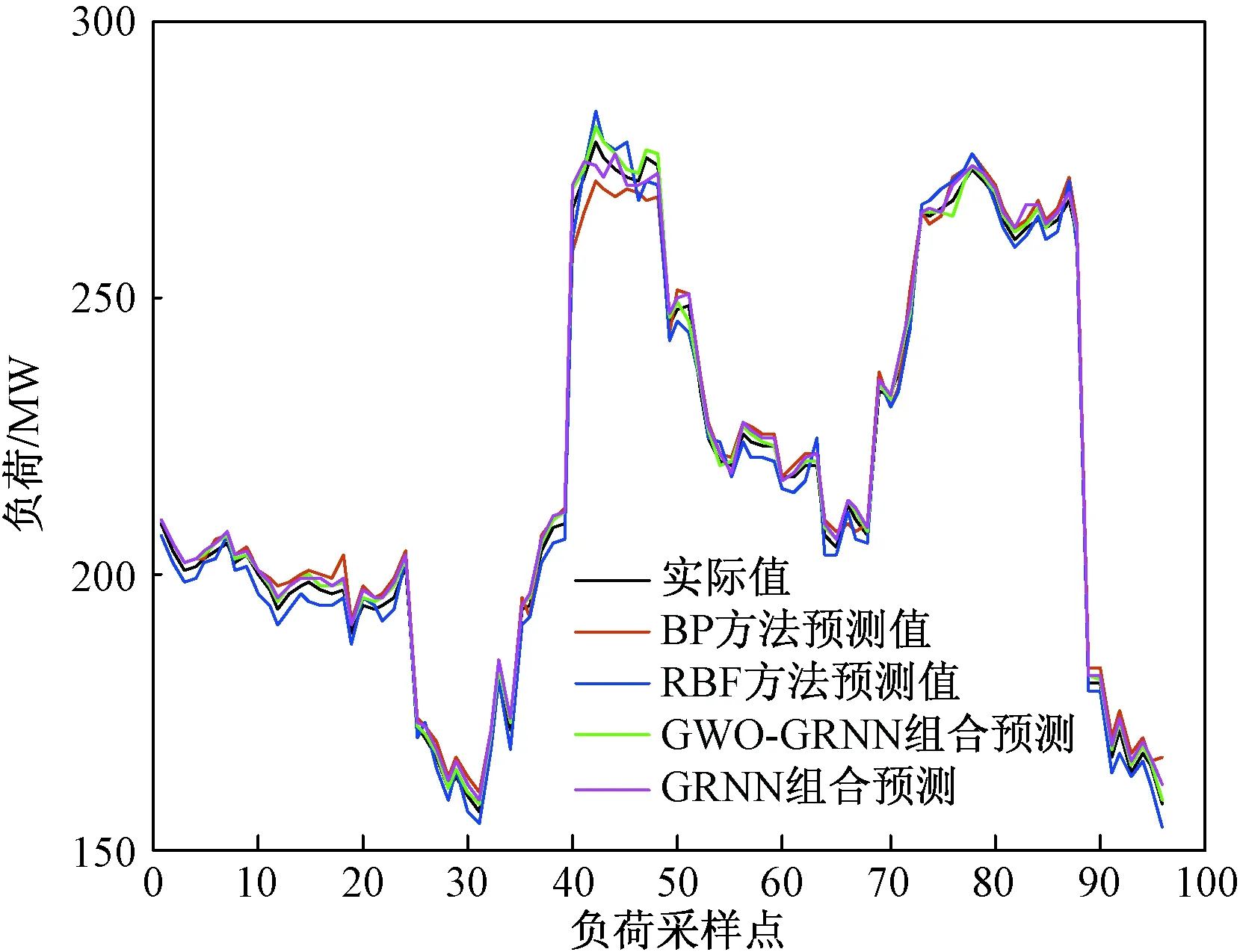
图6 预测负荷曲线与实际负荷曲线对比Fig.6 Comparison of predicted load curve and actual load curve

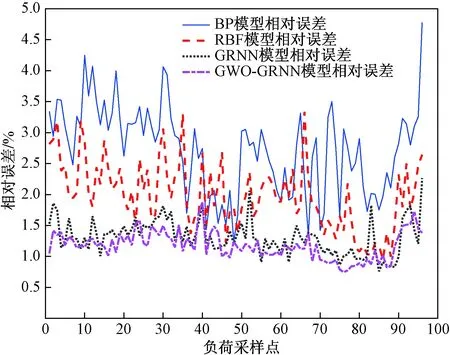
图7 各方法相对误差对比Fig.7 Relative error comparison of different methods

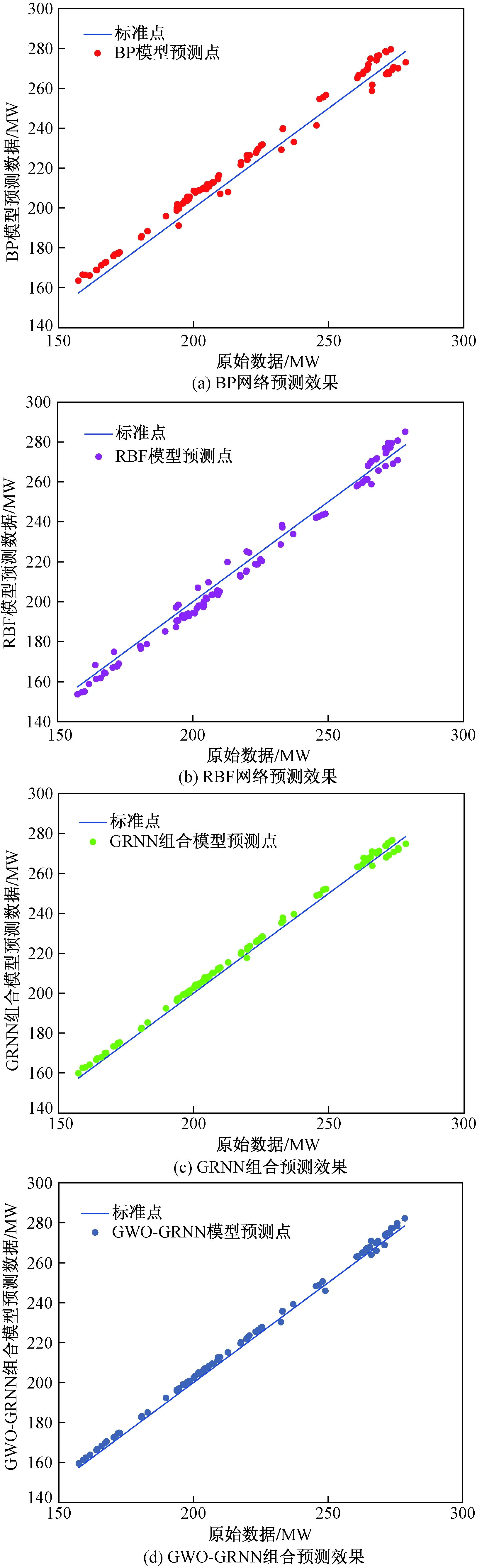
图8 各预测模型的预测效果Fig.8 Prediction effect of each prediction model

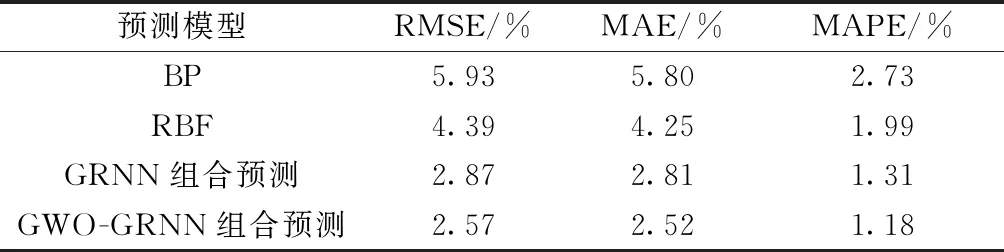
表1 预测结果比较

由图7、图8和表1可以看出，相对于BP、RBF神经网络，组合模型预测精度有所提升，GRNN组合预测的均方根误差、平均绝对误差和平均绝对百分比误差相比于BP网络分别减少了3.06%、2.99%和1.42%，相比RBF网络分别减少了1.52%、1.44%和0.68%，在一定程度上可以说明该非线性组合预测方法可以更有效地预测小水电发电负荷；而预测效果最佳的是GWO-GRNN组合预测方法，其均方根误差、均绝对误差和平均绝对百分比误差比GRNN组合预测分别降低了0.3%、0.29%和0.13%，分析得出GWO-GRNN具有更好的非线性组合能力，预测精度更高。