植被效应对放射性核素弥散影响的模拟研究

陈黎伟 郑兴琪 鲍 杰 陈梦娇 吴家丽

1（合肥师范学院计算机学院 合肥230601）

2（中国科学院合肥物质科学研究院核能安全技术研究所 合肥230031）

植被效应对大气阻流作用主要受枝叶组成的植被屏障所控制［1］。因而，植被效应下的放射性泄漏事故会随着叶密集度不同而呈现放射性物质弥散趋势的差别，对应急抢修人员评估辐射危害造成一定的困难［2］。模拟和分析事故后果是辐射事故后果评价的关键技术之一，而放射性核素弥散模型是模拟和分析事故后果的重要工具［3］。计算流体力学（Computational fluid dynamics，CFD）方法被广泛用于10 km范围内的复杂几何边界、多孔介质流动等复杂环境中的污染物弥散问题，如室内污染物弥散［4］、街道峡谷污染物弥散［2］、自由表面污染物弥散［5］等。对于植被效应下的污染物弥散问题，国内外研究人员将其描述为多孔介质效应下的污染物弥散［2，6］，利用该方法可以较为准确地描述植被对于大气流动的压力损失效应，从而模拟植被条件下的放射性核素分布。

近年来，国内外研究人员在道路交通、铀矿开采、乏燃料公路运输等不同行业领域对植被效应下的污染物弥散问题进行研究。Ghasemian等［6］研究了交通污染物在植被效应下的扩散规律，并给出了城市规划建议；Wang 等［7］和Jeanjean 等［8］的工作从植被、街道间距和叶密集度等不同角度研究了植被条件下的街道峡谷中交通所产生的大气污染物分布规律；谢清芳等［9］针对不同植被覆盖面积研究了铀尾矿库氡气的迁移和扩散分布规律；陈黎伟等［10］模拟了乏燃料公路运输事故条件下放射性核素分布规律，研究了在有无树木环境下的放射性核素弥散分布规律。

然而，由于不同植被种类和季节变化所产生的植被效应具有显著差异，本文考虑植被条件下的不同压力损失系数，基于CFD 方法模拟了放射性核素弥散分布规律，是文献［10］工作的进一步拓展，期望可以为核应急工作者提供更为精确的参考依据。

1 模型及验证

为较为准确地获取植被效应下的放射性核素浓度分布规律，由于湍流标准k-ε 模型适用于外部流动，计算过程中表现稳健［11］。该模型从大气流场和放射性核素浓度场两个部分进行求解。假设植被效应下的空气为不可压缩流体，在植被效应下的放射性泄漏场景中，通过引入动量源损失因子修正动量守恒方程，以获得植被效应下的风场分布，泄漏的核素除了受到植被效应影响外，还受到放射性衰变和沉积效应等影响。

修正后的动量守恒方程可表示为式（1）。

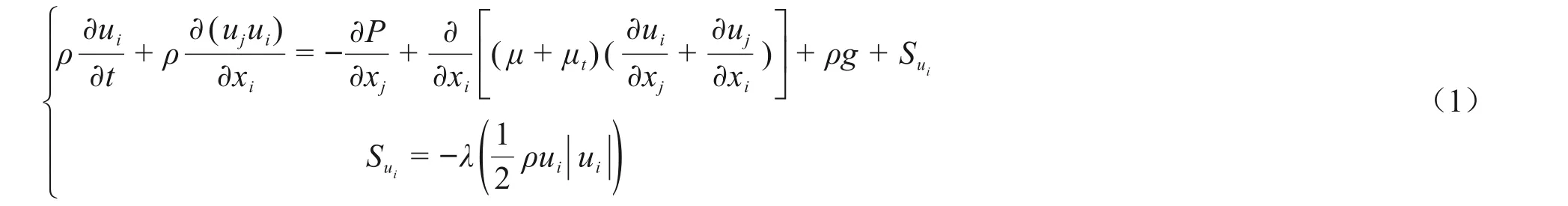
式中：xi表示三维笛卡尔坐标系下的坐标轴（i=1，2，3 分别表示x，y，z 方向）；ui（m/s）代表气流速度分量；ρ（kg/m3）表示大气密度；t（s）表示时间；p（Pa）表示大气压力；μ、μt（kg/（m∙s））分别表示动力粘度及湍流粘度；g（m/s2）表示重力加速度；λ（m-1）代表压力损失系数。

放射性核素浓度方程可表示为式（2）。

式中：C（kBq/m3）表示单位时间步对应坐标位置的浓度值；ΓC（m2/s）为湍流扩散系数；SC（kBq/（m3·s））为放射性泄漏源项；λd为衰变因子（通常表示为0.693/T1/2，T1/2（d）为放射性核素半衰期）；vd为沉积因子。

文中计算方法采用压力速度耦合算法对大气风场进行稳态求解，然后将稳态风场作为初始条件求解放射性浓度方程，得出泄漏后的放射性核素浓度分布［2］。以文献［8］中验证模拟的数据作为验证，验证结果与文献［8］中的结果具有良好的一致性，相关详细的模型验证方法参见文献［10］。

2 数值模拟

2.1 场景选择分析

我国乏燃料运输目前主要以公路运输方式为主，在公路运输事故环境中，主要的事故类型可分为碰撞事故和非碰撞事故两类，碰撞事故中碰撞物体可能是固定物体或者非固定物体，非碰撞事故可能由于翻车、机械故障、火灾事故或人因等因素，从而导致容器受损发生核素泄漏［12-14］。从长远看，单一的公路运输模式已不能满足乏燃料增长需求，有专家认为利用铁路运输实现水陆联运是乏燃料运输的较好方案［15］，而脱轨、碰撞、火灾等也会造成铁路运输事故［16-17］。然而，植被环境是公路及铁路运输事故场景的一个重要环境特征，且植被环境会随着季节、种类、覆盖率等发生变化，都会产生不同的植被压力损失，从而对放射性核素弥散规律产生影响。本工作基于以上事故场景的特点，对道路两边植被防护林进行假设，通过压力损失系数描述不同季节及植被种类所产生的植被效应，以描述不同条件下的植被对放射性核素弥散所产生的影响。

2.2 场景描述

2.2.1 植被效应分析

相对于固体壁面效应，植被效应在本质上更加复杂，其主要是由枝叶组成的具有多孔介质特性的透气性屏障［18］。在不同的植被效应下，气流的衰减效果存在较大差别，植被的宽度和疏密程度也对空气流动产生不同的压力损失［19］，因此，压力损失系数是研究植被通透性的良好指标，并且压力损失系数与叶密集度呈正比例关系，其主要通过植被的固定系数与叶密集度来估计［2］，即植被所产生的压力损失随着叶密集度增长而增长，放射性核素弥散在植被效应下会随着不同的压力损失系数而呈现不同的分布趋势。另外，季节更替会导致一些植被发生明显的变化，如在冬天，一些树木的阻力主要来源于树干、树枝，视为无植被情况，而春天叶的生长和秋天叶的脱落情况会随着不同树种、不同季节发生变化。阔叶树种在我国道路防护林中较为常见，从文献［19］中得出部分的阔叶树种压力损失系数范围一般在0～15 m-1。

为体现不同植被环境下的影响所产生的压力损失，文中压力损失系数分别取0.1 m-1、0.5 m-1、2.0 m-1、8.0 m-1，以观察不同植被效应所带来的影响。考虑泄漏源的高度在2 m位置，以表示路面高于两边植被泄漏的情形。为了向核应急工作者提供辐射防护参考，在讨论中以工作场所的131I 最大允许浓度为0.33 kBq/m3为假设条件进行考虑［2］。

2.2.2 场景假设

场景的几何模型如图1所示，假设场景计算模型为1 000 m（x 方向）×1 000 m（y 方向）×100 m（z方向），植被防护林位于模型的中间部分，该防护林分别由植被群一和植被群二组成，宽度（x方向）和高度（z 方向）均为30 m，长度（y 方向）为200 m。植被防护林中间为道路及空旷场地，其宽度是60 m，气流沿x正向垂直于植被防护林方向经过。

图1 放射性泄漏事故场景几何模型Fig.1 Geometry of scenario under the radioactive leakage accident

假设发生泄漏事故当天气温20 ℃。事故发生在植被防护林之间的正中心位置，考虑放射性核素131I 连续泄漏1 h，泄漏率为3.3 （ kBq/m3）/s，其半衰期为8.02 d，干沉积量可忽略不计。沿x 正方向的气流参考风速为4 m/s，将第二类边界条件诺伊曼边界条件作为壁面边界，以表示通量的法向导数在边界上指定［20］。近地层环境入口垂直剖面通过公式（3）～（5）对平均速度（U（z）、湍流动能（k）以及湍流耗散率（ε）进行指定［2］。

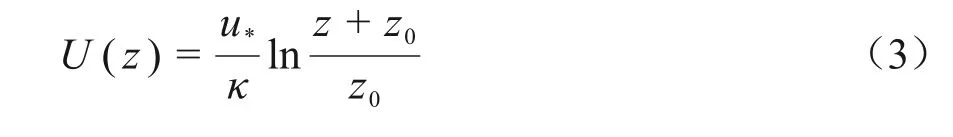
式中：摩擦速度u*=0.4 m/s；冯卡曼常数κ=0.41；地面粗糙度z0=0.1 m。

2.3 网格无关性验证

网格数量级倍差在污染物模拟的网格无关性验证中一般的取值范围在1.2～1.5，从而达到工作中所需的分辨率［8-9］。文中采取1.2×105、1.8×105及2.7×105三类网格数进行无关性测试。图2为y=500 m、z=2 m 处， x=480～700 m 的第1 800 秒放射性核素浓度分布。结果表明，相对于1.2×105网格，1.8×105网格与2.7×105网格计算结果曲线的一致性更好。因此，下面模拟采用1.8×105网格数来模拟，以保证精度的基础上提高计算效率。

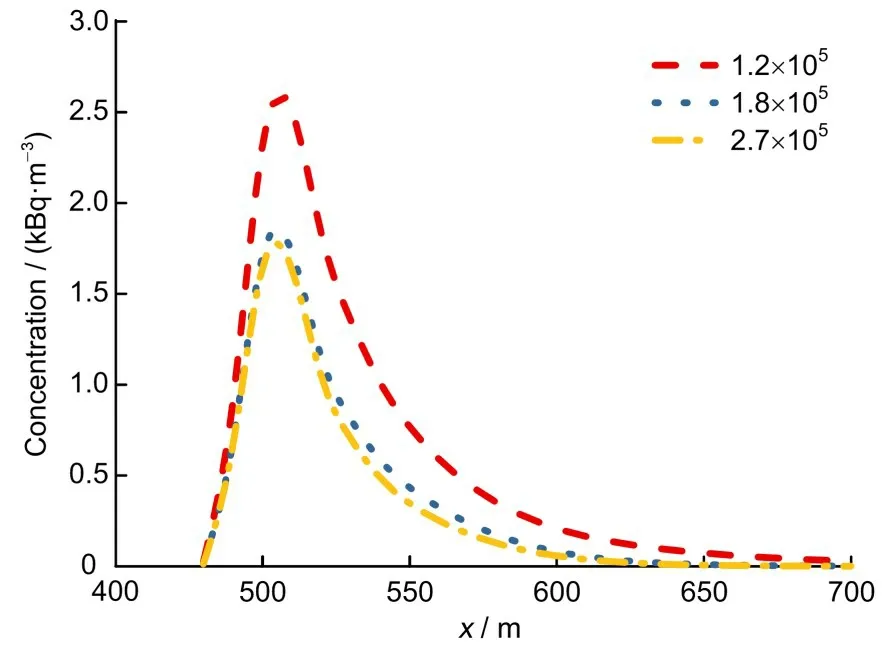
图2 放射性核素浓度（y=500 m，z=2 m，x=480 ～700 m，第1 800 秒）Fig.2 Concentration of radionuclide(y=500 m,z=2 m,x=480 ～700 m,the 1 800th second)

2.4 分析与讨论

为了获取不同压力损失系数的植被环境下的放射性核素弥散规律，以下围绕放射性浓度方程（式（2））所计算的泄漏后1 h的分布状态进行讨论，其主要从泄漏位置平面上植被的不同压力损失系数条件下的风场分布、放射性核素浓度分布、风速分布曲线及放射性核素浓度曲线进行对比分析。

图3表示植被所产生的不同压力损失系数下第3 600 秒、y=500 m 平面风场与放射性核素浓度分布对比情况，图3（a）～（d）分别表示压力损失系数为λ=0.1 m-1、0.5 m-1、2.0 m-1、8.0 m-1。其中，图左侧所表示的是风场分布，右侧为放射性核素浓度分布，虚线框为植被区域。随着压力损失系数的增大，植被附近的风场分布呈现了不同的变化，从而使放射性核素弥散分布状态差别较为显著。

首先，由图3（a）、（b）可以看出，λ=0.1 m-1时，气流沿去流方向流动，但受到植被效应的影响，风速得到了减弱；当λ增加到0.5 m-1时，植被群二的右侧附近出现了较大涡旋。因此，在植被的影响下，放射性核素浓度弥散趋势因压力损失系数的增大，其水平方向弥散距离缩小明显，分布状态逐渐由去流方向的扁平状逐渐转变为释放源附近类半圆状，这表明植被压力损失系数的增加对去流方向的放射性核素水平方向弥散范围起到了明显的抑制作用，但也造成了植被群间的纵向放射性污染范围的扩大。其次，由图3（b）、（c）、（d）可以看出，相比于λ=0.5 m-1，压力损失系数增加到2.0 m-1时，植被群之间的风场开始出现涡旋，放射性核素水平方向弥散距离在缩小的同时，释放源周边的放射性核素浓度逐渐形成较为均匀的半圆分布状态，这主要是受到植被群间涡旋的影响，放射性核素在释放过程中开始均匀向四周进行弥散。然而，相比于λ=2.0 m-1，当压力损失系数增加到8.0 m-1时，放射性核素分布状态变化并不明显。

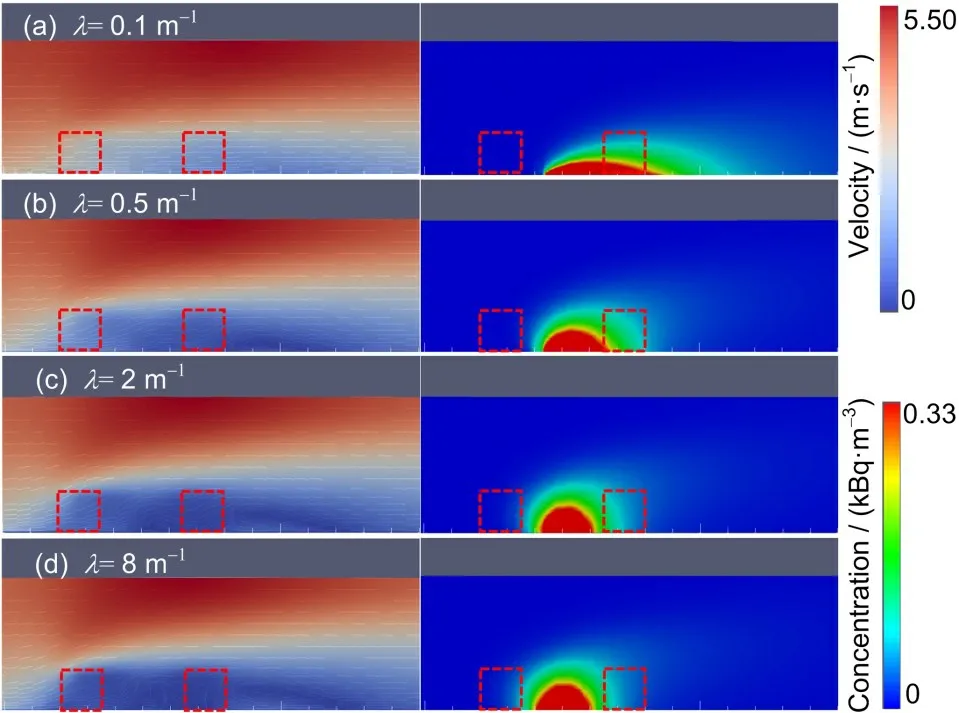
图3不同压力损失系数下风场与放射性核素浓度分布（y=500 m，第3 600 秒）Fig.3 Distribution of wind field and radionuclide under different pressure loss coefficients(y=500 m，the 3 600th second)

为了进一步观察植被效应对放射性核素弥散规律的影响，图4 提取了不同压力损失系数下第3 600 秒、释放源高度在y=500 m 平面上的风速和放射性核素浓度情况，图4（a）表示x=400～700 m区间的风速，图4（b）表示x=480～700 m 区间的浓度。其中，水平方向的植被范围分别位于440 m≤x≤470 m和530 m≤x≤560 m区间内，当风速大于0 m/s时，表示气流沿去流方向移动，当风速小于0 m/s时，表示气流沿来流方向移动。从图4 可以看出，当λ=0.1 m-1时，400 ～700 m区间的风速虽然因植被影响而减小，但气流均沿去流方向移动，也进一步说明了图3（a）的放射性核素随去流方向的扁平状弥散分布状态；当λ=0.5 m-1时，位于植被群二的右侧（x＞560 m）有一部分区间的气流速度小于0 m/s，即水平方向气流沿来流方向移动，这表明当泄漏位置的放射性核素弥散到植被群的右侧时会受到反方向（沿来流方向）气流影响，从而限制了放射性核素向去流方向弥散趋势。当λ=2.0 m-1和λ =8.0 m-1时，位于植被群区间（470 m≤x≤530 m）的风速在0 m/s左右附近波动，因此泄漏源附近的风速较小，且风向不定，从而导致了植被群之间的放射性核素蓄积且缓慢均匀的向四周弥散，因此，当压力损失系数大于2.0 m-1时，植被效应下的放射性核素弥散分布逐渐趋于稳定。

图4 不同压力损失系数下释放源的风速（a）和放射性核素浓度（b）（y=500 m，第3 600 秒）Fig.4 Wind speed(a)and radionuclide concentration(b)under different pressure loss coefficient(y=500 m，the 3 600th second)

3 结论

文中对不同压力损失系数的植被效应下放射性核素弥散趋势进行模拟，得到以下结论：（1）一定范围内的植被压力损失系数条件下的植被群附近的风场分布呈现明显不同，对放射性核素弥散分布状态影响较大，分布状态逐渐由去流方向的扁平状转变为释放源附近半圆状，由横向弥散逐渐转变为四周弥散；（2）植被压力损失系数增加到2.0 m-1时，受到植被群间涡旋的影响，放射性核素开始缓慢均匀向四周弥散，从而抑制了水平方向弥散范围；（3）当压力损失系数大于2.0 m-1时，由于植被群间涡旋作用，放射性核素在释放过程中分布状态趋于稳定，此时压力损失系数增加对放射性核素弥散趋势影响并不显著。因此，对于植被效应下的放射性泄漏事故，首先应对不同植被环境进行评估，再根据植被叶密集度情况初步估计压力损失系数，模拟其放射性核素弥散趋势。另外，还可以通过不同泄漏源位置假设对不同的植被效应下的变化进行模拟，也会呈现不同的变化趋势，为植被效应下的早期辐射事故应急提供更精确的信息，以帮助应急决策者做出合理的决策。