基于PSO-NARX网络的涡轴发动机稳态模型辨识
2021-05-06李本威钱仁军滕怀亮
董 庆,李本威,钱仁军,滕怀亮,张 赟
(1.海军装备部驻苏州地区军事代表室, 江苏 苏州 215000;2.海军航空大学 航空基础学院, 山东 烟台 264000)
航空发动机是一个复杂的非线性时变系统[1]。在发动机故障诊断[2]、性能分析与仿真及其控制规律设计[3]等多个领域,发动机模型都发挥着无可代替的作用。针对装配某型涡轴发动机的直升机将在不同大气环境(高原、高空及高低温等)下进行飞行试验的相关工作,为实现对发动机状态的实时监控和对发动机稳态控制规律的进一步研究,建立精度和实时性均满足实际要求的发动机稳态模型成为相关工作关键的一环。
目前,航空发动机模型建立的方法主要有两种:一种是分析部件气动特性、机械关系的解析法,另一种是系统辨识的方法。解析法通过假设、近似处理和大量的迭代运算来获取发动机的性能数据,过程复杂。而系统辨识的方法无需了解发动机复杂的部件特性,只需足够的发动机输入输出参数即可快速建立精度满足要求的发动机模型。目前,基于数据驱动的模型辨识方法得到快速的发展,常用的辨识方法有最小二乘法[4]和子空间状态辨识法[5]等。它们假设发动机是线性时不变系统,导致建立的发动机动态模型精度不能达到很好的效果。近几年,人工神经网络[6]。(artificial neural networks,ANN)、支持向量机[7](support vector machine,SVM)和极限学习机[8]。(extreme learning machine,ELM)等机器学习算法快速发展,具有了很好的非线性学习能力,很多人也将它们应用到航空发动机模型的建立。陈超等[9]利用RBF神经网络对航空发动机起动模型进行辨识与仿真;王海涛等[10]利用稀疏最小支持向量机建立发动机动态过程模型。这些传统的神经网络存在初始参数选择无依据、无反馈单元等各种问题。耿宏等[11]利用NARX网络建立发动机参数动态辨识模型;Pogorelv等[12]利用动态神经网络对双轴燃气轮机差分形式的非线性动态模型进行辨识,并应用于启动控制。NARX网络具有反馈延时单元,具有很好的动态特性,且对非线性动态系统具有良好的非线性逼近能力,效果明显优于前馈神经网络,但是网络初始特性参数由随机函数产生影响辨识模型精度。
粒子群优化算法(particle swarm optimization,PSO)稳定性好且具有较好的全局搜索和寻优能力,利用PSO对NARX网络的初始参数进行寻优,使得NARX网络取得更好的效果。文献[13]验证了粒子群优化算法的优越性。文献[14]验证了NARX网络对非线性动态系统具有良好的非线性逼近能力。
针对以上分析,本文以直升机飞参数据为驱动,结合提出的三点自适应判断法从飞参数据中提取发动机稳态数据样本,采用PSO-NARX方法对涡轴发动机稳态模型进行辨识。利用样本之外架次的飞参数据对辨识模型的性能进行验证并与其他不同辨识算法相比较。结果表明本文PSO-NARX方法对涡轴发动机稳态模型辨识的可行性与优越性,为后续在高原、高空及高低温环境条件下进行飞行试验的此型涡轴发动机状态实时监控和控制规律的优化奠定基础。同时,也为工厂对此型涡轴发动机即将开展的试车试验提供相关支持。
1 基于PSO的NARX网络原理
1.1 NARX网络模型
英文缩写词NARX(nonlinear auto regressive with exogenous inputs model)的意思为有外部输入的非线性自回归模型,是线性外生输入的自回归(ARX)模型改进后在非线性情况下的应用。其通过添加延时单元使过去某些时刻的输入、输出成为模型的输入,再利用多层感知器的非线性映射能力,来实现时间序列的动态预测[11]。NARX模型可由带有外部输入的非线性差分方程表示为
y(t+1)=f[y(t),y(t-1),…,y(t-k),
x(t),x(t-1),…,x(t-m)]
(1)
式中:f表示自变量的一个非线性函数 ;y(t-k)表示输出参数相应时延为k的数值;x(t-m)表示输入参数相应时延为m的数值;y(t+1)表示得到的下一时刻的输出数值。NARX网络模型见图1。
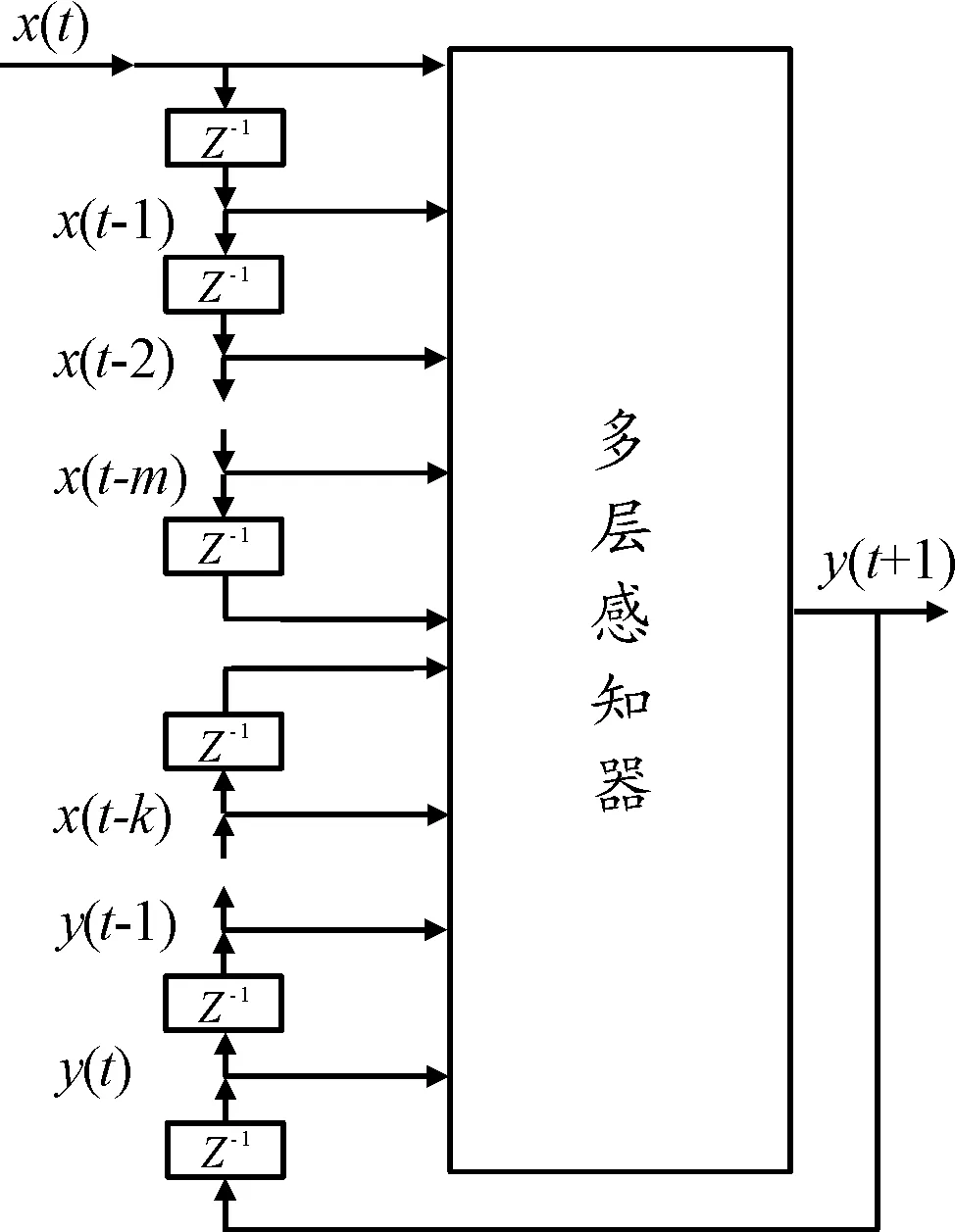
图1 NARX网络模型示意图
某t时刻其第i个隐含层节点的输出di(t)为
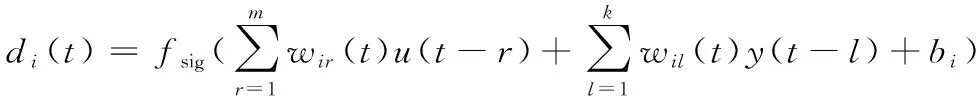
(2)
式中:fsig为隐层节点使用的双曲线正切sigmoid函数;wir(t)、wil(t)为t时刻第i个隐层节点与输入u(t-r)、输出y(t-l)之间的权值;bi为第i个隐层节点的偏置。第j个输出层节点输出y(t)为
(3)
式中:wij(t)为t时刻第i个隐层节点到第j个输出层节点的权值;Tj为第j个输出层节点偏置;N为隐含层节点个数。
1.2 粒子群优化算法(Particle Swarm Optimization)
粒子群优化算法属于进化算法的一种,源于对鸟群捕食的行为研究。该算法从随机解出发,通过迭代找到最优解,通过适应度来评价解的品质,并通过追随当前搜索到的最优值来寻找全局最优[16-17]。
每个粒子都有位置xi和速度vi两个属性,在每次的迭代中,粒子通过跟踪个体极值和全局极值来更新自己。假设在一个D维的目标搜索空间中,即每个粒子(解)都是一个D维的向量,粒子群由N个粒子构成,则其中第i个粒子位置可以表示为
xi=(xi1,xi2,…,xiD),i=1,2,…,N
第i个粒子的速度也是一个D维的向量,记为
vi=(vi1,vi2,…,viD),i=1,2,…,N
并设定第i个粒子迄今为止搜索到的最优位置为个体极值,记为pi,而整个粒子群迄今为止搜索到的最优位置为全局极值,记为pg。同样,pi、pg均为D维向量。在找到这两个最优值后,粒子通过下面的公式(4)来更新自己的速度和位置。
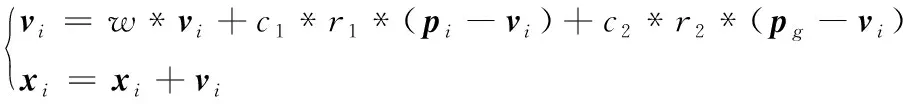
(4)
式中:c1、c2为惯性因子和学习因子,也称加速常数,反映粒子间信息交换的强度,通常取c1=c2=2,r1、r2为[0,1]范围内的均匀随机数,pi为第i个粒子迄今为止搜索到的最优位置,即个体极值,pg为整个粒子群迄今为止搜索到的最优位置,即全局极值。
目前多采用的使线性递减权值策略,动态w能够获得比固定值更好的结果。w的引入使得PSO算法性能有了很大的提高,提高了算法的全局和局部的搜索能力,w的值为
w=(wini-wend)(Gk-g)/Gk-wend
(5)
式中:Gk为最大迭代次数;wini为初始惯性权值;wend为迭代至最大进化代数时的惯性权值,典型权值wini取0.9,wend取0.4[17]。
1.3 基于PSO的NARX网络特征参数优化流程
NARX网络结构将隐含层个数设定为1,隐含层神经元个数q值的经验公式为
(6)
式中:d为输入层节点数;l为输出层节点数;a为10~14的常数。
利用PSO优化NARX网络中输入层到隐含层的权值vih,隐含层到输出层的权值whj,隐含层神经元的偏置bh,输出层神经元的偏置bj,i=1,2,…,d;h=1,2,…,q;j=1,2,…,l。以下是具体的优化流程:
步骤1:初始化。初始化粒子群群体数量N,种群数量和最大迭代步数。每个粒子mi由vih、whj、bh、bj组成:
mi=(v1h,v2h,…,vih,w1j,w2j,…,whj,b1,b2,…,bj,b1,b2,…,bh)
利用rands函数初始化每个粒子mi的xi和vi,xi和vi中的每个元素的取值范围都在[0,1]之间。
步骤2:计算每个粒子适应度的值。将模型预测输出与目标输出的均方误差作为粒子的适应度函数值,如式(7)所示,均方误差用来评价模型与实测数据的吻合程度,PSO算法寻优的目标就是使粒子的适应度函数值即均方误差最小。
(7)
式中:Emse(y,yd)为均方误差;y(t)为模型的预测值;yd(t)为输出实测值。
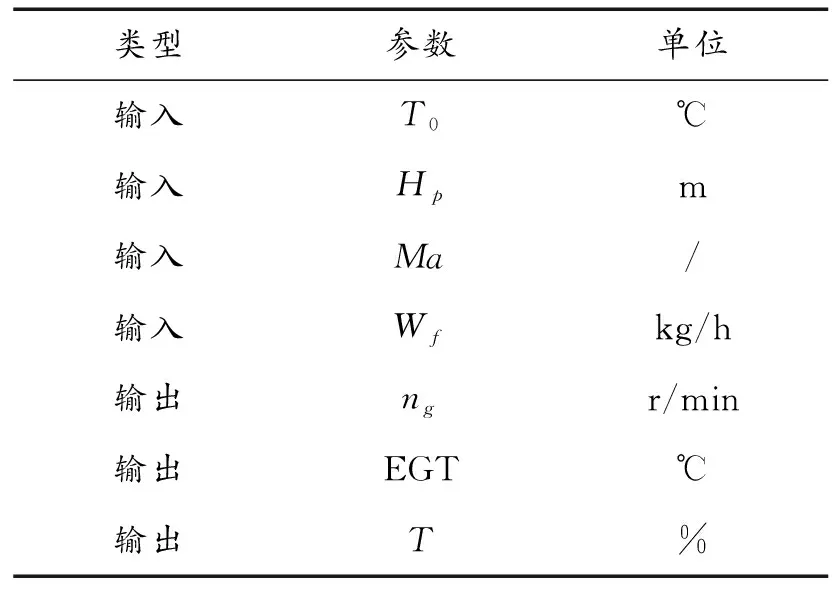
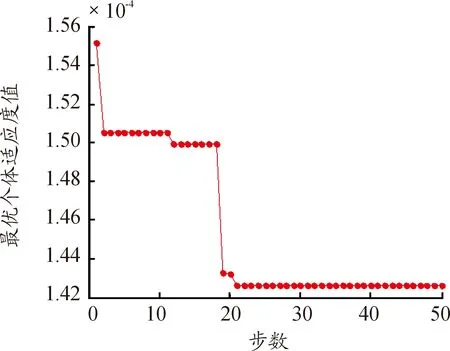
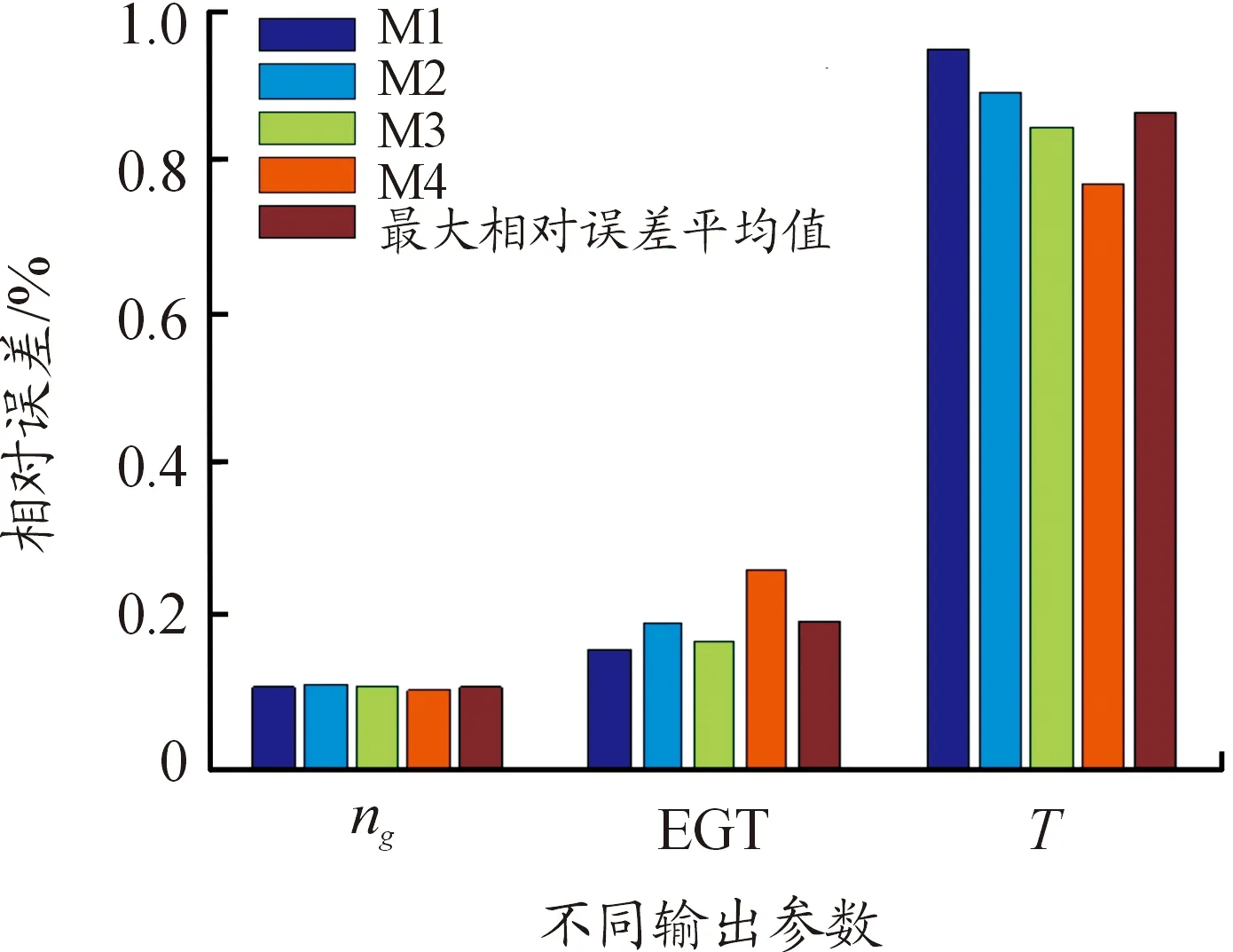
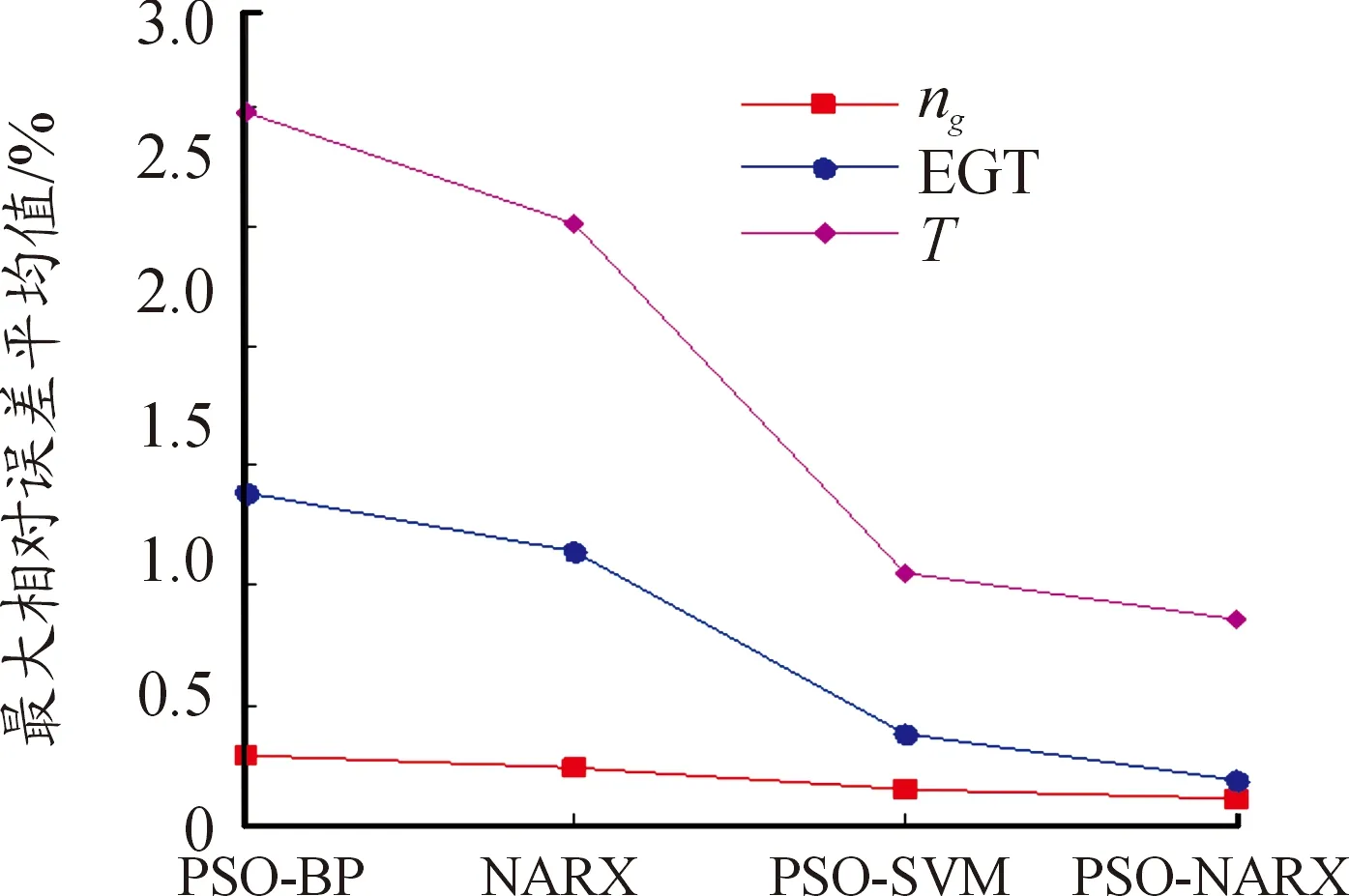
步骤3:计算每个粒子,用它的适应度值ffitness(mi)和个体极值pi比较,如果ffitness(mi) 步骤4:重复步骤1~3直到最大迭代步数,利用PSO算法得到NARX网络的特征参数。 航空发动机是一个高度非线性的时变系统。大气静温T0、绝对气压高度Hp、飞行马赫数Ma、燃油流量Wf都会影响发动机工作过程。涡轴发动机主要工作状态参数为燃气发生器转速ng、发动机排气温度EGT和发动机扭矩T。 发动机当前时刻的工作状态与过去时刻的工作状态密切相关。涡轴发动机稳态模型的输入参数设置为T0、Hp、Ma、Wf的当前时刻值与过去时刻的值以及ng、EGT和T过去时刻的值,输出参数设置为ng、EGT和T的当前时刻值。涡轴发动机稳态模型输入输出参数如表1所示。 综上,涡轴发动机稳态模型为: (8) 式中:fss为需要辨识的发动机模型;k、m为输入输出延时阶次。文献[18]提出:通常,发动机模型输入输出参数延时阶次设置为2为最佳方案。因此,将k和m设置为2。 表1 发动机稳态模型输入输出参数 根据表(1)知输入层节点数d为4,输出层节点数l为3,根据式(6)得到本文NARX网络隐含层神经元个数q选为15。 基于PSO-NARX网络的涡轴发动机稳态模型辨识的具体流程如图2所示。 步骤1:根据发动机稳态工作原理,建立涡轴发动机的稳态模型如式(8),包括输入、输出参数和函数关系。 步骤2:利用三点自适应法从大量飞参数据中提取发动机稳态时的数据,建立辨识所需的样本,并对样本进行预处理。 步骤3:设置PSO算法的种群粒子数和最大迭代次数等基本参数,利用PSO对NARX网络的特征参数进行寻优。 步骤4:以提取处理的辨识样本为驱动,利用优选特征参数后的NARX网络对所建立的涡轴发动机稳态模型进行辨识。 步骤5:利用验证样本对辨识得到的稳态模型进行验证。 综上,步骤1~5构成了基于PSO-NARX网络的涡轴发动机稳态模型的辨识方法。 图2 涡轴发动机稳态模型辨识流程框图 以直升机飞参数据为驱动,建立基于PSO-NARX网络的涡轴发动机稳态辨识模型,对辨识模型的性能进行验证并与NARX、PSO-BP、PSO-SVM建立的辨识模型进行对比。 针对从飞参数据中对发动机稳态状态进行识别的问题。本文在此提出一种稳态状态的识别算法——三点自适应判断法。设换算转速-时间序列为向量ng,c(t),稳态转速限制值采用动态变化值δn为 δn=0.01ng,c(t) (9) 采用三点自适应判断法判断第i个点是否为稳态点,将三点数值相减得到: (10) 若Δ<δn,则第i个转速点为稳态工作点,并令ng,c(i+1)=ng,c(i),将时间平移继续进行判断。对符合转速波动的稳态点进行记录后通过稳态的时间限制值δtime,确定发动机的稳定工作状态。根据涡轴发动机大量分析数据、工作经验及其工作特点,通常选取转速限制值为1%,稳态时间限制值为10 s。 使用DBSCAN聚类方法对某一架次飞参数据(飞参数据的采样频率为1s)中1发位置发动机转速去噪处理后[20],利用三点自适应判断法得到此架次稳定状态处理曲线如图3所示,从中可以得出发动机的稳定状态。图3(a)是利用三点自适应判断法得出的稳定状态判断曲线,图3(b)是图(a)中3 000~5 000 s段的局部放大。例如,图3(b)图方框内的ng,c=28 997 r/min(即水平线所对应的换算转速)时的稳定状态即为发动机的稳态点,由此得到此架次此涡轴发动机在装机过程中转速从0~32 400 r/min(最大连续状态)之间所有稳态点。 图3 飞参数据稳态处理曲线 使用同样的数据处理方法对5台直升机2016—2018年的27个架次飞参数据中1发位置发动机转速进行处理,得到同型号涡轴发动机转速从0到最大连续转速之间3 564个稳态点,每个稳态点的数据记为一组样本数据,3 564组辨识样本共129 076个数据点作为涡轴发动机稳态模型辨识样本。此27个架次飞参数据来源于不同工况下的直升机飞行数据,包括低温、高温等多种飞行工况,发动机的工作点几乎涵盖了整个飞行包线。 根据构建的涡轴发动机稳态模型如式(7)所示,确定样本参数为:T0、Hp、Ma、Wf、ng、EGT和T。对选取的样本数据进行滤波和归一化的处理。将处理后的数据作为模型的辨识样本,在模型的训练与验证结束后对数据进行还原。采用辨识模型输出值与飞参数据实测值最大相对误差以及最大相对误差均值来评价建立的辨识模型性能。相对误差Eref为 (11) 式中:y(t)为辨识模型的输出值;yd(t)为飞参数据实测值。 综合考虑计算时间和收敛性以及资源占用的最优值等因素,将PSO算法的最大迭代步数设置为50,种群粒子数量设置为30[21-23]。利用PSO算法对NARX网络特征参数寻优,寻优过程的适应度函数值曲线如图4所示。结合从飞参数据提取的辨识样本,利用PSO算法优化过特征参数的NARX网络对建立的涡轴发动机模型进行回归辨识。 图4 寻优过程的最优个体适应度函数值曲线 利用样本外的4个架次不同编号发动机稳态数据对得到的辨识模型非样本点推广能力进行验证,分别取转速ng,c=25 417、28 703、28 997、30 301 r/min时的4个稳态点数据为4组验证样本,分别记为M1、M2、M3和M4。通过将验证样本输入辨识模型得到的输出值与飞参数据实测值对比来验证辨识模型的性能。例如,以M3组为验证样本时,取M3组中200个连续的数据点,得到辨识模型输出参数ng、EGT和T与飞参数据实测值曲线和相对误差分布曲线如图5、图6、图7所示。 图5 M3为验证样本ng辨识结果曲线 图6 M3为验证样本EGT辨识结果曲线 4组数据分别作为验证样本时得到ng、EGT和T的最大相对误差及最大相对误差均值如图8所示。从图8可以得到,不同验证样本时,输出参数ng、EGT和T的最大相对误差分别为0.11%、0.26%和0.95%,最大相对误差均值分别为0.105%、0.193%和0.865%。从图5、图6、图7、图8可以得到,辨识模型输出结果很好地逼近了飞参数据实测值。说明本文提出的基于PSO-NARX网络的发动机稳态模型精度满足实际应用时的精度要求。 图8 M1 M2 M3 M4为验证样本时输出参数ng、EGT、T误差的直方图 为了更好的说明本文提出的基于PSO-NARX的涡轴发动机稳态模型辨识的优越性,用相同的训练样本和验证样本,利用PSO-BP、PSO-SVM和NARX网络辨识建立的涡轴发动机稳态模型。 BP神经网络使用MATLAB R2014a中的工具箱,设置为输出层、单隐含层和输出层,隐含层神经元个数依据经验公式设置为15,各层连接权值及神经元偏置通过PSO寻优得到,选用Levenberg-Marquardt算法。SVM对涡轴发动机稳态模型进行回归辨识时,利用PSO对SVM特征参数平衡因子C、不敏感度ε和径向基核函数参数σ进行寻优。两种算法中PSO的最大迭代步数均设置为50,种群粒子数量均设置为30。NARX网络使用MATLAB R2014a中的工具箱,隐含层神经元个数依据经验公式(6)设置为15,输入输出延时阶次均设为2,权值及神经元偏置由rands函数随机给定,采用train函数对NARX网络进行训练。 图9 4种方法误差曲线 图9列出了采用4种不同方法辨识模型得到的4组验证样本输出参数ng、T4和T的最大相对误差均值。表2为4种不同方法建立涡轴发动机稳态辨识模型精度,由表可见输出参数ng、EGT和T的最大相对误差与最大相对误差均值。 表2 4种不同方法辨识模型精度 从图9和表2可知,PSO-NARX的不同验证样本最大相对误差及最大相对误差均值均小于PSO-BP、NARX和PSO-SVM。主要是因为PSO-NARX具有延时单元,将过去时刻的值反馈对当前时刻的输出产生影响,PSO对NARX网络的特征参数进行优化使得辨识模型的精度更高。BP神经网络是前馈神经网络无反馈单元,NARX网络具有反馈单元,但初始权值、偏置也是由随机函数产生,网络特征参数没有进行寻优。PSO-SVM精度也较好,但SVM对大规模训练样本会耗费大量的计算机内存和运算时间。由于PSO-NARX方法需要在最大迭代步数内对全部粒子进行适应度更新与寻优,PSO-NARX方法的训练时间也较长,但平均训练时间明显短于PSO-SVM方法。 1) 辨识模型输出参数ng、EGT和T的辨识结果很好的逼近了飞参数据实测值,证明了基于PSO-NARX网络的涡轴发动机稳态模型辨识方法的可行性。 2) 采用4组验证样本对辨识模型的性能进行验证,得到输出参数ng、EGT和T的最大相对误差分别为0.11%、0.26%和0.95%,最大相对误差均值分别为0.105%、0.193%和0.865%。表明了基于PSO-NARX网络的涡轴发动机稳态模型的精度达满足实际应用的精度要求。 3) 在相同的训练样本和验证样本情况下,本文采用的基于PSO-NARX网络的涡轴发动机稳态模型精度优于PSO-BP、NARX和PSO-SVM方法辨识的涡轴发动机稳态模型,有效的解决了涡轴发动机稳态模型建模复杂且精度不高的问题。 4) 若已知某些大气环境条件和该条件下燃烧室供油特性,即可通过辨识模型获取此大气环境下的发动机稳态性能,表明了基于PSO-NARX网络的涡轴发动机稳态辨识模型可用于其他任意大气环境下发动机稳态性能的递推估算。 5) 此辨识模型可用于后续在高原、高空及高低温环境条件下进行飞行试验的发动机状态的实时监控,为涡轴发动机控制规律的优化奠定基础,也为工厂对此型涡轴发动机试车试验提供相关支持。2 涡轴发动机稳态模型辨识方法
2.1 建立涡轴发动机稳态模型

2.2 基于PSO-NARX网络的稳态模型辨识方法
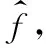
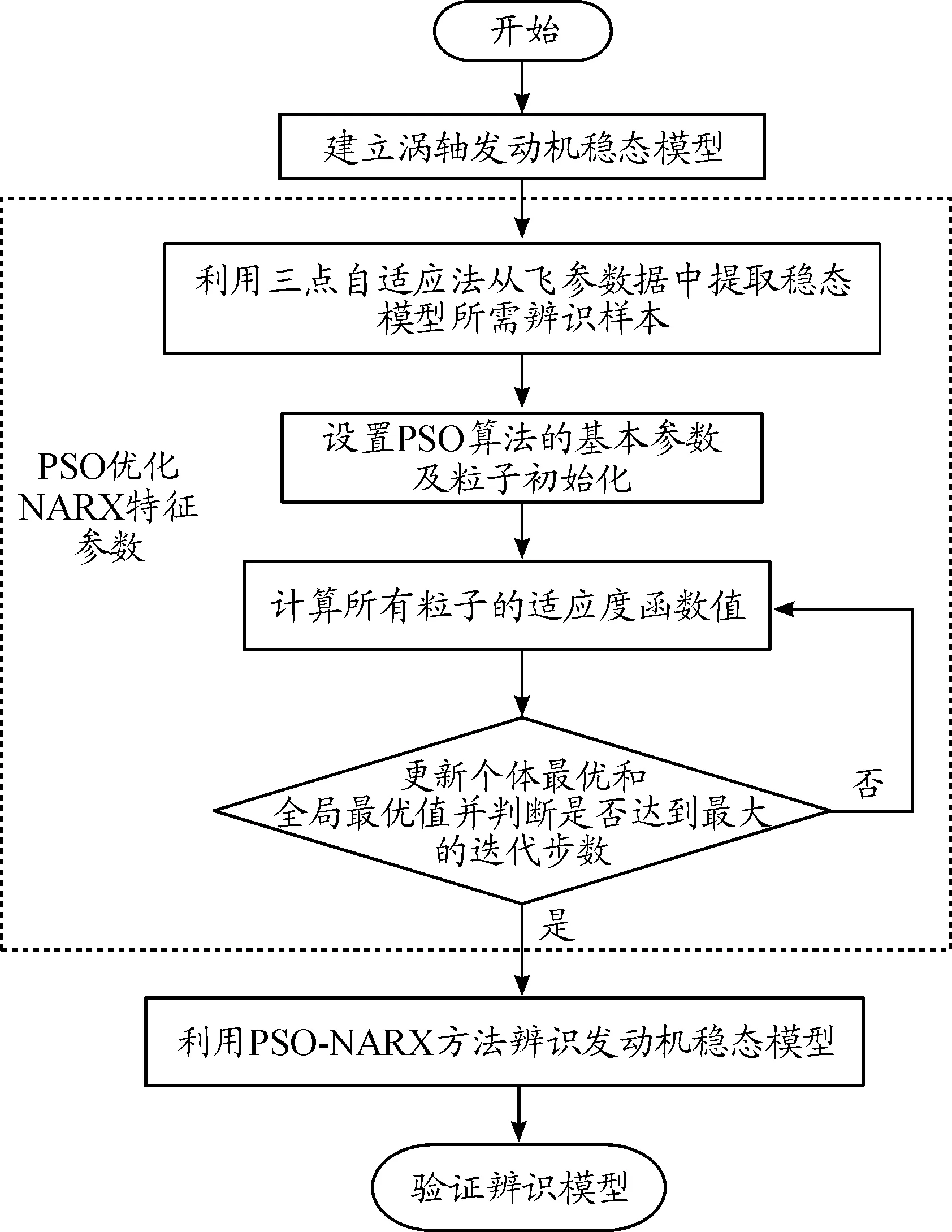
3 辨识过程与结果分析
3.1 从飞参数据中提取辨识样本与数据预处理
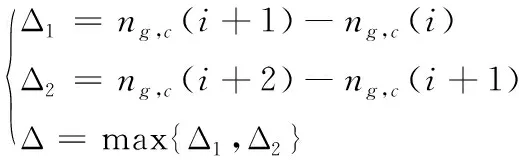
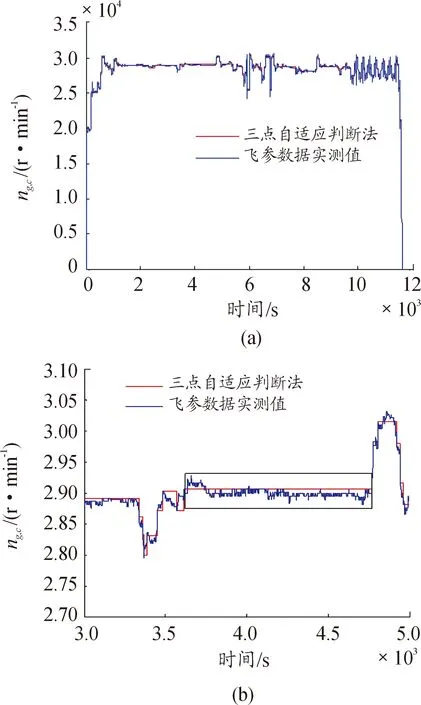
3.2 模型辨识结果


3.3 不同方法辨识效果对比

4 结论
