多航天器集中事件触发分组姿态协同控制
2021-05-06王帅磊周绍磊祁亚辉张瑞雪
王帅磊,周绍磊,祁亚辉,张瑞雪
(1.海军航空大学, 山东 烟台 264001; 2.中国兵器工业导航与控制技术研究所, 北京 100089)
对多航天器系统而言,姿态协同是正常作业的前提。通过控制系统内航天器的姿态,可以实现目标监控和定向通信等任务需求。现有研究从不同角度对该问题进行了分析。文献[1]设计了一种有限时间控制器,使多航天器系统能够在有限时间内达到姿态协同;文献[2]基于特殊正交群SO(3)提出了一种反步滑模控制方法;文献[3]对带有领导者的情况,提出了针对领导者姿态和角速度的滑模估计器;文献[4]进一步考虑了系统内存在多个领导者的情况,并以领导者的状态张成凸包,使跟随者的姿态都能收敛到这一凸包中。现有针对多航天器的研究大多都致力于使所有航天器的姿态和角速度收敛到同一个固定或时变值。
而对于某些复杂应用场景,需要将整个系统划分为若干个分组,每个分组内航天器都保持同一姿态,不同分组的航天器保持不同姿态。这种分组的情况称为分组姿态协同,并在SAR卫星监控[5]中有一定的应用需求。由于每颗卫星所处的位置不同,当多颗卫星同时对准一个目标,它们的姿态必然是有所差异的。将卫星编队划分为多个分组,并对每个分组内卫星的姿态进行调整,既能够实现对目标的全覆盖,又能解决因位置不同导致需要对每颗卫星单独设定姿态带来的困难和复杂度。在无人机编队飞行中,由于任务需求的变化,经常导致编队队形发生切换;同时,根据无人机的不同载荷,所执行的功能也有所不同。对无人机编队进行分组,既能够保持编队的整体性,又能够使编队完成复杂的任务。直接将整个编队分割为若干个孤立的子编队也能够实现同样的目的,但分割法将牺牲编队的整体性,由于多航天器系统采用无线通信,将通信链接断开后,重连将浪费一定的等待时间,并且存在重连失败的可能性;此外,分别控制孤立的子编队将导致控制变量和计算复杂度的增加,不利于编队的协同作业。
文献[6]考虑了基于无向图的多刚体系统,并将系统划分为两个分组进行研究,实现了二分组情况下的分组姿态协同,其缺陷在于仅适用系统包含两个分组的情况。文献[7]通过添加领导者的方法使跟随者达到分组姿态协同,但是需要针对领导者和跟随者分别设计控制输入,操作过程较为复杂。
考虑到系统内通信和计算资源是有限的,为了减少通信次数,针对一般情况下的多航天器姿态协同问题,研究人员已经展开了基于事件触发机制的研究[8,9]。而由于多航天器分组姿态协同问题提出时间较短,因此目前相关研究比较缺乏。
本文针对多航天器分组姿态协同控制问题,提出了基于集中事件触发机制的控制输入,使航天器之间仅在离散的时刻进行通信,从而减少通信次数。
1 多航天器系统构建
1.1 航天器姿态动力模型
考虑一个由N个航天器组成的系统,并将航天器标记为1,2,…,N。系统中的航天器可划分为s个分组,将这些分组标记为g1,g2,…,gs,并规定每个航天器仅能够被划分到唯一的分组。如果航天器i属于分组gj,那么定义映射Γ(i)=gj。在修正罗德里格斯参数的基础上,每个航天器的姿态动力模型可以表述为:

(1)
式(1)中:σi(t)∈R3、ωi(t)∈R3和ui(t)∈R3分别表示航天器的姿态、角速度和控制输入;正定对称矩阵J∈R3×3表示航天器的转动惯量;Gi(t)定义为:

(2)
式(2)中,
(3)
并且对任意一对向量x,y∈R3,有:

(4)
1.2 多航天器系统拓扑
将每个航天器视为节点,2个航天器之间的无向通信视作边,那么多航天器系统可以视为一个包含N个节点和若干条边的无向图,并可以通过邻接矩阵A∈RN×N和Laplacian矩阵L∈RN×N进行描述。如果航天器i和航天器j之间存在一条边,则aij=aji=1,否则aij=aji=0。在Laplacian矩阵L中,非对角线上的元素lij=-aij,对角线上的元素lii等于A中第i行所有元素之和。
由于本文中多航天器系统是分组的,因此基于现有关于分组一致的研究,本文采用如下假设。
假设1:任意2个分组之间满足入度平衡[10]。
假设2:矩阵L的非零特征值均为正实数。
本文还将用到如下引理和定义。
引理1 对于两个向量x∈Rn和y∈Rn,有:

(5)
引理2 对于向量x∈Rn和矩阵B∈Rn×n,有:
Bx||2≤B||Fx||2
(6)
式(6)中:·||2表示欧式范数; ·||F表示矩阵的Frobenius范数[11]。
定义1 称多航天器系统达到分组姿态协同,当且仅当同一分组中的航天器i和航天器j满足:
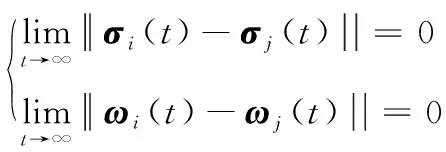
(7)
2 事件触发分组姿态协同控制
2.1 集中事件触发机制
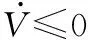
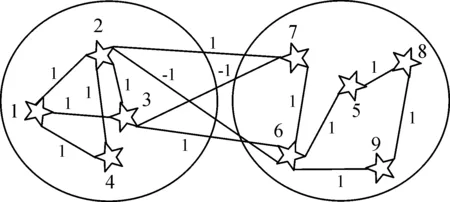
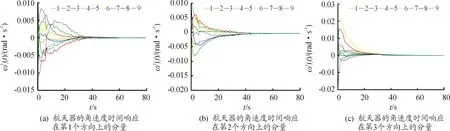
集中事件触发机制是指,对于多航天器系统,存在时间序列t0 为了便于表示,隐去变量中的时间符号(t),仅对触发时刻的变量保留(tk)。在分组情况下,设计控制输入的难点在于,既要能够使每个分组内航天器的姿态达到一致,又能够实现不同分组的自主区分。由于分组情况下系统邻接矩阵中的元素有-1存在,因此控制输入的形式与一般情况下姿态协同问题的控制输入不同。在集中事件触发机制下,对航天器i设计控制输入为: (8) 对多航天器系统设计整体触发函数为: (9) 式(9)中:G=diag(Gi);⊗表示Kronecker积。 (10) 因此 (11) 在此基础上,给出多航天器系统在集中式事件触发机制下的控制定理。 定理1 在集中事件触发机制下,给定航天器的控制输入ui(t)和整体触发函数f,若参数α和β满足: (12) 那么在控制输入的作用下,多航天器系统能够渐近达到分组姿态协同。 证明选定Lyapunov函数为: (13) 由于J是正定对称矩阵,L是半正定对称矩阵,因此显然Lyapunov函数V≥0。 对V求导,得到: (14) 由于Laplacian矩阵是对称矩阵,因此式(14)可以改写为: (15) 根据假设1,系统拓扑满足入度平衡,因此有: (16) 将式(16)代入控制输入式(8),得到: (17) 对控制输入式(17)进行化简,得到: (18) (19) βωTA⊗I3eω-βωTL⊗I3ω (20) α(Gω)TA⊗I3eσ+βωTA⊗I3eω≤βωTL⊗I3ω (21) 对式(21)左边取范数并对右边取绝对值,而对于一个标量值d,|d|=d||2。因此得到: α(Gω)TA⊗I3eσ||2+βωTA⊗I3eω||2≤ βωTL⊗I3ω||2 (22) 而根据引理1可知: (23) 因此结合式(22)和式(23)可知: (24) (25) 在任意一个触发时刻tk,总有eσ(tk)=eω(tk)=0,因此当式(9)成立时,能够保证: (26) M={(σ,ω)|ωTL⊗I3ω=0} (27) 定理1证明了在给定的控制输入作用下,多航天器系统能够达到分组姿态协同。下面对Zeno现象进行分析。Zeno现象是指,在有限的时间区间内发生无限次触发,即limtk+1-tk=0。如果系统内发生了Zeno现象,说明系统内航天器间的通信仍然是连续通信,无法达到节约通信和计算资源,减少通信次数的目的[8],基于事件触发机制设计的控制输入是无效的。因此,对于事件触发机制下的控制方法,分析Zeno现象的存在性并避免其产生是必要的。 定理2 在集中式事件触发机制下,给定航天器的控制输入ui(t)和整体触发函数f,在控制输入的作用下,系统不会发生Zeno现象。 证明根据事件触发机制的定义可知,在任意一次触发时刻tk都有f(tk)=0。在时间区间[tk,tk+1)内,对f求导可得: (28) (29) (30) (31) 式(31)表明相邻两次触发时刻之间的间隔有严格为正的下界,因此不会发生Zeno现象。证毕。 为了验证本文在集中事件触发机制下提出的控制输入的有效性,基于MATLAB平台,设计了包含9个航天器的系统进行仿真。航天器按顺序标记为1~9,并且1~4组成分组g1,5~9组成g2。本文中,所有航天器的运动特性都是相同的,因此假设转动惯量矩阵J∈R3×3为J=I3。多航天器系统构成的无向图如图1所示。 图1 多航天器系统构成的无向图 根据图2可以看出,在3个方向上,每个分组内航天器的姿态都收敛到一个常值,达到了协同;不同分组内航天器的协同姿态都不相同。航天器的角速度时间响应在3个方向上的分量如图3所示。 根据图3可以看出,系统内所有航天器的角速度最终都收敛到零,这表明随着t→∞,系统内任意一个航天器的姿态都不再发生变化,与图2中姿态时间响应收敛到常值是相吻合的。图2和图3表明系统能够达到分组姿态协同。 图2 航天器的姿态时间响应在3个方向上的分量曲线 图3 航天器的角速度时间响应在3个方向上的分量曲线 航天器运动过程中,触发时刻tk及触发时刻间隔tk+1-tk如图4所示。 图4 触发时刻及触发时刻间隔示意图 根据图4,在80 s的仿真过程中,系统共触发了90次,并且任意2次相邻的触发时刻之间的间隔最小值为min(tk+1-tk)=0.012>0。这表明系统不会发生Zeno现象,与定理2相符。 本文在事件触发机制基础上提出的控制输入仅需要90次通信就能够使系统达到分组姿态一致,而文献[6]中提出的控制输入需要航天器之间保持不间断通信,所占用的通信资源和消耗的能量更多,因此本文的控制输入更具优势。 在集中事件触发机制的基础上,本文针对多航天器设计了控制输入,使系统能够达到分组姿态一致,并且不会发生Zeno现象。仿真结果表明,相比基于连续通信的控制方法,本文设计的控制输入能够显著减少通信次数,节约通信资源。进一步研究将考虑引入分布式事件触发机制,使每个航天器能够独立计算并对触发函数进行判断。2.2 控制输入设计及稳定性分析
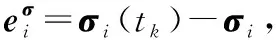
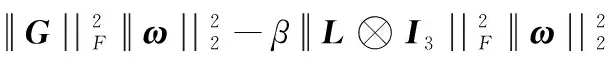







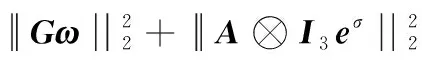

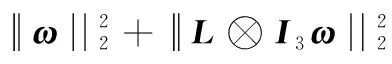
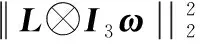



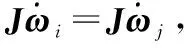





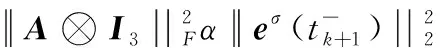
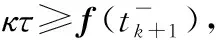
3 仿真结果与验证



4 结论
