基于Trot步态的液压四足机器人关节驱动力仿真分析

左鹏，吴浔炜，唐倩倩

（200082 上海市 上海理工大学 机械工程学院）

0 引言

机器人分为工业机器人和特种机器人，而特种机器人又包含服务机器人、军用机器人、娱乐机器人等，其中，军用机器人以双足式、四足式、六足式应用较多[1]。四足步行机器人机构简单灵活，承载能力强、稳定性好，在抢险救灾、探险、娱乐及军事等许多方面有很好的应用前景，其研制工作一直受到国内外的重视。

本文利用SolidWorks 软件建立液压四足机器人的三维模型，在MATLAB-Simulink 中搭建四足机器人对角步态运动框图，在ADAMS 中建立虚拟样机，通过MATLAB-ADAMS 联合仿真的方式实时模拟观测四足机器人在路面行走过程中的运动和状态，通过仿真结果对步态参数进行优化设计，在满足四足机器人稳定行走的工况下，使其关节驱动力对系统的影响最小。与其它步态相比，trot 步态具有较宽的速度变化，并且可在支撑相和摆动相之间平滑切换。行走时有较好的对称性，有效消除了机器人躯干的不平衡力矩，故使用trot 步态进行四足机器人仿真。

1 四足机器人结构

图1 所示为液压四足机器人三维模型。该机器人4 条腿采用相同结构[2]，整体尺寸为长1 000 mm，宽640 mm，高700 mm，自身质量约80 kg。

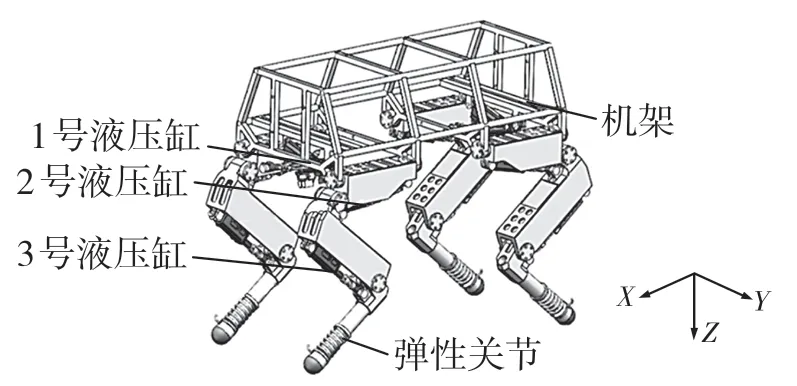
图1 液压四足机器人三维模型Fig.1 Three-dimensional model of hydraulic quadruped robot

采用前肘后膝式布置方式，每条腿有3 个自由度（髋关节一个主动自由度，大腿关节有一个主动自由度，小腿关节有一个主动自由度）。其中，1 号液压缸分别与机器人本体和髋关节相连，完成腿在YOZ 平面中的旋转运动，在受到侧向冲击和行走在凹凸不平整路面时，四足机器人可以通过控制1 号液压缸伸缩量与其他液压缸的协调运动来调整机器人的步态[3]，从而保持机器人稳定；2 号和3 号液压缸分别实现大腿和小腿关节在XOZ 平面内的转动，从而实现机器人腿的抬起和前进后退动作。小腿上装有一个被动弹簧机构，可以很大程度上缓解机器人脚落地时以及行走时地面对其的冲击，足端采用树脂材质的半球形结构，耐磨损，而且适应地形能力强。图2为机器人的单腿结构。

图2 液压四足机器人腿部三维图Fig.2 Three-dimensional drawing of a hydraulic quadruped robot’s legs

2 四足机器人单腿运动学建模

2.1 运动学正解

机器人正运动学用于在已知仿生机构各关节角度和连杆（腿长）长度的情况下确定机器人末端(足端)在空间中的具体位置。建立如图3 所示单腿D-H 坐标系[4]。图3 中：L1——髋关节的长度；L2——大腿关节长度；L3——小腿关节长度；θ1——髋关节角度；θ2——大腿关节角度；θ3——膝关节角度。相关连杆参数和关节变量[5]见表1。

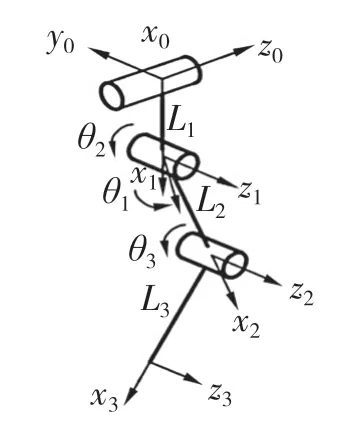
图3 单腿D-H 坐标图Fig.3 D-H coordinate diagram of single leg

表1 四足机器人单腿D-H 参数表Tab.1 Single-leg D-H parameters of quadruped robot

四足机器人的腿部为一个三连杆机构，通过笛卡尔坐标系的转换，根据D-H 坐标表示法，坐标系n 和坐标系n+1 之间的变换nTn+1（称为An+1）是4 个运动变换的乘积[6]，即：

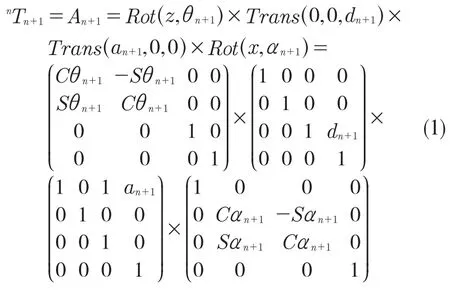
将表1 的数据带入到转换矩阵中，得出足端位姿相对于基坐标系的变换矩阵为

式 中：S1=sin（θ1），C1=cos（θ1），S2=sin（θ2），C2=cos（θ2）,S3=sin（θ3），C3=cos（θ3），S23=sin（θ2+θ3），C23=cos（θ2+θ3）。下文的推导过程也用这种方法表示。得出最终的变换矩阵为式（2），所以四足机器人的运动学正解为

2.2 运动学逆解

机器人的逆运动学就是通过机器人末端笛卡尔空间求解机器人关节空间，求机器人运动学逆解的方法有解析法和代数法、几何法、符号及数值方法、神经网络法等。本文中采用解析法[7]，对四足机器人正运动学方程进行反解可得出逆运动学方程，即根据足端坐标的关系式（3）求出关节角度，如下所示，式（4）代表的是前腿，后腿类似，注意正负号即可。

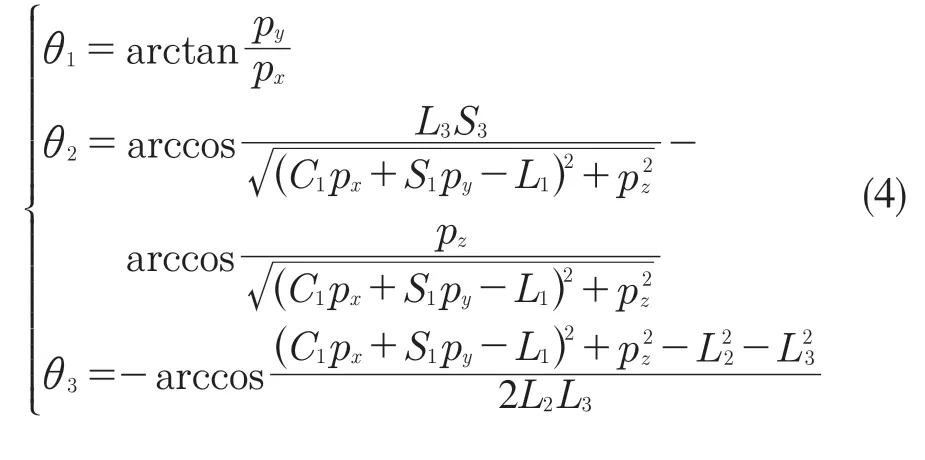
3 四足机器人液压缸驱动力分析

机器人在对角步态行走时，任意时刻只有2条腿与地面接触，其中，摆动相两条腿的液压缸驱动力此时较小，可以忽略不计。支撑相此时对角支撑，大小腿液压缸受力较大，故实际分析时，以支撑相大小腿液压缸驱动力为参考对象进行分析。假设不存在相对滑动这种情况，可视作机器人为一个五杆机构，如图4 所示。对此五杆机构做受力分析可以得出

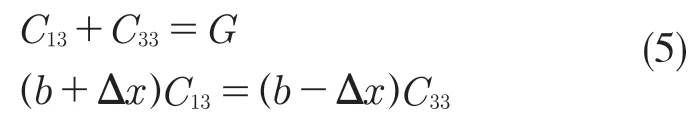
式中:G——机器人所受的重力，作用点集中于质心；C13，C33——前后支撑腿所受的地面支撑力；b——前后支撑腿机身方向距离的一半。

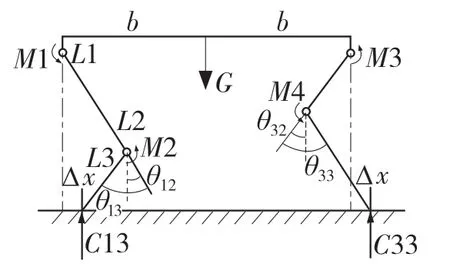
图4 四足机器人支撑相受力图Fig.4 Four-legged robot support phase force diagram

式（6）为前后腿髋关节和膝关节力矩平衡方程：

式中：θ12,θ13——前支撑腿的髋关节角度及膝关节角度；θ32,θ13——后支撑腿的髋关节角度及膝关节角度，可由前文的运动学逆解求得；L1，L2，L3——每条腿的三段连杆长度；Δx——2 个支撑足足端在坐标系中x 轴上的变化量，可用方程描述为

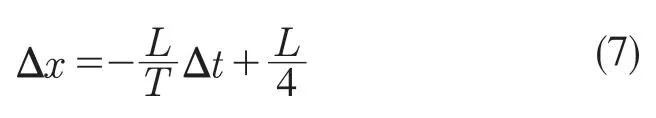
式中：L——步幅长度；T——步行周期；Δt——以当前支撑相为起点的步行时间。

参考图5 的单腿受力图，并将此多杆机构视为一个整体可得力与力矩之间的表达式：

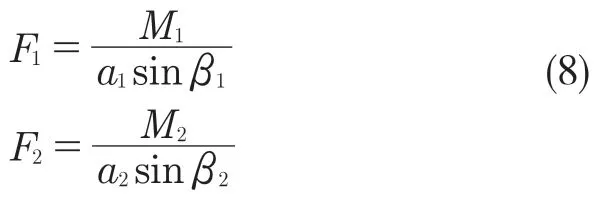
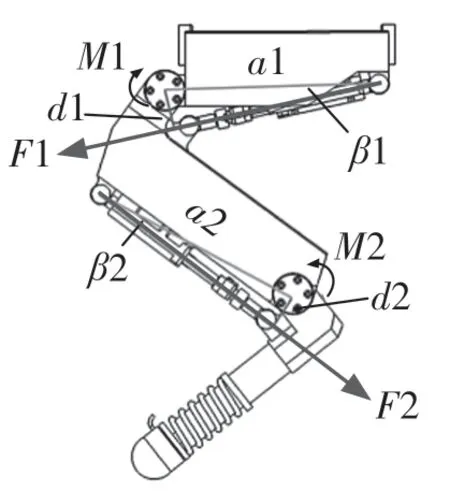
图5 四足机器人单腿受力图Fig.5 Four-legged robot single-leg force diagram

4 ADAMS 建模、MATLAB-simulink 框图搭建与联合仿真

4.1 ADAMS 建模及输入输出变量设置

在ADAMS 中进行四足机器人动力学仿真，需要将SolidWorks 的三维图以x_t 格式保存，然后导入到ADAMS 中，建立虚拟模型如图6 所示。在各关节设置转动副及移动副驱动，并设置好足端接触力，具体接触力参数[8]设置如图7 所示。

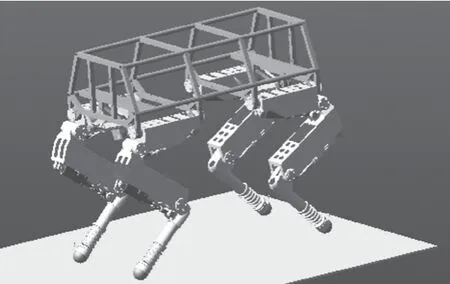
图6 机器人虚拟样机模型Fig.6 Robot virtual prototype model

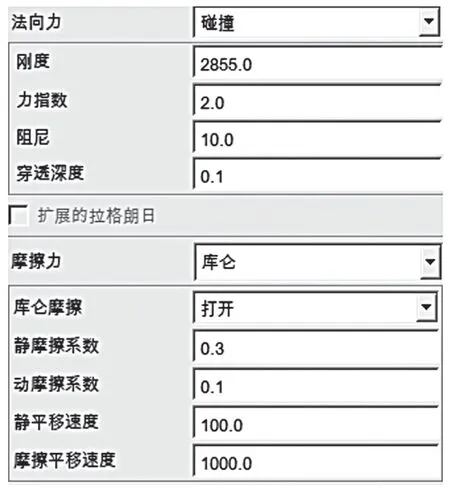
图7 接触力参数设置Fig.7 Contact force parameter setting

本文设计的液压四足机器人共有12 个自由度，由于在平整地面行走，不考虑侧向冲击，故髋关节自由度为0，实际共有8 个驱动，即每条腿的大小腿关节。输出为每个液压缸的实际驱动力，共8 个。利用Element 建立系统输入输出变量，定 义LF1，LF2，LF3，LB1，LB2，LB3，RF1，RF2，RF3，RB1，RB2，RB3 为各个关节的输入变量，利用VARVAL函数作为驱动的输入。定义LFyeya1，LFyeya2，RFyeya1，RFyeya2，LByeya1，LByeya2，RByeya1 和RByeya2 作为输出变量，LF1，LF2，LF3 分别代表左前腿髋关节、大腿、小腿液压缸伸长量，LFyeya1，LFyeya2 分别代表左前腿大小腿液压缸的实际驱动力。将虚拟模型的机械系统[9]导出，如图8 所示。

图8 输入输出设置窗口Fig.8 Input and output settings window

4.2 MATLAB-Simulink 框图搭建

Simulink 是MATLAB 中的一个模块图环境，用于多域仿真以及基于模型的设计，其中有现成的模块化Library，用户可以直接调取所需要的模块，进行框图的搭建，从而满足实际研究需要，方便快捷，省略了部分编程的需要，用户只需要简单了解MATLAB 的语言[10]，就可以搭建出想要的框图结构。如图9 所示为液压四足机器人Trot 步态Simulink 框图。

4.3 联合仿真平台搭建

为实现四足机器人稳定行走，需要实时对四足机器人状态进行分析和控制，ADAMS 和MATLAB 的联合仿真可实现这一过程。整个过程中，ADAMS 中虚拟样机作为被控制对象，需要从MATLAB 中获得驱动数据，即MATLAB 的输出为ADAMS 的输入；MATLAB 需要虚拟样机的实现状态调整控制程序，即ADAMS 中虚拟样机的状态输出为MATLAB 的输入[11]。如图10 所示。

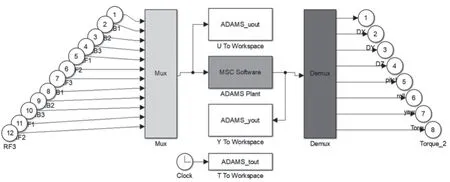
图10 四足机器人联合仿真平台搭建Fig.10 Four-legged robot joint simulation platform construction

5 运动仿真分析

运动仿真过程共持续5 s，由于本文研究的是通过调节运动参数来研究对液压驱动力的影响，故设计变量有3 个，分别是步长S，步高H以及运动周期T，通过调节单一变量的不同取值来分析运动结果，但由于实际工作量较大，故只针对左前腿进行分析，并且每个变量只取3 个不同数值来进行比较。如图11 和图12 所示分别为步高H 在30 mm，周期T 为1 s，步长S 在80，100，120 mm 情况下左前腿髋关节和膝关节液压缸驱动力曲线图。

图11 步长改变时髋关节液压缸驱动力Fig.11 Driving force of hip joint hydraulic cylinder when step length changes

图12 步长改变时膝关节液压缸驱动力Fig.12 Driving force of knee joint hydraulic cylinder when step length changes

通过曲线图可知，髋关节和膝关节液压缸驱动力在S 为80 mm 时波动较为平稳，突变点较少，没有太大的突变，而S 为100 mm 和120 mm 时，在足端着地时，液压缸驱动力波动较大，有较大的突变。故整体较合适的步长S 为80 mm。

图13 和图14 所示分别为步长S 在80 mm，周期T 为1 s，步高H 在30，40，50 mm 情况下，左前腿髋关节和膝关节液压缸驱动力曲线图。由图可知，髋关节和膝关节液压缸驱动力在步高H为40 mm时，波动较为平稳，幅值不会太大。而在H 为30 mm 和50 mm 时，波动点较多，而且幅值变化明显，会产生较大冲击，故整体较合适的步高H 为40 mm。

图13 步高改变时髋关节液压缸驱动力Fig.13 Driving force of hip joint hydraulic cylinder when step height changes

图14 步高改变时膝关节液压缸驱动力Fig.14 Driving force of knee joint hydraulic cylinder when step height changes

图15 和图16 所示分别为步长S 在80 mm，步高H 在40 mm，周期T 在1，2，3 s 情况下左前腿髋关节和膝关节液压缸驱动力曲线图。由图可知，髋关节和膝关节液压缸驱动力在周期T 为3 s 时，很平缓，几乎没有波动。而在T 为1 s 和2 s 时，驱动力较大，易产生冲击。故针对本文整体较合适的周期T 为3 s。

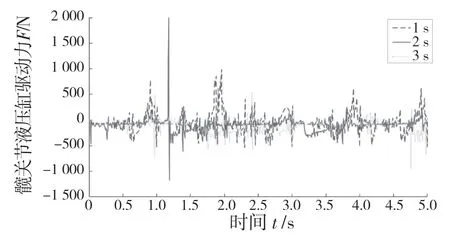
图15 周期改变时髋关节液压缸驱动力Fig.15 Driving force of hip joint hydraulic cylinder when cycle changes

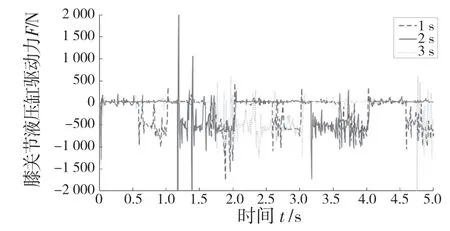
图16 周期改变时膝关节液压缸驱动力Fig.16 Driving force of knee joint hydraulic cylinder when cycle changes

6 结论

本文设计了一款液压四足机器人，通过建模与联合仿真，分析了平地Trot 步态下运动参数对四足机器人单腿的大小腿液压缸驱动力的影响，针对此实验，得出理想的运动参数为S=80 mm，H=40 mm，T=3 s，也验证了该结构的合理性，但实际运动参数视具体情况而定，如跨越障碍物及壕沟，加快速度时，也可修正运动参数满足需要，同时，也为四足机器人液压系统设计提供了参考。