基于LQR 与前向增益的无人车辆轨迹跟踪控制

彭传颂，赖杰，潘鲁彬

（1.200438 上海市 上海内燃机研究所；2.200438 上海市 上汽集团商用车技术中心）

0 引言

随着计算机科学技术的飞速发展，更多智能网联技术在无人车辆上得以应用，良好的控制算法是实现无人车轨迹跟踪和避障的前提[1]。目前主要的轨迹跟踪控制算法有纯追踪算法、模型预测控制算法以及线性二次型调节器LQR 控制算法等。纯追踪算法（Pure Pursuit）是一类前轮转向器路径跟踪算法，该控制算法的性能相当有限，仅限于车速相对较低的情况[2]。模型预测控制算法（Modle Prediction Control）适用于考虑约束条件的多输入多输出系统，具有良好的轨迹跟踪效果，但该算法较复杂且对硬件需求较严格[3]。LQR 控 制 器（Linear Quadratic Regulator）在平衡点附近对非线性系统近似线性化，以低能量损耗和快速的收敛速度为控制律设计基准，从而实现无人车辆的轨迹跟踪控制[4]。不同算法的控制效果可能会存在比较大的差异，收敛速度、能量消耗以及稳态误差等都会有所不同。本文首先基于车辆动力学模型进行状态观测器、LQR 控制器以及前向增益的设计，然后基于CarSim 与MATLAB/Simulink 联合仿真进行控制算法的测试验证。

1 无人车辆的模型建立

1.1 车辆运动学建模

车辆沿设定轨迹运动过程中，从t 时刻运动到t+Δt 时刻的速度大小和方向都会发生改变。图1 为车辆沿设定轨迹运动，则车辆在x 轴上的速度变化与纵、横向加速度如下：

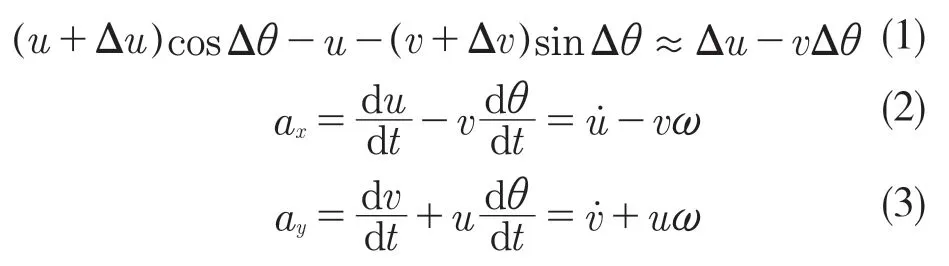
式中：u——车辆纵向速度；v——车辆横向速度；ω——车辆横摆角速度；Δθ——车辆质心运动速度方向变化；ax——车辆纵向加速度；ay——车辆横向加速度。

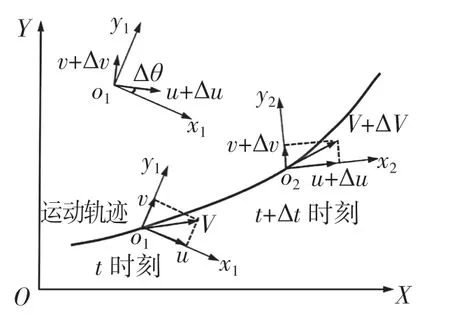
图1 车辆沿轨迹运动示意图Fig.1 Schematic diagram of vehicle motion along trajectory

如图2 所示，车辆实际运动过程中，根据车辆位置和期望轨迹的相对运动几何关系可得

式中：ρ——期望跟踪轨迹的道路曲率，当不计实际路径的影响时，无人驾驶汽车航向变化率为横摆角速度，即

图2 横向偏差与航向偏差示意图Fig.2 Schematic diagram of lateral deviation and heading deviation

1.2 车辆动力学建模

线性比例模型是一种典型的横向胎路摩擦模型，横向力被认为与轮胎侧偏角成线性的比例关系

式中：Fy——轮胎侧向力；Cα——轮胎侧偏刚度系数；α——轮胎侧偏角。

前轮的侧向速度为vf=v+aω，后轮的侧向车速为vr=v-bω。根据图3，得出了车辆前后轮胎侧偏角的大小关系为

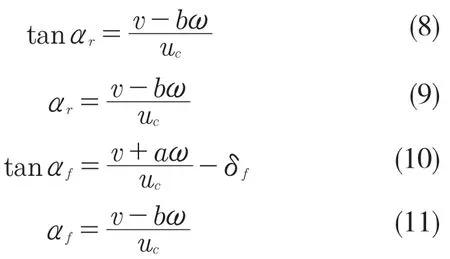
图3 车辆前后轮侧偏角示意图（以正值标出）Fig.3 Schematic diagram (marked with positive value)of front and rear wheel sides of vehicle

假定车辆速度恒定，则纵向运动可列为次要考虑的问题，根据质心运动定理和动量矩定理可建立车辆动力学模型如下：

2 轨迹跟踪控制器的设计

线性二次型调节器（Linear Quadratic Regulator，LQR）是一种基于线性状态空间方程的控制方法，以较低能量损耗和快速的收敛速度为控制律设计基准，实现车辆模型的反馈控制[5]。LQR 控制器设计也要首先假设所有系统状态都是已知的，控制器的最优性标准是使标量代价函数J 最小。

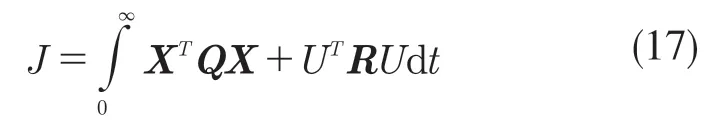
式中：X∈Rn——系统状态向量；U∈Rr——前轮偏角；Q∈Rn×n——状态权重矩阵；R∈Rr×r——输入权重矩阵。

由于高成本及其他原因，很多方法并不是直接测量出所有的车辆特征。例如，车辆控制中基本的轮胎侧偏角、航向角和横向速度，都很难直接测量得到，取而代之的是使用一些特殊观测器来重构需要的信息[6]。若偏移量ye可以被测量，则系统是可观测的。假设车辆为前轮转向且仅使用了前端传感器，则C=[0 0 0 1]；D=[0 0 0 0]T。可得车辆动力学模型的输出方程为式（18）以及状态观测方程为式（19）。

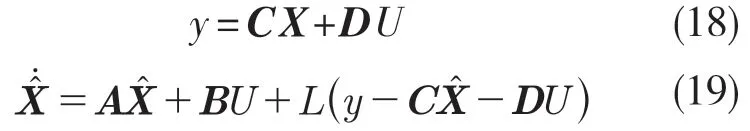
在没有建模误差的前提下，可进行前向增益N 的设计用以消除系统稳态误差：

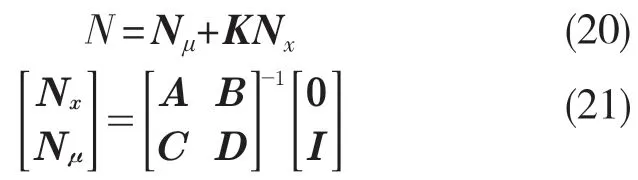
式中：K——根据LQR 控制算法所设计的控制器增益矩阵；Nx，Nμ——根据动力学模型确定；0——零矩阵；I——单位矩阵。

将车辆模型输入也附加到输出向量，构成增广设备输出向量，可将车辆动力学模型和观测器—控制器组成闭环的系统方程如下：

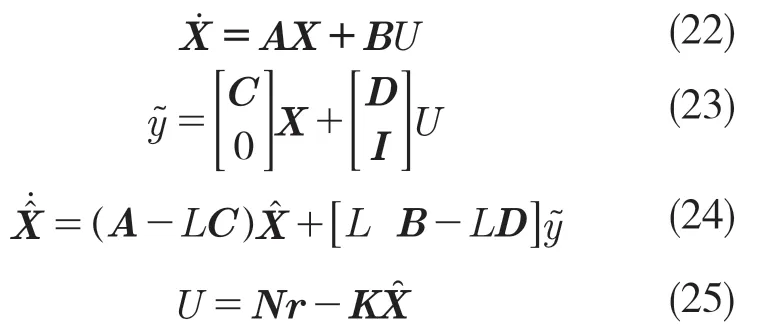
在控制器结构中引入积分环节，可用以降低系统的稳态误差，从输出中减去参考输入，对误差结果进行积分，则可得车辆的状态误差积分为式（26）。

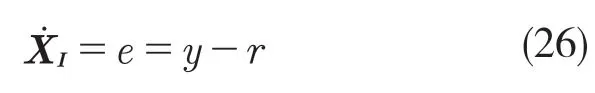
增加误差积分状态后的系统状态空间方程为

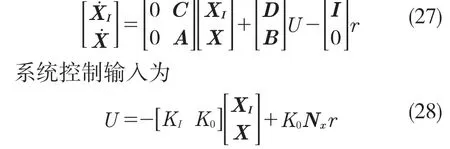
其中：K0——系统状态反馈增益；KI——误差积分增益。

3 基于CarSim 与MATLAB/Simulink 联合仿真验证

3.1 测试工况与标准

本文基于双移线工况对所设计的控制器进行仿真测试。如图4 所示，双移线工况由参考横向位置Yref和参考航向角ψref组成。

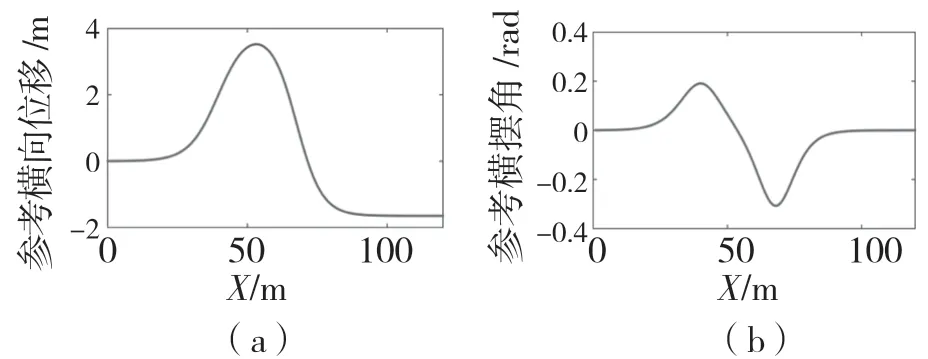
图4 双移线参考轨迹Fig.4 Reference trajectory of double shift lane

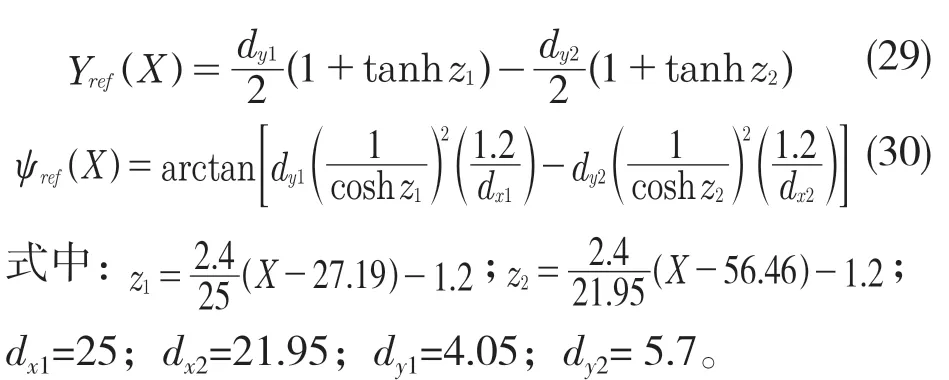
在车辆动力学模型中，轨迹跟踪控制器的设计规范通常由参考轨迹中的最大偏移量、最大前轮偏角和前轮偏角变化率给定。例如，典型无人车辆轨迹跟踪的基准要求如下[7]：

（1）前轮转角限制为‖δf‖≤40°；

（3）行驶车辆的横向偏差瞬态值不可以超过0.15 m，在稳态时不能超过0.02 m；

（4）侧向加速度不可以超过2 m/s2以保证乘客舒适性。极限约束为4 m/s2。

3.2 仿真结果分析

表1 列出了车辆动力学模型的参数值，其中，大部分参数为车辆的基本设计参数，但是有些参数则需要根据使用情况确定，如车辆行驶车速和装载质量等。

表1 车辆动力学模型参数值Tab.1 Parameters of vehicle dynamics model

选择不同的车速（10，20，30 m/s），将所设计的LQR 与前向增益控制器进行仿真分析，从而表明文中所设计的轨迹跟踪控制器具有良好的鲁棒性，且能达到期望的轨迹跟踪需求。

所设计的轨迹跟踪控制器仿真分析结果如图5 所示。由图5（a）可知，控制器对不同车速具有良好的鲁棒性，轨迹跟踪误差可以很快消除，且最大的稳态误差和瞬态误差均严格保持在允许范围内，具有良好的轨迹跟踪效果；由图5（b）可知，车辆航向同时也能很好地跟踪，但为了保证轨迹跟踪效果，随着车速的增大，航向跟踪效果有所下降；由图5（c）可知，当以很高的车速进行轨迹跟踪时，轮胎侧偏角满足在-5°≤Cα≤5°的范围内，仿真结果与建模假设不矛盾，满足小角度假设下的车辆动力学建模需求；由图5（d）可知，前轮偏角在约束范围内缓慢变化，满足前轮偏角的变化率需求，从而保证了执行机构的平稳运行；由图5（e）可知，车辆侧向加速度保证在规定约束范围内，保证了车辆行驶过程中乘客的乘坐舒适性。

图5 LQR 控制器与前向增益的仿真结果Fig.5 Simulation results of LQR and forward gain controller

4 结论

基于牛顿矢量力学体系进行车辆动力学建模，从而进行状态观测器、LQR 状态反馈控制器以及前向增益的设计，以实现无人车辆的轨迹跟踪控制。基于双移线工况进行控制系统的仿真验证，仿真结果表明：LQR 与前向增益控制器在车辆轨迹跟踪控制过程中具有良好的轨迹跟踪效果，对不同车速具有较好的鲁棒性。同时，在保证轨迹跟踪与航向跟踪的前提下，车辆具有良好的稳定性与舒适性。该控制算法可以满足无人车辆行驶过程中的轨迹跟踪需求。