简约深刻,螺旋上升
2021-05-04刘东升


摘要:针对在七年级上学期期中(末)复习阶段,很多数学教师选取大量数轴综合题进行备考训练,其中包含不少难度颇大的问题这一现象,根据数轴的有关内容是简约而深刻的,教学应该基于学情螺旋上升这样的理解,开设《数轴的再认识》专题复习课,重点引导学生打通绝对值的几何意义、数轴上两点之间的距离公式、线段的中点公式、定比分点公式等的联系,为解决“双动点”等综合问题做好铺垫;同时渗透数形结合、分类讨论、“序”等思想方法,帮助学生从“会解一道题”走向“学会解题”。
关键词:简约深刻;螺旋上升;《数轴的再认识》;专题复习课
在七年级上学期期中(末)复习阶段,很多数学教师会选取大量数轴综合题进行备考训练。其中有一类数轴上的“双动点”问题是近年来各个“名校”模拟考试或县区期中(末)考试中多见的考题,难度颇大,比如:
如图1,已知A、B、C是数轴上的三点,O为原点,点A表示的数为-12,点B表示的数为8,点C为线段AB的中点。点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时,点Q从点B出发,以每秒1个单位长度的速度沿数轴向左匀速运动;当P、Q相遇时,两点都停止运动。设运动时间为t(t>0)秒,则当t为何值时,P、Q、C三点中恰好有一点是以另外两点为端点的线段的三等分点。
题海战术常让优秀学生“空转”,而没有铺垫、难度较大的综合题常让一些适应性不好的学生疲于应付,没有因为大量训练而提高解题能力。
针对这一现象,笔者根据自己对数轴有关内容及其教学的理解,开设了一节《数轴的再认识》专题复习课。
一、教学内容思考
学生进入初中后,学习的数的范围首先扩充为有理数。为了研究有理数的相关概念及运算,人教版教材基于温度计,抽象出一个重要的工具:数轴。同时,给出了数轴的要素:原点、正方向和单位长度。指明了数轴的作用:实现数与形的一一对应,从而借助形直觀地表示数的问题,借助数精确地研究形的问题。实际上,数轴这个工具不但在定义相反数和绝对值、研究有理数的运算时有着不可替代的作用,而且能够用来比较有理数的大小、表示不等式(组)的解集。此外,数轴体现了解析几何的数形结合思想,可以升维推广为平面直角坐标系、空间直角坐标系,进而研究解析几何问题(包括函数图像问题),这对数学的发展起了重要作用。其中一个重要的问题就是两点关系和三点关系问题,具体表现为两点之间的距离和线段分点的表示。利用数轴可以得到两点之间的距离(坐标)公式,在此基础上可以得到线段中点、三等分点、四等分点……n等分点的(坐标)表示公式,这为高中学习平面解析几何(乃至空间解析几何)中的两点之间距离公式、线段定比分点公式做了重要铺垫。由上述分析可知,数轴的有关内容是简约而深刻的,即上手容易,但“联通八方”。
对于这样的教学内容,教学时要把握好“度”,特别是要注意在不同的阶段,基于学情,相机拓展,螺旋上升。具体来说,对于数轴的有关内容,在“有理数”一章新授课上,只要让学生掌握教材的要求,而不要急于拓展与提升;在“有理数”章末复习课上,可以对数轴及其相关概念(相反数、绝对值、有理数的运算、有理数的大小比较)做梳理,引导学生利用绝对值的几何意义,得出数轴上两点之间的距离公式;在“一元一次方程”一章学习等式的性质,且在“几何图形初步”一章引入线段中点的概念后,可以进一步组织学生利用数轴上两点之间的距离公式,得出线段的中点公式;而在七年级上学期期末复习阶段,可以整合数轴上线段的中点、三等分点、四等分点等,引导学生探究关联(七年级上学期的)有理数、整式加减、一元一次方程、几何图形初步等内容的综合题。
二、教学流程设计
(一)复习数轴及相关知识
问题1如图2,请同学们回顾数轴的定义及相关知识。
学生复述数轴的定义。教师强调数轴的三要素,然后引导学生回顾相关概念,比如相反数、绝对值,再如运用数轴理解有理数的大小比较、加减运算。由绝对值的几何意义,引导学生复习数轴上两点之间的距离公式,并进一步联想到中点公式。
(二)探究数轴上两个定点与一个动点的问题
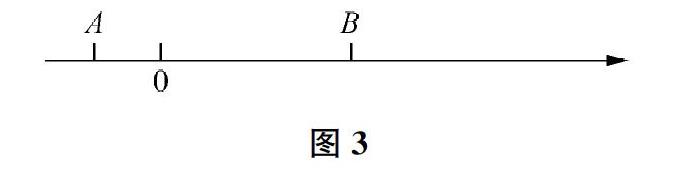
问题2如图3,数轴上已知两个确定的点A、B,对应着两个确定的数(请同学们假设出具体的值)。增设一个不确定的点M,对应着一个不确定的数m。
(1)当BM=6时,求m的值;
(2)当点M为AB的中点时,求m的值;
(3)当点M在线段AB上且AM=2BM时,求m的值;
(4)当AM=2BM时,求m的值。
让学生举例确定数轴上点A、B对应的两个数(比如-3、9),就是让学生参与设计例题或习题(提出问题),体现“学程重生成”的理念。在两个定点的基础上增加一个动点,四个问题的设计从距离公式的直接运用到中点公式的直接运用,再到三等分点公式的探究运用,最后到定比分点公式的讨论探究运用,解题层次(思考难度)逐渐增加——当然,学生有可能全部运用距离公式,通过解方程来解决。教学时,安排学生展示自己的解法,然后由教师点评、讲解。
(三)从特殊走向一般
问题3如图4,数轴上的点A、B分别对应着数a、b,且a+b>0,ab<0。另有点M对应着数m。
(1)当M为AB的中点时,用含a、b的式子表示m;
(2)设m=3,当M为AB的中点时,求代数式a+b+3的值;
(3)当AM=2BM时,用含a、b的式子表示m;
(4)当AM=3BM时,用含a、b的式子表示m;
(5)若点M到A的距离是点M到B的距离的k(k为正有理数)倍,试分析k的取值范围与点M的个数的关系。
出示题干后,先让学生确定原点的可能位置并说明理由,从而理解a+b>0且ab<0意味着a、b一正一负且正的绝对值大。然后,依次出示五个问题,让学生一般地探究(第2个问题是运用)中点公式、三等分点公式、四等分点公式,直至更一般的定比分点公式。作为最一般的情况,最后一个问题是教学的重点和难点,需要引导学生分类讨论:当0
(四)课堂小结,布置作业
问题4(1)本节课主要复习数轴及相关概念,你对哪个概念印象更深了?说说你的理解;
(2)本节课解题过程中涉及了一些数学思想方法,你积累了哪些?举例说说。
小结问题精准针对本节课的学习内容,而不是百搭式的“这节课你学到了什么”“这节课你还有什么困惑”等。
在学生回答,教师总结后,加大问题难度,布置课后作业。第一题是“若a-b+2=0,请思考|a+1|和|b-1|的关系”,让学生充分理解绝对值的几何意义和数轴上两点之间的距离公式的关系。第二题是文章开头给出的“双动点”问题,让学生尝试在距离公式和三等分点公式的帮助下,分类讨论解有取值范围限制的关于t的方程。
三、教学立意的进一步解读
数学教学的内容选取要以有利于学生深入理解数学知识、感悟数学思想作为标准,而不能只是满足于学生“细枝末节”的解题需求。因此,这节专题复习课还凸显了这样的教学立意。
(一)打通知识之间的联系
在这节专题复习课之前,学生通常已经知道绝对值的几何意义、数轴上两点之间的距离公式、线段的中点公式,但是,还没有打通它们之间的联系,也无法将它们适度推广并灵活运用。因此,出于基于学情螺旋上升的需要,这节课首先要帮助学生打通它们之间的联系:|a|的几何意义是数轴上表示a的点到原点的距离,而|a|=|a-0|,将其推向一般即可得到数轴上两点之间的距离公式;如图5,当AM=BM时,利用两点之间的距离公式可得m-a=b-m,变形可得m=a+b2,即得线段的中点公式。此外,要引导学生逐步推广线段的中点公式,得到线段的定比分点公式,为解决“双动点”等综合问题做好铺垫。
(二)注意思想方法的渗透
数轴习题的解答过程能体现很多数学思想方法,教学中要注意渗透。首先是数轴自带的数形结合思想(根据不同习题的解法特点,又可以细化为以形助数、以数驭形、数形互助)。渗透数形结合思想时,有一些细节值得说一说,比如,通常表示“形”的大写字母写在数轴上方,而对应的表示“数”的小写字母写在数轴下方。其次是字母表示数的不确定性蕴含的分类讨论思想。比如,当一个点对应的数没有明确的取值限制时,需要考虑该点在数轴上可能位于原点的左边、原点处或原点的右边;同样,当一个点到某个定点的距离确定后,需要考虑该点可能在定点的左边或定点的右边。这些是因为初中阶段研究的线段不是有向线段,并不带有方向(线段AB与BA是同一条线段)。最后是解决问题的“序”的思想。比如,先仔细读题,辨明已知的条件(起点),理解求解的目标(方向),再贯通解题的路径。而对于很多数轴综合题,贯通解题的路径时,一般要先明确数轴上点对应的数(有时要用含参数的式子表示),再结合线段之间的长度关系(点间的距离关系)列出方程,最后解方程(有时要视某个参数为主元)。经常这样开展解题教学,就能帮助学生从“会解一道题”走向“学会解题”。
参考文献:
[1] 郑毓信.“数学深度教学”十讲之七——“长时间思考”:反思与再认识[J].小学数学教师,2020(2).
[2] 刘东升.富有趣味:数学课堂教学的一种追求——以“平面直角坐标系”新授课教学为例[J].中学数学月刊,2020(7).
[3] 劉东升.我们需要怎样的“问题”驱动课堂——由美国莎维女士执教的函数图像课说起[J].教育研究与评论(课堂观察),2016(11).
[4] 刘东升.作业设计,功夫重在题外[N].江苏教育报,20180228.
