一种减小再入飞行器侧向气动非线性的布局优化方法
2021-05-04唐志共王文正
陈 功,唐志共,*,邓 晨,王文正
(1. 国防科技大学 空天科学学院,长沙 410073;2. 中国空气动力研究与发展中心,绵阳 621000)
0 引 言
升力式再入飞行器由于具有可重复使用、短时多次空天往返、任务载荷灵活、可实现水平着陆等优点,必将成为人类未来构建空天一体能力的重要平台。但与航空飞行器不同的是,升力式再入飞行器再入飞行速域大、飞行高度变化剧烈、飞行环境复杂,导致气动特性变化极大[1]。为满足采用单一布局形式的再入飞行器在整个再入阶段的飞行需求,必须对飞行器的气动布局进行精细优化,以满足不同飞行阶段的控制要求。实际中考虑到再入过程中的防热、容积率和配平等约束,升力式再入飞行器通常采用大钝头体、厚翼型和小展弦比的升力体布局。这种布局形式极易导致侧向气动力在跨声速段出现非常强烈的非线性特性[2],给飞行控制系统设计带来困难,严重影响再入飞行器的水平起降能力和飞行安全[3]。为解决这一问题,早在HL-20[4]研制过程中,气动工程师就采用了扭转体襟翼来消除舵面偏转对飞行器侧向气动特性的不利干扰。Lee[5]和Chaudhary[6]等在研究X-33和X-37两种飞行器的侧向非线性动力学特性的基础上,采用Weissman判据分析了飞行器的侧向稳定性。日本Jeong等[7]通过研究HYFLEX[8]飞行器布局参数改变引起的飞行器稳定性和操纵性的变化,分析了再入飞行器布局参数对控制性能的敏感性。国内唐伟[9-10]、周军[11]、王颖[12]等在分析高超声速飞行器布局参数变化对飞行器侧向气动特性影响的基础上,提出了减小侧向非线性的布局改进和减小操纵耦合的建议。
本文以解决实际工程中飞行器布局设计关键问题为目标,发展了一种以减小跨声速段侧向气动非线性的EGO布局优化设计方法。该方法以飞行器主要的气动敏感布局参数为优化对象,通过建立Kriging代理模型来替代传统的数值计算,实现对不同参数布局气动特性的快速预测,并可在优化过程中对代理模型进行自适应修正,可以提高布局优化效率。通过对一种升力式再入概念飞行器机翼布局的设计验证,优化后布局明显降低了飞行器在跨声速段的侧向气动非线性,满足了飞行控制系统的设计要求。
1 概念飞行器及侧向气动特性
1.1 概念飞行器基础布局
如图1所示,设计了一种常规布局形式的升力式再入飞行器为研究对象,进行气动力计算与侧向气动特性分析。该飞行器采用了钝头锥+细长外形机体的“混合机体”气动布局,机翼为兼顾高低速的小展弦比切尖双三角翼。为了提高升力,机腹设计接近于一块平板,机身两边也向后以一定曲率延展成为丰满横向截面。机体后部设计有大面积体襟翼,用于纵向配平。机翼后缘布置有襟副翼用于俯仰和滚转控制。机翼外侧末端加装了垂直尾翼,尾翼后缘有航向控制舵面。

图1 再入飞行器气动布局Fig. 1 Aerodynamic configuration of a typical reentry vehicle
1.2 基础布局气动特性计算
为获得再入飞行器跨声速段的气动特性,这里采用数值计算方法获得了飞行器的侧向气动数据。如图2所示,计算采用的是非结构混合网格,用三棱柱模拟附面层,四面体模拟空间流场同性区域,通过金字塔网格过渡三棱柱和四面体网格区域,总网格规模约为6百万。计算大气模型为理想气体模型,湍流模型取为SST湍流模型,解算器采用二阶迎风离散格式。

图2 数值计算非结构网格Fig. 2 Unstructured grid used for numerical simulations
横航向静稳定系数导数Clβ、Cnβ是飞行器控制系统设计时主要关心的侧向气动变化量。这里采用如下差分公式计算滚转和偏航力矩系数导数:

式中Clβ,3°、Cnβ,3°分 别表示侧滑 β= 3° 时计算得到的飞行器滚转和偏航力矩系数。
图3和图4给出了基准布局飞行器在跨声速段、不同飞行速度时的横航向静稳定系数导数的计算结果。由图中的计算结果可知,在跨声速区域再入飞行器基准布局的侧向静稳定系数导数随着迎角的增大,显示出明显的非线性。特别是滚转力矩系数导数在超声速(Ma =1.2)时与高亚声速(Ma =0.5)小迎角状态的极性相反。为分析造成以上侧向非线性的原因,图5给出了飞行器在Ma =0.9不同飞行状态时的压力云图:有侧滑时,在机翼和翼尖垂尾的共同作用下,在靠近垂尾的机翼外侧部分形成明显的非对称低压区,且随着迎角增大,低压区明显变化。从而导致飞行器侧向气动特性出现较大的非线性。

图3 偏航力矩导数变化曲线Fig. 3 Derivative of the yaw moment coefficient varies with the angle of attack

图4 滚转力矩导数变化曲线Fig. 4 Derivative of the roll moment coefficient varies with the angel of attack

图5 基准布局压力云图(Ma = 0.9,β = 3°)Fig. 5 Pressure contour of the baseline configuration(Ma = 0.9,β = 3°)
2 气动布局优化方法
2.1 布局优化变量
垂尾和机翼的干扰是导致再入飞行器基准布局侧向气动非线性的主要原因。因此,将小展弦比双三角机翼的内外侧的两个后掠角Φ1、Φ2以及垂直尾翼的后掠角Φ3作为布局优化参数(图6),以提高再入飞行器的侧向气动线性度为目标进行布局优化设计。

图6 布局优化参数Fig. 6 Schematics of the configuration optimization variables
2.2 布局优化目标函数
为在更大速度范围内提高飞行器的侧向气动特性,选择以下目标函数:
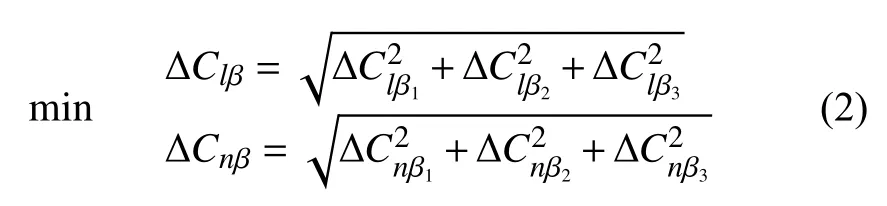
式中ΔClβi和ΔCnβi(i=1,2,3)分别是在Ma=0.5、0.9、1.2时由式(3)计算得到的力矩系数线性偏差量:

其中Aα+B和Cα+D分别是由三个迎角α1、α2、α3状态点处的Clβ和Cnβ采用最小二乘法拟合得到的线性函数。考虑到跨声速段已经接近再入飞行器的飞行末段,飞行器的实际飞行迎角较小,因此将三个计算的迎角样本点设计为α1= 0°、α2= 5°、α3= 10°。为计算目标函数,一种布局样本就需要计算如表1所示的18个飞行状态,这对于常规的Navier-Stokes计算代价很大。为减少计算资源消耗,提高设计效率,这里采用一种基于Kriging代理模型的自适应优化方法对飞行器布局进行优化。

表1 单样本目标函数计算状态Table 1 Simulation parameters for the calculation of one sample’s objective function
2.3 布局优化方法
多目标优化要求全局优化算法具有目标函数估值次数少的特点[13]。在飞行器气动布局设计时,由于飞行器典型特征点的气动数据计算时长较多导致这个矛盾非常突出[14]。基于Kriging代理模型的自适应迭代优化方法由于同时考虑模型预测值和预测方差来指导生成新的样本,能够大幅提高模型的最优逼近精度,并可以大大减小目标函数的估值次数。这里采用具有最大期望改善(Expected Improvement,EI)迭代准则的EGO优化方法完成对再入飞行器布局的优化设计[15]。
EI是指在一个给定特征点的响应值目标改进的概率。作为优化搜索的质量因素,来权衡局部搜索和全局搜索。设点x出的预测值为,标准差为s,预测结果满足标准分布,则可以给出EI的公式为:

其中fmin=min(y1,···,yn),φ和φ分别表示标准正态分布函数和正态分布密度函数。上式兼顾了搜索位置处的目标预测值和预测值误差:当预测误差很大时,s就很大,引导EGO算法向预测误差大的位置搜索;当目标预测误差小时,值就很大,引导EGO算法向极小值附近搜索。因此,EGO算法通过在EI值最大处增加迭代点,来兼顾全局性和收敛性[16]。对于优化过程中的约束:

可以转化为概率函数:


这里采用遗传算法求解EGO模型的EI值,建立再入飞行器布局优化的流程如图7所示。

图7 布局优化方法流程Fig. 7 Flowchart of the aerodynamic configuration optimization process
3 气动布局优化结果及分析
规定再入飞行器机翼的待优化布局参数的变化范围如下:

由拉丁方试验设计方法在以上三个待优化参数构成的三维参数空间内确定12个初始布局样本点。图8给出了不同布局样本在设计空间内的分布,布局样本较为均匀的分布在三维设计空间,并取中间样本作为基准布局。

图8 优化布局样本分布Fig. 8 A scatter plot of samples for the optimization configuration
采用与上节相同的N-S解算器,分别计算所有样本的侧向气动特性,获得每个布局样本由式(2)计算的优化目标函数值,建立飞行器布局优化参数和侧向气动线性度偏差的预测代理模型。并考虑以下升阻比约束:

经过两轮迭代优化,分别得到优化布局Opt1和Opt2。图9给出了上述两种优化布局由式(2)和式(3)计算得到的侧向力矩系数线性偏差量。

图9 优化布局侧向力矩系数线性偏差Fig. 9 Linear deviation of the lateral moment for optimized configurations
图10和图11分别给出了Opt1布局和Opt2布局的横航向静稳定力矩系数导数与基准布局的对比结果。表2分别给出了Ma =0.9时,基准布局、Opt1布局和Opt2布局的机翼布局参数和升阻比结果。
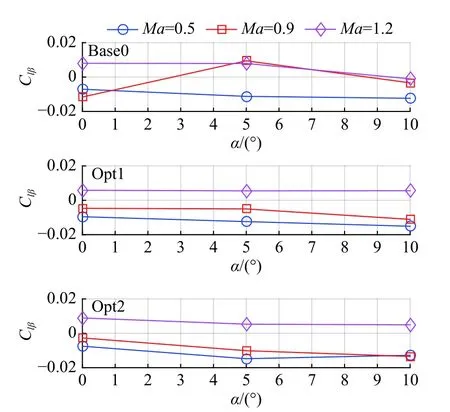
图10 布局滚转力矩系数导数Fig. 10 Derivative of the roll moment coefficient
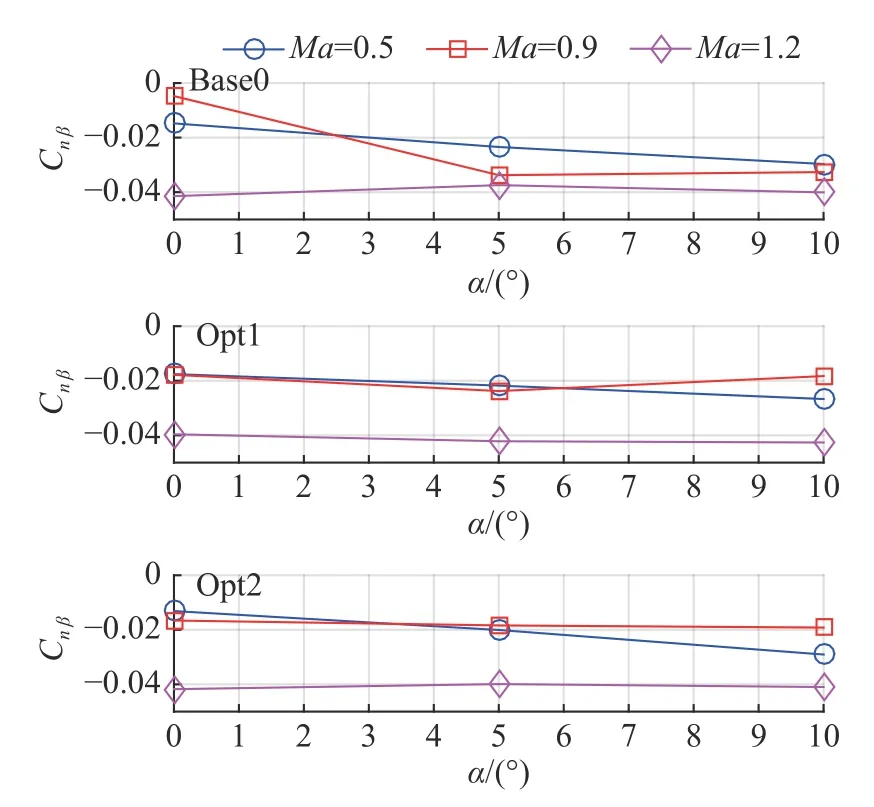
图11 偏航力矩系数导数Fig. 11 Derivative of the yaw moment coefficient
由上述计算结果可知,Opt1布局与Opt2布局的侧向气动线性度相较基准布局明显提升。由Opt1布局参数的优化结果可知,增大内侧机翼后掠角、减小外段机翼后掠角和垂直尾翼后掠角可以明显提高再入飞行器在跨声速段的侧向气动线性度,但飞行器的升阻比会略有下降。为此,Opt2布局减小内侧翼后掠角、增大外翼和垂尾后掠角,同时兼顾了侧向气动线性度和升阻比要求。
图12给出了Opt2布局Ma= 0.9、β= 3°时的压力云图。对比图5和图12,可知优化后布局随着迎角增大,在靠近垂尾的机翼外侧仍会出现不对称的低压区。但相较基准布局,左右机翼低压区范围的不对称性明显减弱,从而增加了飞行器侧向气动特性的线性度,提高了飞行器的可控性。

表2 布局优化结果Table 2 Aerodynamic configuration optimization results
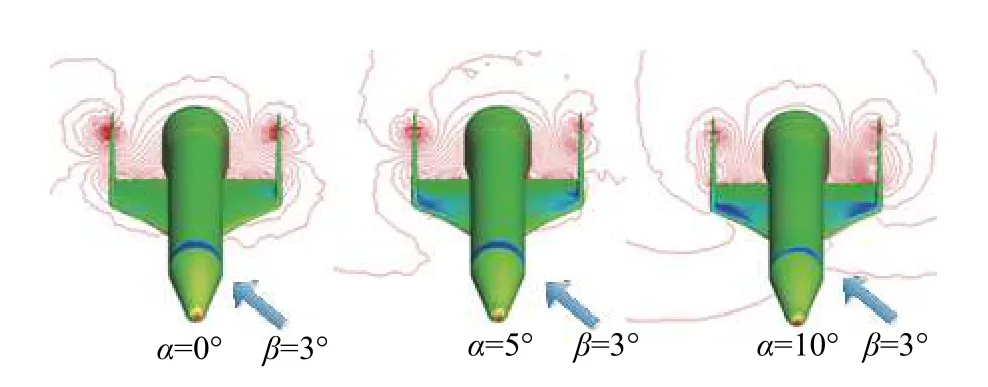
图12 Opt2布局压力云图(Ma = 0.9,β = 3°)Fig. 12 Pressure contour for the configuration Opt2(Ma = 0.9,β = 3°)
4 结 论
本文主要针对升力式再入飞行器跨声速段侧向气动非线性的问题,发展了一种基于Kriging代理模型的自适应布局优化设计方法。通过对一种概念飞行器的机翼布局参数的优化结果表明,优化后布局可以明显降低飞行器在跨声速段的气动非线性,同时满足升阻比约束,证明了所发展的方法是基本可行和有效的。为进一步提高再入飞行器布局设计水平,未来可进一步研究建立气动布局参数到控制性能要求的关联模型和评估准则,提高气动布局满足控制性能要求的水平,实现气动与控制的一体化快速设计,实现飞行器综合性能优化。
