基于APSE确定高超声速边界层第二模态中性曲线下支

谷晓培，刘建新

(天津大学 力学系，天津 300072)

0 引 言

从较大型民用客机的发展到高超声速飞行器的研制过程中，人们发现层流边界层和湍流边界层的热传导系数和所产生的摩擦阻力相差很多。正确预测转捩位置对飞行器的设计具有重要的意义。通过前人对转捩问题的研究，一般认为，转捩是由流动中的扰动失稳导致的，主要可以分为三个具有不同特征的阶段：感受阶段、层流中扰动的演化阶段、以及转捩阶段[1-2]。而感受性阶段作为转捩过程的第一个阶段，决定了引起转捩的不稳定波的初始条件，包括频率、幅值和相位。因此，要从科学意义上研究清楚转捩过程，准确预测转捩位置，边界层的感受性是关键的一个环节。除了感受性阶段，线性稳定性阶段作为转捩过程中相对尺度最长的阶段也格外重要。在工程中可以使用eN方法来估计转捩位置就是利用了线性稳定性的这一特征。

已有研究[3]表明，在超声速边界层中存在着多个不稳定特征模态，如Mack第一、第二模态。不同的模态之间可能相互转化，而且有些模态的相速度接近于来流速度或者来流中声波的传播速度，这意味着这些模态可能与来流中涡波、熵波和声波有紧密的联系，因此超声速边界层的感受性问题比较复杂。其中Fedorov等[4-6]研究了超声速边界层对来流中快、慢声波的感受性，提出了“同步”的概念来解释高超声速边界层中的感受性过程。Fedorov和Khokhlov将边界层前缘的离散模态分为快模态和慢模态。根据边界层前缘感受性理论，来流中的快、慢声波可以分别激发快、慢模态。他们对无黏稳定性进行分析时发现，第二模态波的产生与快、慢模态的同步点有关。即在某些条件下，当快、慢模态发展到下游的某一位置，可能会具有相同的相速度，这个位置即为“同步点”。因为表征快速变化的波数实部相同，而波数的虚部αi＜＜1，两个模态由于基本流的弱平行效应耦合起来，从而导致模态转化。这就意味着在流场中需要同时存在快、慢模态。事实上，即便入口只引入一个模态的扰动也可以依靠非平行性激发出第二模态。从物理上来讲，一个模态在非平行流中传播时，其形状函数会偏离局部特征函数，由此产生的畸变会在另一个模态的特征函数上的投影一般不为零，这样的散射效应会将一个模态的部分能量转化到另一个模态。因此，Mack第二模态的激发实际上是上游快、慢模态共同作用的结果，单一地考虑其中一个模态无法正确地刻画Mack第二模态的生成。

在工程中，通常使用基于线性稳定性理论即eN方法来进行转捩预测[7]，即通过计算不稳定波的线性增长倍数来预测转捩。使用这一方法时，需要确定积分式的起始位置坐标x0。经典的eN方法只计算扰动的增长而不考虑扰动的衰减。因此积分起始位置就是扰动增长开始的位置。在一个二维流场中，给定一个展向波数β，则在频率和流向坐标x所组成的面内可以找到一条中性曲线。曲线上的每一个点对应于某一频率的扰动，其积分的起始位置就是与该频率对应的中性曲线下支的位置。

因此，综合高超声速边界层中的感受性过程和传统的eN转捩预测方法，在研究问题中需要考虑以下两点：第一点，流场的非平行性特征。在高超声速边界层中，流动具有非平行性，而在使用线性流动稳定性理论（LST）的方法[8]来研究稳定性时，一般需要做平行流假设，即假设边界层厚度不变，将小扰动设成行进波的形式来进行计算。这在大雷诺数的情况下，带来的误差并不大，但是在当地雷诺数较小的区域，平行性假设会引入较大的误差。第二点，快模态、慢模态的感受性机制。即快、慢模态所激发出的第二模态可能受感受性机制的细节差别导致中性曲线下支存在差异，由此会影响到eN积分中积分起始点即中性曲线下支的确定。

为研究以上问题，本文将在考虑流场的非平行性前提下，利用线性抛物化稳定性方程（LPSE）方法及其伴随方法开展研究，以期在考虑感受性过程的前提下对Mack模态中性曲线下支的确定问题进行探讨，并在此基础上给出确定中性曲线下支的方法。

1 马赫数4.5工况下考虑平板边界层感受性的中性曲线下支研究

为了研究考虑感受性的中性曲线下支确定问题，本节以Ma= 4.5的可压缩平板边界层为研究对象，以Blasius相似性解为基本流，以入口处边界层动量厚度为无量纲长度，采用线化N-S方程（LNS）和线性抛物化稳定性方程（LPSE）方法分别对边界层内快、慢模态激发第二模态不稳定波的过程进行研究。首先计算出离散模态扰动的演化过程，然后通过对结果的处理，得到中性曲线的下支。计算参数表1所示。这里采用了两种不同的数值模拟方法—LNS方程和LPSE方程。其中对于本文所研究的小扰动问题来说，LNS方程[9]可以完全替代N-S方程，并且求解效率也要高很多。因此本文选用LNS方程的结果作为基本参照对象，更多的相关LNS方程的推导以及验证可以参考文献[9]。下一小节主要就LPSE方程加以介绍。

表1 算例1的主要计算参数Table 1 Main calculation parameters of Case 1

1.1 线性抛物化稳定性方程

线化抛物线稳定性方程（LPSE）是一种有效的描述小扰动线性演化的方法[10]。这种方法由于可以考虑边界层的非平行效应，因此计算较为精确。同时，对于小扰动问题来说，其对扰动演化的预测与N-S方程一致，但具有更高的效率，其系数矩阵元素的具体表达式见周恒等的著作。

考虑可压缩边界层，从有量纲的完全N-S方程出发，选取适当的特征量将其进行无量纲化，可以得到无量纲的N-S方程。

将方程中的瞬时量设为定常基本流与扰动量的和：

对于空间模式来说，由于边界层厚度沿流向是缓慢变化的，基本流沿流向也是缓变的。因此，T-S波的形状函数和流向波数也是沿流向缓变的。假设展向波数不变，则扰动可以写成下列形式：

将式（3）代入到线性扰动方程，去掉方程中二阶以上小量，将其抛物化，即可得到线性抛物化稳定性方程（LPSE）：

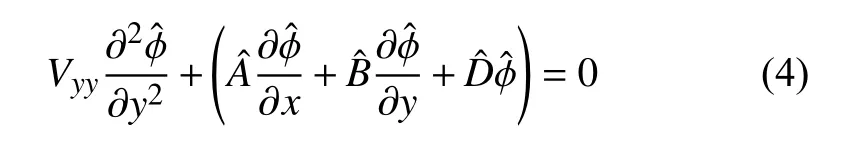
壁面处使用无滑移边界条件和适当的温度条件，使用等温条件时为：

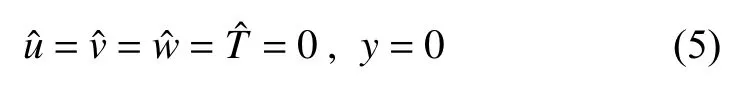
使用绝热条件时为：

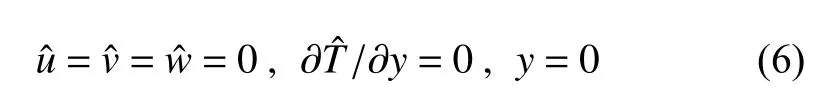
边界层外的自由流条件为：

在进行LPSE的具体求解时，方程（4）中有两个未知函数，即形状函数和波数α，一个方程不足以解两个量，所以需要补充一个条件。本文选用式（8）作为补充条件，其物理意义是形状函数代表的扰动动能沿流向不变。在实际应用式（8）作为补充条件时，需要对波数α进行迭代求解，即用式（9）计算出一个新的流向波数αnew，判断新旧流向波数之间是否满足预设精度，若不满足，则将αnew代回方程（4）中求出新的解，如此反复迭代，直至预设精度满足补充条件为止。

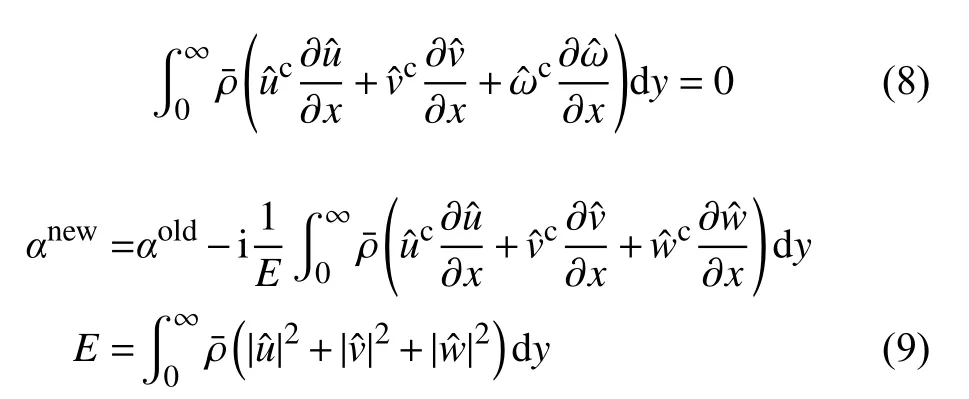
其中，E为扰动能量；上标“c”表示复共轭。

由以上推导可知，LPSE方程给出的解实际上对应于式（3）中的形函数以及相位函数。二者共同构成了边界层内迭代求扰动的演化过程。LPSE并没有直接给出扰动的增长率。因此，还需要给出求解增长率的方法。这里我们注意到，考虑到流场的非平行性，此时增长率αe在定义的过程中需要包括流向波数以及形函数沿流向变化的部分[11]，即：

1.2 离散模态的小扰动演化的LPSE模拟

在计算问题之前，首先针对Case1计算其线性稳定性特征，给出其离散模态的基本情况。图1和图2分别给出了Case1条件下用线性稳定性理论（LST）计算得到的快、慢模态的增长率和相速度的实部沿流向的变化。从图中可以看出，在中性曲线的上游，快模态和慢模态都是衰减的。相比而言，快模态的衰减率更小一点。流场此时主要是快模态主导流场中的离散模态。在下游约x= 200位置处，快、慢模态的相速度接近。该位置为同步点，同步点之后慢模态连接的是一个增长很快的第二模态，而快模态对应为一个稳定的模态。然而，这里有必要指出的是，LST所给出的结果对应的实际上是特征值问题的解，即特征值和特征函数。这也就意味着，这一结果既没有考虑流场的非平行特征，也无法计算流场中两个模态同时存在的情况。

图1 Case 1由LST给出的快、慢模态增长率沿流向分布Fig. 1 Growth rate distribution along the flow direction given by LST for the fast and slow modes in Case 1

图2 Case 1由LST给出的快、慢模态相速度沿流向分布Fig. 2 Phase velocity distribution along the flow direction given by LST for the fast and slow modes in Case 1

虽然以上给出了线性稳定性分析的结果，然而依照Fedorov的理论，流场中Mack第二模态的激发过程实际上依赖于流场的非平行性，以及两个离散模态同时存在并且共同作用的结果。为此，分别用线性抛物化稳定性方程（LPSE）以及线化N-S方程（LNS）来计算离散模态扰动的演化，进而确定其中性曲线下支的位置。

在具体计算时，选取上游某一位置的LST的离散模态（即快模态或者慢模态）作为初值。具体的入口扰动参数如表2所示。

表2 case1的入口扰动参数Table 2 Entrance disturbance parameters in Case 1

图3给出了分别用LNS和LPSE方法所计算出来的预测结果。可以看出，不管入口为慢模态还是快模态时，两种方法给出的扰动演化过程基本相同。不管入口给快模态还是慢模态，扰动的增长率都有一个波动过程，这主要是由于在流场的下游位置慢模态占主导地位，而在流场的上游位置是快模态占主导地位。因此在上游的位置，首先存在着一个慢模态到快模态的模态动态切换过程，但是随着扰动逐渐向下游演化，下游流场又由慢模态所主导，因此在流场的更下游主要体现还是慢模态的扰动，快模态的幅值越来越小，慢模态的幅值越来越大，进而激发第二模态的不稳定波，而主导了下游的不稳定波模态。换句话说，流场中此时存在着主导模态切换的过程，所谓波动现象其实对应的是流场主导模态的切换。这一特征在LPSE和LNS的计算结果中都可以观察得到。

图3 Case 1中不同方法给出的扰动波增长率沿流向分布的比较Fig. 3 Comparison of the growth rate distributions along the flow direction given by different methods in Case 1

这也就意味着这两种方法不同于LST方法，是可以同时计算两个离散模态的演化的。同时还可以注意到，LPSE和LNS方法给出的Mack模态中性曲线下支位置大致相同，都大约在x= 210的位置处。这也就意味着，对于本文所研究的问题来说，使用LPSE可以得到与N-S方程同样的结论，但效率更高。因此，以下的研究中主要使用LPSE来计算离散模态扰动的演化过程以保证更高的效率。

从图3中还可以看到，在上游某一位置分别选取慢模态和快模态的解为初值，计算所得到的中性点的位置存在较大差异。其中快模态演化过程中对应的下中性点位置在x= 250；而慢模态演化过程中对应的中性点位置在x= 210。也就是说随着在入口处给定不同的离散模态，中性曲线下支的位置是有明显差异的。考虑到对于一个实际问题，流场中什么样的扰动都存在。此时，结合中性曲线的定义，选取更靠前的中性位置作为中性曲线的下支界，也就是说，此时应该选取x= 210作为该问题的中性曲线下支。在此位置之前，不管什么样的扰动，都是衰减的。

正因如此，可以得到使用LPSE来确定考虑感受性的中性曲线下支确定方法。首先，使用LST计算出衰减区域内快模态和慢模态两个离散模态；然后，使用LPSE分别计算两个离散模态向下游的演化过程进而确定各自的中性点。最后，比较这两个中性点，取更靠近上游的位置作为中性曲线的下支。

通过以上的方法来计算中性曲线下支是可行的。但是这种方法有一些地方值得商榷。第一，使用LPSE来计算离散模态的演化需要事先使用LST来计算出衰减区内的两个离散模态作为入口边界条件。然而，由于衰减区域存在着主要由边界层外流动影响的连续谱的近中性解，因此无法直接使用幂法来迭代计算衰减的离散模态。一种常见的方法是使用迭代法从Mack模态的增长区逐渐改变参数从而计算出上游衰减区中的两个离散模态，如图1。但是这样意味着相对比较繁复的寻找衰减区离散模态的过程。换句话说，该方法的操作性比较复杂，入口边界条件不好给定。第二，在LPSE分别计算离散模态演化以确定中性曲线下支的过程中，实际上是进行了两次LPSE的演化计算。由于事先并不知道到底是慢模态还是快模态的演化可以得到相对位置更靠近上游的中性曲线下支，因此两个离散模态的演化过程都需要进行计算。如果有这样的方法可以一次性的来确定中性曲线下支，那么其效率应该更高。

基于以上所提到的计算中性曲线方法存在的不足，本文提出了一种结合线性抛物化稳定性方程（LPSE）及其伴随（APSE）的方法来计算非平行边界层稳定性，并以此确定考虑感受性的中性曲线下支的位置的方法。该方法有助于解决前面所提到的非平行效应和模态同步这两大难点的同时，还具有高效和易操作的特点。

2 基于伴随抛物化稳定性方程确定中性曲线下支

正如前文所述，基于LPSE来确定中性曲线下支的方法有其待改进之处。注意到伴随方程与原线性方程相比，具有特征值互为共轭关系的性质。利用该性质，就可以基于伴随抛物化稳定性方程（APSE）来确定考虑感受性的中性曲线下支。该方法可以有效改善基于LPSE方法的不足。以下将对该方法进行介绍，并利用该方法来确定不同工况下的中性曲线下支界的位置。

2.1 伴随抛物化稳定性方程（APSE）的导出

首先来推导伴随抛物化稳定性方程，考虑LPSE方程为：

其中：

为了推导出APSE，需要给出内积的定义：

这样，依据伴随算子的定义，可以利用分步积分方法导出线性微分算子L的 伴随形式L*：

其中，上标“*”表示伴随形式；上标“H”表示转置复共轭；坐标x1、x2、x3分别代表流动的流向、展向和法向；B.C部分是由于分步积分导致产生的，实际上是描述伴随模态和原模态在边界处的恒等关系。依照伴随算子的定义，不难有：

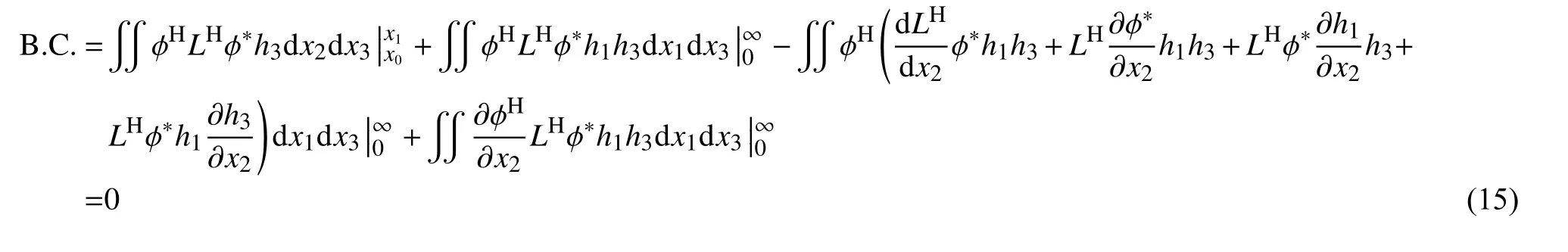
通过分步积分，也能推导出线性抛物化稳定性方程的伴随形式：

其中：

其系数矩阵元素的具体表达形式见Airiau等的文章[12]。根据伴随算子的性质，伴随算子特征值与原算子的特征值互为共轭。这就意味着，在其中一个问题的特征值已知的情况下，其伴随问题的特征值不需要再进行计算，只需要带入前面计算所求出的特征值即可。同时，对流项前面的符号决定了流向差分格式方向，因此LPSE问题利用后差从前向后推进求解，而APSE问题利用前差从后向前推进求解。除此之外，LPSE和APSE的离散格式相同。

这里需要指出的是，由于根据伴随算子的性质，实际上是基于APSE和LPSE给出的流向复波数α是相同的。但对于扰动演化过程来说，除了流向复波数α，扰动的形函数变化也是需要被考虑的。因此在使用APSE计算扰动的演化过程中，还需要在使用APSE计算得到α沿流向不同位置的分布之后，再使用一次LPSE计算形函数沿流向的变化。这样就可以给出扰动增长率的分布了。

2.2 APSE求解器的验证

依照上面的公式推导构造了APSE的求解器。为了验证该求解器的正确性，选取高超声速平板边界层中第二模态扰动的演化[13]作为对象。用LPSE给出的Mack模态演化过程即增长率的分布作为比较基准，将利用APSE求解器计算的所得到的扰动增长率与LPSE的结果进行对比，从而对APSE进行验证。其中基本流为二维平板边界层Blasius相似解，自由来流参数如表3所示，壁面边界条件为无滑移边界条件和等温条件。

表3 算例2的主要计算参数Table 3 Main calculation parameters of Case 2

在入口引入第二模态的增长扰动。分别使用LPSE和基于APSE计算扰动演化过程的方法计算其增长率分布。图4给出了用不同的方法计算得到的扰动增长率沿流向的变化。APSE给出的第二模态增长率变化与LPSE的预测结果基本一致。这表明用APSE的方法计算扰动的线性增长率是可靠的。

图4 Case 2中LPSE与APSE增长率对比Fig. 4 Comparison of the growth rates calculated by LPSE and APSE in Case 2

需要额外指出的是，从图4中可以看到增长率存在微小的差别。这种差别主要是由于在LPSE和APSE计算过程中，用于迭代求解复波数α的范数存在差异。虽然约定的范数保证了扰动形函数沿流向的慢变性。但是这种差异会造成抛物化方程在省略二阶小量项的过程中存在一些很小的差别，这种差别造成了即便使用同样的公式（10）计算增长率，也不是完全一样的。

2.3 中性曲线下支的求解过程

首先，在增长区选取一点x1，给定该位置处伴随O-S方程的解。接着，以该解为基础用伴随抛物化稳定性方程（APSE）从下游向上游推进求解，一直求解到中性曲线以外的区域（特征是伴随PSE给出的特征值虚部为负，这里可以设置为-0.005以下水平），然后，在伴随方程求解的终止点x0的位置处求解一次O-S方程（特征值初值为伴随方程在该处的特征值的共轭），求出O-S方程的特征函数。然后以O-S方程给出特征函数以及APSE确定的特征值的共轭为基本条件作为LPSE方程的入口计算LPSE，但在用LPSE进行计算时，不需要再计算特征值，而是直接利用伴随方程给出的特征值，求解出LPSE的形函数。最后通过对LPSE给出的扰动演化进行处理，得到增长率的分布，从而确定某一频率下扰动中性曲线的下支。

2.4 使用APSE在不同工况下确定中性曲线下支界

为了进一步检验以上求解中性曲线下支界的方法，选取了三种不同的情况进行应用。由于Mack模态的激发源于快模态和慢模态的同步作用，那么可以从LST对快、慢模态演化并同步的过程来刻画这种激发过程。这种激发过程多见于以下三种情况[14-15]：上游快模态增长或衰减较慢但下游慢模态与不稳定的Mack模态相连；上游慢模态增长或衰减较慢，并且在下游与不稳定的Mack模态相连；上游快模态增长或者衰减较慢，并且下游与不稳定的Mack模态相连。所选取的三种工况正是对应于以上提到的三种情况，其主要计算参数见表4。以下则分别针对不同工况讨论计算结果。

表4 不同工况的主要计算参数Table 4 Main calculation parameters of different flow conditions

2.4.1 Case 1

图1和图2已经分别给出了Case1条件下线性稳定性理论得到的快、慢模态的增长率和相速度的实部沿流向的变化。从图中可以看出，根据LST分析的结果，在中性曲线的上游，快模态和慢模态都是衰减的。相比而言快模态的衰减率小一点。在下游约x= 200位置处，快、慢模态的相速度接近，该处为同步点，同步点之后慢模态连接的是一个增长很快的第二模态，而快模态变为一个稳定的模态。显然，该算例对应于上游快模态增长或衰减较慢但下游慢模态与不稳定的Mack模态相连的情况。

为了给出更为准确的中性曲线，分别用线性抛物化稳定性方程（LPSE）以及伴随（APSE）的方法来计算。其中，选取上游某一位置的LST的解为初值，用LPSE的方法向下游进行演化计算的入口扰动参数如表2所示。

图5给出了用不同的方法计算所得到的预测结果。可以看到，LST给出的第二模态中性曲线下支约为x= 220。此时不管入口给快模态还是慢模态，扰动的增长率都有一个波动过程，即都对应于前面提到的“拍”结构。这主要是由于在流场的下游位置慢模态占主导地位，而在流场的上游位置是快模态占主导地位，因此在上游的位置，首先存在着一个慢模态到快模态的模态动态切换过程，但这个过程随着扰动逐渐向下游演化，下游流场又由慢模态所主导。相比入口给快模态，入口给慢模态时能量更容易得到积累，尤其是考虑流动的非平行性之后。

图5 Case1中不同方法给出的扰动波增长率沿流向分布的比较Fig. 5 Comparison of the growth rate distributions along the flow direction given by different methods in Case 1

从图中还可以观察到当在流向位置x= 160之后，慢模态的增长率就已经比快模态的增长率大了，此时慢模态在中性曲线的下支上游就已经开始逐渐占据了主导地位。因此在流场的更下游主要体现还是慢模态的扰动，此时LPSE给出的Mack模态中性曲线下支位置约为x= 210。同时还可以看到在上游某一位置分别选取慢模态和快模态的解为初值，向下游进行LPSE计算时，所得到的中性点的位置存在较大差异。本算例中，在上游离散模态扰动向下游演化的过程中，在流向位置x= 160之后的区域由于慢模态具有更大的增长率，快模态的幅值越来越小，慢模态的幅值越来越大，进而激发第二模态的不稳定波。

相比于LPSE的计算结果，当用APSE方法来计算小扰动的稳定性特征时，从下游增长的Mack模态开始跟踪扰动到上游的历史演化历程，利用APSE可以跟踪得到是上游的慢模态的演化从而主导了下游的不稳定波模态。此外，从图中也不难看到在x= 160以前的区域，APSE的预测结果也存在对应的“拍”结构，因此该方法也可以很好的描述离散模态之间的切换过程。经过比较，还可以发现，通过APSE的方法来计算所得到的增长率的结果与入口扰动选取慢模态的PSE计算的演化结果基本一，所确定得到的中性曲线下支非常接近于LPSE入口选取慢模态的所得到的结果。这说明该方法是合适的。

2.4.2 Case 3

图6和图7分别给出了Case 3状态下线性稳定性理论得到的快、慢模态的增长率和相速度沿流向的变化规律。从图中可以看出，在靠近前缘处，慢模态为增长的第一模态，快模态一直是衰减的。在向下游发展的过程中，慢模态的相速度增加，而快模态的相速度减小，在下游约x= 380位置处，快、慢模态的相速度的实部接近，这个位置被称为同步点，同步点之后慢模态连接的是一个增长很快的第二模态，而快模态变为一个很稳定的模态。显然，该算例对应于上游慢模态增长或衰减较慢并且在下游与不稳定的Mack模态相连的情况。

图6 Case 3由LST给出的快、慢模态增长率沿流向分布Fig. 6 Growth rate distribution along the flow direction given by LST for the fast and slow modes in Case 3

图7 Case 3由LST给出的快、慢模态相速度沿流向分布Fig. 7 Phase velocity distribution along the flow direction given by LST for the fast and slow modes in Case 3

下面分别用线性抛物化稳定性方程（LPSE）以及伴随抛物化稳定性方程（APSE）的方法来进行计算和比较。其中，选取上游某一位置LST的解为初值，用LPSE的方法向下游进行演化计算的入口扰动参数如表5所示。

表5 Case 3的入口扰动参数Table 5 Entrance disturbance parameters in Case 3

图8给出了用不同方法给出的扰动增长率的预测结果。LST给出的第二模态中性曲线下支约为x=380。当上游入口扰动给定为快模态进行LPSE计算时，此时增长率沿流向存在着一个分布，这是由于在散射作用下，快模态向慢模态投影，在两个模态的共同作用下，流场中的扰动表现为两模态叠加，从而形成的“拍”的效应。由于上游慢模态增长率较大而快模态增长率较小，因此存在着扰动由快模态向慢模态转换的过程，但即便如此LPSE给出的中性曲线下支位置约为x= 400；而当上游入口扰动为慢模态时，增长率沿流向分布较为光滑，这是由于此时慢模态在上游占主导地位，虽然也存在着慢模态向快模态由于散射效应的投影，但是流场主要体现还是慢模态的扰动，此时LPSE给出的Mack中性曲线事实上与第一模态中性曲线相接，没有真正的Mack模态中性曲线下支，而对应于该频率扰动增长率最小值的流向位置在x= 305左右。显然，在上游某一位置分别选取慢模态和快模态的解为初值，向下游进行LPSE计算时，所得到的中性点的位置存在较大差异。

图8 Case 3中不同方法给出的扰动波增长率沿流向分布的比较Fig. 8 Comparison of the growth rates along the flow direction given by different methods in Case 3

在本算例中，随着上游离散模态扰动向下游演化，由于慢模态具有更大的增长率，快模态的幅值越来越小，慢模态的幅值越来越大，即慢模态起主导作用，进而激发第二模态的不稳定波。相比之下，当采用APSE方法来计算小扰动的稳定性特征时，从下游增长的Mack模态开始跟踪扰动到上游的历史演化历程中可以看到，是上游的慢模态的演化从而主导了下游的不稳定波模态，并且此时通过APSE的方法来计算所得到的增长率的结果与入口扰动选取慢模态的LST解进行LPSE计算的演化结果基本一致，所确定得到的中性曲线下支非常接近于入口选取慢模态进行LPSE计算所得到的结果。这也就说明本文的方法是合理的。

2.4.3 Case 4

图9和图10分别给出了Case 4状态下用线性稳定性理论（LST）得到的快、慢模态的增长率和相速度沿流向的变化规律。从图中可以看出，在中性曲线的上游，快模态的衰减率相对更小，是主导流场的离散模态。同步点大概对应于x= 400的位置，同步点之后快模态连接的是第二模态，而慢模态变为一个很稳定的模态。显然，该算例对应于上游快模态增长或衰减较慢，并且在下游与不稳定的Mack模态相连的情况。

图9 Case 4由LST给出的快、慢模态增长率沿流向分布Fig. 9 Growth rate distribution along the flow direction given by LST for the fast and slow modes in Case 4

图10 Case 4由LST给出的快、慢模态相速度沿流向分布Fig. 10 Phase velocity distribution along the flow direction given by LST for the fast and slow modes in Case 4

与前面的算例类似，依然分别用线性抛物化稳定性方程（LPSE）以及伴随（APSE）的方法来进行计算。其中，选取上游某一位置的LST的解为初值，用LPSE的方法向下游进行演化计算的入口扰动参数如表6所示。

图11给出了用不同方法计算得到的扰动增长率的预测结果。LST给出的第二模态中性曲线下支约为x= 360。同时，由LPSE给出的结果表明，当入口扰动为快模态时，中性曲线下支对应于x= 350的位置；而当入口扰动为慢模态时，中性曲线下支对应的是x= 380。显然，在上游某一位置分别选取慢模态和快模态的解为初值，向下游进行LPSE计算时，所得到的中性点的位置存在较大差异。本算例中，随着上游离散模态扰动向下游演化，由于快模态具有更大的增长率，慢模态的幅值越来越小，快模态的幅值越来越大，即快模态起主导作用，进而激发第二模态的不稳定波。同样的，当给定上游非主导作用的慢模态时，LPSE给出的预测结果中依然可以观察到慢模态向快模态的切换过程所产生的“拍”结构。也正是因为存在着这样的切换过程，因此当入口给定慢模态时所给出的中性曲线下支位置更为靠后。

表6 Case 4的入口扰动参数Table 6 Entrance disturbance parameters in Case 4

图11 Case 4中不同方法给出的扰动波增长率沿流向分布的比较Fig. 11 Comparison of the growth rate distributions along the flow direction given by different methods in Case 4

相比而言，当采用APSE方法来计算小扰动的稳定性特征时，可以看到从下游增长的Mack模态开始跟踪扰动到上游的历史演化历程，利用APSE可以跟踪得到是上游的快模态的演化从而主导了下游的不稳定波模态，并且此时通过APSE的方法来计算所得到的增长率的结果与入口扰动选取快模态的LST解进行的PSE计算的演化结果基本一致，所确定得到的中性曲线下支非常接近于LPSE入口选取快模态的所得到的结果。这也就说明本文的方法可以客观的给出第二模态中性曲线下支点的位置。

2.5 对方法和结果的讨论

以上给出了三种基于APSE计算中性曲线下支的结果，并且与LPSE的分析进行了对比。从对比结果不难发现不管对于哪种情况，APSE都可以取得与LPSE一致的结果。这说明，本文这种方法是可以用来预测考虑感受性的中性曲线下支界的。相比LPSE方法而言，APSE只需要直接从Mack模态增长区开始向上游计算，在此过程中需要使用约定范数来使得伴随形函数保证沿流向缓变。在此基础之上，再利用LPSE计算时，只需要直接使用APSE给出的α即可，不再需要迭代过程。这样比起LPSE方法来看，效率更高，而且有效解决了LPSE解决该方法需要分别计算快、慢模态演化的问题。

观察以上三种情况的对比结果，我们不难发现，APSE给出的结果实际上始终对应于LPSE最终可以更易增长演化到的那一支。这是由于，不管是APSE还是LPSE方法，实际上给出的都是扰动的整体演化过程。在边界层非平行性的前提下，依靠散射效应，实际上流场中两种离散模态是共存的。而LPSE或者APSE则给出了这两种模态叠加之后的演化结果。在这样的前提下，其演化结果实际上反映了流场中整体的对各种扰动的促进或者抑制能力。因此，当使用APSE来从Mack第二模态开始从下游向上游推进计算时，它给出的结果实际上是捕捉了更容易激发或者演化到Mack模态的离散谱。这也就是为什么基于APSE的方法可以准确地描述出考虑感受性的中性曲线下支界。

3 结 论

高超声速边界层中性曲线下支的确定对于感受性分析以及eN转捩预测具有一定的意义和价值。本文首先用LPSE和LNS方法分别对边界层内快、慢模态激发第二模态不稳定波的过程进行了研究。从计算结果上来看，这两种方法给出的Mack第二模态中性曲线下支位置一致，但是使用LPSE计算的效率相对更高。除此以外，我们还发现在使用LPSE确定中性曲线下支时，存在着衰减区离散模态求解困难以及需要计算两个离散模态的演化过程才能给出中性曲线下支点的问题。

基于以上LPSE求解时存在的问题，本文提出了一种基于伴随抛物化稳定性方程（APSE）的方法来确定中性曲线下支。该方法可以考虑流场的非平行性的影响，同时由于伴随方程可以引入下游的不稳定的Mack模态扰动为入口来进行计算，因此可以有效的改善基于LPSE方法求解时的不足。由于Mack第二模态的激发实际上源于快模态和慢模态的同步作用，从LST对快、慢模态演化并同步的过程的刻画多见于以下三种情况：上游快模态增长或衰减较慢但下游慢模态与不稳定的Mack模态相连；上游慢模态增长或衰减较慢，并且在下游与不稳定的Mack模态相连；上游快模态增长或者衰减较慢，并且在下游与不稳定的Mack模态相连。因此本文选取了这三种典型的Mack第二模态生成的过程进行了中性曲线下支的计算。从计算结果上来看，该方法给出的中性曲线下支与正确选取上游离散模态时，LPSE方法给出的结果较为吻合。该方法可以进行有效的推广，与eN方法结合用于高超声速边界层的转捩预测问题和稳定性分析问题的研究。