二类不均衡数据分类问题常用策略研究

杨小军，刘 志，王力猛，刘 文

（国防大学 联合勤务学院，北京 100858）

0 引 言

分类是数据挖掘领域的一类重要问题，现有的分类方法都很成熟，如决策树、支持向量机、朴素贝叶斯方法等，并利用这些方法成功地解决了许多实际问题。但随着应用范围的扩大和研究的深入，分类方法在使用过程中遇到了数据样本分布不均衡问题。通常称数据分布不均衡的数据集为不均衡数据集，数据分布不均衡表现为两种形式：一是类间数据分布不均衡；二是在某一类样本的内部存在着类内不均衡。在不均衡数据集中，将样本数量少的类称为少数类或正类，样本数量多的类称为多数类或负类。

对不均衡数据进行正确分类，是数据分类的一个难题。问题来源于不均衡数据集的样本分布特点，以及传统分类算法固有的局限性。传统分类算法的重要前提是：数据集中各样本比例是均衡的；以总体最大精度为目标，很容易忽略少数类；所有的分类错误代价都相同。因此，如果用传统的分类器来直接处理不均衡数据集，会造成少数类样本的分类精度较差，尤其是数据不均衡严重时更是如此。鉴于目前研究不均衡分类问题都是基于不均衡的两类问题，则本文主要研究比较二类不均衡数据分类问题的常用策略。

1 不均衡数据分类策略

常用的不均衡数据分类策略主要有如下几类：在数据层面，通过重采样来解决数据分布不均衡状况；在算法层面，通过代价敏感算法或是集成算法提升不均衡数据分类时的性能；通过数据层面与算法层面相结合的策略进行改进。

1.1 数据层面的处理方法

由于不均衡数据集是数据样本之间比例不均衡，可通过对各类别数据的增删，重新实现不同类别数据样本之间的平衡。数据重采样是最具代表性的数据层面处理办法，可将其分为欠采样、过采样，以及二者结合的混合采样方法。最简单的重采样为随机过采样（ROS）方法和随机欠采样（RUS）方法。通过简单复制／删除部分样本的方式，达到平衡二类样本比例的目的。而随机方法的缺点是增加了过学习的概率。因此目前考虑更多的是启发式方法。

Chawla提出的SMOTE［1］方法，是一种经典的启发式过采样方法。SMOTE方法首先为每一个少数类样本随机地挑选出几个相邻的样本，然后在这个少数类样本和挑出的邻近样本的连接线上，以随机方式取点，生成没有重复的少数类样本。因此，在很大程度上解决了随机过采样方法产生的过拟合问题。此后，在SMOTE方法的基础上形成了大量的改进算法：如D-SMOTE过抽样算法，是采用求最近邻样本均值点的方法来生成少数类样本；N-SMOTE算法［2］，则采用了周围空间结构信息的邻居计算公式来生成少数类样本等等。

启发式欠采样方法为达到更好的分类效果，采用方法去除掉那些远离分类边界的、有数据重叠的、且对分类作用不大的多数类样本。典型的欠采样方法有Tomek links方法［3］和ENN方法等。Tomek links方法是先判断两个不同类样本之间是否构成了Tomek links，是则进行样本剪辑；ENN算法的基本思想是，删除离每个多数类样本最近的3个近邻样本中的2个。在实际应用中，为了达到最佳效果，一般将各种欠采样和过采样方法混合使用。在增加少数类数据样本同时，减少了多数类数据样本，最终达到两类数据样本平衡的目的。SMOTE+Tomek links、SMOTE+ENN［4］是典型的混合采样方法。

1.2 算法层面处理方法

在算法层面，不均衡数据学习常用的方法有：代价敏感算法、集成学习方法、单类学习方法和特征选择方法。

1.2.1 代价敏感算法

传统分类器以实现样本整体误差最小为最终目标。在训练过程中，由于数量偏少的缘故，少数类样本的预测准确率很低，甚至出现被忽略的情况。为了提升少数类的重要程度，代价敏感算法给少数类样本造成的误差施加更大的惩罚。算法的中心思想是：运用该方法训练分类器的目标是最小化样本的整体误分代价，不再追求实现样本整体误差最小化。代价敏感算法的核心是代价矩阵的设计，其设计是否合理，最终决定了分类模型的性能。在二分类问题中，代价矩阵见表1。

表1 二分类问题的代价矩阵Tab.1 The cost matrix of binary classification

其中，Cij表示第i类样本被误分成j类的代价，应赋大于0的值。左对角线上的元素Cii表示被正确分类的代价，其取值应为0。重要的类别应赋更大的代价，如Cij＞Cji表示第i类样本比第j类更重要。在类不均衡学习中，一般更为关心少数类样本。如癌症检测中的指标异常、机器故障检测中出现的异常等。因此可将少数类视为重要类，在代价敏感学习中赋予更大的错分代价［5］。但误分代价具体取值难以确定。

1.2.2 集成学习算法

集成算法是将多个弱分类器组合构造成一个强分类器。由于单个算法能力有限，找到的多数是局部最优解，而非全局最优解。集成学习算法对多个局部最优解进行综合，可以提升分类器的性能，已被证明是一种能有效解决不均衡问题的技术。典型的集成算法有装袋方法（Bagging）和提升方法（Boosting），其主要思想是先对训练集进行不同方式的训练，得到不同的基分类器；再对基分类器进行组合，最终达到提升集成分类器学习效果的目的。在Bagging算法中，为了提高集成分类器泛化能力，以有放回的方式从原始训练集中随机选取出若干样例形成训练集，多次选取不同训练集以增加基分类器差异度。AdaBoost算法是Boosting方法中的代表，通过在迭代中加大被错误分类样本的权重，减少被正确分类样本的权重，由有差异的训练样本集得到不同的基分类器，最终经过加权集成为最终的分类器。在迭代过程中，Bagging算法每个样本的权重都一样，而Boosting算法却能够根据样本的错误率不断调整样本的权重。因此，在处理不均衡分类问题时，基于Boosting的算法在一定程度上优于基于Bagging的算法［6］。

在实际处理不均衡数据分类时，通常将数据层面的方法与算法层面的方法相结合，解决不均衡分类问题。如，将采样技术和集成算法结合。其中最典型的是Nitesh V.Chawla提出的SMOTEBoost［7］方法。该方法通过结合SMOTE过采样技术和AdaBoost提升方法，来解决不均衡数据分类问题。SMOTEBoost算法在训练开始前，先使用SMOTE方法生成少数类样本，再使用Adaboost方法对样本分类，提升了少数类样本的分类准确率，避免了过拟合。此外，将采样和代价敏感算法相结合，也是不均衡数据学习的一类重要方法。

对常用的集成算法进一步集成就形成了混合集成算法。为防止采用降采样技术后，造成多数类样本信息丢失的情况，Liu等提出EasyEnsemble和BalanceCascade算法［3］。EasyEnsemble算法首先利用Bagging技术对多数类样本进行多次有放回随机采样，形成多个与少数类样本数量相同的多数类样本子集；接着将每个多数类样本子集与少数类样本组合，用AdaBoost方法训练分类器；最后将所有的多数类子集所形成的分类器再组合。BalanceCascade算法与EasyEnsemble算法的原理类似，区别之处在于每一次形成多数类样本子集时，已正确分类的多数类样本将被从多数类样本集中去掉。

此外，单类学习方法是在分类时，只识别样本中的少数类，主要应用于异常检测领域。特征选择从已知的特征集合中选择出代表性特征子集，从而保留原数据的主要信息，其目的是去除冗余特征。在不均衡数据集中选出关键的区分特征，将会增强少数类和多数类的区分度，提升分类器中少数类和整体的正确率。

2 不均衡数据分类器评估指标

评价分类器性能的指标有查准率、召回率（查全率）、F-meas ur e、A U C等。对于传统分类器来说，数据集中多数类和少数类的分布大致保持均衡，分类准确率是最常用的性能评价指标。对不均衡数据集，则不能用准确率去评价一个分类器的好坏了，而常用G-mean和F-measure、A U C作为分类器性能的评估指标。

表2表达的是二类分类结果的混淆矩阵。表中T P和T N分别表示被正确预测的正类、负类样本数，F P和F N则分别表示被错误预测为正类的负类样本数和被错误预测为负类的正类样本数。因TP+T N是分类器正确预测的样本数，F P+F N则是分类错误的样本数量，T P+T N+F P+F N是所有数据样本数量。则分类准确率Acc可以由式（1）得出：

表2 分类结果的混淆矩阵Tab.2 Confusion matrix of classification results

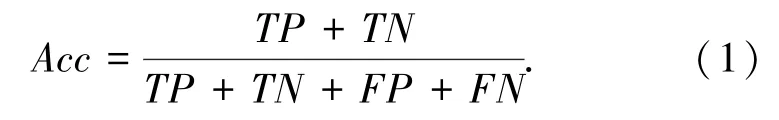
查准率P r eci s i on、召回率（查全率）R ecal l、真正率TP R、真负率T N R等指标，也可由这4个变量，通过以下各式得到：

其中，查准率和召回率是一对矛盾的度量指标，一个指标高时，另一指标往往偏低。为实现两者之间的平衡，将其合并为一个F-mea s u r e度量。只有当查准率和召回率都高时，F-mea s u r e的值才会大，其计算公式如下：

此外，采用G-mean来衡量真正率T P R和真负率T N R之间的关系。只有当正类和负类的准确率同时都高时，G-mea n值才会高，G-mean值可用来衡量不均衡分类器的整体准确率，其计算公式如下：

在不均衡数据学习中，还有一种常用的性能评价标准：受控者操纵特征曲线下面积（A U C）。受控者操纵特征曲线（R O C）显示了分类模型真正率和假正率之间的关系，是对各样本的决策输出值排序而形成的。R O C曲线下的面积就是AU C测度，A U C能很好地评价不均衡分类器的泛化性能。

F-measure、G-mean与A U C的取值范围均为［0，1］，分类器性能与其值成正比，即指标值越大，分类器性能越好。

3 各种策略分析实验

各种处理不均衡数据集的方法各有优劣。在不同的应用场景下，对各种不同的数据类型，需要采用不同的处理方法。下面对常用的3种类不均衡分类策略：重采样方法、代价敏感学习、集成学习及其组合方法进行实验分析比较。本文试验数据来自于KEEL数据集（http：／／www.keel.es／），本文从中选取了10个样本数据集，见表3。使用基于Java语言的开源软件KEEL实现了不均衡数据集的分类学习。KEEL软件有专门的不均衡数据学习模块，集成了大部分主流的不均衡数据处理方法。实验采用G-mean和A U C值作为评价不均衡分类学习能力的指标，用G-mean值衡量分类器的准确率，A U C值衡量分类器的泛化性能，取值越大，性能越优。实验采用5折交叉验证法。实验环境具体配置为：处理器为Intel i7-4720 2.60GHz；8G内存；64位windows操作系统。

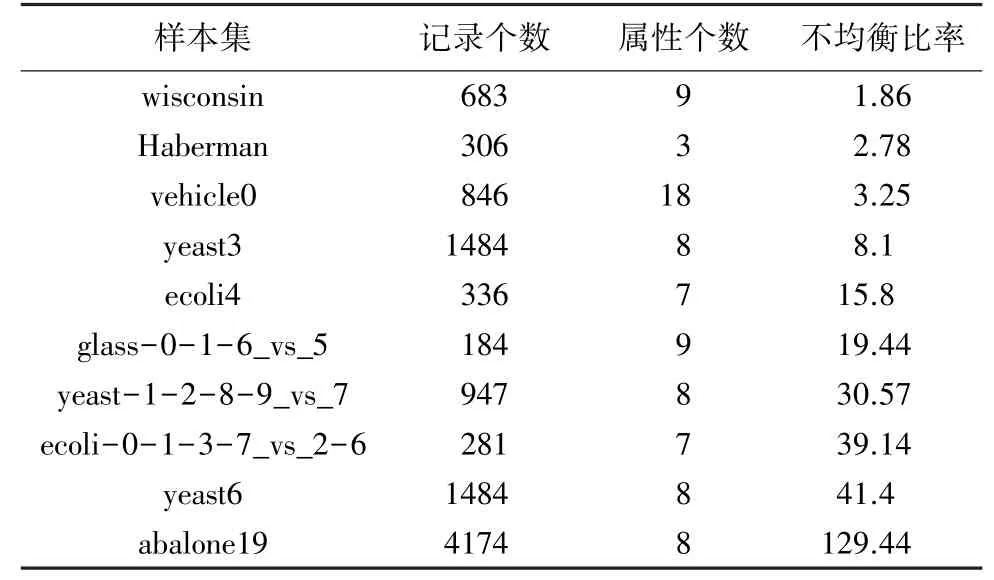
表3 不均衡数据集基本信息Tab.3 Basic information about imbalanced data sets

3.1 实验方法与结果

（1）重采样方法在不均衡数据集上的分类性能比较。实验选用了过采样方法SMOTE、欠采样方法Tomek links方法、混合采样方法SMOTE_Tomek links和SMOTE_ENN方法。通过重采样方法实现了数据集的再平衡之后，选用常用的决策树算法C4.5进行分类。各种重采样方法与C4.5算法的结合在不同数据集上的性能见表4。表中的TL表示Tomek links欠采样方法，SMOTE_TL表示SMOTE_Tomek links混合采样方法。

表4 重采样方法性能比较Tab.4 Performance comparison of resample method

（2）3种代价敏感算法在不同数据集上的性能比较。实验结果见表5。C4.5CS表示代价敏感决策树算法，SVMCS表示代价敏感支持向量机算法，NNCS表示代价敏感神经网络算法。

表5 代价敏感方法性能比较Tab.5 Performance comparison of cost-sensitive learning method

（3）重采样方法SMOTE和SMOTE_ENN方法性能比较。选用经典的重采样方法SMOTE和SMOTE_ENN方法，将其与代价敏感决策树算法C4.5CS进行组合，观察其是否比与普通决策树算法C4.5结合性能提升更大，结果见表6。

表6 重采样与代价敏感集成方法性能比较Tab.6 Performance comparison of ensemble learning method about resample and cost-sensitive learning

（4）经典集成方法性能比较。比较3种经典集成方法SMOTEBoost、EasyEnsemble、BalanceCascade在不同数据集上的性能，这3种集成方法均以C4.5决策树算法作为弱分类器，结果见表7。

表7 经典集成方法性能比较Tab.7 Performance comparison of classical ensemble learning method

3.2 实验结果分析

（1）重采样方法分析。根据表4的实验结果，过采样方法SMOTE在大部分数据集上的G-mean值和AUC值都高于欠采样方法Tomek links，只有在一个数据集“ecoli-0-1-3-7_vs_2-6”上出现例外，而且随着不平衡率的增加，二者之间的差值有逐渐增大的趋势，这说明SMOTE方法的性能全面优于Tomek links方法。混合采样方面，当不均衡率小于3时，SMOTE_TL采样方法的G-mean值和AUC值都高于SMOTE_ENN方法。不均衡率大于3后，SMOTE_ENN方法的G-mean值和AUC值普遍高于SMOTE_TL方法，说明SMOTE_ENN的准确率和泛化性能优于SMOTE_TL方法。比较SMOTE和SMOTE_ENN这两种相对更好的方法，当不平衡率在30以内时，SMOTE方法的G-mean值和AUC值高于SMOTE_ENN方法或是与其接近。当不平衡率超过30时，SMOTE_ENN方法的G-mean值和AUC值才会高于SMOTE方法。

（2）代价敏感学习方法分析。根据表5的实验结果，代价敏感支持向量机算法SVMCS的G-mean值和AUC值，大多数情况下都高于另外两种代价敏感算法。在不均衡比例较高时，代价敏感决策树方法C4.5CS的性能与代价敏感支持向量机算法SVMCS的性能相差不大，在两个数据集中C4.5CS的准确率与泛化性能甚至超过了SVMCS方法。当不均衡比例超过100时，如在“abalone19”数据集中，SVMCS的性能比另外两种代价敏感方法要高出很多。相比较而言，代价敏感神经网络算法的性能比另外两种算法差。

（3）重采样方法与代价敏感方法集成分析。根据表6的实验结果，当不平衡率小于10时，二种集成方法在不同数据集上所表现出的性能没有明显的规律可循。不平衡率在10～20时，SMOTE+C4.5CS集成方法的性能要强于SMOTE_ENN+C4.5CS集成方法。当不平衡率在20～100时则相反，SMOTE_ENN+C4.5CS方法的性能要强于SMOTE+C4.5CS方法。当数据分布严重不均衡时，SMOTE+C4.5CS方法的性能又超过了SMOTE_ENN+C4.5CS方法。总体而言，重采样方法与代价敏感方法的集成方法其性能表现出的规律性不强。

（4）C4.5为基分类器的3种经典集成方法比较分析。根据表7的实验结果，当不均衡率小于3时，EasyEnsemble方法的性能优于其它二种方法。不平衡率在8～30之间时，BalanceCascade的性能要强于SMOTEBoost方法和EasyEnsemble方法。当不均衡率超过40后，EasyEnsemble较另外两种集成方法重新取得了性能优势。当不均衡率超过100时，SMOTEBoost方法的G-mean值明显下降，AUC值也不如另外两种算法。

4 结束语

迄今为止，对于不均衡数据分类的理论成果非常少，本文所作的研究也只是在实验数据的基础上，总结出一些经验性的结果，迫切需要进行更深入的理论分析和研究。另外，目前研究不均衡分类问题都是基于不均衡的二分类问题，即使是不均衡的多类问题，也是通过将原问题分解成二类问题的方法去解决，并没有针对多类不均衡问题公认的评价指标。因此，需要进一步的深入研究，提出针对多类不均衡分类问题的评价指标和相应的学习算法。