基于优化灰色马尔科夫动态模型的上海港集装箱吞吐量预测

杜柏松　艾万政　胡林燕　刘然

摘要：

为更准确地预测港口集装箱吞吐量，以灰色马尔科夫模型为基础，建立一种优化的灰色马尔科夫动态模型。根据上海港集装箱吞吐量历史数据建立GM（1，1）预测模型。引入无偏灰色预测理论对GM（1，1）预测模型进行优化。构造等维信息模型，及时更新预测使用的数据以形成动态预测。利用马尔科夫理论对优化后的GM（1，1）预测残差值进行修正，得出上海港集装箱吞吐量的预测值。研究结果表明，与传统灰色马尔科夫模型相比，优化的灰色马尔科夫动态模型预测精度提高了37.03%，预测值拟合曲线更加贴近实际值曲线，预测结果有更高的可信度，为上海港集装箱吞吐量预测提供了一种新的方法。

关键词：

集装箱吞吐量; 灰色马尔科夫模型; 无偏灰色预测; 动态预测

中图分类号：  U691+.71

文献标志码：  A

收稿日期： 2020-06-03

修回日期： 2020-08-05

基金项目：

长江科学院开放研究基金（CKWV2019729/KY）;浙江海洋大学研究生教育質量系列工程项目（20190102）

作者简介：

杜柏松（1984—），男，山东菏泽人，船长，讲师，硕士，研究方向为航海安全保障、应用模型建模，（E-mail）dubaisong@zjou.edu.cn

艾万政（1971—），男，湖北浠水人，副教授，博士，研究方向为航海安全保障，（E-mail）aiwanzheng@126.com

Container throughput prediction of Shanghai Port based on

optimized grey Markov dynamic model

DU Baisong， AI Wanzheng， HU Linyan， LIU Ran

（School of Naval Architecture and Maritime， Zhejiang Ocean University， Zhoushan 316022， Zhejiang， China）

Abstract：

In order to predict the port container throughput more accurately， an optimized grey Markov dynamic model is established based on the grey Markov model. A GM（1，1） prediction model is established based on the historical data of Shanghai Port container throughput. The unbiased grey prediction theory is introduced to optimize the GM（1，1） prediction model. An equal dimension information model is constructed to update the data used for the prediction in time to form the dynamic prediction. Markov theoryis used to correct the predicted residual value of the optimized GM（1，1）， and the predicted value of Shanghai Port container throughput is obtained. The results show that， compared with the traditional grey Markov model， the prediction accuracy of the optimized grey Markov dynamic model is 37.03% higher， the predicted value fitting curve is closer to the actual value curve， and the predicted result is of higher reliability. It provides a new method for Shanghai Port container throughput prediction.

Key words：

container throughput; grey Markov model; unbiased grey prediction; dynamic prediction

0 引 言

港口集装箱吞吐量具有随机性、波动性、非线性等特点，科学地预测港口集装箱吞吐量对我国港口规划基础设施建设、研究港口营运管理策略、制定港口发展规划等都具有重要的意义。常见的港口集装箱吞吐量预测方法有很多：郭战坤等[1]考虑到时间序列中可能存在异常值，提出了基于局部异常因子的奇异谱分析与最小二乘支持向量机组合预测模型。冯宏祥等[2]分别应用经验模态分解（empirical mode decomposition，EMD）算法和季节自回归综合移动平均（seasonal auto regressive integrated moving average， SARIMA）算法，对各影响因素的分量分别进行预测，得出了间接型模型的预测精度高于直接型模型的预测精度的结论。丁文涛等[3]为消除集装箱吞吐量影响因素的多重共线性，利用偏最小二乘法原理建模，在港口集装箱吞吐量预测上取得了良好效果。郭睿[4]采用误差反向传播神经网络对港口吞吐量预测进行了深入研究。此外，还有指数平滑法、线性回归分析法等。上述方法的计算较为复杂、对历史数据要求较高。集装箱吞吐量体系是一个典型的灰色系统[5]， GM（1，1）预测模型具有需要历史数据少、预测精度较高、能反映系统长期发展趋势等优点，比较适合港口集装箱吞吐量预测。杨金花等[6]利用GM（1，1）预测了上海未来3年的集装箱吞吐量;陈昌源等[7]在GM（1，1）预测的基础上引入弱化算子理论对原始数据进行优化，在预测精度上相对于传统GM（1，1）预测模型有所提高;杜柏松等[8]将GM（1，1）与马尔科夫理论结合，构造了灰色马尔科夫模型，预测结果表明灰色马尔科夫模型预测效果更好，并能克服历史数据的波动性。近年来，国内外很多学者对GM（1，1）和灰色马尔科夫模型在实际问题中的应用进行了大量的研究[9-12]。然而GM（1，1）和灰色马尔科夫模型的计算过程有待简化，预测精度有待提高。

本研究对灰色马尔科夫模型进行优化，以简化计算过程、提高对港口集装箱吞吐量的预测精度。

1 港口集装箱吞吐量灰色预测模型

1.1 GM（1，1） 预测模型的建立

记第k年港口集装箱吞吐量为x（0）（k），以历年港口集装箱吞吐量为原始序列X（0）={x（0）（1），x（0）（2），…，x（0）（n）};称X（1）={x（1）（1），x（1）（2），…，x（1）（n）}为X（0）的一阶累加序列，

x（1）（k）=ki=1x（0）（i），k=1，2，…，n;称Z（1）={z（1）（2），z（1）（3），…，z（1）（n）}为X（1）的紧邻均值序列，z（1）（k）=12（x（1）（k）+x（1）（k-1）），k=2，3，…，n。

构造港口集装箱吞吐量一阶线性方程：

由式（1）和（3）即可求出港口集装箱吞吐量GM（1，1）预测模型的响应式：

对式（4）进行累减计算，即可得到港口集装箱吞吐量的GM（1，1）预测模型：

1.2 GM（1，1）的无偏优化

GM（1，1）是我国学者邓聚龙教授提出的，众多学者通过不断实践检验发现，该模型更适合于原始数据序列呈指数变化且变化速度不快的情景。吉培荣等[13]证明了GM（1，1）是具有偏差的模型，并提出了无偏GM（1，1）预测模型，这不仅使预测精度有了显著提高，而且简化了运算。因此，在构建港口集装箱吞吐量预测模型时，为消除GM（1，1） 的预测偏差，对GM（1，1）进行无偏优化。

首先根据GM（1，1）建模过程求得参数a和u，然后计算无偏GM（1，1）的参数：

最后，可得经过无偏优化的GM（1，1）：

优化后的GM（1，1）消除了GM（1，1）固有的预测偏差，预测精度得以提高，而且預测值可以直接根据式（7）求取，无须再进行累减，简化了计算过程。

1.3 无偏优化的GM（1，1）的动态优化

GM（1，1）预测的优点是需要的历史数据少（5个左右即可预测），能够充分利用有限的数据进行精度较高的预测，但仅适合于变化趋势明显且波动不大的数据序列，对于波动大的数据序列预测精度明显降低。在用GM（1，1）进行预测时，引入动态建模的思想，采用新陈代谢的方法，在预测过程中不断更新数据，舍弃旧的数据。即用数据

序列X（0）=（x（0）（1），x（0）（2），…，x（0）（k））获得k+1时刻的预测值后，对该数据序列进行更新：去掉x（0）（1），加入预测值0k+1，构成新数列X′（0），用来获得k+2时刻的预测值。

按照此方法在保持预测数据序列等维的同时，不断动态更新预测使用的数据，称作无偏优化的GM（1，1）动态预测模型。该模型不仅保留了GM（1，1）短期预测精度高的优点，还能充分利用已知数据提高预测精度。

2 优化的灰色马尔科夫动态模型

港口集装箱吞吐量实际值与GM（1，1）预测值之间的差值称为残差，可以把残差分布情况看作马尔科夫链状态[14]。马尔科夫预测最显著的特点是无后效性，即所预测的将来状态只与当前状态有关，与过去状态无关，这一特点刚好可以弥补灰色预测对波动性大的数据预测精度不高的缺点。传统灰色马尔科夫模型的建模原理为，将GM（1，1）预测与马尔科夫预测结合起来，利用马尔科夫预测修正GM（1，1）的预测值。具体建模过程如下：

首先，根据GM（1，1）的预测值计算出残差和相对误差：

其次，根

据残差序列值的相对误差分布情况，均等设置i个马尔科夫状态区间：

再次，计算状态转移概率矩阵，利用频率等于概率的原理，即pij=nij/ni（ni为状态Ei出现的总次数，nij为由状态Ei转移到Ej的数据个数），得到一步状态转移概率矩阵

假设残差系统的初始状态为

[WTHX]S[WTBX]0，经过n步发展变化后，状态变为

最后，通过比较各状态概率的大小，确定概率最大的状态为预测状态Ei=[Li，Ui]，从而可得灰色马尔科夫模型的预测公式：

式中：“±”在预测状态为“高估”时取“+”，在预测状态为“低估”时取“-”。

优化的灰色马尔科夫动态模型与灰色马尔科夫模型的计算原理和步骤是一样的，利用马尔科夫理论对优化后的GM（1，1）预测残差值进行修正。

3 模型精度检验

对GM（1，1）的检验一般采取均方差比值（C）检验和小概率误差（Δ）检验2种方式，用以判定所建模型的优劣。通过优化的灰色马尔科夫动态模型和传统灰色马尔科夫模型的建立过程可以看出，这两种模型均是采用相关数学方法对GM（1，1）进行优化，其实质还是GM（1，1）预测。因此，采用GM（1，1）的检验方式对优化的灰色马尔科夫动态模型和传统灰色马尔科夫模型进行检验，检验标准见表1。

4 上海港集装箱吞吐量预测

为实现对上海港集装箱吞吐量的预测，以表2中第2列数据（2006—2019年上海港集装箱吞吐量数据，来源于《上海市统计年鉴》）为原始序列，采用优化的灰色马尔科夫动态模型进行预测。同时，计算GM（1，1）和传统灰色马尔科夫模型的预测值，用以比较各模型的预测精度。

4.1 上海港集装箱吞吐量的GM（1，1）预测

2006—2019年上海港集装箱吞吐量呈现稳步上升趋势，但是该上升趋势线并非直线，而是有波动的，尤其是2007—2009年集装箱吞吐量受全球金融危机影响变化幅度很大，2010年以后重回升势，2010—2019年集装箱吞吐量的上升趋势有所放缓，但仍然有小幅波动。

根据上述优化的灰色马尔科夫动态模型的建立过程，首先对上海港集装箱吞吐量进行灰色预测。建立原始序列：

然后根据式（1）～（5）可得上海港集装箱吞吐量预测模型：

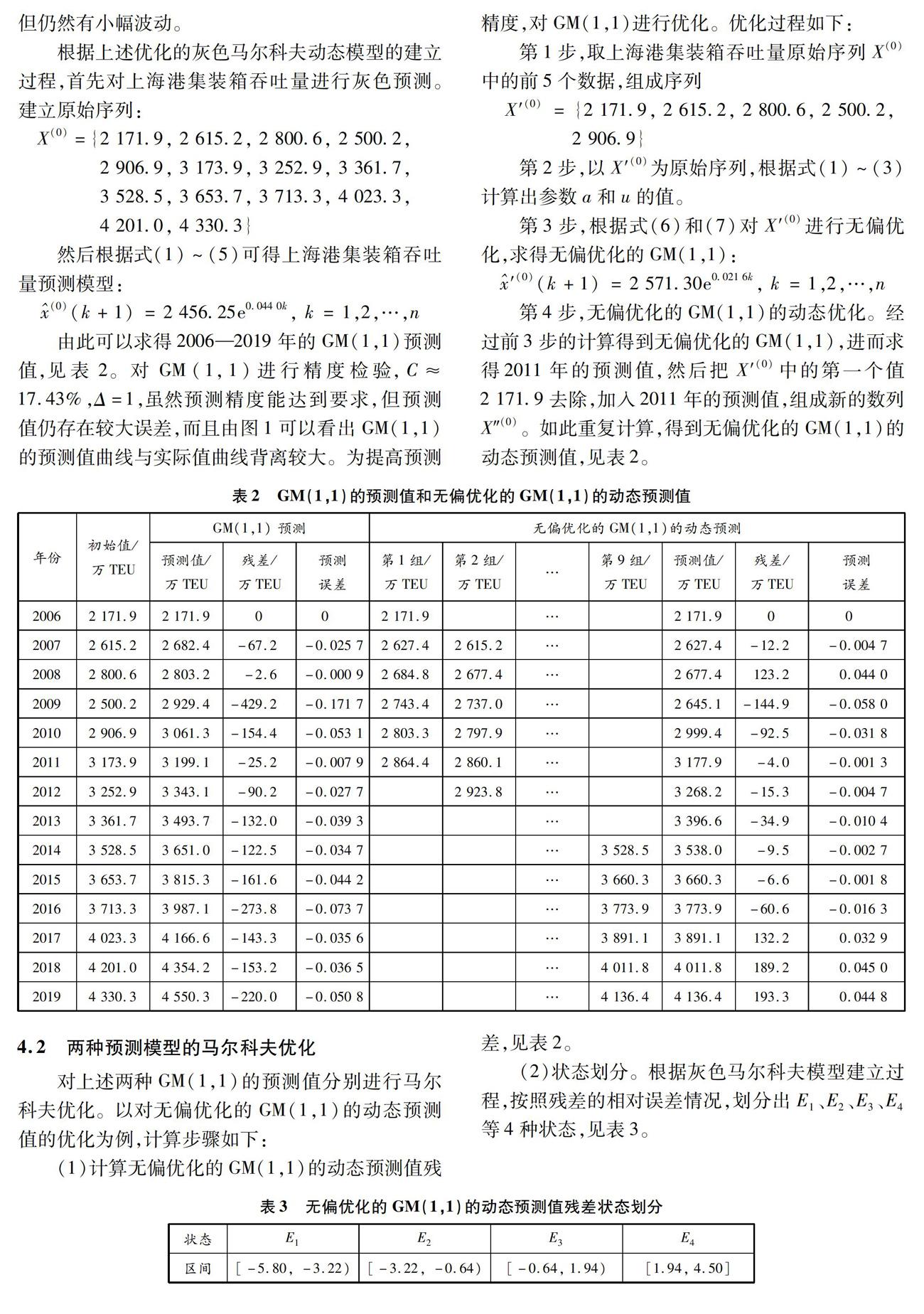
由此可以求得2006—2019年的GM（1，1）预测值，见表2。对GM（1，1）进行精度检验，C≈17.43%，Δ=1，虽然预测精度能达到要求，但预测值仍存在较大误差，而且由图1可以看出GM（1，1）的预测值曲线与实际值曲线背离较大。为提高预测精度，对GM（1，1）进行优化。优化过程如下：

第1步，取上海港集装箱吞吐量原始序列X（0）中的前5个数据，组成序列

第2步，以X′（0）为原始序列，根据式（1）～（3）计算出参数a和u的值。

第3步，根据式（6）和（7）对X′（0）进行无偏优化，求得无偏优化的GM（1，1）：

′（0）（k+1）=2 571.30e0.021 6k， k=1，2，…，n

第4步，无偏优化的GM（1，1）的动态优化。经过前3步的计算得到无偏优化的GM（1，1），进而求得2011年的预测值，然后把X′（0）中的第一个值2 171.9去除，加入2011年的预测值，组成新的数列X″（0）。如此重复计算，得到无偏优化的GM（1，1）的动态预测值，见表2。

4.2 两种预测模型的马尔科夫优化

对上述两种GM（1，1）的预测值分别进行马尔科夫优化。以对无偏优化的GM（1，1）的动态预测值的优化为例，计算步骤如下：

（1）计算无偏优化的GM（1，1）的动态预测值残差，见表2。

（2）状态划分。根据灰色马尔科夫模型建立过程，按照残差的相对误差情况，划分出E1、E2、E3、E4等4种状态，见表3。

（3）建立状态转移概率矩阵。根据表3，可得一步状态转移概率矩陣

进而得到多步状态转移概率矩阵

[WTHX]P[WTBX]n。

（4）计算无偏优化的GM（1，1）的动态预测值的修正值，即优化的灰色马尔科夫动态模型预测值。

2019年以前的预测值可以直接利用式（14）计算;对于2020年及以后年份的预测值，首先求出相应年份的无偏优化的GM（1，1）的动态预测值，然后以2016—2019年作为预测的基础年份，通过计算状态转移概率矩阵确定相应预测年份的状态，取其大者为预测状态，最后利用式（14）计算。

GM（1，1）预测值的优化方式同上。两种灰色马尔科夫模型的预测值见表4。

4.3 预测模型的误差分析

对上海港集装箱吞吐量预测模型进行误差检验：传统灰色马尔科夫模型的C≈7.29%，Δ=1;优化的灰色马尔科夫动态模型的C≈4.06%，Δ=1。根据检验标准（表1），两种模型的预测等级均为优，说明这两种模型均非常适合解决上海集装箱吞吐量预测问题。优化的灰色马尔科夫动态模型的C值更小，而且其平均误差比传统灰色马尔科夫模型的平均误差降低了37.03%，见表4。为直观比较GM（1，1）和两种灰色马尔科夫预测模型的预测精度，对预测值进行拟合，见图1。通过比较拟合曲线走势可知，优化的灰色马尔科夫动态模型预测值曲线的走势更接近原始值曲线。

4.4 上海港集装箱吞吐量预测

2020年初爆发的新冠肺炎疫情给集装箱的海运需求带来巨大影响，一方面各班轮公司为稳定市场运价大幅度削减运力，另一方面国际贸易量减少使集装箱运输需求降低。为体现疫情对上海港集装箱吞吐量的影响和提高预测精度，在使用马尔科夫理论修正无偏优化的GM（1，1）的动态预测值时，采用残差状态的“极端状态”。取2020—2022年这3年的状态为“E1=极度高估”，计算出优化的灰色马尔科夫动态预测值，见表5。

疫情发生以来上海港采取了“硬件提升”“软件升级”“抱团取暖”“加速推进和落实国家优惠政策”等一系列措施，尽最大努力克服疫情影响，使上海港集装箱业务逐步得以恢复[15]。由表5可以看出，2020年上海港集装箱吞吐量预测数据较2019年（4 330.3万TEU）有一定幅度下滑，2021年以后随着疫情稳定及世界经济的逐步恢复，集装箱吞吐量将再次出现增长，这基本符合上海港集装箱吞吐量的发展趋势，预测数据有较高的可信度。

5 结 论

（1）GM（1，1）能很好地解决上海港吞吐量发展趋势的预测问题，但却不能反映吞吐量数据波动的真实情况，结合马尔科夫预测的优点构建灰色马尔科夫模型，预测精度有了提高。通过对灰色马尔科夫模型进行无偏优化和等维信息理论动态优化后，预测精度有了大幅度提高，计算过程也得以简化。

（2）2020—2022年预测数据显示， 2020年上海港集装箱吞吐量受疫情影响有一定程度下滑，2021年开始再次恢复增长，该预测数据能基本反映上海港集装箱吞吐量实际情况，为上海市相关部门进行港口建设与开发等提供参考。

（3）在对优化的灰色马尔科夫动态模型的预测精度进行分析时发现，该模型预测结果的拟合曲线在2017年以后与实际值曲线有一定程度的背离，这是因为在利用马尔科夫模型对预测值进行修正时，取各状态的中间值进行修正，忽略了实际误差偏离中间值的程度。考虑采用相关算法对残差进行优化，期望进一步提高集装箱吞吐量的预测精度，这将是下一步的研究方向。

参考文献：

[1]郭战坤， 金永威， 梁小珍， 等. 基于异常值检测的港口集装箱吞吐量预测模型[J]. 数学的实践与认识， 2019， 49（17）： 26-34.

[2]冯宏祥， GRIFOLL M， AGUSTI M， 等. 基于数据分解的上海港集装箱吞吐量预测模型[J]. 中国航海， 2019， 42（2）： 132-138.

[3]丁文涛， 刘孟琦， 齐越， 等. 基于偏最小二乘法的集装箱吞吐量预测模型研究[J]. 港工技术， 2019， 56（6）： 28-32. DOI： 10.16403/j.cnki.ggjs20190606.

[4]郭睿. 基于BP神经网络的天津港吞吐量预测研究[D]. 天津： 天津大学， 2011.

[5]翟希东. 港口集装箱吞吐量预测模型研究[D]. 大连： 大连理工大学， 2006.

[6]杨金花， 杨艺. 基于灰色模型的上海港集装箱吞吐量预测[J]. 上海海事大学学报， 2014， 35（2）： 28-32. DOI： 10.13340/j.jsmu.2014.02.006.

[7]陈昌源， 戴冉， 杨婷婷， 等. 基于改进GM（1，1）模型的上海港集装箱吞吐量预测[J]. 船海工程， 2016， 45（4）： 153-156， 161. DOI： 10.3963/j.issn.1671-7953.2016.04.036.

[8]杜柏松， 朱鹏飞， 梁民仓， 等. 基于灰色马尔科夫模型的深圳港集装箱吞吐量预测[J]. 浙江海洋大学学报（自然科学版）， 2019， 38（2）： 180-186.

[9]HU Y C，JIANG P， LEE P C. Forecasting tourism demand by incorporating neural networks into grey-Markov models[J]. Taylor & Francis， 2019， 70（1）. DOI： 10.1080/01605682.2017.1418150.

[10]YAO Tianxiang，FORREST J Y， GONG Zaiwu. Generalized discrete GM（1，1） model[C]//Proceedings of 2011 IEEE International Conference on Grey Systems and Intelligent Services. IEEE， 2011： 4-12. DOI： 10.1109/GSIS.2011.6044149.

[11]高玲. 基于灰色马尔科夫组合模型的福州港吞吐量预测[J]. 太原理工大学学报（社会科学版）， 2012， 30（6）： 9-12， 59.

[12]汤天辰， 李林. 基于灰色马尔科夫模型的上海港集装箱吞吐量预测[J]. 物流科技， 2020， 43（3）： 105-108， 114.

[13]吉培荣， 黄巍松， 胡翔勇. 无偏灰色预测模型[J]. 系统工程与电子技术， 2000， 22（6）： 6-7， 80.

[14]时合生， 樊爱宛， 王巍. 用马尔科夫残差修正灰色理论的煤炭需求预测[J]. 计算机仿真， 2011， 28（10）： 187-190.

[15]王力. 上海港逐渐恢复繁忙. 陆路进港的出口集装箱数量达到正常水平[EB/OL]. （2020-03-16）[2020-06-03]. http：//shzw.eastday.com/eastday/shzw/g/20200316/u1ai20418079_k27223.html.

（編辑 赵勉）