基于改进PSO-ARIMA模型的船舶纵摇角度预测

王培良　张婷　肖英杰

摘要：

针对自回归移动平均（auto regressive moving average， ARMA）模型在船舶纵摇角度预测时不具有普遍适用性问题，提出使用自回归综合移动平均（auto regressive integrated moving average， ARIMA）模型进行纵摇角度预测，并采用改进粒子群优化（particle swarm optimization， PSO）算法对模型定阶。对纵摇角度值序列数据进行平稳性检验和差分运算，确定ARIMA模型的适用性;采用具有针对性适应度评价函数的PSO算法进行模型定阶，并优化PSO算法的权重计算方法。通过仿真对比验证本文所提方法的科学性和有效性。仿真结果表明：采用改进PSO算法进行模型定阶的方法能够有效提升模型的预测精度，具有更好的预测效果。

关键词：

自回归综合移动平均（ARIMA）模型; 粒子群优化（PSO）算法; 船舶纵摇; 纵摇预测

中图分类号：  U661.32+1

文獻标志码：  A

收稿日期： 2020-07-15

修回日期： 2020-09-22

基金项目： 国家自然科学基金（51909155）;潍坊市科学技术发展计划（2019GX075）

作者简介：

王培良（1987—），男，山东潍坊人，博士研究生，研究方向为载运工具运用工程，（E-mail）gfy5216@126.com;

张婷（1987—），女，山东聊城人，讲师，硕士，研究方向为航海技术，（E-mail）titi-507@163.com;

肖英杰（1959—），男，广东潮阳人，教授，博导，船长，研究方向为航海技术，（E-mail）xiaoyj@shmtu.edu.cn

Prediction of ship pitch angle based on improved PSO-ARIMA model

WANG Peiliang1，2a，2b， ZHANG Ting3， XIAO Yingjie2a，2b

（1.School of Intelligent Manufacturing， Weifang University of Science and Technology， Weifang 262700， Shandong， China;

2.a.Merchant Marine College; b.Engineering Research Center of Shipping Simulation，

Ministry of Education， Shanghai Maritime University， Shanghai 201306， China;

3.Navigation College， Shandong Transport Vocational College， Weifang 261206， Shandong， China）

Abstract：

In view of the fact that the auto regressive moving average （ARMA） model is not of the universal applicability when predicting the ship pitch angle， an auto regressive integrated moving average （ARIMA） model is proposed for predicting the ship pitch angle， and an improved particle swarm optimization （PSO） algorithm is adopted to determine the model order. For the pitch angle value series， the stationarity test and difference operation of the data are performed to determine the applicability of the ARIMA model. The PSO algorithm with a targeted fitness evaluation function is used to determine the model order， and the weight calculation method of the PSO algorithm is optimized. The scientificity and effectiveness  of the method proposed in this paper is verified through the simulation. The simulation results show that the method using the improved PSO algorithm determining the model order can effectively improve the prediction accuracy of the model and makes the model have better prediction effect.

Key words：

auto regressive integrated moving average （ARIMA） model;particle swarm optimization（PSO） algorithm; ship pitch; pitch prediction

0 引 言

船舶航行时受到外界环境（如风、浪、流等相互作用）的影响，产生六自由度的摇摆运动，严重威胁船舶的航行安全，因此，针对船舶摇摆随时间变化规律的预测研究是航运界的研究难点和热点[1]。

时间序列分析法是将预测对象的相关属性值按照时间顺序排列，然后结合数学模型研究其属性变化规律，从而对属性值进行预测[2-3]。文献[4]通过在护卫船上安装传感器采集数据，采用自回归移动平均（auto regressive moving average， ARMA）模型进行了船舶横摇姿态预报;文献[5]采用自回归（auto regressive， AR）模型，对船舶纵摇运动进行了自适应预报研究;文献[6]以艏前波法为基础，采用ARMA模型对船舶运动姿态进行了短时间高精度预报研究;文献[7]以船模水池实验为研究背景，使用线性AR模型进行船舶运动预报研究;文献[8]在AR模型的基础上，使用卡尔曼滤波算法对模型参数进行估计，对船舶运动进行实时估计，提高了模型预报的速度和精度;文献[9]使用AR模型对船舶运动进行预测，并使用格型递归最小二乘法对模型参数进行估计，提高了预报速度。

综上，在基于相关属性时间序列对船舶运动进行研究时[10]，AR模型[11]、ARMA模型等均能够进行有效预测，优化模型参数也对预测结果具有明显影响。然而，航行环境的随机性和波动性使得船舶纵摇角度值时间序列为方差、均值均存在变化的非平稳序列，因此，本文使用自回归综合移动平均（auto regressive integrated moving average， ARIMA）模型对船舶的纵摇角度进行预测，并且使用粒子群优化（particle swarm optimization， PSO）算法

进行模型定阶[12]，确定最优的ARIMA[13-14]模型并进行相应的纵摇角度预测。

1 理论与方法

1.1 ARIMA模型

ARIMA模型于20世纪70年代由BOX-JENKINS提出，其本质是将每个预测对象与相应的时间连接构建时间序列，用准确的数学模型描述该时间序列，并根据时间序列的性质预测未来值。记一个按时间顺序排列的随机事件序列为{xt}，则ARIMA（p，d，q）模型的表达式为

xt=1xt-1+2xt-2+…+pxt-p+

δ+εt+θ1εt-1+θ2εt-2+…+θqεt-q（1）

式中：p为AR模型的自回归项数;d为差分阶数;q为移动平均（moving average， MA）模型的移动平均项数;δ为常数项（表示序列数据没有零均值变化）;

{εt}为白噪声序列，其均值和方差分别为E（εt）=0

和D（εt）=σ2;i和θj（i=1，…，p;j=1，2，…，q）分别是xt和εt的参数，可用最大似然法等进行估计。

1.2 PSO算法

20世纪90年代初，Kenndy和Eberhart提出了PSO算法。该算法源于对鸟类捕食行为的研究：当鸟类捕食时，对每只鸟而言寻找食物最简单有效的方法就是搜索当前离食物最近的鸟所在的区域及周围区域。在PSO算法中，每个粒子代表一只鸟，同时代表所求问题的一个潜在解，每个粒子都有一个由适应度函数评价出的适应度值，用来表示当前解的优劣;同时粒子本身具有速度，其决定了粒子移动的方向和距离，速度根据自身及周围粒子的移动状态进行更新调整，从而实现全局寻优。算法在D维空间进行搜索，d=1，2，…，D。在每次迭代过程中，粒子i的速度和位置更新公式[15]如下：

式中：

k为当前迭代次数;

Pid，k为个体极值;Pgd，k为全局极值;vid，k为当前时刻粒子i的速度分量;

xid，k为当前时刻粒子i的位置分量;ω为惯性权重;加速度因子c1和c2为非负常数;

r1和r2为[0，1]内的随机数。

惯性权重ω的大小对算法的搜索能力具有显著影响：其值较大时，有利于全局搜索;其值较小时，有利于局部搜索。因此，为有效平衡全局搜索与局部搜索能力，使用线性递减权重：

ωk=ωk-（ωs-ωe）k/Tmax（3）

式中：ωs为惯性权重初始值;ωe为最大迭代次数时的惯性权重值;Tmax为最大迭代次数。

因此，迭代初期的较大权重值使算法保持较强的全局搜索能力;随着迭代的不断进行，惯性权重值逐渐减小，有利于算法进行准确的局部搜索。

1.3 ARIMA模型定阶

采用似然函數进行参数估计时，若数据样本量大，则能够不断提高模型的精度，但模型的复杂度也随之提升，同时带来参数估计中常见的过拟合现象。因此，需要对模型进行定阶。模型定阶也被称为模型识别，指确定ARIMA模型（式（1））中的p、q值。一般模型定阶采用AIC或者BIC准则，但有时其最终结果并非全局最优，因此，本文将这2个参数作为PSO算法的粒子位置信息进行优化求解，获得参数最优值及最优组合。

在使用PSO算法进行参数优化时，用适应度函数作为评价粒子性能优劣的主要指标，适应度值越大，参数值越符合模型。常采用均方误差或均方根误差评价ARIMA模型预测效果，因此，本文根据其思想设定适应度函数为

f（x）=1ni=1（yi-y^i）2（4）

式中：n为粒子数目;yi和y^i分别为研究对象的实际值和预测值。

由式（4）可知，预测值与实际值之间的差值越小，则适应度值越大，这说明粒子越合适，模型越理想，预测效果越好。

1.4 ARIMA模型构建流程

在使用ARIMA模型对船舶纵摇角度进行预测时，需要对纵摇角度值时间序列分别进行平稳性、白噪声等检验，确保研究对象的严谨，其具体步骤为：

①获得船舶纵摇角度值原始时间序列，并检查其平稳性;②若原始序列为非平稳序列，则对其进行差分运算，然后进行平稳性和白噪声检验;

③根据差分之后的平稳、非白噪声序列进行ARIMA模型拟合，使用PSO算法进行参数优化;④使用拟合获得的ARIMA模型进行研究对象的预测。

ARIMA模型构建流程见图1。

2 实验结果及分析

2.1 平稳性检验

为验证本文所提方法的科学性和有效性，以某船船首处的纵摇角度值为研究对象。该船为低速单机柴油机驱动、单桨、单舵船，属尾机型、方尾船型，其基本参数见表1。

在船舶航行过程中采集数据47次，每次采集100个样本值，以最后5次均值数据为检验序列，前42次均值数据为原始值序列，见图2。

分析图2可知，船首处的纵摇角度值序列存在非平稳性;通过计算得出序列的单位根检验统计量对应的P值为0.643 1，显著大于0.05。因此，原纵摇角度值序列为非平稳序列，需要对其进行差分，从而确定ARIMA模型参数d。

2.2 差分运算及白噪声检验

差分后的纵摇角度值序列见图3a。分析图3可知：差分后的纵摇角度值序列趋于平稳，其单位根检验统计量对应的P值为0.001，显著小于0.05，且自相关图也显示出短期相关性，因此可将差分后的纵摇角度值序列看作平稳序列。同时，基于残差的白噪声检验统计量为0.012 2，未明显大于显著水平，因此，可以认为差分后的纵摇角度值是平稳、非噪声序列。

2.3 模型定阶及预测分析

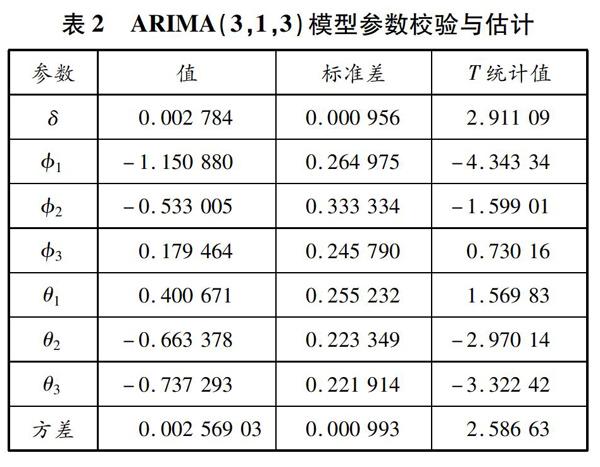
基于式（4）使用PSO算法进行计算，最终获得模型参数值分别为p=3、d=1、q=3，从而确定预测模型为ARIMA（3，1，3）。ARIMA（3，1，3）模型参数校验与估计见表2。

用ARIMA（3，1，3）模型进行预测，其结果见图4。由图4可知，ARIMA模型能够实现船首处纵摇角度值的预测，且实际值与预测值总体相差较小，表明预测模型较为准确，模型参数设置较为合理。

为验证利用PSO算法定阶的优势，采用传统BIC准则给ARIMA模型定阶，得到ARIMA（4，1，3）模型。将基于PSO算法定阶的ARIMA（3，1，3）模型与ARIMA（4，1，3）模型的预测结果进行对比，见图5。由图5可知：ARIMA（4，1，3）模型也能对船舶纵摇角度进行预

测，但其预测效果比ARIMA（3，1，3）模型的差;

两者在时间点3处的预测值均出现振荡。为进一步显示本文所提方法的优势，使用均方根误差（root mean squared error， RMSE）反映预测精度：ARIMA（3，1，3）模型预测结果的RMSE为0.037 94，小于ARIMA（4，1，3）模型预测结果的RMSE（0.057 24），这说明本文所述方法能够有效提升ARIMA模型的预测精度。

3 结 论

针对船舶纵摇角度值时间序列的非平稳性，采用自回归综合移动平均（ARIMA）模型进行纵摇角度预测，并使用对惯性权重进行改进的粒子群优化（PSO）算法进行模型定阶，设计适应度评价函数。通过仿真实验对比采用PSO算法定阶得到的ARIMA模型与采用传统BIC准则定阶得到的ARIMA模型的预测精度，结果表明：改进的PSO算法通过针对性的适应度评价函数能够提高ARIMA模型的预测精度，验证了本文所提方法的科学性和有效性。

参考文献：

[1]王培良， 吴晓芳， 张婷. 在航集装箱船摇摆姿态的概率模型[J]. 上海海事大学学报， 2017， 38（4）： 21-25. DOI： 10.13340/j.jsmu.2017.04.005.

[2]张腾， 任俊生， 范小晴， 等. 基于多系数保角变换法的船舶垂荡纵摇运动仿真[J]. 上海海事大学学报， 2019， 40（3）： 51-56. DOI： 10.13340/j.jsmu.2019.03.009.

[3]马建文， 涂兴华， 吴小峰， 等. 多自由度本船操纵运动仿真[J]. 上海海事大学学报， 2016， 37（4）： 32-35. DOI： 10.13340/j.jsmu.2016.04.006.

[4]BROOME D R， HALL M S. Application of ship motion prediction[J]. International Maritime Technology， 1998， 10（1）： 77-93.

[5]翁震平， 顧民， 刘长德. 基于二阶自适应Volterra级数的船舶运动极短期预报研究[J]. 船舶力学， 2010， 14（7）： 732-740.

[6]程超， 穆荣军， 蔡玲， 等. 基于遭遇波的艏前波法的航母姿态预报[J]. 中国惯性技术学报， 2015， 23（3）： 409-414. DOI： 10.13695/j.cnki.12-1222/o3.2015.03.024.

[7]马洁， 韩蕴韬， 李国斌. 基于自回归模型的船舶姿态运动预报[J]. 舰船科学技术， 2006， 28（3）： 28-30.

[8]彭秀艳， 王茂， 刘长德. AR模型参数自适应估计方法研究及应用[J]. 哈尔滨工业大学学报， 2009， 41（9）： 12-16.

[9]彭秀艳， 刘长德. 基于格型递归最小二乘算法的船舶运动极短期预报[J]. 船舶力学， 2012， 16（1/2）： 44-51.

[10]张泽国， 尹建川， 胡江强， 等. 基于减聚类ANFIS模型的船舶横摇运动实时预测[J]. 上海海事大学学报， 2017， 38（1）： 7-11， 67. DOI： 10.13340/j.jsmu.2017.01.002.

[11]BIANDejun， QIN Shiqiao， WU Wei，et al. A hybrid AR-DWT-EMD model for the short-term prediction of nonlinear and non-stationary ship motion[C]//2016 Chinese Control and Decision Conference. IEEE， 2016： 4042-4047. DOI： 10.1109/CCDC.2016.7531691.

[12]王培良， 张婷， 肖英杰. 蚁群元胞优化算法在人群疏散路径规划中的应用[J]. 物理学报， 2020， 69（8）： 240-248.

[13]SUHERMIN， SUHARTONO， PRASTYO D D，et al. Roll motion prediction using a hybrid deep learning and ARIMA model[J]. Procedia Computer Science， 2018： 251-258. DOI： 10.1016/j.procs.2018.10.526.

[14]TOUAMAH Y. Application of the statistical analysis for prediction of the Jordanian GDP by using ARIMA time series and Holts linear trend models for the period （2003-2013）[J]. Mathematical Theory and Modeling， 2014， 4（14）： 19-26.

[15]DINGWeiping， WANG Jiandong， GUAN Zhijin，et al. Cooperative extended rough attribute reduction algorithm based on improved PSO[J]. Journal of Systems Engineering and Electronics， 2012， 23（1）： 160-166. DOI： 10.1109/JSEE.2012.00020.

（編辑 赵勉）