无心外圆磨削能耗建模及优化研究

丁 成，张 华，鄢 威

（武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉 430081）

1 引言

无心外圆磨削是机械行业中一种必不可少的加工方法，例如在加工滚柱、柱塞、轴承套圈等时，除端面外，其他表面几乎都采用无心外圆磨削。无心外圆磨削在零件的精加工上应用较多，而磨削工艺参数的合理选取，不仅可以提高零件的加工精度，而且能够使废品率和生产成本也相应减少[1]。磨削工艺参数的优化问题需要在符合产品技术要求（如表面粗糙度）和磨削加工条件（机床电动机功率要求范围及允许的最大磨削速度、最大磨削力和磨削深度）等设计约束的条件下来进行讨论，计算出最佳工艺参数（砂轮转速、导轮转速、导轮架进给速度等），从而达到提高经济效益的目的（如以最小能源消耗作为决策目标）[2]。伴随着现代科技行业的高速发展，各类软件平台层出不穷，MATLAB 已成为解决最优化问题所必不可少的工具之一，在优化领域中被广泛运用[3]。其具有的初始参数简单化、少编程工作量及强大的图形处理能力等优点，在无心外圆磨削工艺参数优化问题中也卓有成效[4]。通过分析磨削过程的受力情况来建立无心外圆磨削过程的能耗模型，运用蜜蜂进化型遗传算法并结合MATLAB 实现运算，是一种寻求无心外圆磨削最优工艺参数、减少磨削过程能源消耗的新方法。

2 无心外圆磨削能耗优化模型

2.1 磨削力模型的建立

无心外圆磨削时工件作回转中心不定的运动，工件将自由放置在砂轮与导轮之间，由托板对其起支撑作用，工件在砂轮和导轮的联合作用下做回转运动并被不断削除。降低磨削过程的机床能量消耗，实现资源的合理配置对磨削力分析必不可少。而计算磨削力可选用公式进行推导或者用多次实验的方法来测定，如果采用实验的方法来测定，将会提高能源消耗及工作成本，因此可通过分析磨削过程中磨削力的详细受力情况来建立理论模型[5]。从物理学的角度研究单一磨粒的磨削受力情况，当磨粒开始磨削工件时，工件会产生相应的抵抗力，如图1 所示为磨削过程中工件表面的各项受力情况。不考虑摩擦力的作用，磨削力dFx垂直作用在磨粒表面上，其详细受力情况，如图2 所示。磨削过程中能耗主要受dFx的切向分力dFt影响，结合文献[6]得到切向磨削力的公式为：

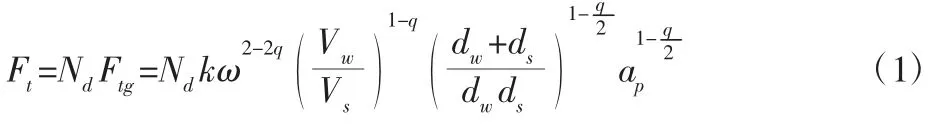
式中：Vw—工件线速度；Vs—砂轮线速度；ag—磨粒磨削深度；ω—磨粒间隔；dw—工件半径；ds—砂轮的半径；ap—砂轮磨磨削深度；k值大小和工件材料有关；q—经验常数，约为0.3。

图1 磨削过程受力分析Fig.1 Force Analysis of Grinding Process

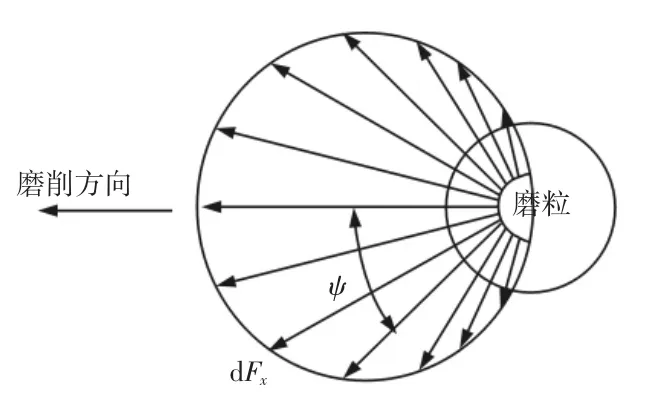
图2 磨粒上的作用力方向Fig.2 Direction of Force on the Abrasive Grain

其中的Nd—动态有效磨刃数，由文献[7]人的计算，对于砂轮与工件的接触弧长ls范围内的动态磨刃数Nd（l）为：

其中，α 和β 的数值大小取决于磨刃形状及磨粒分布情况，一般情况下：0＜α＜2/3，1/3＜β＜2/3。

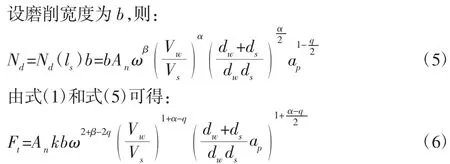
2.2 优化变量及目标函数

（1）优化变量的确定无心外圆磨削过程中，能耗主要受砂轮线速度Vs，工件线速度Vw，导轮架进给速度Vc的影响。假设磨削深度为定值，砂轮线速度Vs越大，尽管磨削力小，但是功率和能耗变大；工件线速度Vw越大，磨削力越大，能耗越大；导轮架进给速度Vc大小随着导轮线速度的变化而变化，因此将该磨削三要素作为优化决策变量。

（2）优化目标的确定主要从能量消耗的角度对参数进行优化，磨削时的功率：

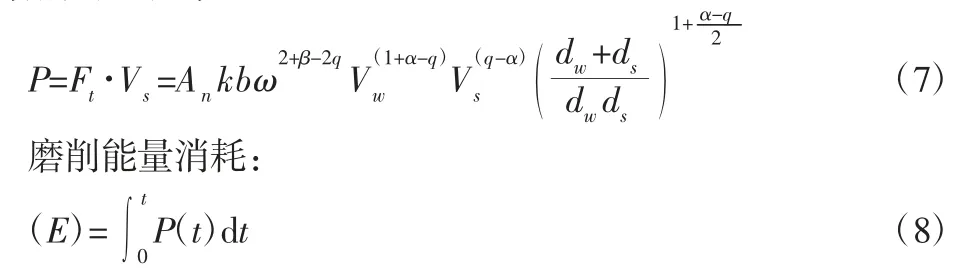
式中：t—磨削的时间，因此将式（8）作为无心外圆磨削过程能耗的目标函数。

2.3 约束条件

磨削加工过程中，决策变量应满足各种加工条件限制，根据磨削加工的实际，选取机床功率约束、表面粗糙度、磨削用量约束作为约束条件：

（1）考虑效率系数η 后，机床功率约束为[6]：

式中：Pmax—机床额定功率，η 一般取0.85。

（2）相对比其他加工方式，磨削属于比较精密的加工工艺，在工件表面粗糙度的要求上会更高。查阅磨削加工手册，平均表面粗糙度的经典值是（0.15～2.5）μm[8]，为了方便测量，在此选定为2μm，所以外圆磨削表面粗糙度约束应为：

（3）磨削用量的约束包括砂轮转速Vs、导轮转速Vw、导轮架进给速度Vc[9]。分别需满足约束式：Vsmin≤Vs≤Vsmax，Vwmin≤Vw≤Vwmax，Vcmin≤Vc≤Vcmax。

综上分析，无心外圆磨削的能耗优化模型如下：

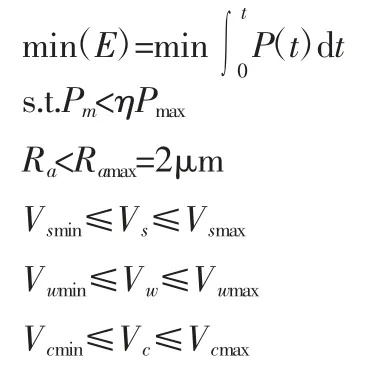
3 改进的蜜蜂进化型遗传算法

3.1 算法简介

传统的简单遗传算法（SGA）存在着效率低、精度差和计算复杂等问题，在许多情况下不是十分有效，它是通过随机搜索进行运算，浪费了不必要的运行时间，局部寻优能力比较差。为了避免以上缺点，在遗传算法的基础上进行改进得到了一种新的蜜蜂进化型遗传算法，该算法从蜜蜂的繁殖进化过程中获得启示：每个蜂群都有一个最优个体蜂王，其与一般的雄蜂个体以给定概率进行交叉和变异操作，为了开辟算法的多样性，引进随机种群参与到子代的进化过程中，使算法的勘探能力大大提升。因为蜂王是种群的最优个体且每一步都存在，算法搜索最优信息的能力大大提高，所以能够保证在收敛速度上有显著的提升，又因为在进化过程中有随机种群的加入，提高了算法结果的精准程度，排除了算法陷入局部最优的缺点。

3.2 算法步骤

蜜蜂进化型遗传算法的原理步骤如下：

（1）将算法的各种参数进行初始化操作，包括种群大小、种群规模参数χ、交叉概率、变异概率、迭代次数，设此时的进化代数为0。（2）首先生成一个初始种群A（t），种群总数量为N，设定种群规模数量。将蜂王Queen 标记为最优适应个体，剩下的作为一般雄蜂。（3）执行t=t+1，在上一代种群A（t-1）中用轮盘赌算法选出χN/2 个雄蜂，并随机生成（1-χ）N/2 个一般雄蜂，将二者合并组成新种群。（4）种群最优个体蜂王Queen 与种群A（t）的一般雄蜂进行染色体交叉互换，新的子代种群为B（t）。（5）将新的子代种群进行染色体变异操作并标记新种群C（t）中最优适应的个体为Queen’。（6）将Queen’与Queen 进行对比，若Queen’的适应度优于Queen，令Queen=Queen’，并且将C（t）替代为种群A（t）；否则Queen 将代替C（t）中适应度最差的个体而得到新的种群A（t）。（7）最后检测是否符合停止运算的条件，若符合，停止运算并输出运算结果；不符合则重回（3）。改进的蜜蜂进化型遗传算法的运行流程，如图3 所示。

图3 改进的蜜蜂进化型遗传算法Fig.3 Improved Bee Evolutionary Genetic Algorithm

选择算子：目的是用相应选择算法来筛选出父代个体中符合条件的子代。而轮盘赌选择算法是将一个轮盘按比例分成多个扇面，每个扇面都代表种群的一个个体，扇面面积的大小正好体现出该个体的适应程度，面积越大，适应度越高，面积越少则适应度越差。适应度的大小决定了遗传概率的大小，概率越高则越容易在遗传环境中生存下来，概率低的则容易在自然法则下淘汰，此方法非常符合自然界中“优胜劣汰，适者生存”的定律，因此将轮盘赌作为选择算法。

交叉概率：交叉概率的典型值大小一般为（0.4～0.99）。在此选择交叉概率为0.6 来防止后代种群出现大范围发散现象。

变异概率：变异概率的大小能够显著影响算法的收敛速度和结果的精确度。如果变异概率大，种群在进化时能够产生更多样的新个体，增加了求解的多样化，但是同时也意味着更低的收敛速度。变异概率小，进化时显得更加单一，种群中新个体减少，解的搜索范围变小，弱化了解的准确度，但相应的收敛速度会有很大提升。变异概率的典型值大小一般为（0.0001～0.1），在此取0.01 保证解的精确度。

停止条件设定为进化代数，此处选取最终迭代数为200。

4 案例研究

软件MATLAB 拥有较强大的运算能力、图形处理、交互式功能以及开放的编程环境。它所自带的工具箱中也各类实用优化算法和功能模块，可以用来解决约束非线性、无约束非线性极值、非线性系统方程等各类复杂的优化求值问题，为工程技术人员带来了极大的便利[10]。为了验证蜜蜂进化型遗传算法的有效性，必须利用MATLAB 软件编制相应的M 文件，然后在计算机上调试运行来求得最优解。

为了让进化过程的收敛速度能够更好的对比显示，我们分别用两种遗传算法对能耗模型进行500 次实验，比较如图4 所示，图中可以看出，蜜蜂进化型遗传算法相较于传统的遗传算法在收敛速度上有明显提升，可以在50 代以内求出最优解。而传统简单遗传算法却在接近150 次的时候才达到近似最优解。

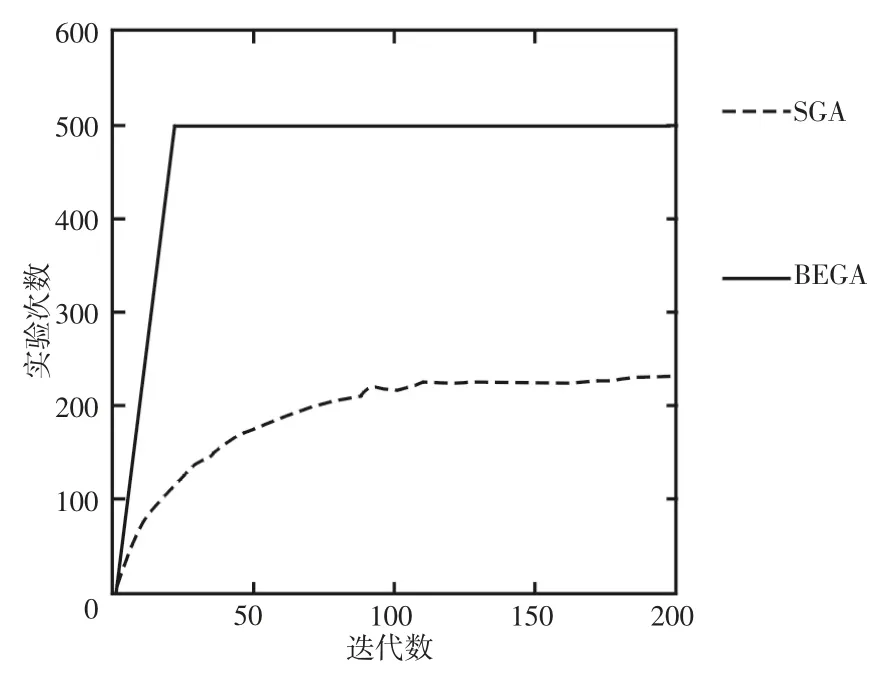
图4 收敛速度对比Fig.4 Comparison of Convergence Speed

为了验证由蜜蜂进化型遗传算法得到的最优解的合理性，有必要将结果与传统的简单遗传算法求得的结果进行分析比较，在MG1050 无心磨床对（20×50）mm 的45#钢圆柱件进行磨削加工，磨削深度选定为0.15mm，磨削时间为30s。能耗优化结果对比如表1 所示，可以看出在使用蜜蜂进化型遗传算法优化过的参数进行加工时，比遗传算法优化的参数进行加工所消耗的能量要减少58J。

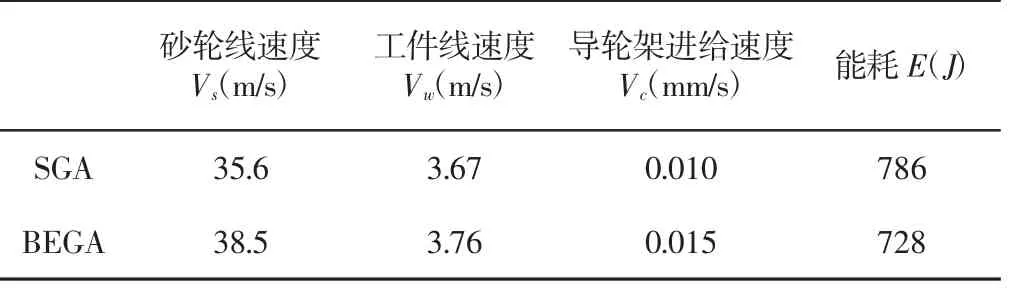
表1 能耗优化结果对比Tab.1 Comparison of Energy Consumption Optimization Results

5 结论

通过分析无心外圆磨削过程的受力情况建立磨削力的模型，在考虑了机床性能和加工约束条件的基础上建立了以能耗为目标的数学优化模型。并运用MATLAB 软件分别结合蜜蜂进化型遗传算法和传统简单遗传算法进行最优值求解，将所得砂轮转速、导轮转速和导轮架进给速度进行实验对比分析，确认蜜蜂进化型遗传算法相比传统的遗传算法在收敛速度和结果精度上更具有优势，能够实现降低能源消耗的目的。