基于workbench 平台的涡旋压缩机涡旋齿瞬态流固耦合分析
2021-04-30冯治国苏亚锋廖飞龙
吴 臻,冯治国,苏亚锋,廖飞龙
(1.贵州大学机械工程学院,贵州 贵阳 550025;2.贵州省特色装备及制造技术重点实验室,贵州 贵阳 550025;3.贵州量子动力科技有限公司,贵州 贵安 550003)
1 引言
涡旋压缩机工作过程中涡旋齿的受力变形受流场分布的影响极大,很多学者尝试通过试验的方式来得到涡旋压缩机的内部流动情况及涡旋齿受力变形[1-3]。但是压缩机封闭的工作腔、内部流场边界的移动和小的间隙,使得任意曲轴转角下内部流场信息的变化情况及涡旋齿的变形规律很难方便准确地得到,采用数值模拟方法获得压缩机工作过程中流场的分布与涡旋齿的受力变形已成为涡旋压缩机热点方向之一。文献[4-6]建立了涡盘的数值模拟模型,把涡旋齿简化为悬臂梁使用理想绝热过程进行校核。文献[7]将涡旋齿面的压力载荷简化为线性分布,对涡旋齿进行了受力分析。文献[8]根据流场模拟的结果,在涡旋齿上将模拟得到的压力分段施加,计算的准确性在一定程度上得到提高。由于涡旋压缩机运转过程中动盘位置不断变化,在不同曲轴转角处涡旋齿的所受的流体压力是不同的。现有文献中在涡旋齿面上加载压力时都进行了较大的简化,这些简化加载方式均不能很好地与实际情况贴合。文献[9-14]对速度式流体机械进行了流固耦合研究。
Ansys workbench 平台是一个高度集成化的CAE 分析系统,其中包含流场,固体场,电磁场等多个分析模块,在workbench 大环境下各个模块之间能够顺利的进行数据交换。针对容积式的涡旋压缩机涡旋齿上压力载荷难以准确加载的问题,在workbench平台下结合fluent、Transient Structure 以及cfd-post 三个模块,首先在fluent 中对涡旋压缩机内部流动进行模拟,得到任一曲轴转角下流场边界的压力载荷分布,然后通过cfd-post 导出边界压力数据,在Transient Structure 中将流场边界压力加载到与之对应的涡旋齿面上,通过这样的方式实现涡旋压缩机涡旋齿的瞬态流固耦合,进而对涡旋齿进行受力变形分析,得到涡旋齿的变形与应力分布规律,该计算结果能更准确的反映涡旋齿受不断变化的流场力的影响。
2 控制方程
涡旋压缩机运行过程中内部流体满足质量和动量守恒方程:

式中:τgτs—气体与固体表面应力;n—分界面处公法线矢量;rgrs—气体与固体边界的位移。
3 流场分布与数据传递
3.1 物理模型
涡旋压缩机是通过工作腔容积的变化来完成对气体的压缩的机械。涡旋压缩机工作腔的轴向投影,如图1 所示。

图1 涡旋压缩机工作腔Fig.1 Working Chamber of Scroll Compressor
当曲轴转动带动盘绕静盘中心作公转平动时,工作腔容积相应地缩小扩大,完成气体的吸入、压缩和排气。气体从入口进入经压缩后由静盘中心处的出口排出。
3.2 网格划分
由于需要对涡旋齿进行流固耦合分析,现将涡旋齿与其所构成的流体域合在一起进行网格划分,且使涡旋齿与流体分界面处网格节点一一对应以使流体域与固体域之间的数据传递顺利进行。动盘绕中心作公转平动,压缩机流场的边界是不断变化的。流场边界运动时,网格会发生变形,由于三角形相对于四边形对于变形的适应性较好,为了防止网格变形中网格出现负体积,结合流场各部分在几何上所具有的沿一方向扫掠成型的特点,以各部分端面面网格为三角形进行拉伸得到流场网格,网格数372034,节点数1188217,如图2 所示。

图2 网格划分Fig.2 Mesh Generation
3.3 边界条件与流固界面映射
所研究压缩机的涡旋盘型线为圆渐开线,基本设计参数:基圆半径2.6mm,渐开线起始角0.7rad,涡旋齿高20mm,齿厚3.5mm。涡旋压缩机的边界条件为入口压力0.25MPa,出口压力1.45MPa,转速7200r/min。非定常流动,由于动盘是作旋转平动,流动会产生涡流,湍流模型选取RNGk-ε 模型,相对于其他模型RNGk-ε 模型针对高雷诺数的湍流流动,能够更好地识别不同尺度的湍流涡流。流动区域的动网格采用弹簧光顺法与2.5D重构法相结合。
在进行流场分析时作为固体场的涡盘与流体域一同进入fluent,在fluent 中被划分为固体域与流体域。同时将流体域与固体域在它们的分界面处进行耦合以实现流场数据到固体场的映射,为后续数据传递作准备。
3.4 流场分布
在workbench 平台下的fluent 模块中完成对流场的分析。主轴在不同时刻时压缩机内的压力场分布,如图3 所示。
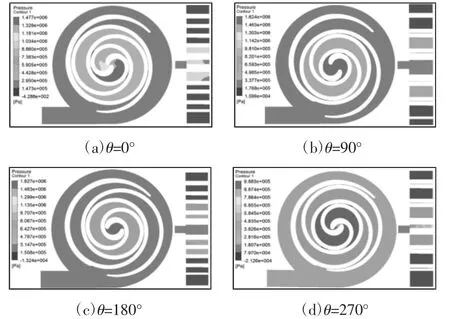
图3 流场分布Fig.3 Flow Field Distribution
压力分布整体呈中心对称,各腔压力在端面上分布基本均匀且越靠近涡旋中心,腔内压力越高。在齿高方向取不同转角时中心工作腔内的20 个特征点,其压力值,如图4 所示。

图4 齿高方向压力分布Fig.4 Pressure Distribution in Tooth Height Direction
工作腔内压力分布沿齿高方向不均匀,最大有32%的压力变化,因而三维流场能更准确的反映流场的实际分布情况。涡旋齿的受力特性受压力分布的影响,曲轴转角90°时取动盘齿顶沿齿头到齿尾内外侧型线上的45 个特征点,提取各点压力值并取内外两侧对应点之差,如图5 所示。
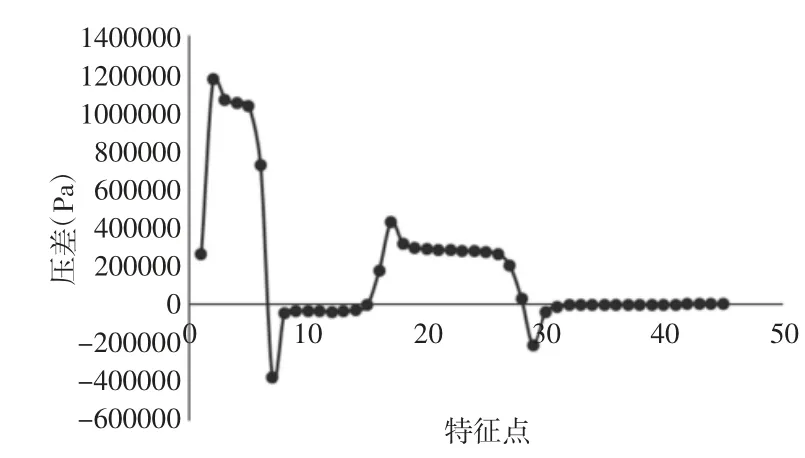
图5 齿顶内外侧压差Fig.5 Pressure Difference Between Inside and Outside of Tooth Top
从图可看出齿头附近压差较大,齿尾压差较小,由齿头到齿尾压差逐渐减小。
4 涡旋盘的有限元分析
4.1 流固界面数据传递
流固耦合中流体域与固体域的数据的传递是关键的一步,在fluent 中完成流场分析后通过cfd-post 将流动边界压力随时间变化的数据导出到Transient Structure 模块,通过插值运算映射到涡旋齿耦合面上,从而实现完整的数据交换。由于涡旋齿的压力载荷来源于三维流场,使得涡旋齿所受气体力随着曲轴转动与流场边界压力同步变化,更加贴近于实际情况。流固界面数据传递,如图6 所示。
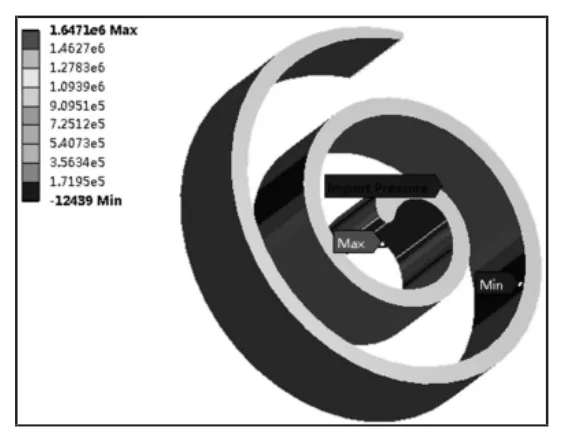
图6 流固界面数据传递Fig.6 Fluid-Solid Interface Data Transfer
4.2 涡旋盘的约束条件
涡旋压缩机工作运行中,动盘绕转动中心做公转平动其本身不会自转,其约束为限制涡旋齿z轴方向的移动自由度与绕z轴转动的自由度。
4.3 涡旋齿的受力变形
涡旋盘的材料为4030-T6 铝材,基本参数:弹性模量7.90E+10 N/m^2,泊松比0.340,密度2.68E+03 kg/m^3。
不同转角下涡旋齿的应力与变形情况,如图7、图8 所示。随着曲轴转角的不同涡旋齿的变形形式、最大变形量、最大应力也不同。涡旋齿的变形主要发生在齿头到压缩腔一段,齿尾变形相对较小。涡旋齿的最大应力主要在齿头根部以及压缩腔一段的根部。

图7 不同转角下涡旋齿变形Fig.7 Deformation of Scroll Teeth at Different Angles of Rotation

图8 不同转角下涡旋齿应力Fig.8 Stress of Scroll Teeth at Different Angles of Rotation
一个周期内涡旋齿的平均变形与平均应力的变化情况,如图9、图10 所示。

图9 涡旋齿平均变形Fig.9 Average Deformation of Scroll Teeth
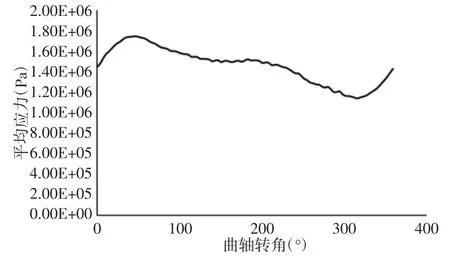
图10 涡旋齿平均应力Fig.10 Average Stress of Scroll Teeth
可以发现涡旋齿的平均变形与应力均在曲轴转角为46.8°时达到最大。其变形与应力云图,如图7(b)、图8(b)所示。
在涡盘齿根处由齿头到齿尾的内外侧轮廓上选取60 个特征点,得到应力从齿头到齿尾方向上的分布规律,如图11 所示。可以看出无论是内侧还是外侧应力变化都是靠近齿头高,靠近齿尾低。内侧最大应力值与最小应力值相差63 倍,而外侧相差43倍。
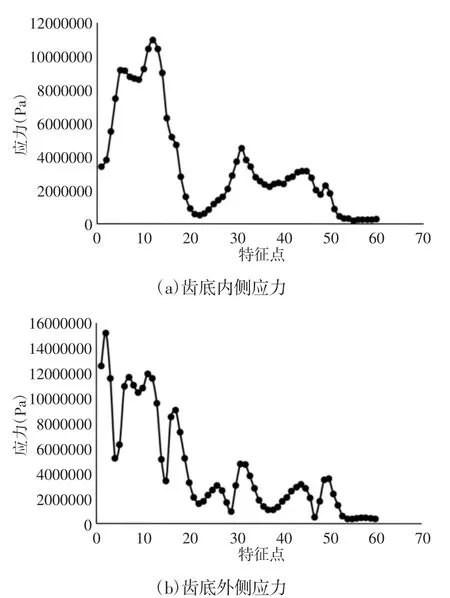
图11 涡旋齿底应力分布Fig.11 Stress Distribution at the Bottom of Scroll Teeth
涡旋齿在内外两侧的压力作用下发生变形。在涡盘齿顶内外侧轮廓上取60 个特征点,得了其变形从齿头到齿尾的分布曲线,如图12 所示。
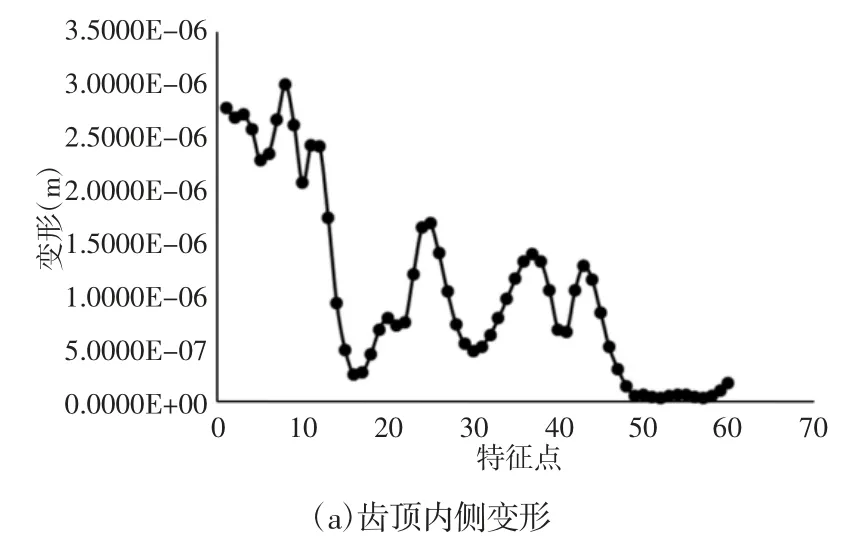

图12 涡旋齿顶变形分布Fig.12 Distribution of Scroll Top Deformation
可以看出沿着涡旋型线的方向在涡旋型线展角175°和265°附近有3 处变形的峰值。涡齿两侧的压力差使该段涡旋齿发生相对严重的变形。齿顶内侧边界中,最大与最小变形相差89 倍,而齿顶外侧边界中,其值相差74 倍。涡旋齿的最大应力与变形随曲轴转角的变化情况,如图13、图14 所示。在转角为180°时,涡旋齿的最大变形与应力达到最大。涡旋齿在气体压力作用下的变形与应力云图,如图7(c)、图8(c)所示。该状态涡旋盘应力与变形分布很集中,应力主要集中在齿头根部附近,变形主要集中在齿头顶部附近,其余部分应力与变形相对较小。
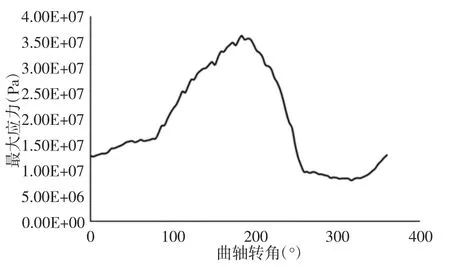
图13 涡旋齿最大应力分布Fig.13 Maximum Stress Distribution of Scroll Teeth
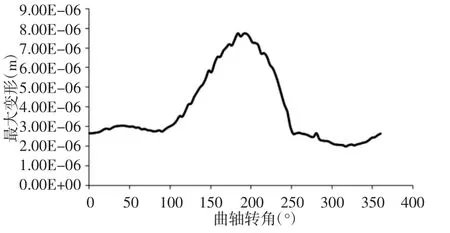
图14 涡旋齿最大变形分布Fig.14 Distribution of Maximum Deformation of Scroll Teeth
涡盘分析的最大变形为7.45e-7m,所用动静盘啮合间隙为0.05mm,涡盘变形远小于啮合间隙,涡盘分析的最大应力为3.55e7Pa 远小于涡盘材料4032-T6 的强度极限3.15e8Pa。故涡旋压缩机的涡旋齿在该气体载荷作用下能够正常工作。
5 结果对比
文献[4-6、8]中针对涡旋压缩机的涡旋齿进行了受力变形分析,其最大应力与最大变形均出现在涡旋齿齿头处,与分析结果相符,由于涡盘材料以及边界条件的差异其具体的最大应力值与最小应力值不同。使用瞬态流固耦合的计算方法,更能充分反映变化的流场对涡旋齿受力的影响,模拟结果与实际情况更加贴近。
6 结论
(1)基于workbench 平台提出了一种瞬态流固耦合的模拟方法,该方法对于涡盘表面的压力施加最接近于实际情况,对于任意曲轴转角时涡旋齿的受力变形分布均可得到。涡旋齿的最大应力和变形均发生在涡旋齿头部。该方法不但适用于涡旋压缩机,也适用于其他容积式压缩机。(2)涡旋压缩机的三维压力场分布,压力分布整体呈中心对称,各腔压力分布在端面上基本均匀且越靠近涡旋中心,腔内压力越高。在齿高方向压力分布不均匀,最大有32%的压力差异。结果表明90°时动盘齿顶内外侧型由齿头到齿尾压差压差逐渐减小。(3)得到了涡旋齿的受力和变形规律,涡旋齿在压差的作用下其应力和变形由齿头部到尾部逐渐减小。各转角下涡旋齿的最大应力发生在齿根处,而最大变形发生在齿顶。
