基于电机电流经验模态分解的行星轮故障诊断
2021-04-30门兰城庞新宇刘利平
门兰城,庞新宇,李 峰,刘利平
(1.太原理工大学机械与运载工程学院,山西 太原 030024;2.阳煤集团,山西 阳泉 045000)
1 引言
行星齿轮箱是许多行星齿轮围绕太阳轮旋转的传动系统,它也是一种降低转速和增加扭矩的传动系统。适用于高速大功率以及低速大转矩的机械传动。在运转过程当中,行星齿轮箱时常承受复杂的动态重载,较容易发生机械故障[1]。而在行星齿轮箱中,行星轮作为行星轮系运转的关键部件,同时与太阳轮和齿圈啮合,出现故障的概率更高。近些年来,针对行星轮故障诊断的研究取得了一定的进展。文献[2]针对经验模态分解(EMD)过程中的模态混叠问题,提出了将EMD 和小波包分解(WPD)相结合的颤振识别方法。文献[3]基于小波方法提出了约束自适应算法检测行星齿轮机构的齿轮损伤。文献[4]考虑了关键部件损伤程度的行星轮系模型,为行星齿轮传动的初期故障诊断提供了支持。文献[5]建立了行星齿轮箱局部故障振动信号模型,并应用频谱分析法对行星轮故障进行了诊断。文献[6]提出集合经验模态分解(EEMD)进行齿轮箱降噪及故障特征提取方法。文献[7]提出一种单分量个数的估算方法,应用于行星齿轮箱振动信号分析中,验证了该方法的有效性。这些方法都是基于振动信号的诊断方法。但是振动信号具有受噪声干扰大,信号混叠严重,传感器价格高等缺点。而电流信号具有方便监测,不受噪声干扰,包含传动信息多等优点。因此近些年一些研究者将电机电流信号分析作为机械故障诊断的方法。但是由于行星齿轮传动的复杂性以及电流工频的影响,普通的频谱分析,无法从电机电流信号中有效的识别出行星轮故障,因此提出一种基于电机电流经验模态分解(EMD)的故障诊断方法,并通过实验分析证明了该方法的有效性。
2 基于电流信号EMD 分解的行星轮故障诊断
当电动机的齿轮箱齿轮失效时,它会引起扭转振动信号的变化[8]。电机的气隙转矩会随着齿轮的扭转振动而周期性地变化,这将导致定子磁链改变,这最终会导致定子电流的规则变化。电磁转矩的波动反映在相电流的幅度调制中,并且转速的波动表示为相位调制。
2.1 行星轮故障状态时电流特征
当齿轮运行状况良好时,由于齿轮运行特性的影响,负载电机的扭矩TL是由恒定转矩T0和频率为fr1,fr2,fm,相位为φr1,φr2,φm,的波动转矩组成[9],即:

式中:fr1—输入端信号转频;fr2—输出端信号转频;fm—啮合频率。
由前面的分析可知,在电流信号频谱中会出现fe±fr1、fe±fr2、fm±fe的频率成分。当齿轮发生局部故障时,每次故障齿啮合时,负载转矩都会产生脉冲冲击。只有一个轮齿发生故障时,故障将会在原扭矩TL中引入频率为故障齿轮转频fr的周期性脉冲f(t),对f(t)进行傅立叶变换得到:

2.2 行星齿轮故障特征频率
与定轴齿轮箱不同,行星齿轮箱齿轮的故障特征频率不仅取决于每个齿轮的转动频率,还取决于齿轮箱的特定结构参数。对于行星齿轮系中的行星齿轮局部故障,当故障点与太阳齿轮和齿圈啮合时,将发生冲击现象。行星轮局部故障特征频率表达式为[5]:

2.3 电流信号EMD 分解过程
经验模态分解(EMD)是美国NASA 的HuangE 等在1998年提出的一种自适应时频处理方法,适用于非线性及非平稳信号的分析,EMD 把信号分解成有限个本征模态函数(IMF)[10]。该方法基于数据本身的时标特征来分解信号,而没有任何预先设定的函数。由于这种特性,EMD 方法理论上可以应用于任何类型信号的分解。
电流信号分析处理简要过程如下:先将采集的电机原始电流信号导入matlab 中,再通过EMD 将电流信号分解成有限个IMF 分量,然后选取有效的IMF 分量做傅立叶变换得到频谱图,最后通过对行星轮缺齿故障与完好状态下的IMF 分量频谱图进行对比分析,从而实现行星轮缺齿故障的有效诊断。流程图,如图1 所示。
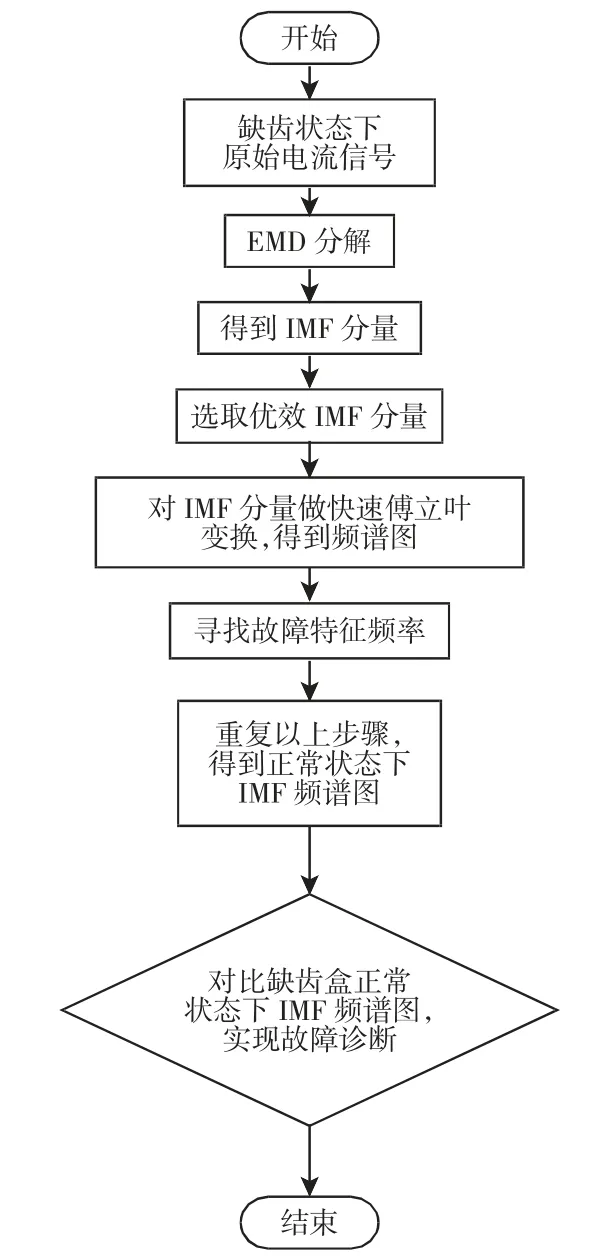
图1 故障诊断流程图Fig.1 Fault Diagnosis Flow Chart
3 实验分析
3.1 试验装置简介

表1 各齿轮齿数Tab.1 Tooth Number of Gears

图2 试验台Fig.2 Testbed
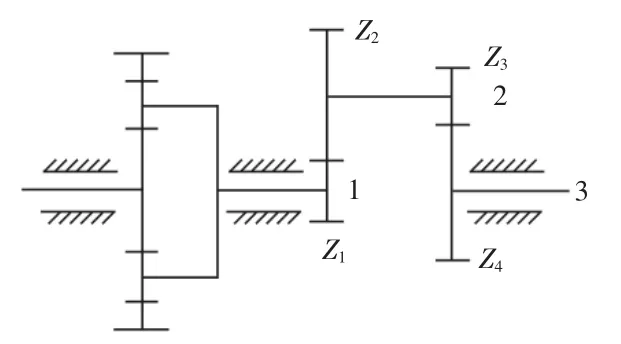
图3 传动系统示意图Fig.3 Schematic Diagram of Transmission System
行星齿轮箱故障模拟试验台是由变频器、驱动电机、行星齿轮箱、平行轴齿轮箱、磁粉制动器等设备组成,电机输出端通过联轴器直接与太阳轮相接。该行星齿轮箱有1 个太阳轮,4 个行星轮,齿圈与箱体固定。该试验装置可以模拟太阳轮、行星轮、平行轴齿轮等齿轮的缺齿故障,通过分别采集故障齿轮和完好齿轮两种状态下的电流信号,进行分析处理对比,来实现故障诊断。其中行星齿轮的减速比为4.571,为第一级减速装置;平行轴齿轮箱(定轴轮系)为第二/三级减速装置。齿轮箱各齿轮参数,如表1 所示。试验台,如图2 所示。齿轮传动系统示意图,如图3 所示。实验所用完好和缺齿行星轮,如图4 所示。电流传感器,如图5 所示。

图4 完好和缺齿行星轮Fig.4 Normal and Faulted Geas

图5 电流传感器Fig.5 Current Sensor
3.2 实验过程
选取电机电流工频fe=50Hz,电机输出端转速为3000r/min,分别采集行星轮完好和故障状态下电流信号。由于太阳轮直接和电机输出端转轴相接,因此太阳轮转频fS=fe=50Hz;根据齿轮箱参数计算可得行星架转频fc=fS/4.571=10.9Hz,齿轮副啮合频fm=1093.9Hz,行星轮故障特征频率fp=30.4Hz。
3.2.1 电流信号时域和频谱对比分析
行星轮完好和故障状态下电流信号的时域和频谱,如图6、图7 所示。
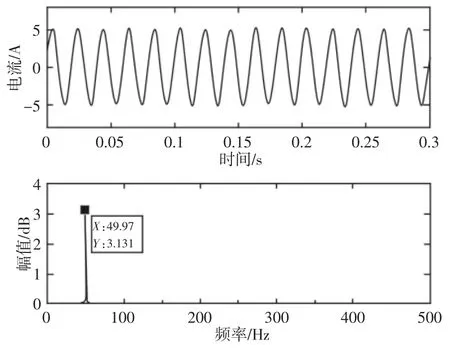
图6 完好状态时域和频谱Fig.6 Time Domain and Spectrum of Normal
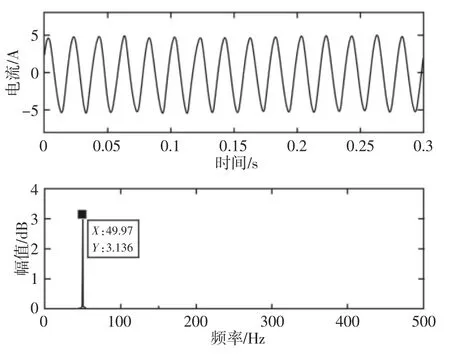
图7 故障状态时域和频谱Fig.7 Time Domain and Spectrum of Fault
对比图6 和图7 可知,两种状态时电流信号的时域图均接近于正弦波;在频谱图中电流工频fe=50Hz 均占据主要成分,其他频率成分不明显。由此可见,直接对电流信号进行频谱分析无法找到故障频率,不能实现行星轮故障的有效诊断。
3.2.2 电流信号有效IMF 分量的频谱对比分析
进一步对完好和故障状态下电流信号进行EMD 分解,信号从高频到低频被分解成了不同频率段的信号成份。由于前四层包含的频率信息比较多,这里重点对电流信号的前四层做对比分析。完好状态下电流信号有效IMF1~IMF4 分量,如图8 所示。
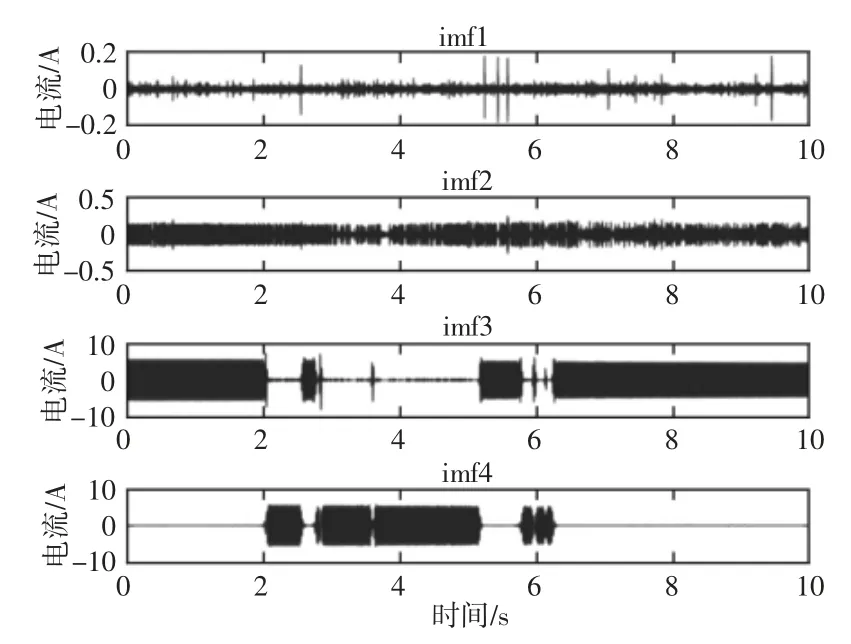
图8 完好IMF1~IMF4 分量Fig.8 IMF1~IMF4 Components of Normal
故障状态下电流信号有效IMF1~IMF4 分量,如图9 所示。
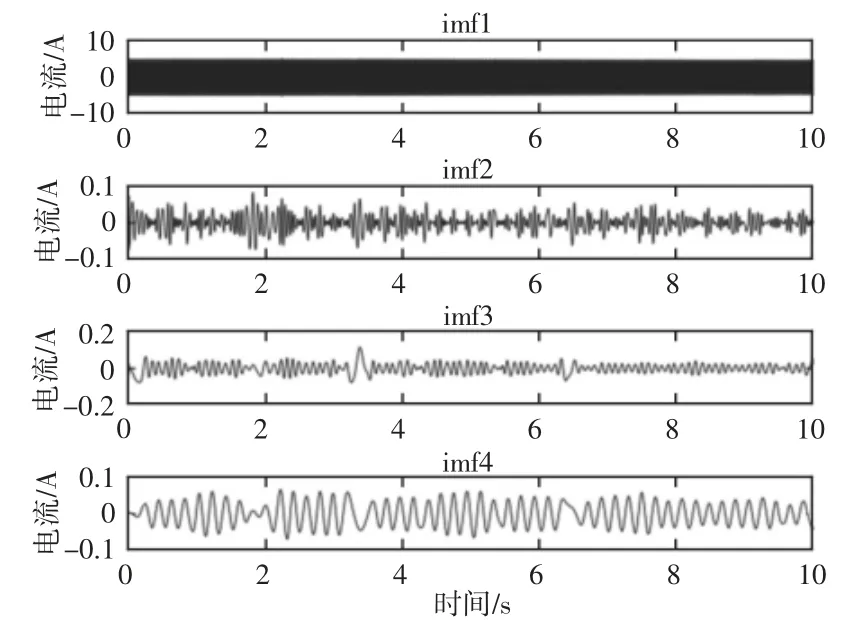
图9 故障IMF1~IMF4 分量Fig.9 IMF1~IMF4 Components of Fault
分别对两种状态IMF1~IMF4 分量做傅立叶变换得到对应频谱,如图10、图11 所示。
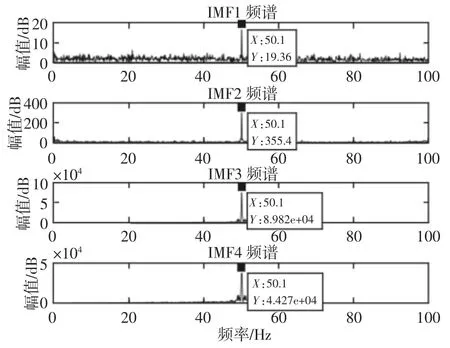
图10 完好IMF1~IMF4 频谱Fig.10 IMF1~IMF4 Spectrogram of Normal
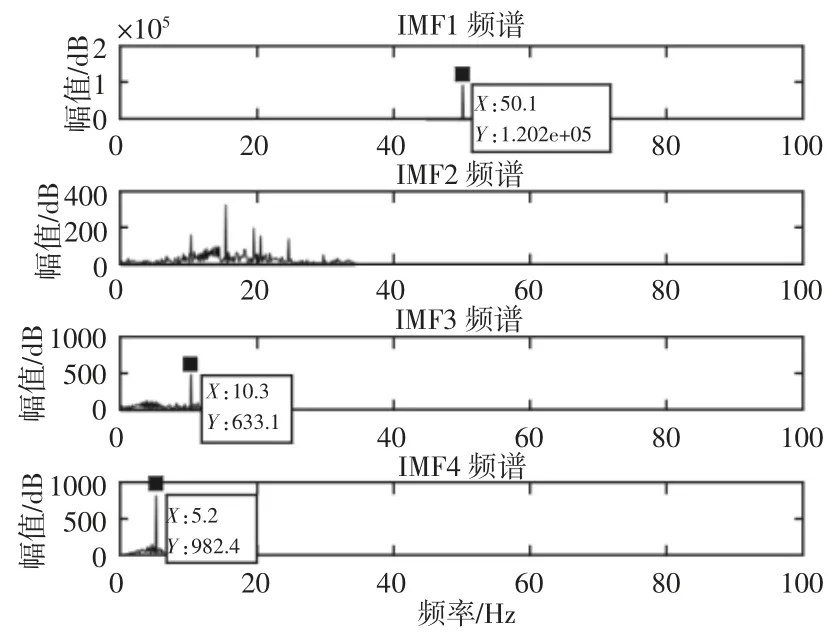
图11 故障IMF1~IMF4 频谱Fig.11 IMF1~IMF4 Spectrogram of Fault
由图10 可知,完好状态IMF1~IMF4 分量频谱图中只有明显的电流工频fe=50Hz 占据主要成份,无故障特征频率存在,故不需要做具体分析。
由图11 可知,故障状态IMF1~IMF4 分量频谱中频率信息比较丰富,IMF1 频谱中以电流工频fe=50Hz 为主,不再做具体分析。IMF2、IMF3、IMF4 频谱中频率信息丰富,着重分析。为了方便观察分析,对故障状态IMF2 分量频谱进行局部(0~40)Hz 放大,如图12 所示。

图12 故障IMF2(0~40)Hz 频谱Fig.12 IMF2(0~40)Hz Spectrogram of Fault
由图11 可知,IMF3 分量频谱中,在10.3Hz 有明显的冲击峰值,为fc。IMF4 分量频谱中,在5.2Hz 处有明显的冲击峰值,为0.5fc。
由图12 可知,IMF2(0~40)Hz 分量频谱中,在10.3Hz 有明显的冲击峰值,为行星架转频fc;在15.4Hz 有明显的冲击峰值,为0.5fp;在19.5Hz 处有明显的冲击峰值,为fe-fp;在20.5Hz 处有明显的冲击峰值,为2fc;在24.6Hz 处有明显的冲击峰值,为fe-fp-0.5fc;在29.7Hz 处有明显的冲击峰值,为fp。
由于行星齿轮的缺齿故障,导致在行星架旋转过程中出现载荷不均衡的情况,体现在故障电流信号的频谱中为转频或倍频处有冲击峰值。

4 结论
通过对行星轮缺齿故障时电机定子电流理论模型分析,以及实验验证,可以得出以下结论:(1)当行星轮缺齿故障发生时,EMD 方法可以有效的将定子电流信号中的基频和故障特征频率分开,有效的去除了电流信号中基频的干扰。(2)通过选取合适的IMF 分量,经傅立叶变换求其频谱,可以有效的提取出故障特征频率。为行星齿轮箱故障诊断提供了一种新的思路。(3)针对本论文实验中所出现的信号混叠现象,并未考虑其对实验结果的影响,在以后的研究中可以参考文献[2]中提到的,通过EMD 分解和小波包分解(WPD)结合的方法来进行故障诊断。
